Hierarchiczne struktury danych na przykładzie sieci drenażu

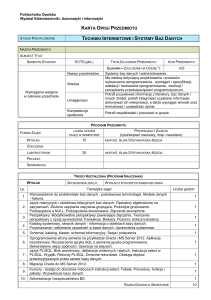
Hierarchiczne struktury danych na przykładzie
sieci drenażu
Przykład danych hierarchicznych
Sieć drenażu: struktura
hierarchiczna
Topologia sieci drenażu
Model terenu: punkt wyjścia
Sposoby otrzymywania sieci
drenażu
Sieć drenażu: efekt analizy
Podział na subzlewnie
Wektoryzacja sieci
Organizacja danych modelu
topologicznym
node = 1
n_lines = 3
xy = 616198.592392 392909.117460
node = 2
n_lines = 3
xy = 680335.950885 443081.083377
node = 3
n_lines = 1
xy = 632750.168778 427563.980516
node = 4
n_lines = 1
xy = 660680.953928 398598.721842
NODES
nr
n_lines
GEOM
coordinates
LINES
Nr
From_node
To_node
Left_area
Right_area
GEOM
bounding box
AREAS
nr
n_lines
centeroid
GEOM
bounding box
Wbudowana topologia
node = 99, n_lines = 3, xy = 3792362.500000, 5606587.500000
line = -112, type = 2, angle = -0.785398
line = -96, type = 2, angle = 0.785398
line = 104, type = 2, angle = 2.356194
Modele hierarchiczne w języku
SQL

Standard SQL nie obsługuje hierarchii

Modele hierarchiczne poza standardem SQL:

model sąsiedztwa

model materializowanej ścieżki
Model sąsiedztwa


bardzo prosta topologia:

każdy „potomek” zna swojego „przodka”

każdy „przodek” może mieć wiele „potomków”

każdy „potomek” ma jednego i tylko jednego „rodzica”
Obsługa takiej topologii przez język SQL wymaga zastosowania
funkcji rekursywnych lub specjalnych klauzul, które nie są
dostępne w większości systemów bazodanowych
1
4
3
7
2
9
5
6
8
10
11
3-1
2-1
5-1
7-3
...
11-9
TauDEM topology
Budowanie prostej topologii
Model materializowanej ścieżki

Bardziej złożona topologia

każdy potomek zna łańcuch wszystkich swoich rodziców aż do najstarszego

zapis hierarchii wygląda następująco:
5:2:1


Łańcuch może być dowolnej długości
Taka topologia może być obsługiwana przez standardowe
zapytania SQL lub z użyciem specjalizowanych narzędzi (ltree)
1
4
3
11:9:7:3:1
7
2
9
5
6
8
10
11
Próbkowanie różnych danych
rastrowych: graf
Efekty zapytań SQL