Równanie Schrödingera Równanie Schrödingera Od 1 atomu (gaz

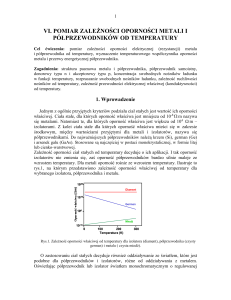
Równanie Schrödingera
−
2
 ∂ 2ψ ∂ 2ψ ∂ 2ψ

+
+
8π m  ∂x 2 ∂y 2 ∂z 2
h
2
Równanie Schrödingera

 + V (r )ψ = ωψ

jest podstawowym narzędziem mechaniki kwantowej.
Komplet to równanie Schrödingera na szukane: energię ω
i funkcję falową ψ(r), oraz 5 warunków (stanowiących
integralną część metody) które musi spełnia funkcja
falowa ψ:
(1)ψ ma być funkcją ciągłą, (2)o ciągłych pochodnych,
(3)jednoznaczna, (4)ograniczona i (5)unormowana
gdzie danymi są
•h stała uniwersalna Plancka
•m masa cząstki
•V(r) jej energia potencjalna
i wynikiem obliczeń jest
•{α, ω(α), ψα(r)}, zbiór rozwiązań indeksowanych przez α
(tzw. liczba kwantowa wskazująca stan α) dla energii ω i
funkcji falowej ψ.
1 = ∫ dV ψ
∞
Natomiast informacją wejściową dla RS (które jest
równaniem ruchu jak II zasada dynamiki Newtona) jest
energia potencjalna V(r) (lub siła F jak dla F=ma)
Od 1 atomu (gaz) do wielu
atomów (ciecz, ciało stałe)
Pasma energii: ∆ω << T << W
1 atom
gaz=N atomów
kryształ=N atomów
ω(α)=energia to samo ω(α)
pasmo: 0<ω<W
1 linia, W=0 1 linia wielokrotna N linii, N=1024, W>0
gaz
V(atom)=V(gaz)
Ciało stałe tworzą atomy ułoŜone ciasno, stąd inne V(r) niŜ w
atomie. Wynik to:
1)rozszczepienie=rozrzut poziomów ω, W=1eV=104 K,
stąd ∆ω=W/N=10-20 K, energia NIEMAL ciągła
2)większa szerokość W dla pasm o wyŜszych energiach
3)ciecz Fermiego=widmo niemal ciągłe + zakaz Pauliego
4)energia Fermiego, zamroŜenie czy ruchliwość elektronów
5)przewodniki i izolatory, zachodzenie pasm
ciecz, c. stałe
V(c.stałe)=inne
ZAKAZ Pauliego:
fermiony i bozony
stan układu:
energia:
Od 1 atomu (gaz) do wielu
atomów (ciecz, ciało stałe)
α=(n,l,m,s)
ω(n,l)
Uwaga: np. dla α=(2,1,-1,1/2), β=(2,1,+1,-1/2), pomimo
Ŝe α i β są róŜne, to ω(α)= ω(β) i dlatego zakaz Pauliego
brzmi poprawnie n(α)=0,1 (błędnie ω(α)=0,1).
Gdy zakaz Pauliego:
nie obowiązuje, n(α)=0,1,2,3,...
to bozony
np. fotony
obowiązuje, n(α)=0,1
fermiony
np. elektrony
2
ω
0
...na przykładzie rozkładu n=5 cząstek
FERMIONY
x
energia Fermiego x
stan wzbudzony
x x
BOZONY
...
x x
x
stan wzbudzony
x x
x
stan podstawowy x x
xxxxx x xx
temperatura T
0 T>0
0
T>0
zakaz Pauliego
tak
nie
Zachodzenie pasm
Zachodzenie pasm
- czyli dlaczego magnez jest metalem
Przykł
1s22s2p63s2 (f=2/2)
Przykład: (atom) magnez 12Mg=1s
1s22s2p63s1 (f=1/2=50%) ==> spodziewany metal
11Na=1s
tak 12Mg=1s
1s22s2p63s2 (f=2/2=100%) ==> izolator, ???
pasmo 3p
pasmo 3s
11Na
3s1
pasmo 3s
12Mg
3s2
atomy (gaz)
3p
c. stał
stałe (kryształ
(kryształ)
3s
pasmo 3s
12Mg
3s1,4p0,6
3p
3s
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
11Na=3s
3s1
11Na=3s13s
2
12Mg=3s
3s1,6p0,4
12Mg=3s 3s
Metale, izolatory i półprzewodniki
Mechanizm przewodnictwa σ(T), izolator to σ=0
metal
metal
półprzewodnik
0 ==== 0
- ===> +
T=0
T>0
0
T>0
- ====> +
xx0xxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
x
<== ==>
x0xxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
0
xxx xx
xxxxxx
xxxxxx
xx xxx
xxxxxx
xxxxxx
x
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxxx
Model silnego wiązania, pasma
r
ω (k ) = ω0 − 2 ⋅ [t x cos(k x a x ) + t y cos(k y a ) + t z cos(k z a / 2)]
...jest obliczoną dla tetragonalnej struktury krystalograficznej
energią TBM dla parametrów (tx,ty,tz) bezpośrednio związanych z
odległościami (ax,ay,az) między najbliŜszymi sąsiadami wzdłuŜ
osi krystalograficznych (x,y,z), t ~ a–5. (Wykładnik 5 dla np.
stanów 3d.) Z powyŜszego wzoru wynika szerokość pasma
W=4(tx+ty+tz).
Oczywiście t 0 jest limitem atomowym dla którego
otrzymujemy poziom energii ω=ω0, W=0, zamiast pasma.
Najczęściej dobieramy parametr ω0 tak, aby dno pasma k=0
opowiadało energii ω=0. Wówczas
ω0=2(tx+ty+tz).
Na
Mg
Model silnego wiązania, pasma
Model silnego wiązania (TBM=Tight Binding Model) to b. dobry
przykład dla wyjaśnienia koncepcji pasm. TBM to przybliŜone,
analityczne rozwiązanie dla potencjału V(r) w krysztale, który jest
stosunkowo bliski potencjałowi atomowemu.
Atom (pasmo=poziom, W=0) TBM(pasmo, W>0) model
elektronów swobodnych(pasmo Wnieskończoność).
Idea: periodyczny potencjał V(r) w krysztale zawsze daje energię ω
electronu postaci ω(kx,ky,kz), gdzie kx,ky,kz to tzw. wektor falowy
o dyskretnych wartościach, co czyni energię ω równieŜ dyskretną.
Np. dla 26Fe=3d7.24s0.8, moŜemy stosować TBM dla elektronów 3d.
Dla elektronów walencyjnych 4s, alternatywny model elektronów
swobodnych, V(r)=const, jest bardziej właściwy.
Model silnego wiązania, pasma
Często występuje przypadek małej liczby N elektronów (np.
półprzewodniki) które zatem zajmują niskie poziomy energii
w pobliŜu dna pasma k=0. Dla ilustracji rozpatrzmy np.
tx=ty=tz. Stosując przybliŜenie
cos( x) ≈ 1 − x 2 / 2 → [cos(k x a ) + cos(k y a ) + cos(k z a )] ≈ 3 − k 2 a 2 / 2
mamy
cos( x) ≈ 1 −r x 2 / 2 → [cos(k x a ) + cos(k y a ) + cos(k z a )] ≈ 3 − k 2 a 2 / 2
a stąd ω(k ) ≈ ω0 − Z ⋅ t + t ⋅ k 2a2
Kwadratowa zaleŜność ω(k) jest
r charakterystyczna dla modelu
r
elektronów swobodnych, ω (k ) ≈ V0 + h 2 ⋅ k 2 / 2m, dla V (r ) = V0
Zatem dla modelu TBM moŜemy zidentyfikować tzw. masę
efektywną m*, zamiast parametru t. Np. dla Si: me=0,31m,
mh=0,38m. Pamiętamy a=F/m.