Bohra model atomu

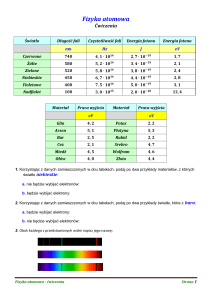
BOHRA MODEL ATOMU + WIDMA
Powtórzyć:
dynamikę (r.p.o.), bryłę sztywną (L), elektrostatykę, fale, dualizm ...
Postulaty:
1. Postulat istnienia stanów stacjonarnych – istnieją stany stacjonarne atomu, w których nie
emituje on energii i stanom tym odpowiadają określone orbity elektronów, krążąc po których
nie emitują one energii.
2. Postulat kwantowania orbit – moment pędu elektronów atomu, znajdującego się w stanie
stacjonarnym jest skwantowany w myśl reguły:
=
3. Postulat częstości – podczas przechodzenia atomu z jednego stanu stacjonarnego do innego
zostaje pochłonięty, lub wyemitowany kwant energii (porcja energii) określony(a) wzorem:
Warunek ruchu elektronu:
=
(siła dośrodkowa jest równa sile elektrostatycznego przyciągania
elektronu przez jądro atomowe)
Warunek kwantowania:
=
(moment pędu L elektronu na danej orbicie jest proporcjonalny do
numeru orbity n, współczynnikiem proporcjonalności jest tzw. stała
Plancka „kreślona” (niekiedy – kreślna?)
————— = —————
=
Zależność promienia orbity elektronu od numeru orbity
(czyli od pierwszej, głównej liczby kwantowej)
rn
= ———————
Wniosek:
promień orbity elektronu jest . . . . . . . . . . . . . . .
do . . . . . . . . . . . . . . . . . . . . numeru orbity.
Punktów „. . . . . . . . . . .”, bo orbity są . . . . . . . . . . . . .
(nie ma stanów „pośrednich”).
[rn] =
r1
———––––––––––
= ———––––––––––––––––––———— = ——————— = ———————
Zatem średnica niewzbudzonego atomu to:
Promień drugiej orbity
r2 =
r3 =
d1 =
średnica wzbudzonego atomu to:
trzeciej:
Zależność natężenia E pola elektrycznego od numeru n orbity
(czyli od pierwszej, głównej liczby kwantowej)
E = ———— = —————— = ———————— =
—————
———————
d2 =
Zależność prędkości elektronu od numeru n orbity
(czyli od pierwszej, głównej liczby kwantowej)
= ———— = ——————————— = —————
—————
Prędkość elektronu na danej orbicie jest . . . . . . . . . . . .
[V1] = ————————
Obliczenia:
V1 = ——————————————————— = ————————————— =
Do prędkości światła . . . . . . . . .
V2 =
V3 =
Zależność okresu T ruchu elektronu po orbicie od numeru n orbity
(czyli od pierwszej, głównej liczby kwantowej)
————
Tn = ——— = ———————— = ———————
————
–––––––––––––
T1 = —––––––––––––––––––––—— = ––————————————————— =
Zależność pędu p elektronu od numeru n orbity (czyli od pierwszej, głównej liczby kwantowej)
Pn =
=
———— = ——————
Związek fal materii z budową atomu.
Długości fal, przypisanych elektronom na kilku kolejnych orbitach:
n = —— = —————— = ———————
—————
Ile długości fal de Broglie’a mieści się na kilku kolejnych orbitach?
——————
Xn = ——— = —————— = ——————————— =
——————
Czyli na pierwszej orbicie mieści się . . . . . . . . . fala de Broglie’a, na drugiej . . . . . . . . , na trzeciej
N=1
n=2
n=3
n=4
n=5
n=6
Energie w atomie wodoru
A. Kinetyczna:
————
EK = ———— = ——————— = ——————
B. Potencjalna:
EP = ———— = — ———— = — ——————— = = — —————
——————
C. Całkowita:
EC = EK + EP = —————— — —————— = — ———————
Podstawić wartości liczbowe dla pierwszej (n=1), drugiej (n=2) oraz trzeciej (n=3) orbity.
czyli obliczyć energię elektronu na kilku kolejnych orbitach, wynik podać również w elektronowoltach!!!
E1 = — —————————————————— = — ——————————————— =
E2 =
E3 =
E4 =
— seria Lymana – przeskok z dowolnej wyższej na . . . . . . . . . . . orbitę, . . . . . . . energie
fotonów, . . . . . . . częstotliwości, . . . . . . . . fale.
— ...............
— seria Balmera – przeskok z dowolnej wyższej na . . . . . . . . . . . orbitę, . . . . . . . . . . . . . .
energie fotonów, . . . . . . . . . . . . . częstotliwości, . . . . . . . . . . . . . . . fale.
— ........... ..............
— seria Paschena – przeskok z dowolnej wyższej na . . . . . . . . . . . orbitę
— seria Bracketta – przeskok z dowolnej wyższej na . . . . . . . . . . . orbitę
— seria Pfunda – przeskok z dowolnej wyższej na . . . . . . . . . . . orbitę
Elektron przy przeskoku z orbity dalszej na bliższą emituje energię w postaci fotonu, kwantu,
jego energia:
E =
=
EW = — ———————
EN = — ———————
E = EW — EN = — ———————— —
— ————————
=
= ———————— — ———————— = ———————
a więc:
=
= ———————
—— — ——
zaś
= —— = ———————
—— — ——
zatem:
—— = —————————
——— — ———
Stała Rydberga (do zadań z długością fali ):
R = ——————— = ———————————— = ———————————
———— = R ——— — ———
Jeśli w treści zadania jest „coś” powiedziane o serii, promieniowaniu, widmie ... granicznym, to
przeskok następuje „z” lub „na” orbitę . . . . . . . . . . . . . . .
np jeśli nW   to graniczna długość fali:
—— = R ———
Uwaga!
Wg niektórych podręczników stała Rydberga „opiera” się „na” częstotliwości:
R = ——— = ————————
—— — ——
wyznaczamy jednostki „stałych”(?) Rydberga,
oblicz wartości liczbowe „stałych”(?) Rydberga, porównaj z wartościami danymi w tablicach,
podręcznikach, encyklopediach, ...
Uwaga!
W „naszym” podręczniku stała Rydberga „opiera się” na ENERGII (strona 196):
Atom wieloelektronowy:
Opis formułuje się w dwóch krokach:
1. zaniedbuje się oddziaływania między . . . . . . . . . . . . . Stan kwantowy opisany jest za pomocą
liczb kwantowych atomu wodoropodobnego. Energia elektronu zależy tylko od . . . . . . . . . . . .
2. uwzględnia się oddziaływanie między . . . . . . . . . . . . .. Zastępuje się wpływ Z–1 elektronów
na dany elektron, średnim wytworzonym przez nie kulistosymetrycznym potencjałem, który
stanowi dodatek do kulombowskiego potencjału jądra atomowego.
Doświadczenie Francka – Hertza polegało na przepuszczeniu elektronów przez pary rtęci. Gdy
elektrony poruszały się powoli – atomy rtęci nie zakłócały ich ruchu. Po przekroczeniu pewnej wartości
energii następował gwałtowny spadek liczby elektronów. Jednocześnie atomy rtęci zaczęły świecić.
Matura „podstawowa” – grudzień 2005 – diagnostyczny – zadanie 20 (4 pkt)
W swobodnym, wzbudzonym atomie wodoru elektron przeskakuje z orbity drugiej na pierwszą. Atom
emituje wówczas w próżni kwant światła o długości fali 1,219  10 –7m.
a) Wyjaśnij dlaczego w wyniku emisji fotonu pęd atomu wodoru uległa zmianie. (2 pkt).
b) Oblicz energię emitowanego fotonu. (2 pkt)
Matura „podstawowa” – styczeń 2006 – zadanie 20 (4 pkt)
Wzbudzony atom wodoru emituje promieniowanie związane z przejściem elektronu z powłoki trzeciej
na drugą. Oblicz energię wyemitowanego kwantu i długość fali uzyskanej linii widmowej. Zapisz, czy
linia ta wypada w zakresie światła widzialnego, jeśli światło widzialne zawiera fale w przedziale od
380nm do 760nm, Energia stanu podstawowego atomu wodoru E = –13,6eV.
Matura „podstawowa” – maj 2007 – zadanie 20 (3 pkt)
Elektron w atomie wodoru przechodzi z orbity drugiej na pierwszą. Atom emituje wówczas światło,
którego długość fali w próżni wynosi 1,22  10 –7m.
1. Oblicz częstotliwość fali wysyłanej podczas tego przejścia (1 pkt)
2. Oblicz energię emitowanego fotonu. Wynik podaj w eV. (2 pkt)
Temat: Widma.
Matura „podstawowa” maj 2005 Zadanie 25.
Widmo to dowolne przedstawienie zależności „ . . . . . . . . . .” promieniowania elektromagnetycznego
od jego . . . . . . . . . . . fali lub . . . . . . . . . . . . . . . . . (częstości).
Przykład – tęczowe widmo światła widzialnego, uzyskane za pomocą . . . . . . . . . . lub . . . . . . . . . . .
Jasność każdego koloru w widmie pokazuje, jak silnie ów składnik przyczynia się do ogólnej jasności
źródła. Własności widma określa się metodami fotograficznymi lub przy użyciu detektorów
elektronicznych.
Sposoby rejestracji:
1. za pomocą . . . . . . . . . . . . . .
2. za pomocą . . . . . . . . . . . . . . . . . . . . . . . . . .
Widmo emisyjne to rozkład natężeń promieniowania elektromagnetycznego wysyłanego przez daną
substancję w funkcji . . . . . . . . . . . . . . lub . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Źródłem tego promieniowania są . . . . . . . . . . . . . . lub . . . . . . . . . . . . . . substancji (luminofor
scyntylatora) będące w stanie . . . . . . . . . . . . . .
W zależności od sposobu pobudzania rozróżniamy:
 widmo cieplne;
 termoluminescencje;
 elektronoluminescencje;
 elektroluminescencje;
 chemiluminescencję;
 fotoluminescencję.
Widmo liniowe – widmo promieniowania elektromagnetycznego o dyskretnym rozkładzie natężenia
w funkcji . . . . . . . . . . . . . . . fali lub . . . . . . . . . . . . . . . .. Składa się z wielu linii spektralnych,
spośród których dają się wydzielić . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Liczba linii oraz ich
położenie w widmie charakteryzuje . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., którym zwykle są . . . . . . .
. . . . . . . . lub . . . . . . . . . . . . . . . . (para lub gaz jednoatomowy). Natężenie linii widmowej zależy od
ilości . . . . . . . . . . . . . . . w substancji promieniującej.
Widmo ciągłe:
Widmo liniowe emisyjne:
Widmo liniowe absorpcyjne:
Rozkład natężenia promieniowania elektromagnetycznego w funkcji . . . . . . . . . . . . . . lub . . . . . . . . .
fali po przejściu przez substancję, która . . . . . . . . . . . . . . fale elektromagnetyczne o charakterystycznych dla siebie częstotliwościach. Lokalizacja linii widmowych w widmie atomów i prostych cząsteczek
jest identyczna z pozycją odpowiadających linii . . . . . . . . . . . . . . (zasada Kirchhoffa).
Widmo ciągłe:
IR
UV
Liniowe widmo wodoru:
Absorpcyjne widmo wodoru:
Widmo pasmowe czyli widmo . . . . . . . . . . . . . . . . . (molekularne). To widmo . . . . . . . . . . lub . . . . . .
. . . ., powstające przy przejściach między poziomami energetycznymi swobodnych lub słabo między
sobą oddziałujących . . . . . . . . . . . . Obserwuje się pasma . . . . . . . . . ., które dają się rozdzielić na
zbiory, blisko siebie położonych . . . . . . . . . . . . . . . . . . . .
Pasma spowodowane są ruchem:
 . . . . . . . . . . . . . . . . . . . .;
 . . . . . . . . . . . . . . . . . . . . jąder atomowych;
 . . . . . . . . . . . . . . . . . . . . cząsteczek jako całości.
Przejściu między poziomami energetycznymi cząsteczki towarzyszy . . . . . . . . . . lub . . . . . . . . .
fotonu o częstotliwości:
Zauważono relację:
Widmo ciągłe:
Liniowe pasmowe N :
Analiza widmowa.
Spektroskopowa metoda badania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . substancji. Wykorzystuje
niezmienność częstotliwości linii emisyjnych gazów rozrzedzonych. Pary nieznanej substancji
pobudza się do świecenia, a potem porównuje się otrzymane widmo ze znanymi widmami emisyjnymi.
Można określić, jakie pierwiastki wchodzą w skład nieznanej substancji.
Przykład: badanie zewnętrznych (gazowych) warstw Słońca – atmosfery słonecznej. Tak stwierdzono,
że w atmosferze słonecznej jest większość pierwiastków występujących na Ziemi (wodór, sód, hel,
potas . . . ) Hel odkryto najpierw na Słońcu.
Linie Fraunhoffera – . . . . . . . . . . . . . . . . . . linie na tle . . . . . . . . . . . . . . . . . . widma Słońca.
Widmo ciągłe:
Widmo słoneczne (z liniami Fraunhoffera)
Warto zauważyć, że między widmami rentgenowskimi a optycznymi występuje istotna różnica. Widmo
optyczne zależy od stanu skupienia substancji. Gazy dają ostre widma . . . . . . . . . . . . . . . . . . Ciecze
i ciała stałe dają widma . . . . . . . . . . . . . . . lub . . . . . . . . . . . . . . Widma rentgenowskie nie zależą
ani od . . . . . . . . . . . . . . . . . . . . . . . . . . . ., ani nawet od tego, czy atomy występują w stanie
wolnym, czy też wchodzą w skład związków chemicznych. Ta własność wynika stąd, że powstają
w wyniku przejść elektronowych między . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., które są
nieporównywalnie . . . . . . . . . . wrażliwe na wpływ otoczenia.
Temat: Lasery.
Light Amplification by Stimulated Emission of Radiation – wzmocnienie światła przez wymuszoną
emisję promieniowania.
MASER: Microwave Amplification by Stimulated Emission of Radiation – wzmacniacz mikrofalowy
kwantowy, wykorzystujący emisję wymuszoną.
Następna stacja: Jądro atomowe.