NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
NANOSTRUKTURY
X – XII 2012
Wysłuchał, spisał i opracował
Piotr Klejment
UWAGA!!!
NINIEJSZE OPRACOWANIE
MOŻE ZAWIERAĆ BŁĘDY!
1
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
KOLOKWIUM 1
Zadania na kolokwium
Wybrać dwa pytania i opisać
1) Gęstość stanów elektronowych. Porównać i przedyskutować dla stanów o różnej
wymiarowości.
2) Omów zjawisko TMR i jego zastosowania
3) Skaningowy mikroskop tunelowy. Przedyskutować różne mody pracy mikroskopu.
2
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
NANOSTRUKTURY
wykład I
Struktury niskowymiarowe: struktury, w których co najmniej jeden kierunek jest rzedu
h
długości fali de Broglie’a dla elektronu λ =
p
Wyróżniamy struktury:
3D: materiały masywne – nie ma kwantowania w żadnym kierunku
2D: studnie kwantowe – kwantowanie w jednym kierunku
1D: druty kwantowe - kwantowanie w dwóch kierunkach
0D: kropki kwantowe – kwantowanie we wszystkich kierunkach
Grafen: dwuwymiarowy kryształ złożony z atomów węgla tworzących sieć heksagonalną.
Każdy kryształ charakteryzuje się dalekozasięgowym uporządkowaniem (takie
uporządkowanie występuje tylko w 3D). Istnieje możliwość uporządkowania w 2D w
nanokrytstalitach. Grafen wykazuje szczególne właściwowści elektronowe – elektrony jako
bezmasowe cząstki. Pasmo przewodnictwa i walencyjne grafenu łączą się dokładnie w 6
punktach. W grafenie występuje liniowa relacja dyspersji, jak w fononach i innych bozonach.
Pełna symetria między elektronami i dziurami.
Tranzystor zbudowany na grafenie: nie wymaga szczególnych warunków (clean room).
Zmieniając napięcie bramkowe zmieniamy położenie poziomu Fermiego. Mała rezystancja
dla poziomu Fermiego w paśmie, po przejściu poziomu Fermiego przez punkt doracowski
mocno rośnie.
Drut kwantowy: w jednym kierunku elektron może poruszać się jako swobodny, w
pozostałych mamy kwantowanie (można traktować jako studnie). Quasi – ciągłe wartości
energii w kierunku swobodnego ruchu i podpasma nazywane modami w kierunku dyskretnym
energii. W kierunku swobodnym fala płaska, w pozostałych stojąca. Otrzymuje się druty
kwantowe ze studni kwantowych, poprzez litografię i trawienie brzegów studni, a następnie
nakładamy na strukturę dwie elektrody i przykładamy silny ujemny potencjał. Elektrony
zgromadzą się w kanale miedzy elektrodami dając drut kwantowy.
Kropka kwantowa: odległości między poziomami energetycznymi >kT, żeby energia
wzbudzeń termicznych nie niszczyła kwantowania. Układy kropek są ważne ze względu na
właściwości optyczne.
Antykropki kwantowe: wycięte w matryce grafenowej małe obszary.
Inne nanoobiekty mogą odgrywać rolę kropek jak nanokrytality otrzymywane w
zawiesinach koloidalnych, czy molekuły.
Nanorurka węglowa: płaszczyzna grafenowa zwinięta w tubę z symetrią periodyczną na
obwodzie rurki. Mają własności elastyczne i największy moduł Younga ze znanych
materiałów. Występuje w nich transport balistyczny.
3
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Blokada kulombowska: efekt w tranzystorze, gdy na tranzystorze znajduje się wyspa i jeżeli
jej pojemność będzie odpowiednio mała, to zaobserwujemy blokadę kulombowską, czyli
oddanie lub zabranie jednego elektronu z wyspy. Zmieniając napięcie bramkowe można
blokować blokadę kulombowską i otrzymać oscylacje przewodności. Jeżeli między źródłem,
a drenem przyłożymy napięcie, to na charakterystyce pojawią się charakterystyczne stopnie
zwane stopniami kulomba.
Interferencja kwantowa: transport opisywany jest inaczej niż w układach masywnych, bo
elektron jest falą, co ma duży wpływ na właściwości transportu. Fala elektronowa od źródła
elektronów dociera do „pierścienia”, gdzie zostaje rozdzielona na dwie fale. Fale poruszają
się górnym i dolnym kanałem. Na wyjściu fale nakładają się na siebie, czyli zachodzi
interferencja.
Nanoelektronika: oparta na nanorurkach.
Gigantyczny magnetoopór: typowy efekt warstwowych struktur metalicznych, można
opisywać go klasycznie.
Kwantowy magnetopór: dwie warstwy metaliczne przedzielone niemagnetyczną przekładką.
Jeżeli momenty magnetyczne są równoległe, to cały ten układ wykazuje mały opór. Przy
zmianie kierunku namagnesowania warstwy wzrost rezystancji. W przypadku złącz
tunelowych w niskich temperaturach zmiana rezystancji może być do 1000%.
Własności elektronowe zdefiniowane są przez strukturę. Dla układów krystalicznych ważną
rolę odgrywa symetria sieci. Przesuwając o dowolny wektor sieci prostej otrzymujemy to
samo ze względu na periodyczność sieci.
Gęstość stanów: liczba stanów energetycznych na jednostkę energii.
WYTWARZANIE STRUKTUR NISKOWYMIAROWYCH
wykład II
Epitaksja: obsadzanie warstwy na podłożu krystalicznym. Metody epitaksjalne pozwalają na
najdokładniejszą kontrolę rosnących warstw.
Wytwarzanie struktur niskowymiarowych:
Najprecyzyjniejszą metodą jest epitaksja z wiązek molekularnych MBE, która
stosuje się do układów metalicznych i półprzewodnikowych. Taką epitaksję prowadzi
się w komorach o wysokiej próżni, co jest jednocześnie wadą, gdyż potrzebne są clean
roomy. Warstwy rosną wolno.
Epitaksja ze związków metaloorganicznych MOCVD to metoda bardziej
przemysłowa. Materiałem wejściowym jest gaz, który dysocjuje, a na podłożu osadza
się arsenek galu. Słaba jakość warstw, ale warstwy rosną stosunkowo szybko.
Epitaksja z wiązki chemicznej: połączenie dwóch poprzednich metod. Próbka rośnie
na podłożu w wysokiej próżni. Materiałami wejściowymi są gazy, które po
wprowadzeniu do komory ulegają dysocjacji. Pośrednia kontrola nad wzrostem.
Epitaksja z fazy gazowej: transport cząsteczek przez fazę gazową, wbudowywanie
się cząsteczek par do kryształu.
4
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Epitaksja z fazy ciekłej: płynny stop wylewa się na płytkę podłoża. Szybki wzrost,
wysoka jakośc warstw.
Homoepitaksja: podłoże ma taką samą strukturę krystaliczną jak hodowana warstwa.
Heterostruktury półprzewodnikowe: struktury składające się z kilku warstw
półprzewodnikowych. Tworzy się je w celu uzyskania pożądanych właściwości urządzenia.
Heterostruktury – sposoby wzrostu warstw:
warstwa po warstwie Franka – van der Merve’a
wyspowy Vollmera – Webera
mieszany Strańskiego – Krastanowa: najpierw wzrost warstwowy, a po przekroczeniu
pewnej grubości, następuje przejście fazowe i wzrost wyspowy. Grubość warstwy,
którą możemy nałożyć na podłoże, by układ był stabilny, nazywamy krytyczną.
Jakość hodowanej struktury zależy od dopasowania sieciowego podłoża i warstwy, a także
od energii powierzchniowej materiału, podłoża i interfejsu warstwa-podłoże.
Supersieci: układy z półprzewodników wąsko i szeroko przerwowych. Są to periodyczne
układy studni i barier, w których występuje przekrywanie się funkcji falowych, a w efekcie
tunelowanie elektronów i powstawanie minipasm. Jest to struktura quasi 3D.
Niebieski laser: GaN ma na tyle szeroką przerwę energetyczną, że istnieje możliwość
wyhodowania niebieskiego lasera. Może się to stać w procesie homoepitaksji, gdy warstwa
GaN-u będzie rosła na objętościowym GaN-ie. Problemem jest wytworzenie objętościowego
GaN-u, gdyż wymaga wysokiej temperatury i wysokiego ciśnienia.
Niebieska dioda: po odpowiednim dopasowaniu przerw energetycznych i stałych sieci GaN
na szafirze daje niebieską diodę.
Wytwarzanie drutów i kropek kwantowych LDS: potrzebne są metody pozwalające na
ściśnięcie elektronów w odpowiedniej ilości kierunków. Punktem wyjściowym jest studnia
kwantowa.
popularną metodą jest litografia: wyhodowaną warstwę pokrywa się polimerem, a
potem naświetla przez odpowiedni czas. W wyniku naświetlenia polimer można łatwo
usunąć, a puste miejsce pokrywa się maską ze złota. Po usunięciu pozostałego
polimeru wykonuje się trawienie chemiczne.
selektywny wzrost
ścinanie powierzchni
elektrostatycznie: na strukturę nakładamy elektrody do których przykładamy ujemny
potencjał.
na powierzchnię hodowanej struktury nakładamy lokalne modulacje, a elektrony będą
się gromadzić w miejscach najsłabszego potencjału tworząc matrycę kropek.
kropki samorosnące: wykorzystuje się przejście fazowe Strańskiego – Krastanowa.
kropki rosnące w zawiesinach koloidalnych, nanokryształki: powstają w wyniku
wygrzewania szkła kwarcowego, odgrywają rolę kropek.
w wyniku podgrzewania laserem ścianek studni w miejscach nagrzanych powstają
kropki
5
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
BADANIE STRUKTUR
wykład III
Skaningowy Mikroskop Tunelowy STM: pozwala na pomiar prądu tunelowego pomiędzy
badaną powierzchnią i igłą mikroskopu. Dzięki STM można uzyskać informacji o gęstości
stanów, badać topografii powierzchni próbki lub przesuwać atomy na powierzchni
przewodzącej. Do sterowania igłą stosuje się elementy piezoelektryczne. Jedną z elektrod jest
igła, a drugą skanowana powierzchnia. Jako igły stosuje się nanorurki. Badanie zachodzi w
niskiej temperaturze, aby zniwelować ruchy Browna. W celu uzyskania najwyższej,
jednoatomowej rozdzielczości, większość prądu powinna płynąć przez jeden atom – ostrze
skanujące powinno być zakończone jednym atomem.
Mody pracy STM:
stała wysokość ostrza – ostrze na stałej wysokości nad badaną powierzchnią, a
informacja o badanej powierzchni jest dana przez rozkład natężenia prądu tunelowego
stały prąd tunelowania – regulowana wysokość ostrza, aby utrzymać stały prąd w
układzie
spektroskopowy – charakterystyka prądu tunelowego I(V) przy stałej wysokości ostrza
STM pozwala na określanie gęstości stanów, czemu zawdzięczamy efekt Kondo i miraż
kwantowy. Efekt Kondo występuje na wskutek obecności domieszki magnetycznej, która
prowadzi do podwyższenia gęstości stanów na poziomie Fermiego na, wskutek czego pojawia
się wysoki pik w gęstości stanów prowadzący do silnego rozpraszania elektronów w
materiałach masywnych. W materiałach kwantowych pik Kondo w pobliżu poziomu
Fermiego ułatwia tunelowanie i prowadzi do wzrostu przewodności. Ponieważ elektrony
ułożone są w elipsę, obserwuje się pik Kondo również w miejscu drugiego ogniska, chociaż
nie ma tam atomu - wynika to z geometrii elipsy, a efekt taki nazywa się mirażem
kwantowym.
Dzięki STM można manipulować atomami – atomowy mogą być przesuwane przy
wykorzystaniu sił van der Waalsa. Z kolei przy zastosowaniu silnego (impulsowego) pola
elektrycznego możliwy jest przeskok atomu z powierzchni do igły i odwrotnie.
Spektroskopia tunelowa: w układzie z dwiema barierami tunelowymi szerokość barier łatwo
zmierzyć poprzez zmianę odległości igły i kropki kwantowej. Elektron tuneluje z igły na
kropkę i do podłoża. Można dzięki temu uzyskać informacje o dyskretnych poziomach
kwantowych. takie same wyniki pozwalają uzyskać pomiary optyczne.
Mikroskop sił atomowych AFM: najbardziej podstawowe narzędzie do badania
nanostruktur, w którym wykorzystano koncepcję sił harmonicznych. Pozwala na uzyskanie
informacji o topologii powierzchni. Igła skanuje powierzchnię, przy czym mierzona jest siła
oddziaływania pomiędzy powierzchnią, a igłą. Zmiany sił dają informację o topografii
powierzchni. Dzięki AFM możemy zbadać dwa ważne zjawiska w półprzewodnikach:
potencjał powierzchniowy oraz rekonstrukcje powierzchniowe (przegrupowanie atomów w
celu uzyskania najniższej energii).
6
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Tryby pracy AFM:
tryb kontaktowy: o dużej rozdzielczości obrazów, duże siły adhezyjne spowodowane
obecnością zanieczyszczeń powierzchni, możliwość uszkodzenia próbki lub ostrza
tryb bezkontaktowy: mniejsza rozdzielczość obrazów
tryb z przerwanym kontaktem: pozwala na badanie miękkich powierzchni, dobra
zdolność rozdzielcza, rejestruje zmiany amplitudy drgającej igły
Mikroskop sił magnetycznych MFM: wykorzystuje siły magnetyczne, wymaga struktury
domenowej. Igła pokryta jest warstwą magnetyczną i reaguje na zmiany pola w czasie
przemieszczania nad powierzchnią. Wadą takich pomiarów jest słaba zależność od odległości.
ZJAWISKA TRANSPORTU
TRANSPORT SPINOWO ZORIENTOWANYCH ELEKTRONÓW
wykład IV
ZJAWISKA TRANSPORTU
Energia Fermiego: wartość energii, która oddziela stany obsadzone i nieobsadzone w T =
0K.
Transport: ukierunkowany ruch elektronów pod wpływem czynników zewnętrznych np. pola
elektrycznego E. Transport nośników ładunku w ciałach stałych zależy do procesów ich
rozpraszania. Elektrony, zderzając się z innymi elektronami albo rozpraszając na drganiach
sieci krystalicznej, defektach albo granicach zmieniają swój stan. Średnia droga, którą
przechodzi elektron między dwoma kolejnymi aktami rozpraszania nosi nazwę średniej drogi
swobodnej. Transport wygląda inaczej w obiektach niskowymiarowych niż masywnych.
Quasi-klasyczna teoria transportu: transport w materiałach masywnych ma charakter
dyfuzyjny w oparciu o klasyczne równanie Boltzmanna, w niskowymiarowych w oparciu o
równanie Fermiego-Diraca. Główny wkład do transportu dają elektrony w pobliżu poziomu
Fermiego. W układy niskowymiarowych występuje transport balistyczny: elektron emitowany
jest przez układ, co najwyżej odbija się od granic próbki. W materiałach masywnych transport
dyfuzyjny: elektron często się odbija.
Efekty kwantowe ważne są dla układów o rozmiarach rzędu długości fali.
Czas relaksacji fazy: czas, po którym elektron zapomina swoją fazę. Faza elektronu eikr
gdzie kr to czynnik fazowy.
Długość koherencji fazy: istotny czynnik charakteryzujący transport kwantowy. Jest to
odległość, na której elektron zachowuje pamięć fazową.
Gdy badamy transport w nanostrukturach, wprowadza się współczynnik proporcjonalności G
– zależność między prądem i napięciem, odwrotność rezystancji, nazywany przewodnością (δ
→
→
to przewodnictwo). Przewodność to I = GV , a przewodnictwo j = σ E
7
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Charakterystyka I-V: po przyłożeniu napięcia zmienia się kształt bariery. Transmisja zależy
od napięcia i napięcie wchodzi w funkcję Fermiego – Diraca. Dla małych napięć można je w
transmisji zaniedbać. Taki efekt najczęściej w diodzie tunelowej jest wykorzystywany.
Pojawia się pojedyncza wąska bariera po przyłożeniu napięcia.
TRANSPORT SPINOWO ZORIENTOWANYCH ELEKTRONÓW
Półprzewodniki nie wykazują właściwości magnetycznych.
Pole koercji: pole potrzebne do zmiany kierunku pola magnetycznego.
Zawór spinowy: zawiera dwie warstwy, w tym jedną o ustalonym momencie magnetycznym.
Używa się w nich syntetycznego ferromagnetyka – nałożonej w wysokich temperaturach
warstwy ferromagnetycznej schłodzonej następnie w polu.
Tunelowy magnetoopór TMR: zwany też zjawiskiem Gaussa, polega na
zmianie oporu metali i półprzewodników pod wpływem pola magnetycznego. Praktyczne
zastosowanie w magnetoopornikach. W polu magnetycznym tor cząstki naładowanej
zakrzywia się, więc droga jaką pokonuje cząstka ulega wydłużeniu. Objawia się to
zmniejszeniem natężenia prądu (wzrostem oporu). Zjawisko Gaussa wykorzystywane jest do
pomiaru natężenia pola magnetycznego.
TMR jest proporcjonalny do iloczynu polaryzacji obu ferromagnetyków, gdzie polaryzacja
jest określona przez gęstość stanów na poziomie Fermiego. Z modelu Julliera wynika, że tym
większe TMR im większa polaryzacja. TMR maleje dość silnie z temperaturą, a także
napięciem. Efekt TMR wykorzystuje się w pamięciach dysków twardych.
TMR dla złącz krystalicznych: tunelowy magnetopór zależy od iloczynu polaryzacji
obydwu złącz. Im większa polaryzacja, tym większy magnetopór.
Złącza tunelowe mają większe zalety niż złącza metaliczne:
w złączach tunelowych prąd zawsze płynie prostopadle do granic,
mniejsze rozmiary
bardziej odporne na temperaturę,
stabilniejsze
możliwa jest w nich większa gęstość zapisu.
duży efekt TMR.
większy opór niż metaliczne.
Zapis informacji (1,0) to ustalenie momentu magnetycznego. Mamy dwie linie, wzdłuż
których możemy przepuszczać prąd. Prądy płynące przez obie linie się sumują, co daje dość
duże pole magnetyczne, żeby obrócić moment magnetyczny jednej komórki.
Spintronika półprzewodnikowa: elektronika spinowa, w której wykorzystuje się efekty
spinowe. Złącze tunelowe: warstwy swobodna i referencyjna to warstwy metaliczne ze
8
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
względu na właściwości ferromagnetyczne, a przekładka to izolator. Problemem jest
zapewnienie współpracy metalu z półprzewodnikami. Rozwiązania problemu to:
wstrzykiwanie spinów do półprzewodnika lub wynalezienie magnetycznego półprzewodnika
mającego wysoką temperaturę Curie (temperatura, powyżej której znikają właściwości
magnetyczne).
Spintronika molekularna: metaliczne elektrody i nanorurka, wysokie TMR, ale w niskich
temperaturach.
Inna linia poszukiwań to zwiększenie TMR przez zwiększenie polaryzacji.
Ferromagnetyki półmetaliczne: nie istnieją samoistnie. Są odpowiedzią na próby uzyskania
materiałów o wysokiej polaryzacji. Mają wyrafinowaną strukturę pasmową i szczególną
strukturę krystaliczną np. spinele, stop Heuslera z przerwą energetyczną dającą zerową
gęstość stanów dla zerowego jednego kierunku spinu.
Spinowy moment obrotowy STT: istotny krok w spintronice, pozwala na manipulowanie
momentem magnetycznym bez obecności pola magnetycznego. Mając prąd spinowy i spin
kolinearny z momentem warstwy, do której płynie prąd, to następuje transfer spinów. Zostaje
wymuszony kierunek pionowy momentu magnetycznego, a składowa pozioma jest
absorbowana. Transfer momentu magnetycznego wiąże się z momentem obrotowym i
wchodzące elektrony będą działały momentem obrotowym na kierunek warstwy, do której
wnikają i w pewnych warunkach mogą obrócić moment magnetyczny. Jest to efekt transferu
spinów, a nie pola magnetycznego.
Po umieszczeniu momentu magnetycznego w polu magnetycznym o innym kierunku pojawia
się precesja. W realnych układach pojawia się też tłumienie precesji, aż moment
magnetyczny ustawi się w kierunku równoległych do pola magnetycznego. Jeżeli STT jest na
tyle duży, że znacznie przeważa nad tłumieniem, to możemy obserwować przełączanie –
zmianę momentu i rezystancji. Efekt ten wynika z transferu spinów.
Zjawiska termoelektryczne w nanostrukturach: efekt Seebecka, czyli gradient temperatury
generuje napięcie na krańcach przewodnika, efekt Peltiera, czyli różnica temperatur
pojawiająca się w wyniku przepływu prądu.
Przewodność cieplna grafenu: najwyższe przewodnictwo cieplne, znaczną siłę
termoelektryczną można uzyskać, duże przewodnictwo elektryczne, brak wkładu od
elektronów.
Spinowa kalorymetria: efekty termoelektryczne w układach
Magneto termo siła: siła termoelektryczna generowana przy równoległej konfiguracji obu
elementów złącza minus siłą przy konfiguracji antyrównoległej.
Gigantyczna magnetorezystancja GMR polega na znacznej zmianie rezystancji
wielowarstwowego układu, składającego się z ferromagnetycznych metalicznych
warstw, oddzielonych od siebie przewodzącymi, nieferromagnetycznymi warstwami
Zewnętrzne pole magnetyczne wywołuje zmianę względnej orientacji momentów
magnetycznych ferromagnetycznych warstw, co wywołuje znaczną zmianę
magnetooporu.
9
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
KOLOKWIUM 2
10
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
REZYSTANCJA W UKŁADACH KLASYCZNYCH I KWANTOWYCH
wykład VI
VI
Formuła Landauera: dwa kontakty połączone są za pomocą przewodnika balistycznego, a
T(E) określa transmisję. Ppór przewodnika i jego przewodność są skwantowane.
W idealnym przewodniku balistycznym T=1, czyli przewodność G =
2e 2
M . Rezystancja
h
h 1
. W idealnym przewodniku balistycznym opór
2e 2 M
pojawia się na granicach z kontaktami, jest to opór kontaktowy. Opór kontaktowy jest
odwrotnie proporcjonalny do liczby modów M. Dla przewodników rozciągłych liczba modów
wzrasta, powodując, iż opór kontaktowy staje się zaniedbywanie mały.
idealnego przewodnika R = Gc−1 =
Rezystancja kontaktowa: gdy liczba modów jest duża (połączone dwa kontakty), to opór
kontaktowy będzie dążył do zera. Przykład: gdyby przewodnik metaliczny miał przekrój
2000x2000 [atomów] to mamy 106 modów. Rezystancja 10kΩ/106 będzie oczywiście zerowa.
Wynika z tego, że rezystancja kontaktowa jest istotna dla niewielkiej liczby modów.
Formuła Landauera uogólniona dla transportu dwukanałowego: dwa kontakty i
przewodnik, w którym następuje rozpraszanie. Transmisja jest skończona, gdyż mod
wchodzący inny niż wychodzący. Całkowita transmisja to suma po wszystkich modach
wchodzących. W przypadku, gdy mody ze sobą nie oddziałują, to mówimy o kanałach.
Formuła Landauera G =
2e 2
MT
h
Rezystancja - podejście klasyczne: rozpatrujemy dwa centra rozpraszające znajdujące się w
odległości większej niż długość koherencji fazy (nie ma korelacji faz). Elektron rozpraszany
znajduje się na pierwszym centrum - zanim zdąży dotrzeć do drugiego centrum, zapomina
T
swoją fazę. Iloczyn 1 określa bezpośrednią rezystancję, ale trzeba uwzględnić jeszcze
T2
odbicia. Całkowita transmisja to T1T2 R1 R2 plus akty wielokrotnego rozpraszania niezwiązane
fazowo na wskutek dużej odległości między centrami.
Po rozwinięciu w nieskończony szereg geometryczny i obliczeniu jego sumy, otrzymamy
T1T2
.
całkowitą transmisję dla dwóch centrów
1 − R1 R2
Transmisja przewodnika o długości L
1− T
Wielkość
wykazuje cechy addytywności. Jeżeli będziemy mieli drut z N identycznymi
T
centrami rozpraszającymi na długości L, wówczas całkowita transmisja wyniesie
11
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
T (N ) =
T
. Gdyby uzależnić te wyrażenie od długości drutu to otrzymamy
N (1 − T ) + T
L0
T (L ) =
– wielkość odwrotnie proporcjonalną do długości drutu.
L + L0
Prawo Ohma
Wprowadzamy:
υ – ilość centrów na jednostkę długości, gdzie υ =
N
L
T
υ (1 − T )
1-T - prawdopodobieństwo rozproszenia przez centrum
L0 - współczynnik rzędu drogi swobodnej L0 =
h 1 1−T
h
h 1−T
= 2 + 2
= Gc−1 + Gs−1
2
2e M T
2e M 2e M T
Gc-1 to opór kontaktów, a Gs-1 to opór wynikający z rozpraszania.
Opór przewodnika M-modowego G −1 =
Prawdopodobieństwo rozproszenia na drodze Lm wynosi (1 − T )υLm , co w przybliżeniu równa
się 1.
Wniosek: rezystancja półprzewodnika N - modowego, będzie równa oporowi kontaktów i
oporowi wynikającemu z rozpraszania. Rezystancja ta rośnie liniowo z długością, co jest
zgodne z prawem Ohma.
Przejście do szerokiego przewodnika.
Wprowadzamy:
liczba modów w przewodniku M =
W
λF
2
2Π
λF =
– z wyrażenia tego należy wziąć wielkość całkowitą.
kF
k F = mυ F T
m
g 2 D = 2 - gęstość stanów w 2D przewodniku
h n
W – szerokość przewodnika,
L0
T=
transmisja
L + L0
σW
G=
przewodność
L + L0
L
L
L
Wówczas R = G −1 = 0 +
= GC−1 +
z czego ostatni człon to rezystancja właściwa.
σW σW
σW
12
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
W tych rozważaniach przekrój poprzeczny to tylko szerokość, gdyż trzeci wymiar jest
infinitezymalnie mały. Wszystkie powyższe rozważania dotyczą przypadków klasycznych.
Transmisja: w niskich temperaturach szczególnie półprzewodniki mają dużą długość
koherencji fazy. Jeżeli mamy pełną koherencję fazy przy przejściu przez dwa centra
ropraszające,
wówczas dzielimy półprzewodnik na jednostki mające koherencję fazy (miedzy jednostkami
koherencji już nie ma). W takiej sytuacji należy już uwzględnić efekty kwantowe.
Przewodność obliczona kwantowo jest mniejsza. Wynika to z faktu, iż na ogół rozpraszane
układy mają pewną liczbę centrów rozpraszających. Można przyjąć, że każdy mod
rozpraszany jest z jednakowym prawdopodobieństwem. Tak sytuacja wygląda klasycznie.
W przypadku kwantowym, gdy mod wchodzący i wychodzacy są takie same i = j , to
przypadek jest klasyczny, gdy i ≠ j należy uwzględnić koherentne rozpraszanie wsteczne:
amplituda fali rozproszonej posiada maksimum na kierunku fali padającej.
Przykładamy ścieżki A(m → n ) . Kwadrat sumy amplitud fal odbitych dla wszystkich
możliwych dróg da prawdopodobieństwo odbicia R ze stanu m do n. Ścieżki A są losowe,
więc czynniki fazowe będą się ostatecznie znosić i przypadek będzie klasyczniy.
Istnieje jedna jedyna ścieżka, dla której będzie inaczej, ponieważ zawsze istnieje dla niej
ścieżka odwrotna ze względu na inwersję czasu.
2
R (m → n ) = ( A1 + A1r + ...) = 4 A , a nie 2|A|2
Jest to efekt koherentnego rozpraszania wstecznego.
Dla każdej ścieżki innej niż ta wyjątkowa, wspomniana powyżej, R=2|A|2. Ścieżka, która
zaczyna i kończy się tym samym modem jest wyróżniona, gdyż dodajemy dla niej amplitudy,
a nie prawdopodobieństwa.
2e 2
h
Ostatni człon w tym wyrażeniu oznacza obniżenie przewodności o tę jedną szczególną
scieżkę, wkład ten jest nieistotny dla niewielkiej liczby modów.
Średnia przewodność liczona kwantowo Gkw = K kl −
13
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
UKŁADY W POLU MAGNETYCZNYM. EFEKT HALLA.
wykład VII
VII
Interferencje kwantowe: mamy falę elektronową, która dochodzi do punktu, w którym
następuje rozdzielnie na dwie fale. Na wyjściu następuje nałożenie, wynik będzie zależał od
faz. Otrzymamy współczynnik transmisji periodycznie zależny od k1 i k2.
Układ z równoległym połączeniem dwóch rezystancji. Jeżeli będziemy sumować wszystkie
mody to przewodność będzie oscylowała w zależności od różnicy faz. Interferencję można
zauważyć w efekcie Aharonova – Bohma. Możemy sterować przewodnością zmieniając
h
pole. Iloczyn pola razy powierzchnia obejmowana przez pierścień to
- kwant strumienia
e
h
, to mamy oscylacje
e
przewodności. Rozmiary pierścienia musza być odpowiednio małe, aby istotne były efekty
interferencji kwantowej. Interferencję kwantową niszczy temperatura.
elektromagnetycznego. Jeżeli strumień będzie wielokrotnością
Efekt Aharnova – Bohma: daje możliwość sterowania efektami interferencyjnymi fal
elektronowych za pomocą pola magnetycznego. Przewodność pierścienia oscyluje w funkcji
strumienia magnetycznego obejmowanego przez ten pierścień,
Mamy falę elektronową i musimy rozważyć transmisję T1 i T2 wzdłuż górnego i dolnego
półpierścienia. Transmisja w polu to transmisja bez pola razy zmiana fazy, φ – zmiana fazy.
Faza w funkcji falowej może się zmieniać w wyniku zmian energii itd.
W przypadku pierścienia liczymy fazę wzdłuż górnego i dolnego półpierścienia. Całkowita
zmiana fazy pochodzi tylko z obecności pola magnetycznego eikr − ∆ϕ −ωt . Pierścień musi być
cienki, żeby strumień przechodził całkowicie wewnątrz pierścienia.
→
Przy dużym pierścieniu czynnik fazowy będzie sie uśredniał do zera. Mod wchodzący m ,
→
wychodzący n , musimy zsumować po wszystkich modach. Mody diagonalne będą się
sumowały, bo dla niediagonalnych fazy będą się upraszczać.
Temperatura niszczy efekty interferencyjne. Efekt Aharonova-Bohma to najbardziej
podstawowy efekt, w którym można obserwować interferencję.
14
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Interferencja kwantowa w grafenie: elektrony wędrują po różnych ścieżkach, sumujemy po
wszystkich ścieżkach. Zmiana fazy zależy od pola magnetycznego, konfiguracji domieszek i
położenia poziomu Fermiego. W przypadku grafenu można otrzymać różne wyniki w
zależności od położenia poziomu Fermiego.
Przewodność mierzymy w funkcji napięcia bramkowego, a napięcie bramkowe pozwala na
sterowanie poziomem Fermiego. Oscylacje są efektem interferencji kwantowych.
UKŁADY NISKOWYMIAROWE W POLU MAGNETYCZNYM
Równanie ruchu w polach E i B można przepisać w postaci macierzowej, a następnie
wprowadzamy gęstość prądu zamiast prędkości unoszenia.
Rezystancja podłużna nie ulega zmianie, rezystancja poprzeczna rośnie z polem, czyli
V
otrzymujemy klasyczny efekt Halla ρ yx = H
I
Poziomy Landaua: wprowadzamy silne pole magnetyczne. Gdy pole jest odpowiednio silne,
tworzą się poziomy Landaua i elektrony będą się na nich gromadziły. Ma to miejsce w
każdym wymiarze.
→
→
→
B = rot A pole wybieramy równolegle do osi z B || z
Rozważamy 2D gaz elektronowy (np. wąska studnia kwantowa z arsenku galu), na granicy
występuje gaz elektronowy, opisujemy hamiltonianem. Po wycechowaniu otrzymujemy
modyfikację składowej x pędu. Funkcja opisująca ruch elektronu Ψ ( x, y ) .
Otrzymujemy nową postać hamiltonianu, wprowadzamy oznaczenie ωc – częstość
cyklotronową. Otrzymujemy równanie oscylatora harmonicznego centrowanego w punkcje
y=k. Otrzymujemy równanie, z którego wynika, że mamy szereg równoodległych poziomów
zwanych poziomami Landaua.
Elektrony w 2D gazie poruszają się w po 2D okręgach i gromadzą na poziomach Landaua.
15
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Odległość między poziomami będzie rosła z polem. Poszczególne oscylatory centrowane są w
punkach k.
Stopień degeneracji określa wzór N =
φ
. Strumień obejmowany przez powierzchnię jest
φ0
wielokrotnością strumienia. Jeżeli pole rośnie, to rośnie liczba elektronów, które mogą się
znaleźć na poziomach Landaua.
Filling Factor – określa zapełnienie poziomów Landaua.
Poziomy Landaua w 1D: zmniejszamy W w stosunku do L i wprowadzamy potencjał
wiążący. Pozostajemy w tej samej geometrii, ale pole jest prostopadłe do paska tym razem, a
nie drutu.
Mamy znowu oscylator harmoniczny, modyfikuje się punkt, wokół którego następują
oscylacje. Energia zależy kwadratowo od k, czyli fala częściowo się propaguje wzdłuż osi x.
Wzrost pola powoduje silny wzrost masy.
Położenia będą zależały od prędkości, poszczególne stany rozmieszczone są wzdłuż
krawędzi. W przypadku zmiany prędkości następuje przemieszczenie elektronów na
przeciwną stronę. Elektron nie może ulec rozproszeniu.
Przy w miarę szerokiej próbce potencjał boczny jest równy zeru, a stany krawędziowe
opisane potencjałem. W ten sposób mamy energię zależną od yk. Zmienia się znak prędkości.
Wpływ pola magnetycznego na poziomy Landaua: najpierw zwalniają się stany
zlokalizowane.
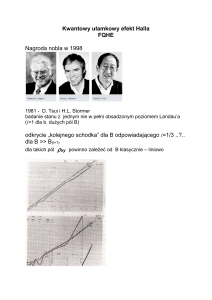
Kwantowy efekt Halla ma te same podstawy, co klasyczny efekt Halla ale występujący w
niższych temperaturach i wyższych polach magnetycznych.
Obniżanie temperatury i zwiększanie pola magnetycznego pozwala zaobserwować:
efekt Shubnikova – de Haasa (oscylacje kwantowe)
całkowity kwantowy efekt Halla
ułamkowy kwantowy efekt Halla
Kwantowy efekt Halla:
obserwowany w niskich temperaturach wyłącznie w układach niskowymiarowych
(dwuwymiarowy gaz elektronowy)
w polu magnetycznym stany elektronowe odpowiadają poziomom Landaua oraz
obecności stanów
16
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
tworzenie się poziomów Landaua oraz obecność stanów zlokalizowanych związanych
z defektami determinują kwantowy efekt Halla
kwantowy efekt Halla polega na przyjmowaniu przez opór elektryczny materiału
h
określonych dyskretnych wartości RH = 2
eM
Elektrony gromadzą się na poziomach Landaua. Istotne jest to, ze mamy domieszki, które
poszerzają poziomy Landauowskie.
Ułamkowy efekt Halla: pik rezystancji jest podłużny, odpowiada on wzrostowi, pojawia się
także plato, które odpowiada za minimum rezystancji. W przypadku silnych pól jeden kwant
wystarczy, żeby na poziomie Landaua osadzić 1/3 elektronu. Układ zachowuje sie jakby
elektron miał ładunek 1/3.
Spinowy efekt Halla: efekt pojawia się w wyniku relatywistycznego sprzężenia spinu z
orbitalnym momentem pędu, gdy elektron porusza się w zewnętrznym polu elektrycznym.
KROPKI KWANTOWE
Kropki kwantowe to układy quasi-zerowymiarowe o wymiarach rzędu długości fali de
Broglie’a i dyskretnych poziomach energetycznych. Kropki istotne z punktu widzenia
transportu to kropki wytwarzane elektrostatycznie.
Kropki pionowe: transport odbywa się w kierunku pionowym, otrzymywane są głównie
litograficznie. Wprowadza się wokół kropki bramkę ściskającą elektrony. W przypadku
kropek istotną rolę odgrywa boczny potencjał.
Aby układ działał jako kropka, odległości między poziomami musza być większe od kT.
Typowe kropki półprzewodnikowe wytworzone są z GaAs w niskich temperaturach.
Kropki o symetrii cylindrycznej: otrzymane w wyniku wprowadzenia pola magnetycznego
skierowanego wzdłuż osi z.
17
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
KROPKI KWANTOWE.
wykład VIII
Kropki o symetrii cylindrycznej: energia E określona przez liczby kwantowe, podobnie jak
dla atomu, l przyjmuje wartości niezależne od n, n zaczyna się od zera - inaczej niż w atomie,
gdzie zaczyna się od 1. W polu będziemy rozszczepiać stany, przy l ujemnym energia w polu
będzie rosłą i na odwrót.
Wpływ pola magnetycznego: w efekcie pojawienia się pola magnetycznego następuje
ściśnięcie elektronów. Pole prowadzi do silnej lokalizacji.
Kropki pionowe. Mamy dyskretne poziomy energetyczne. Takie kropki nazywamy
sztucznymi atomami ze względu na podobieństwo do budowy atomu, tylko, że występuje w
nich symetria cylindryczna zamiast sferycznej. Pierwsza powłoka jak w helu.
Liczby magiczne – liczba elektronów wynikająca z obecności potencjału wiążącego.
Quasiatomy: atom charakteryzuje się: dyskretnymi poziomami energetycznymi, energią
jonizacji (13,6 EV dla wodoru) i powinowactwem elektronowym. Kropki kwantowe spełniają
te warunki i stanowią układy quasiatomowe.
Odziaływania Culombowskie na kropkach – TRANSPORT
Kropki pionowe to najdogodniejsze obiekty do badań transportu. Kropki planarne należą
do mniej dogodnych ze względu na wyższy potencjał, który ogranicza transport. W kropkach
pionowych łatwo obserwować ilość elektronów biorących udział w transporcie. Podłączamy
elektrody, poziomy obsadzone od poziomów nieobsadzonych są oddzielone przerwą
e2
kulombowską o energii
c
Układy, w których prąd zmienia się o rzędy wielkości w wyniku dodania lub odjęcia jednego
elektronu to jednoelektrodowe tranzystory.
Rozważmy układ w konfiguracji tranzystora: mamy dwie elektrody, źródło i dren.
Przykładamy do bramki napięcie i rozważamy model blokady kulombowskiej. Jeżeli na
bramce pojawia się napięcie Vg, to na kropce będzie QVg.
Q2
2C
gdzie Vg to napięcie między bramką i źródłem, QVg to przyciągające oddziaływanie między
łądunkiem Q a potencjłąem Vg, Q2/2C to odpychające oddziaływanie między elektronami
związanymi w kropce
Energia elektrostatyczna kropki o ładunku Q: E = QVg +
E w funkcji Q to parabola, minimum energii odpowiada -CVg, albo całkowitej wielokrotności
ładunku e. Dodanie lub odejmowanie elektronów prowadzi do wzrostu energii.
18
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Zmieniając napięcie bramkowe zmieniamy liczbę elektronów odpowiadającą minimum.
e2
Dodanie lub zabranie elektronu wiąże się ze zmianą energii o
- taka jest też wartość
2C
przerwy. Warunkiem jest odpowiednio mała pojemność układu, taka, aby móc obserwować
efekt blokady kulombowskiej. Przy pewnym napięciu bramkowym przerwa znika, mamy
wówczas zdegenerowany stan i żadna energia nie jest wymagana, żeby dodać lub usunąć
elektron. Następuje tunelowanie elektronu od źródła do drenu, przewodność jest równa zero.
Po przetunelowaniu znowu pojawia się przerwa.
Dopiero przy pewnym napięciu prąd zaczyna płynąc. W przypadku degeneracji blokada
kulombowska zostaje zniesiona, i pojawia się wysoki pik w przewodności. Piki leżą w ściśle
e
określonym równo odległych miejscach. Zmiana napięcia bramkowego wynosi ∆Vg = , co
c
odpowiada odległości między pikami.
e2
, aby obserwować efekty
c
blokady musimy mieć odpowiednio niską temperaturę, żeby nie zniszczyć efektu.
Jednoelektronowy tranzystor: energia kulombowska to
Idealna blokada kulombowska I = GVd
Pompa jednoelektronowa: jedno z możliwych zastosowań. Mamy elektrody źródła i drenu,
układ bramek. Jedne bramki kontrolują wysokość barier między źródłem, kropką i drenem. W
sposób periodyczny możemy zmieniać wysokość barier, w efekcie otrzymamy cykl. W
jednym cyklu przez kropkę przepływa jeden elektron.
Sztuczne atomy: porównanie teorii i eksperymentu, elektrony tunelują na kropkę, pik to
wejście elektronów, trzeci elektron to już druga powłoka (energia kulombowska i energia
kwantowa).
Wpływ pola magnetycznego B: dla kropek w polu magnetycznym następuje zmiana stanów
orbitalnych elektronów, zmienia liczbę orbitalną l. Pole występuje jako kwant strumienia
magnetycznego. Możemy przy pomocy pola magnetycznego zmieniać orbitalny stan
elektronów w atomie. Dla kropek z dużą powierzchnią wystarczy małe pole. Rozszczepienie
Zeemana w polu jest bardzo małe w wyniku małego czynnika żyromagnetycznego w arsenku
galu.
Każdy poziom rozszczepia się na dwa poziomy na wskutek oddziaływania kulombowskiego.
Zafalowania odpowiadają punktom przecięcia, w których następuje zmiana stanu orbitalnego.
Reguła Hunda: reguła mówiąca, że w atomie, w celu uzyskania najbardziej korzystnego
energetycznie
zapełnienia
orbitali
atomowych,
powinno
być
jak
najwięcej elektronów niesparowanych. Elektrony ulegają sparowaniu po pojedynczym
zapełnieniu wszystkich form przestrzennych danych orbitali danej powłoki elektronowej.
Potencjał elektrochemiczny jest równy różnicy energii układu dla N elektronów i N-1
elektronów.
19
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Kropki mają powłoki obsadzane zgodnie z regułą Hunda.
Charakterystyka I-V. Schody Culomba. W charakterystyce wyraźnie widoczny jest efekt
blokady kulombowskiej. Prąd zaczyna się po pokonaniu blokady przy pomocy zewnętrznego
napięcia. Każdy schodek odpowiada przepływowi elektronu.
Jako kropki mogą być traktowane różne układy, nie tylko kropki półprzewodnikowe, jak
klastery, molekuły np. C60.
Najłatwiej kropki otrzymać w zawiesinach koloidalnych.
Efekty interferencyjne można łatwo obserwować dla układu dwóch kropek kwantowych
połączone ze sobą elektrodami - źródłem i drenem. Możemy zmieniać sprzężenia między
kropką i elektrodą. Fale elektronowa ma różne możliwości przejścia. W tego typu układach
interferencje kwantowe prowadzą do efektu Fano. Zmieniając napięcie bramkowe możemy
przechodzić od minimum do maksimum przewodności, co wynika z interferencji.
20
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
EFEKT KONDO. GRAFEN.
wykład IX
EFEKT KONDO
W niskich temperaturach opór przewodnika jest niemierzalny. Dla metalu z domieszkami
poniżej pewnej temperatury następuje silny wzrost logarytmiczny rezystancji.
Wprowadzamy temperaturę
T
i dla wszystkich materiałów będziemy mieli taką samą
Tk
T
R
= f .
R0
Tk
Silny wzrost rezystancji nosi nazwę efektu Kondo. W celu wyjaśnienia efektu Kondo należy
uwzględnić silne relacje w gazie elektronowym.
zależność (uniwersalne skalowanie)
Ważne, by spin na kropce był różny od zera – wówczas przewodność kropki wzrasta, by w
2e 2
(maksimum wartości) osiągnąć w temperaturze zera bezwzględnego – kropka staje się
h
wówczas całkowicie transparentna, transmisja równa jeden. Efekt Kondo prowadzi do
wzrostu przewodności. Po określeniu temperatury Kondo dla kropek także obserwuje się
T
G
uniwersalne skalowanie
= f .
G0
Tk
Model Andersona: wyjaśnia efekt Kondo zarówno dla domieszki magnetycznej jak i kropki
kwantowej. Energia układu musiałaby bardzo silnie wzrosnąć, żeby na kropkę o spinie do
góry wprowadzić elektron o innym spinie. Efekt Kondo obserwuje się tylko, gdy poziom
kropek leży znacznie poniżej poziomu Fermiego obu elektrod.
W modelu Andersona można określić temperaturę Kondo TK =
1 Πε
1
(ΓU )2 e 0
2
ε 0 +U
ΓU
Istniej możliwość zajścia wirtualnego tunelowania – wówczas elektron o spinie do góry
może przejść do elektrody, ale wirtualnie – w bardzo krótkim okresie czasu, niespełniona
zasada zachowania energii ∆E ⋅ ∆t ∝ h
Tunelowanie można opisać przez parametr Γ. W efekcie wirtualnego tunelowania końcowy
stan jest taki, jakby elektron przetunelował przez układ. Następuje zmiana spinu na kropce.
Pojawia się wysoki pik - pik Kondo - w gęstości stanów. Szerokość piku jest rzędu
temperatury Kondo.
W efekcie pojawienia się piku Kondo kropka staje się transparentna, duża konduktancja.
Duża gęstość stanów powoduje zwiększenie prawdopodobieństwa tunelowania dla kropki.
21
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Silne rozpraszanie elektronu prowadzi do wzrostu rezystancji. Im więcej elektronów w
pobliżu poziomu Fermiego, tym silniejsze rozpraszanie.
Temperatura Kondo opisana jest charakterystycznymi parametrami, które można
modulować dla kropek: wielkością sprzężenia między elektrodami a kropką, potencjałem
charakteryzującym tunelowanie, energią kulombowską i przez napięcie bramkowe
zmieniające ε0.
Zmieniając napięcie bramkowe zmienia się liczbę elektronów na kropce. Gdy temperatura
maleje, to przewodność kropki maleje. Gdy liczba elektronów jest nieparzysta (wypadkowy
2e 2
spin 1/2), to temperatura maleje i przewodność rośnie aż do maksimum
i mamy wyraźne
h
plato odpowiadające efektowi Kondo.
Dla niskich temperatur pik Kondo jest wysoki, ale ze wzrostem temperatury poszerza się i w
końcu znika w temperaturach wyższych.
Pik Kondo rozszczepia się po przyłożeniu napięcia źródło – dren na dwa piki stowarzyszone
z prawą i lewą elektrodą. Im silniejsze sprzężenie, tym rozszczepienie piku Kondo będzie
większe. Temperatura nie wpływa na gęstość stanów, tylko na pik Kondo.
Po wprowadzeniu pola także nastąpi rozszczepianie na dwa piki, na wskutek rozszczepiania
poziomu kropki. Duże pole całkiem niszczy efekt Kondo.
Umieszczenie kropki z niezerowym momentem spinowym między dwiema elektrodami
ferromagnetycznymi. Gdy momenty elektrod są antyrównoległe, od elektrod nie pochodzi
żadne pole, gdy konfiguracja równoległa, nastąpi rozszczepienie poziomu kropki na dwa
poziomy w efekcie działania pola pochodzącego od elektrod.
W konfiguracji równoległej piki Kondo się rozszczepią, nie ma za to rozszczepienia w
konfiguracji antyrównoległej, bo pola się znoszą. Dodanie napięcia spowoduje rozszczepienie
każdego z pików na dwa.
Eksperyment z molekułą C60 podłączoną do elektrod. Po naniesieniu na elektrody ze złota
elektrod z niklu dużo mniejsze pole jest potrzebne do uzyskania rozszczepionego piku Kondo.
Molekularny tranzystor: między dwiema elektrodami umieszczona zostaje molekuła z
dwoma atomami wanadu. Na wykresie pojawiają się Diamenty Kulomba: linie, wzdłuż
których następuje zwyczajny transport elektronowy. Po lewej stronie wystąpi pik Kondo, po
prawej nie, z powodu blokady kulombowskiej. Efekt Kondo jest silnie sprzężony ze
spinem.
Bardzo silne pola są potrzebne, aby doprowadzić do rozszczepienia piku w niemagnetycznym
materiale.
22
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
GRAFEN
Grafen: układ dwuwymiarowy, pierwszy dwuwymiarowy kryształ, który został otrzymany, o
szczególnych właściwościach. Twierdzenie Mermina-Wagnera mówi, że w układach
niskowymiarowych nie możemy mieć jakiegokolwiek uporządkowania dalekiego zasięgu.
Jeżeli wytworzymy warstwę 2D, to taka warstwa ma zawsze skończone wymiary. Kryształ
2D najczęściej nakłada się na podłoże w postaci pojedynczej warstwy, więc w sumie jest to
układ 3D. W rezultacie twierdzenie Mermina-Wagnera, ani inne twierdzenia nie będą miały w
pełni zastosowania.
Otrzymywanie grafenu: zaczynamy od idealnie czystego grafitu, wobec którego stosujemy
eksfoliację - wyłuskiwanie pojedynczych warstw mechanicznie albo chemicznie. Uzyskane
warstwy nakładanie najczęściej na podłoże swobodne.
Charakterystyczne dla grafenu są: szczególna struktura pasmowa, w punktach k, w
wierzchołku strefy Brillouina energia równa zeru, struktura pasmowa w pobliżu punktu
Diraca liniowa, co jest konsekwencją liniowej relacji dyspepsji, dającej idealną symetrię
elektron – dziura. Grafen zawiera w komórce elementarnej dwa atomy: jakby dwie identyczne
podsieci, stąd funkcja falowa dla grafenu może być przedstawiona w postaci
ΨA
dwuwymiarowego spinora: Ψ = gdzie ΨA ,ΨB to funkcje falowe dla podsieci A i B.
ΨB
Spinor związany jest z amplitudą funkcji falowej, a nie ze spinem. Funkcja falowa dla spinu
Ψ
Ψ = 1 też ma znaczenie w grafenie. Ze względu na spinor mówimy o pseudospinie.
Ψ2
Metody otrzymywania grafenu:
- eksfoliacja: chemiczna – traktowanie grafitu kwasami, daje grafen wysokiej jakości o ile
grafit był wysokiej jakości; mechaniczna – metoda Scotcha
- epitaksjalna
- CVD
Metoda Scotcha: potrzebne podłoże, taśma klejąca, grafit nanosimy na taśmę, podłoże musi
spełniać warunek adhezji, najlepsze podłoże SiO2.
Epitaksjalne otrzymywanie grafenu: wzrost warstw na podłożu.
Metoda chemiczna CVD: wykorzystuje dysocjujący CH4, może otrzymywać duże warstwy
grafenu, ale o niższej jakości, problemem jest przeniesienie z metalu na izolująca folię.
Inne dwuwymiarowe kryształy: azotek boru, selenek niobu, siarczek molibdenu.
Najbardziej zbliżona do grafenu sieć (heksagonalną płaską) ma azotku boru - półprzewodnik
o stosunkowo szerokiej przerwie w odróżnieniu od grafenu mającego zerową przerwę
energetyczną.
Graphane: grafen z wodorem, graFane – grafen z fluorem. W obydwu pojawia się przerwa
energetyczna. Obecność wodoru prowadzi do dużych zmian przewodności. W czystym
grafenie zmieniając napięcie bramkowe zmieniamy koncentrację elektronów i dziur, dla
grafenu z wodorem inna zależność, wrażliwa na temperaturę rezystancja, podobnie dla fluoru.
23
NANOSTRUKTURY 2012
-------------------------------------------------------------------------------------------------------------------------------------------------------
Otrzymywanie pasków grafenowych: wprowadzenie wodoru w odpowiedni sposób albo
trawienie – obydwie metody to złożone, trudne procesy. Paski grafenowe mają ciekawe
właściwości, mogą być metaliczne, albo półprzewodnikowe.
Moment magnetyczny w grafenie: w grafenie występuje topologiczny magnetyzm,
charakterystyczny dla pasków grafenowych typu zig-zak. Moment magnetyczny lokalizuje się
na brzegach paska.
Sieć odwrotna
Struktura pasmowa
cA, cB – amplitudy, różnią się fazą eiθ , tu faza związana wyłącznie z topologią, położeniem
atom A lub B. W punktach k i k’ mamy różną topologię, fazy są różne, co jest związane z
pseudospinem, dodatkową symetrią w grafenie.
Jeżeli znajdziemy się w pobliżu k, rozwijamy w pobliżu k energię w szereg. Hamiltonian
→ →
można zapisać w postaci macierzowej, a hamiltonian w pobliżu punktu k vF σ ⋅ k - postać
charakterystyczna dla bezmasowych, relatywistycznych cząstek. W pobliżu punktu k cząstki
będą się zachowywały jak cząstki relatywistyczne.
1
1
En = hω0 N + ρ xy = 2
e
2
N
h
∆ELL – odległość między poziomami landauowskimi, c* - efektywna prędkość światła
24