SIECI NEURONOWE
WYKORZYSTANIE DO PROGNOZOWANIA WIG
Dr Kamila Migdał Najman
Dr Krzysztof Najman
Katedra Statystyku
Wydział Zarządzania
Uniwersytet Gdański
[email protected]
[email protected]
SOPOT styczeń – grudzień 2000
Ostatnia dekada XX wieku cechuje się niezwykle dynamicznym rozwojem nauki nad sztuczną
inteligencją obejmującą swoją tematyką sieci neuronowe, systemy rozmyte i algorytmy genetyczne.
Jest to wynikiem szybkiego rozwoju technologii w dziedzinie komputerów osobistych oraz
komputerów o wielkiej mocy obliczeniowej, co umożliwia naukowcom symulowanie i testowanie
nowych idei w sposób nie możliwy przed rokiem 1980. Źródłem inspiracji sztucznych sieci
neuronowych jest biologia układów nerwowych. Wszystkie żywe istoty posiadają mózgi złożone z
komórek zwanych neuronami. Szacuje się, że mózg ludzki może składać się nawet ze 100 miliardów
neuronów. Mózg człowieka ma przewagę nad komputerem w wielu zadaniach. Jest odporny na
uszkodzenia. Mimo, że codziennie obumiera wiele komórek nerwowych nie ma to znacznego wpływu
na pojemność i funkcjonowanie mózgu. Jest elastyczny. Może się z łatwością przystosować do
zmiennego otoczenia przez „uczenie się”. Potrafi sobie radzić z informacją rozmytą, losową,
zaszumioną lub niespójną. Jest w wysokim stopniu równoległy. Jest mały, zwarty i zużywa bardzo
mało energii. Komputer przewyższa mózg tylko w zadaniach opartych na prostych operacjach
arytmetycznych. Czasami mówi się, że komputer to bardzo szybki „idiota”, który znajduje rozwiązania
zadanych problemów jedynie dzięki błyskawicznej analizie tysięcy prawdopodobnych przypadków.
Sieci neuronowe wyrosły z badań prowadzonych nad sztuczną inteligencją. Próbują one naśladować
wysoką tolerancję na uszkodzenia i zdolność samouczenia biologicznego systemu neuronowego. W
wielu przypadkach stały się one podstawą zastosowania w nietypowych ( z biologicznego punktu
widzenia ) dziedzinach jak finanse, inżynieria, geologia czy fizyka. Faktycznie, gdziekolwiek pojawia
się problem predykcji, klasyfikacji lub kontroli, sieci neuronowe są brane pod uwagę jako
alternatywne do innych metod analitycznych. Często osiąga się znakomite rezultaty. Ten sukces może
być przypisany pewnym kluczowym czynnikom jak : odporność i zdolność uczenia. Sieci neuronowe
są skomplikowaną techniką modelowania, zdolną do modelowania niezmiernie złożonych systemów.
Można je traktować jako nowoczesne systemy obliczeniowe, które przetwarzają informacje wzorując
się na zjawiskach zachodzących w mózgu człowieka. Informacje jednak mają tu charakter danych
numerycznych. Sieć neuronowa działa na matematycznych zbiorach danych (wektorach, macierzach),
które przybierają postać określonych porcji informacji. W odróżnieniu od mózgu, gdzie dane
wejściowe są odbierane za pośrednictwem pięciu zmysłów, sztuczne sieci neuronowe odbierają dane
wejściowe za pomocą liczb. W wielu zastosowaniach sztucznych sieci neuronowych operują one
jedynie zerami i jedynkami, które oznaczają, że dana zmienna jest obecna lub nie. W praktyce,
sztuczna sieć neuronowa ( SN ) to program komputerowy, który naśladuje zdolność ludzkiego mózgu
do klasyfikacji, rozpoznawania wzorców, analizy i kompresji obrazów, sporządzania prognoz lub
podejmowania decyzji na bazie przeszłych doświadczeń. SN to bardzo uproszczony model mózgu
składający się z dużej liczby elementów przetwarzających informację. Elementy nazywane są
neuronami, chociaż w stosunku do rzeczywistych komórek nerwowych ich funkcje są bardzo
uproszczone. Topologia połączeń oraz ich parametry stanowią program działania sieci, zaś sygnały
pojawiające się na jej wyjściach w odpowiedzi na określone sygnały wejściowe są rozwiązaniami
stawianych jej zadań.
Rozmaitość SN badanych obecnie jest ogromna. Poszczególne neurony można modelować jako
proste sumatory ważone, złożone układy równań różniczkowych lub dowolne modele pośrednie.
Połączenia między neuronami mogą być zorganizowane w warstwy tak, aby informacje przepływały
tylko w jednym kierunku, albo tak, aby mogły krążyć po całej sieci w sposób cykliczny. Wszystkie
neurony mogą zmieniać stan jednocześnie albo też można wprowadzić opóźnienia. Wszystkie
odpowiedzi mogą być ściśle deterministyczne albo dopuszcza się zachowanie przypadkowe. Warianty
można mnożyć...
SN bywają na ogół lepsze od innych metod analitycznych przy spełnieniu następujących warunków:
1. Dane, z których trzeba wyciągną wnioski są „rozmyte”. Jeżeli danymi wejściowymi są ludzkie
opinie, źle określone kategorie lub dane są obarczone dość dużymi błędami, to odporne
zachowanie sieci neuronowych jest ich ważną zaletą.
2. Jedną z głównych zalet sieci neuronowej jest jej zdolność do odkrywanie w zbiorze danych
wzorców, które są tak niejasne, że są niewykrywalne przez zmysły badaczy i przez tradycyjne
metody statystyczne. Np. przewidywanie wypłacalności pożyczkobiorców na podstawie historii
ich wydatków i wpływów. Wykazano, że SN lepiej „podejmują decyzje” niż doświadczony
personel.
3. Dane wykazują znaczną, nieoczekiwaną nieliniowość. SN mają bardzo duże zdolności
adaptacyjne.
4. Dane są chaotyczne. Chaos można wykryć w wahaniach cen na giełdzie. Takie zachowanie nie
daje szans większości innych metod, ale SN są na ogół odporne na sygnały wejściowe tego
rodzaju.
SN nie ma sensu stosować gdy są znane dokładne, klasyczne (deterministyczne) rozwiązania badanych
problemów. Wówczas włożony w budowę sieci trud się nie opłaci. Uzyskamy bowiem, co najwyżej,
identyczne rezultaty jak w metodach klasycznych. Wiele SN odznacza się zarówno mocnymi
podstawami teoretycznymi, jak i użytecznością w praktyce. Wadą SN jest to, że w porównaniu z
ludzkim mózgiem, który składa się z miliardów neuronów, sieć ma ich zaledwie kilkaset. Sieć
mechanicznie rozwiązuje tylko zadane problemy, i to tylko jedno zadanie w danym czasie. Można,
więc raczej mówić o specjalizacji SN. Tak więc buduje się różne sieci dla różnych zastosowań.
Dziedziny finansów, w których na szeroką skalę stosuje się sieci neuronowe, to:
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
9
Oszustwa związane z kartami kredytowymi
Prognozowanie bankructw
Analiza wniosków o udzielenie pożyczki hipotecznej
Marketing produktu
Klasyfikacji obligacji przedsiębiorstw
Prognozowanie zachowania rynku akcji
Prognozowanie upadłości banków
Selekcja akcji
Wycena nieruchomości
Wycena arbitrażowa
Analiza kondycji finansowej przedsiębiorstw
Wycena opcji
Wybór strategii sprzedaży
Prognozowanie sprzedaży
Podejmowanie decyzji na szczeblu menedżerskim
Analiza kondycji biur turystycznych
Prognozowanie wskaźników ekonomicznych
Przewidywanie przepływów gotówkowych
Lokalizowanie podmiotów uchylających się od płacenia podatków
Wybór funduszu powierniczego
Dodatkowym atutem SN jest wygoda ich programowania poprzez uczenie. Zamiast projektować
algorytm wymaganego przetwarzania informacji i dzielić go na moduły nadające się do współbieżnego
wykonywania - stawia się sieci przykładowe zadania i automatycznie, zgodnie z założoną strategią
uczenia modyfikuje się połączenia elementów sieci ich współczynniki wagowe. W ten sposób sieć
programuje się sama, co czasem prowadzi do rozwiązań w bardzo krótkim czasie, a innym razem
może wymagać tysięcy iteracji Zawsze jednak przebiega w sposób samoczynny, a więc nie
absorbujący dla człowieka poszukującego określonych rozwiązań.1 Większość współcześnie
budowanych sieci neuronowych ma budowę warstwową, przy czym ze względu na dostępność w
trakcie procesu uczenia wyróżnia się warstwy: wejściową, wyjściową oraz tak zwane warstwy ukryte.2
1
2
Ryszard Tadeusiewicz, Sieci neuronowe, Akademicka Oficyna Wydawnicza, Warszawa 1993, s. 19
tamże, s. 12-13
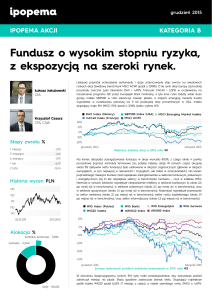
Rys.1
Na rys.1 przedstawiono przykładową strukturę sieci neuronowej budowaną dla potrzeb prognozowania
WIG’u na podstawie przeszłych notowań. 80% wszystkich zastosowań sieci neuronowych dotyczy
tzw. sieci wielowarstwowych, które charakteryzują się brakiem sprzężeń zwrotnych. Przesyłają one
sygnały od warstwy wejściowej, poprzez warstwy ukryte (jeśli występują), do warstwy wyjściowej.
Składają się one z trzech bądź większej liczby warstw neuronów. Pierwsza warstwa, określana
mianem warstwy wejściowej, zawiera tyle neuronów, ile jest zmiennych wejściowych. Te wejścia są
zazwyczaj nazywane neuronami wejściowymi, które dają sygnały wejściowe. Warstwa ta otrzymuje
dane z zewnątrz sieci. Każdy neuron z warstwy wejściowej łączy się ze wszystkimi neuronami z
obszaru ukrytego. Obszar ukryty składa się niekiedy z więcej niż jednej warstwy; każdy neuron z
pierwszej warstwy ukrytej powiązany jest wówczas ze wszystkimi neuronami warstwy drugiej. Jeżeli
obszar ukryty składa się więcej niż dwóch warstw, neurony z drugiej warstwy łączą się ze wszystkimi
neuronami z warstwy trzeciej. Najkrócej można powiedzieć, że warstwy te stanowią narzędzie, służące
do takiego przetwarzania sygnałów wejściowych, by warstwa wyjściowa mogła łatwiej znaleźć
potrzebną odpowiedź. Działanie neuronów warstw pośrednich nie jest bezpośrednio widoczne dla
użytkownika sieci – w tym sensie można mówić, że są one ukryte. Neurony warstwy ukrytej pełnią
rolę pośredników. Pośredniczą między wejściem i wyjściem oraz wypracowują zestawy wstępnie
przetworzonych danych wejściowych, z których korzystać będą neurony dalszych warstw przy
określeniu końcowego wyniku. Ostatnia warstwa wchodząca w skład obszaru ukrytego połączona jest
z warstwą wyjściową. Istnieje także jeden lub więcej neuronów wyjściowych. Dzięki nim
otrzymujemy wynik działania sieci. Każdy neuron wyjściowy przyjmuje sygnały wejściowe,
przetwarza je i wytwarza sygnał wyjściowy. Sygnały te stanowią rozwiązania stawianych sieci zadań.
Jak to się dzieje, że sieć zdobywa i gromadzi wiedzę? To siła powiązań między różnymi neuronami
sprawia, że na pozór identyczne sieci różnią się od siebie. Siłę powiązań między dwoma neuronami
określa się mianem wagi. Mocne powiązanie ma większą wagę niż słabe. Ważne zmienne wejściowe
otrzymują duże wartości wag. Wyrażają stopień ważności informacji docierających wejściem. Gdy
waga jest większa od 1 to sygnał wchodzący określonym wejściem jest wzmocniony, gdy waga ma
wartość mniejszą od 1 to sygnał jest stłumiony bądź też można mówić o wejściu hamującym, gdy
waga ma wartość ujemną. Neurony są powiązane w sieć za pomocą połączeń ( wag ) modyfikowanych
w trakcie uczenia. Każdy neuron ma wiele wejść, za pomocą których odbiera sygnały od innych
neuronów oraz sygnały wejściowe podawane do sieci jako dane do obliczeń. Cała sztuka polega na
tym aby tak dobrać wagi, aby wszystkie neurony wykonywały dokładnie takie czynności, jakich się od
nich wymaga. W sieci jest jednak tyle neuronów, że nie jesteśmy w stanie dla wszystkich wejść
zdefiniować potrzebnych wag. Możemy jednak rozpocząć działanie sieci z przypadkowym zestawem
wag i stopniowo polepszać te wagi. Neuron sam potrafi określić, które ze swoich wag ma zmienić, w
którą stronę i o ile. Proces zmiany wag przebiega w każdym neuronie sieci w sposób spontaniczny i
niezależny. Proces uczenia może być powadzony równocześnie we wszystkich neuronach sieci.
Pewne elementy w sieci neuronowej są zdeterminowane. Między innymi liczba elementów
wejściowych i wyjściowych oraz zasada połączeń między kolejnymi warstwami. Są jednak elementy
zmienne, które trzeba określić samemu: liczbę warstw ukrytych (jedna czy kilka) oraz liczbę
elementów warstwie (warstwach) ukrytych. Elementy te ustala się zwykle arbitralnie. Nie można
jednak zaprojektować sieci o zbyt małej liczbie elementów. Jeżeli występuje za mało neuronów,
proces uczenia może się definitywnie nie udać, gdyż sieć nie ma szans odwzorować w swojej
strukturze wszystkich niuansów rozwiązywanego zadania. Nie można także "przedobrzyć"
Zastosowanie zbyt wielu warstw ukrytych prowadzi do znacznego pogorszenia sprawności procesu
uczenia, dlatego często lepsze wyniki dale sieć o mniejszej liczbie warstw ukrytych niż sieć z większą
liczbą warstw ukrytych. Również ustalenie nadmiernej liczby neuronów w warstwie ukrytej prowadzi
do niekorzystnego efektu nazywanego "uczeniem się na pamięć". Sieć w ten sposób zamiast
uogólniania nabywanych wiadomości dokonuje zapamiętania reguł.
Cykl działania sieci neuronowej podzielić można na etap nauki, kiedy sieć gromadzi
informacje potrzebne jej do określenia, co i jak ma robić, oraz na etap normalnego działania,
nazywany czasem egzaminem, kiedy w oparciu o zdobytą wiedzę sieć musi rozwiązywać konkretne
nowe zadania.
Sieć neuronowa uczy się na dwa sposoby. Najczęstsze jest uczenie pod nadzorem. Polega na
tym, że sieci podaje się przykłady poprawnego działania, które powinna ona potem naśladować w
swoim bieżącym działaniu. Zbieramy wiele próbek, które odgrywają rolę przykładów. Każda próbka
zbioru uczącego całkowicie określa wszystkie wejścia, jak również wyjścia wymagane przy
prezentacji tych danych wejściowych. Następnie wybieramy podzbiór zbioru uczącego po kolei i
podajemy próbki z tego podzbioru na wejście sieci. Dla każdej próbki porównujemy aktualny sygnał
wejściowy sieci z sygnałem wyjściowym, który chcielibyśmy otrzymać. Po przetworzeniu całego
podzbioru próbek uczących korygujemy wagi łączące neurony w sieci w celu zmniejszenia miary
błędu działania sieci. Jedna prezentacja podzbioru próbek uczących wraz z odpowiednią korekcją wag
jest nazywana EPOKĄ. Liczba próbek podzbioru jest nazywana rozmiarem epoki. Epoki uczenia
powtarzamy aż do osiągnięcia zadawalającej jakości przetwarzania sieci. Inną podstawową metodą
uczenia jest uczenie bez nadzoru. Proces uczenia sieci polega na wykryciu istotnych cech zbioru
uczącego i wykorzystaniu ich do grupowania sygnałów wejściowych na klasy, które sieć potrafi
rozróżniać. Sieć potrafi wykorzystać same obserwacje wejściowe i zbudować na ich podstawie
algorytm działania, automatycznie wykrywający klasy powtarzających się sygnałów wejściowych i
rozpoznawać te typowe wzorce sygnałów. Proces sprawdzania użyteczności sieci nazywamy
weryfikacją. Proces taki polega na rozdzieleniu zbioru znanych przypadków na dwa zbiory rozłączne.
Jeden to zbiór uczący, wykorzystywany do uczenia sieci. Drugi to zbiór testowy, używany do
egzaminowania sieci po zakończeniu uczenia.
Uczenie i stosowanie sieci wymaga postępowania według etapów:
1. Określenie prognozowanej zmiennej.
2. Gromadzenie zbiorów danych lub szeregów czasowych związanych z prognozowanym
zjawiskiem,
3. Wstępne przetwarzanie danych tak, aby łączyły informacje lub przedstawiały je w bardziej
użyteczny sposób ( skalowanie, normalizacja, standaryzacja, zmniejszanie wymiarowości
problemu).
4. Wyodrębnienie uczącego i testowego zbioru danych, czyli danych do jej uczenia i do
przyszłego testowania.
5. Wybór odpowiedniej architektury sieci. Ustalenie liczby warstw, liczby neuronów w
warstwach ukrytych.
6. Wybór odpowiedniego algorytmu uczenia (treningowego) i ustalenie jego parametrów.
7. Uczenie sieci.
8. Weryfikacja jakości nauczonej sieci.
9. Zastosowanie sieci. Do nauczonej sieci wczytujemy nowe zbiory danych lub dane bieżące w
celu otrzymania prognozy czy dokonania klasyfikacji.3
Jeżeli przestrzegamy powyższych zasad i mamy trochę szczęścia uda nam się zbudować poprawnie
działającą sieć.
BADANIA EMPIRYCZNE
Badania empiryczne zastosowań sieci neuronowych na rynkach kapitałowych są prowadzone
od bardzo dawna. Zwykle budując model do celów prognostycznych możemy zastosować dwa
podejścia. Pierwsze to podejście autoregresyjne. Oznacza to, że badany proces będziemy modelowali
jedynie na podstawie jego własnych opóźnień. A więc prognozujemy WIG jedynie na podstawie
przeszłych notowań WIG’u. Drugie podejście to wprowadzenie do modelowania dodatkowych
zmiennych objaśniających np. wartości wskaźników technicznych. W dalszej części rozpatrzymy oba
przypadki.
PROGNOZOWANIE KIERUNKU ZMIAN WIG
Dobrym wstępem do badań nad możliwościami zastosowania SN na WGPW jest próba
prognozowania kierunku zmian WIG'u. Jest to z pewnością informacja wielce pożądana. Spróbujmy
więc zbudować prognozę kierunku zmian na następną sesję. Danymi wejściowymi będą notowania
WIG z poprzednich sesji. Liczba notowań, które trzeba uwzględnić jest osobnym problemem i
powinna być optymalizowana. Dane należy przegotować tak aby były one dogodne dla wybranego
typu sieci. W przeciwieństwie do Gateley’a uważamy, że nie należy stosować wartości –1 i 1 czy 0 i 1
dla oznaczania wzrostu i spadku w sieciach warstwowych uczonych algorytmem propagacji wstecznej.
Funkcje aktywacji: logistyczna czy tangens hiperboliczny nie mogą bowiem osiągnąć takich skrajnych
wartości. Skutkuje to zwykle tym, że sieć nie nauczy się badanego problemu. Dla problemu
klasyfikacyjnego, za jaki można uznać tego typu prognozę, proponujemy wykorzystać sieć
probabilistyczną. Dane przygotowujemy więc następująco: sesja wzrostowa: klasa 1, sesja spadkowa:
klasa 2. Sesji o identycznych kolejnych wartościach WIG można nie uwzględnić. W całej historii
WGPW było ich nieistotnie mało. Analizie poddajemy 1000 próbek począwszy od 3514 sesji.
Ponieważ nie wiadomo z góry ile opóźnień uwzględnić w próbce uczącej znajdziemy ją
doświadczalnie. Rozpoczniemy od uwzględnienia jedynie notować „wczorajszych” a zakończymy
biorąc pod uwagę 200 poprzednich sesji. Prognozujemy zmiany kierunku WIG dla kolejnych 20 sesji.
SN na wyjściu poda nam czy „jej zdaniem” następna sesja będzie wzrostowa czy spadkowa. Nie
3
Na podstawie: Ed Gately, Sieci neuronowe. Prognozowanie finansowe i projektowanie systemów transakcyjnych,
Warszawa1999, WIG – Press, s. 9-11
4
Pomijamy 350 pierwszych sesji „szalonej hossy”.
powinno się ustalać poziomów braku wyraźnego sygnału. Jest to bowiem trzeci wariant odpowiedzi,
którego sieć się nie uczyła. Takie poziomy są zresztą zawsze subiektywne5 i bardzo ryzykowne.
Rys.2 ( 180 minut pracy komputera6)
Widać, że najlepsze prognozy popełniały 25% błędów. Takie wyniki uzyskiwały sieci o 100,
108 i 172 uwzględnionych opóźnieniach WIG’u. Zdając się na ślepy los mielibyśmy 50% szans na
wskazanie prawidłowego kierunku zmian. SN pozwoliła nam zyskać dodatkowe 25%. Tu ważna
uwaga. Pamiętać należy, że sieć uczy się na przykładach. Jeżeli obserwujemy istotne zmiany
jakościowe w kształtowaniu się prognozowanego szeregu w stosunku do przeszłości to nie
wymagajmy od SN aby potrafiła je trafnie klasyfikować. W sytuacji takiej należy sieć wytrenować na
nowym – poszerzonym zbiorze danych. W praktyce warto to zrobić raz na miesiąc ( czyli po ok. 20
sesjach ). Nie ma więc sensu badanie zdolności SN w dłuższym horyzoncie czasowym – daleko
wybiegającym poza okres uwzględniony w zbiorze danych uczących. Jest to jedna z przyczyn dla
której gotowe oprogramowanie budujące strategie inwestycyjne na bazie SN najpierw sprawdza się
później nie, następnie znowu działa dobrze itd. ...
Bardzo przydatna dla inwestora może być informacja o spodziewanym kierunku zmian na
rynku w najbliższym tygodniu. Spróbujemy więc zrobić prognozę na najbliższy tydzień. Jest to miara
bardzo ogólna wyrażająca jedynie „skłonności” rynku. Poszukiwania optymalnej sieci rozpoczniemy
od przygotowania danych. W tym konkretnie celu możliwe są dwa podejścia. Po pierwsze możemy
robić prognozy średniej wartości WIG na następny tydzień lub na następne 5 sesji. Różnica jest
5
6
Więcej szczegółów: T.Masters, ‘Sieci neuronowe w praktyce”, WNT W-wa 1996, rozdział 10.
Wszystkie testy były wykonywane na następującym zestawie komputerowym:
ATHLON 650, 265 Mb RAM, MatLab 5.3.1 + Neural Network Toolbox 3.0.1.
istotna. W pierwszym przypadku wyznaczamy średnie wartości WIG dla każdego tygodnia. W drugim
przypadku wyznaczamy średnie 5-cio sesyjne. Należy zwrócić uwagę, że posługując się średnimi
możemy znacznie skrócić liczbę dostępnych próbek uczących i testowych. Gdybyśmy szacowali
średnie tygodniowe to próbek będzie tyle co tygodni a więc liczba danych zmniejszy się pięciokrotnie
! Przy średnich 5-cio sesyjnych strata będzie równa 4 sesje a więc nieistotnie mało. My skupimy się tu
na tym pierwszym podejściu. Postaramy się zrobić prognozy średniego poziomu WIG’u na kolejny
tydzień. Optymalizację przeprowadzamy podobnie jak poprzednio. Ze względu na znacznie mniejszy
zbiór danych uczącym maksymalnie udało się uwzględnić 120 opóźnień. Próba ucząca liczyła 200
tygodni. Prognozy były szacowane na kolejnych 10 tygodni.
RYS. 3 ( 120 minut pracy komputera )
Na rysunku 3 widzimy procent błędów jaki popełniały budowane sieci przy prognozach kierunku
zmian przeciętnego tygodniowego poziomu WIG’u. Udało się zbudować kilkanaście sieci
popełniających jedynie 10% błędów. Jedna sieć o 14 opóźnieniach nie popełniła ani jednego błędu na
przestrzeni 10 tygodni ! Analogicznie jak poprzednio należy co ok. 10 tygodni wytrenować sieć
ponownie.
PROGNOZOWANIE WARTOŚCI WIG
Drugim, obok prognoz kierunku zmian, jest problem prognozowania wartości badanego
waloru. Jest to uzupełnienie powyższych analiz o wskaźnik skali zmian. Staramy się nie tylko ustalić
kierunek zmian ale i ich wielkość. Jest to zadanie dużo trudniejsze ze względu na wymaganą wysoką
precyzję. Przeciętne zmiany WIG w badanym okresie wynosiły średnio 190 punktów z sesji na sesję (
co do wartości bezwzględnej ). Rozproszenie tych zmian wyniosło 287 punktów. Gdyby wyrazić te
wartości w procentach byłoby to odpowiednio : 1.28% i 2.01 %. Aby prognozy miały istotną wartość
to błędy w dłuższych okresach powinny być mniejsze niż 1% z mniejszym niż 2% rozproszeniem ! Jak
widać już z tego powodu jest to zadanie bardzo trudne.
Analizy poprowadzimy w następujący sposób. Budujemy sieć (RYS.1) w oparciu o wartości
WIG z poprzednich sesji. Optymalna liczba uwzględnionych opóźnień będzie wyznaczona
eksperymentalnie. Będziemy jej poszukiwać uwzględniając kolejno od 1 do 50-ciu opóźnień. Tym
razem zastosujemy sieć jednokierunkową, bez sprzężeń zwrotnych z jedną warstwą ukrytą. Jako
algorytm uczący zastosujemy propagację wsteczną w szybko zbieżnej wersji Lavenberga –
Marquardta. Ponieważ WIG przyjmuje jedynie wartości dodatnie, dane przeskalujemu do przedziału
(0,1) Ponieważ wszystkie wartości są dodatnie wybierzemy funkcję aktywacji logistyczną. Liczbę
neuronów ustalamy na pierwiastek kwadratowy z liczby danych wejściowych. Liczbę tą możemy
zwiększyć gdyby nie udało się uzyskać zadowalających wyników. Krok uczenia ustalamy na 0.02,
maksymalny czas uczenia pojedynczej sieci na 15 minut, maksymalną liczbę epok na 507. Sieć
uczymy na 1000 próbek. Prognozy wykonujemy na 50 kolejnych sesji. Każdą próbę uczenia i prognoz
powtarzamy 10 razy. Jest to niezbędne, ponieważ sieć rozpoczyna naukę od losowych wartości wag.
Jedne kombinacje będą ”szczęśliwsze” inne mniej. Kolejne rysunki wyjaśnią to dokładnie.
RYS. 4 ( 50 minut pracy komputera)
7
Liczba ta wydaje się śmiesznie niska. Jednak w każdym z prezentowanych eksperymentów była ona wystarczająca do
osiągnięcia zakładanej dokładności lub najwyższej zdolności do generalizacji sieci.
Rysunek 4 ukazuje zależności między liczbę danych wejściowych a MAPE8. Niebieskie słupki
prezentują strukturę statystyczną prognoz uzyskiwanych dla 10 sieci zbudowanych przy identycznych
parametrach. Zaznaczone są ( licząc od dołu ) minimum, kwartyl pierwszy, mediana, kwartyl trzeci i
maksimum uzyskanych błędów. Słupek niski oznacza, że w 10 próbach uzyskiwano podobne
prognozy. Słupek wysoki oznacza, że wyniki te różniły się znacznie. Ponieważ wiele z nich wskazuje
na istotną asymetrię prognoz dodatkowo linią czerwoną oznaczono mediany prognoz. Minimalny błąd
równy 0.81% uzyskano dla 26 opóźnień. Wynik jest istotnie lepszy niż założone minimum 1.28%.
Należy tu zauważyć, że prognozy dla 26 opóźnień są bardzo zróżnicowane ( wysoki słupek ) a
mediana jest „nisko”. Oznacza to, że zdarzały się nieliczne prognozy znacznie gorsze.
Sieci z jedną warstwą ukrytą są dość szybkie, jednak mogą być stosunkowo mało czułe. Aby
zwiększyć czułość sieci, czyli jej zdolność do uchwycenia delikatnych zmian, można zwiększyć liczbę
warstw ukrytych. Niekorzystną konsekwencją takiego zabiegu jest gwałtowne zwiększenie czasu
uczenia sieci i jej wymagania co do ilości pamięci w komputerze. Sieć może się zacząć uczyć „szumu”
a więc losowych i nieistotnych zmian w danych uczących. Sprawdźmy więc czy dodanie drugiej
warstwy ukrytej nie pozwoli zbudować lepszych prognoz. Wszystkie parametry uczenia sieci
pozostają bez zmian. Dodajemy drugą warstwę ukrytą z liczbą neuronów równa liczbie w pierwszej
warstwie ukrytej.
Rys. 5 Nowa sieć.
8
MAPE (Mean Absolute Prediction Error). Średni, absolutny ( tu procentowy) błąd prognozy.
Rys.6 ( 142 minuty pracy komputara )
Jak widzimy na wykresie 6 nie udało się uzyskać istotnego polepszenia prognoz. Minimalny błąd
0.79% uzyskano dla 37 opóźnień. Również i tym razem rozproszenie prognoz jest tu spore. Czas
analizy zwiększył się jednak trzykrotnie.
PROGNOZY WIG’U NA PODSTAWIE WSKAŹNIKÓW TECHNICZNYCH
Nawet podstawowe badania byłyby niepełne gdybyśmy nie spróbowali przetestować użyteczności
danych technicznych w prognozowaniu wartości WIG. Podstawową trudnością jest dobór wskaźników
i ich parametrów. Uznaliśmy, że w prezentowanych badaniach zastosujemy jedynie najpopularniejsze
wskaźniki z klasycznymi parametrami podawanymi przez Murphy’ege w jego „Analizie
Technicznej”9. Zbiór wskaźników jest następujący :
1. wstęga Bollingera ( 9, 2, -2 )
2. CCI ( 20, 10, 100, -100 )
3. MACD ( 12, 26, 9 )
4. momentum ( 10 )
5. średnie kroczące ( 4, 8, 9, 12, 18, 24 ) okresowe
6. Ważone średnia krocząca ( 9 )
7. przesunięta średnia krocząca ( 9, 5 )
8. wykładnicza średnia krocząca ( 9 )
9. OBV
10. ROC ( 10 )
11. RSI ( 14, 20 , 80 )
12. Ultimate Osc. ( 7, 14, 28 )
13. Volume Osc. ( 14, 34 )
Z szeregów wyeliminowano stałe ( np. wartości progów RSI 20 i 80, które stanowią dwa szeregi o
powtarzających się wartościach odpowiednio 20 i 80 ). W ten sposób pozostało 20 zmiennych
objaśniających. Dodatkowo wprowadzono opóźnienia o 2 i 3 okresy wszystkich szeregów. W sumie
poddano analizie 60 zmiennych. Analizie poddano sesje od 400 do 1650. Zbiór danych podzielono na
3 części. Sesje 402, 406, 410, 414 ... potraktowano jako zbiór testowy ( 25% obserwacji ). Sesje 404,
408, 412, 416 ... potraktowano jako zbiór próbek korygujących uczenie sieci ( 25% obserwacji ).
Pozostałe sesje posłużyły jako zbiór uczący ( 50% obserwacji ). Zbudowano sieć o jednej warstwie
ukrytej gdzie na wejściu było 60 neuronów wejściowych. Liczbę neuronów warstwy ukrytej
optymalizowano w przedziale (1, 50). Sieć o bieżącej liczbie neuronów uczono dziesięciokrotnie. Na
wyjściu jest jeden neuron. Wszystkie dane przeskalowano na przedział (0, 1). Jako funkcje aktywacji
zastosowano funkcję logistyczną. Krok uczenia ustalono na 0.02. Proces uczenia był przerywany jeżeli
:
1. przekroczony został limit 50 epok ( nie zdarzyło się to ani razu )
2. przekroczony został czas 10 minut uczenia sieci ( nie zdarzyło się to ani razu )
3. został osiągnięty maksymalny dopuszczalny błąd sieci ustalony na poziomie 0.0001.
4. po kolejnych 5 epokach mimo dalszego uczenia sieci nie uzyskiwano poprawy generalizacji
sieci ( jakości prognoz ).
Przy tak dużej sieci gwałtownie wzrosły wymagania co do mocy i pamięci komputera. Pełna analiza
zajęła 51 minut. Jednak maksymalny czas jaki mogła ona zająć wynosił 50*10*10/60 = 83.33
godziny10. Należy pamiętać, że tak krótki czas uczenia pojedynczej sieci można ustalić na komputerze
wyposażonym w ogromną ilość pamięci. Przy zastosowaniu 64MB, gdy większość operacji jest
buforowanych na dysku czas ten należy wydłużyć przynajmniej czterokrotnie. W przeciwnym
wypadku SN nie będzie maiła szans na nauczenie się czegokolwiek. Wyniki uzyskane przez najlepszą
uzyskaną sieć są jednak gorsze niż poprzednio ( rys.7 ). Zwiększanie liczby neuronów nie dawało
żadnej systematycznej poprawy. Sieć o 27 neuronach uzyskała błąd na poziomie 1.4%. Jak widać był
to raczej „dobry traf”. Średnia z 10 prób jest tu jedną z najgorszych ze wszystkich uzyskanych. Mimo
to zgodność przebiegów WIG’u i jego prognoz była bardzo dobra. Na rysunku 8 widzimy WIG i
uzyskane tu prognozy. Prognozowana jest co czwarta sesja od 401 począwszy.
9
J.J.Murphy, „Analiza Techniczna”, WIG-PRES, Wa-wa 1995.
Opóźnienia od 1 do 50, każde testowane 10 razy, każdy test maksimum 10 minut.
10
RYS.7
RYS.8
( Wartość na osi X równa 50 oznacza sesję o numerze 401+50*4 = 601)
Widzimy tu typowy fragment prognoz. Wiele z nich jest niemal idealnych ( punkty 27,
34,40,47,49,50). Jednak znajdują się także serie prognoz zupełnie nie udanych ( 28-35 ).
Rys. 9
Na rysunku 9 widzimy rozkład procentowych błędów prognoz dla najlepszej uzyskanej w
optymalizacji sieci. Widać, że zdecydowana większość błędów zawiera się w przedziale ( –1.5 , 1.5 )
procenta. Jest poniżej 10% błędów przewyższających ± 3%. Linia czerwona pokazuje jak powinny
kształtować się liczebności błędów gdyby miały one rozkład Gaussa. Wyniki próby poprawienia
wyników przez dodanie drugiej warstwy ukrytej przedstawione są na rysunku 10. W drugiej warstwie
ukrytej zastosowano tą samą liczbę neuronów co w warstwie pierwszej.
RYS.10 ( 1772 minuty pracy komputera )
Jak widzimy nie udało się uzyskać żadnej poprawy. Minimalny błąd wyniósł 1.43% przy 9 neuronach.
Gwałtowny wzrost błędów powyżej 36 neuronów jest spowodowany brakiem pamięci komputera.
Gdy sieć zajęła całą dostępną pamięć czas uczenia pojedynczej epoki wzrasta wielokrotnie. Z
łatwością przekracza całkowity czas uczenia sieci. W związku z tym sieć nie uczy się „prawie nic” i
takie też generuje prognozy. Dane te nie mogą być interpretowane. Podsumowując możemy
powiedzieć, że sieć oparta na wskaźnikach technicznych11 nie dała znaczącej poprawy w
prognozowaniu WIG’u w stosunku do sieci uwzględniającej jedynie własne opóźnienia WIG.
11
W tym ujęciu. Można oczywiście użyć innych wskaźników. Można także użyć tych samych ale ze zoptymalizowanymi
parametrami. Można zwiększyć liczbę opóźnień uwzględnionych w analizie. Nie jest to w żadnym razie dyskwalifikacja
AT.
SYSTEM INWESTYCYJNY
Zestawy prognoz krótko i średnio terminowych prezentowane powyżej pozwalają zbudować wiele
mechanicznych systemów inwestycyjnych. Najprostszym rozwiązaniem byłoby potraktowanie tych
prognoz jako oscylatorów. Prognozy krótkoterminowe jako oscylator wolny a średnioterminowe jako
szybki. Ta nie intuicyjna kolejność spowodowana jest tym ,że przeciwnie niż przy innych wskaźnikach
oba te oscylatory są równie wrażliwe. Prognoza na 5 sesji naprzód będzie zawsze „szybsza” niż na
jedną sesję. Tak więc, jeżeli linia prognoz średnioterminowych przetnie z dołu krótkoterminową o
zadaną liczbę punktów będzie to sygnał kupna. Jeżeli przecięcie nastąpi z góry będzie to sygnał
sprzedaży. Aby wykluczyć przypadkowe słabe sygnały należy ustalić wartość progową kiedy sygnał
uważamy za ważny. Wysokość progu jest sprawą indywidualną i będzie ustalana arbitralnie. Dla
przykładu inwestując w WIG na przestrzeni roku począwszy od sesji 1301 ustalając wartości prognoz
optymalnymi sieciami uzyskanymi w powyższej analizie, przyjmując wartość progową mocy sygnału
na 150 punktów uzyskano następujące sygnały :
Tab.1
PROCENT
NR
ZYSKU
TRANSAKCJI NR SESJI NR SESJI PROCENT
KUPNA SPRZEDARZY ZYSKU SKUMULOWANY
1
1323
1336
-2.22
-2.22
2
1342
1345
0.94
-1.28
3
1349
1357
3.19
1.91
4
-14.05
1358
1375
-12.14
5
1377
1380
1.63
-10.51
6
1389
1391
1.22
-9.30
7
1400
1401
-0.09
-9.38
8
1410
1411
-2.89
-12.27
9
1413
1416
1.54
-10.73
10
1418
1421
2.61
-8.13
11
1428
1458
4.11
-4.02
12
1461
1463
-3.96
-7.98
13
18.45
1470
1480
10.48
14
1481
1487
-1.87
8.61
15
1494
1508
-3.35
5.26
16
1509
1511
-0.06
5.20
17
1513
1521
3.75
8.96
18
1525
1541
5.36
14.31
19
11.50
1542
1586
25.82
20
1587
1600
4.94
30.75
21
1617
1625
-1.44
29.32
22
1627
1630
2.45
31.77
23
32.57
1636
1645
0.80
W analizowanym okresie przy powyższych założeniach uzyskaliśmy 23 sygnały. Można było uzyskać
32.57% zysku. Zdecydowana większość transakcji dawała małe zyski a czasem straty. Trzy transakcje
były wysokie w tym dwie „udane”. Wyliczenia powyższe nie uwzględniają prowizji maklerskich.
Kilka „małych udanych” transakcji w rzeczywistości byłoby „nieudanych”. Rzeczywista efektywność
brutto byłaby oczywiście nieco niższa niż 30%. Ocena tego wyniku to już indywidualna sprawa
każdego inwestora. Niewątpliwie jest to znacznie lepszy wynik niż obligacje państwowe czy lokaty
bankowe. Z pewnością da się jednak znaleźć efektywniejsze strategie.
WNIOSKI
Przedstawiliśmy wyniki prostych badań nad zdolnościami sieci neuronowych w prognozowaniu
indeksu WIG. Dostarczają one dość obiecujących informacji. Udało się zbudować prognozy kierunku
zmian WIG’u o ponad 80% skuteczności w krótkim i średnim horyzoncie. Prognozy wartości indeksu
również są zadowalające. Oczywiście należy sobie zdawać sprawę, że pokazane tu ujęcie jest tylko
jednym z bardzo wielu możliwych. Wyniki te nie są ostateczne a mają jedynie zachęcić do
samodzielnych badań. Istnieje wiele innych typów sieci, które należało by przetestować. Powinno się
optymalizować również inne parametry sieci niż tylko liczbę neuronów w warstwach ukrytych.
Należało by zoptymalizować wartości współczynników technicznych analizowanych w ostatnim
przykładzie, sprawdzić wpływ informacji fundamentalnych na możliwości prognostyczne. Można by
zbudować sieć „rozpoznającą” formacje techniczne – do wspomagania prognoz długoterminowych.
Dróg poprawy prezentowanych wyników jest wiele…
Więcej informacji technicznych i merytorycznych dotyczących powyższego artykułu można znaleźć na stronie internetowej:
http://www.bg.univ.gda.pl/~Najman/sn/sn.htm Zamieszczamy tam także podstawowe informacje o programowaniu w
MATLAB’ie a także kody źródłowe większości analiz prezentowanych w artykule.