Sieci neuronowe

Sieci neuronowe
Sztuczne sieci neuronowe (SSN) powstały jako system symulujący pracę mózgu.
Podstawową jednostką budowy biologicznego układu nerwowego jest neuron. Ilość neuronów
w mózgu jest rzędu 1018. Neurony te są połączone ze sobą, tworząc skomplikowaną strukturę,
przez którą przechodzą z dużą częstotliwością impulsy elektryczne. Pojedyncza komórka
nerwowa składa się z jądra, wielu dendrytów (których celem jest pobieranie impulsów
z innych neuronów) i jednego aksonu, który przekazuje impuls dalej. Sztuczne neurony nie są
dokładnymi kopiami oryginalnych neuronów, są raczej ich logicznymi odpowiednikami,
mającymi podobne właściwości i działającymi tak jak ich pierwowzory.
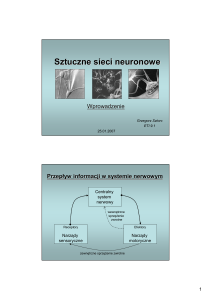
rys 1. Schemat budowy sztucznego neuronu.
Sposób działania pojedynczego neuronu jest następujący:
Do wejść doprowadzane są sygnały (xi) dochodzące z neuronów warstwy poprzedniej. Każdy
sygnał mnożony jest przez odpowiadającą mu wartość liczbową (zwaną wagą wi) a następnie
są one sumowane (co odpowiada matematycznej operacji iloczynu skalarnego wektora
sygnału wejściowego i wektora wag).
n
s = ∑ wi xi
i =1
Powstała w wyniku sumowania wartość s stanowi argument funkcji aktywacji neuronu f(s).
W ten sposób otrzymujemy sygnał wyjściowy neuronu y = f(s).
Żeby neurony wykonywały określone zadania trzeba je połączyć w zorganizowaną
strukturę. Najczęściej stosuje się sieci warstwowe (perceptrony), czyli takie gdzie neurony
podzielone są na warstwy, a każdy neuron w warstwie jest połączony ze wszystkimi
neuronami z warstwy poprzedniej. Pierwszą warstwę nazywamy warstwą wejściową, ostatnią
wyjściową, a wszystkie pomiędzy nimi to warstwy ukryte. Do różnych zadań wykorzystuje
się sieci o różnej liczbie warstw, z tym że nie tworzy się sieci o liczbie warstw ukrytych
większej niż trzy. Nie zauważono bowiem aby ich skuteczność była większa niż w sieciach
o trzech warstwach ukrytych, natomiast wzrasta komplikacja sieci, co powoduje spowolnienie
jej działania. Zasadne jest za to zwiększanie ilości komórek w warstwie, co może
spowodować zwiększenie efektywności sieci.
rys 2. Model trójwarstwowej sieci neuronowej.
Oprócz sieci warstwowych jednokierunkowych tworzy się też sieci rekurencyjne.
W sieciach tego typu występuje tzw. sprzężenie zwrotne między warstwą wyjściową
a warstwą wejściową. Oznacza to, że sygnały na wyjściu podawane są na wejścia warstwy
wejściowej. Sygnały wejściowe w takiej sieci zależą zarówno od aktualnego stanu wejścia jak
i od sygnałów wyjściowych w poprzednim cyklu.
Jak łatwo zauważyć reakcja sieci zależy od ustawień poszczególnych wag. Dlatego
proces nauczania polega na odpowiednim ich ustawieniu. Najbardziej rozpowszechnionym
i zarazem najbardziej intuicyjnym sposobem nauczania jest tzw. uczenie z nauczycielem.
Polega ono na tym że sieci (o losowym ustawieniu wag) daje się do rozwiązania jakieś
zadanie, którego rozwiązanie jest nam znane. Odpowiedź sieci będzie oczywiście błędna,
więc modyfikujemy w odpowiedni sposób (propagacja wsteczna błędu) niektóre, lub
wszystkie wagi. Dajemy następne zadanie i znowu modyfikujemy wagi w zależności od
poprawności odpowiedzi. Kontynuujemy to tak długo, aż sieć będzie poprawnie reagowała na
wszystkie (lub zadowalającą większość) zadań.
Po treningu przeprowadza się testy, podczas których sieć nie zna prawidłowych
rozwiązań a podane przez nią rozwiązanie jest porównywane z prawidłowym.
Ważniejsze kierunki zastosowań to:
•
Predykcja
Sieci neuronowe są często wykorzystywane, aby na podstawie pewnych danych
wejściowych przewidywać dane wejściowe. Ważną zaletą jest to, że sieć może nauczyć
się przewidywania sygnałów wyjściowych bez jawnego definiowania związku między
danymi wejściowymi a wyjściowymi.
•
Klasyfikacja i rozpoznawanie
Zadanie polega na przewidywaniu identyfikatora klasy, do której dany obiekt należy.
Przykładem może być tu sieć pozwalająca na podstawie danych bilansowych stwierdzić,
czy dane przedsiębiorstwo należy do zwyżkujących gospodarczo, przeżywa stagnację czy
też grozi mu regres.
•
Kojarzenie danych
Klasyczne systemy komputerowe mogą gromadzić duże zbiory danych bez możliwości
ich kojarzenia. Sieci neuronowe, dzięki zdolności uczenia się i uogólniania doświadczeń,
pozwalają zautomatyzować procesy wnioskowania i pomagają wykrywać istotne
powiązania pomiędzy danymi.
•
Analiza danych
Zadanie polega na znalezieniu związków pomiędzy danymi. Realizacja tego zadania przez
sieci neuronowe daje nowe możliwości w zakresie prowadzenia analiz ekonomicznych.
•
Filtracja sygnałów
Dane gospodarcze pochodzące z różnych źródeł są zakłócone. Klasyczne metody
eliminacji "szumów" pozwalają usunąć zakłócenia o charakterze losowym, lecz nie dają
podstaw do eliminacji przekłamań systematycznych. Coraz częściej zatem bada się
możliwość zastosowania sieci neuronowych jako filtrów danych.
•
Optymalizacja
Doświadczalnie potwierdzono możliwości sieci do rozwiązywania zadań optymalizacji
statycznej i dynamicznej. Szczególnie ciekawe jest zastosowanie sieci do optymalizacji
kombinatorycznej i zagadnień bardzo trudnych obliczeniowo (również np-zupełnych),
które mogą być rozwiązane w krótkim czasie dzięki współbieżnemu wyliczaniu przez
wiele elementów sieci.
Literatura:
[1] Stanisław Osowski: Sieci neuronowe w ujęciu algorytmicznym, WNT, Warszawa 1997,
[2] Ryszard Tadeusiewicz: Sieci neuronowe, AOW, Warszawa 1993.