Kryptografia - zastosowanie krzywych eliptycznych

Kryptografia - zastosowanie krzywych
eliptycznych
Mariusz Frydrych
24 marca 2011
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Niech F bedzie
˛
ciałem doskonałym (tzn. każde rozszerzenie
algebraiczne ciała F jest rozdzielcze lub równoważnie,
monomorfizm Frobeniusa jest izomorfizmem), np. ciała
charakterystyki zero lub ciała skończone.
Definicja
Krzywa˛ eliptyczna˛ E(F) nad ciałem F nazywamy dowolna˛
rzutowa,
˛ gładka˛ krzywa˛ algebraiczna˛ genusu jeden nad ciałem
F z wyróżnionym punktem bazowym O.
Niech D ∈ Div(C) bedzie dowolnym dywizorem gładkiej krzywej
rzutowej C nad ciałem F. Określmy zbiór
L(D) = {f ∈ F(C) : div (f ) + D ≥ 0} ∪ {0},
bed
˛ acy
˛ skończenie wymiarowa˛ przestrzenia˛ wektorowa˛ nad
ciałem F wymiaru `(D), tzn.
`(D) = dimF L(D).
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Definicja
Dla dowolnego (nie zależy od wyboru) dywizora kanonicznego
KC krzywej C liczbe˛ całkowita˛ nieujemna˛ `(KC ) nazywamy
genusem krzywej C i oznaczamy przez g, tzn.
g = `(KC )
Uwaga
W przypadku ciała liczb zespolonych (F = C) krzywa˛ X
nazywamy powierzchnia˛ Riemanna a jej genus g jest równy
wymiarowi pierwszej grupy kohomologii powierzchni X o
współczynnikach w snopie funkcji holomorficznych, tzn.
g = dimC H1 (X , O)
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Twierdzenie (Riemanna-Rocha)
Niech C bedzie
˛
dowolna˛ gładka,
˛ rzutowa˛ krzywa˛ algebraiczna˛
nad ciałem F. Wtedy dla każdego dywizora D ∈ Div(C)
zachodzi równość
`(D) − `(KC − D) = 1 − g + deg D.
Mariusz Frydrych
(1)
Kryptografia - zastosowanie krzywych eliptycznych
Wniosek
`(KC ) = g, definicja genusu
deg KC = 2g − 2 = −χ(C), minus charakterystyka Eulera
krzywej C
Jeśli deg D > 2g − 2, to
`(D) = 1 − g + deg D.
(2)
deg D > 0 =⇒ `(D) = deg D.
(3)
Jesli g=1, to
Korzystajac
˛ z twierdzenia Riemanna-Rocha (1) można
pokazać, że każda˛ krzywa˛ eliptyczna˛ można sprowadzić do
płaskiej rzutowej krzywej w tzw. postaci Weierstrassa
C ⊂ P2 (F).
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Postać Weierstrassa krzywej eliptycznej
Rozważmy równanie dwóch zmiennych X , Y w ciele F
(dowolnej charakterystyki)
Y 2 + a1 XY + a3 Y = X 3 + a2 X 2 + a4 X + a6
(4)
gdzie a1 , a2 , a3 , a4 , a6 ∈ F.
Jeżeli ciało K jest rozszerzeniem ciała F (F ⊂ K), to przez E(K)
oznaczamy zbiór punktów K-wymiernych krzywej, tzn. zbiór
par (x, y ) ∈ K2 spełniajacych
˛
równanie (4).
Mówimy, że krzywa (4) jest gładka, gdy w każdym punkcie
F-wymiernym, gdzie F jest domknieciem
˛
algebraicznym ciała F,
nie zachodza˛ równocześnie równania
a1 Y = 3X 2 + 2a2 X + a4
2Y + a1 X + a3 = 0
(5)
∂
∂
otrzymane z (4) przez różniczki czastkowe
˛
∂X i ∂Y .
Krzywa˛ gładka˛ zadana˛ równaniem (4) nazywamy krzywa˛
eliptyczna˛ w postaci Weierstrassa.
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Uwaga
W przypadku ciała charakterysyki różnej od 2 (χ(F) 6= 2)
podstawienie
y 7−→
1
(y − a1 x − a3 )
2
(6)
prowadzi równanie krzywej do postaci
y 2 = 4x 3 + b2 x 2 + 2b4 x + b6
(7)
gdzie
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Uwaga
b2 = a12 + 4a4 , b4 = 2a4 + a1 a3 , b6 = a32 + 4a6
(8)
a12 a6 + 4a2 a6 − a1 a3 a4 + a2 a32 −
b22 − 24b4
−b23 + 36b2 b4 − 216b6
−b22 b8 − 8b43 − 27b62 + 9b2 b4 b6
c43
(9)
b8 =
c4 =
c6 =
∆ =
j =
ω =
a42
∆
dx
dy
=
2
2y + a1 x + a3
3x + 2a2 x + a4 − a1 y
(10)
(11)
(12)
(13)
(14)
Powyższe wielkości spełniaja˛ zależności:
4b8 = b2 b6 − b42
1728∆ =
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
−
c62
(15)
c43
(16)
W zależności od charakterystyki ciała F równanie (4) krzywej
eliptycznej można sprowadzić do prostszej postaci:
w przypadku χ(F) = 2 wyróżniamy dwa typy krzywych:
supersingularny
Y 2 + a3 Y = X 3 + a4 X + a6
niesupersingularny:
Y 2 + XY = X 3 + a2 X 2 + a6
jeżeli χ(F) 6= 2 to
Y 2 = X 3 + a2 X 2 + a4 X + a6
jeżeli χ(F) 6= 2, 3 to
Y 2 = X 3 + a4 X + a6
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
W charakterystyce różnej od 2 i 3 równanie (4) możemy
zapisać w postaci:
Y 2 = X 3 + aX + b
(17)
a warunki gładkości (5) sa˛ równoważne temu by wielomian po
prawej stronie nie miał pierwiastków wielokrotnych, co z kolei
jest równoważne nieznikaniu wyróżnika ∆ 6= 0. Wyróżnik
wielomianu unormowanego stopnia n o pierwiastkach
c1 , c2 , . . . cn jest równy
Y
Y
∆=
(cj − ck ) = (−1)n(n−1)/2 (cj − ck )2
j6=k
j<k
co w przypadku wielomianu X 3 + aX + b oznacza
∆ = −(4a3 + 27b2 ).
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
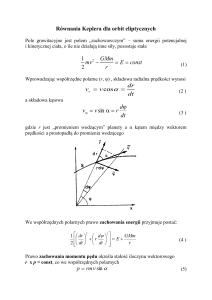
Krzywe eliptyczne na ciałem liczb rzeczywistych R
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Reguły dodawania punktów na krzywej eliptycznej nad ciałem R
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Jeśli M1 (x1 , y1 ), M2 (x2 , y2 ), M3 (x3 , y3 ), P(x3 , −y3 ) to
współrz˛edne punktu M3 = M1 + M2 wyrażaja˛ sie˛ wzorami:
jeśli M1 6= M2 to
y2 − y1 2
− x1 − x2
x3 =
x − x1
2
y2 − y1
y3 = −y1 +
(x1 − x3 )
x2 − x1
dla x1 6= x2 i O "punkt w nieskończoności" w przeciwnym
przypadku
jeśli M1 = M2 to
!
3x12 + a
x3 =
− 2x1
2y1
!
3x12 + a
(x1 − x3 )
y3 = −y1 +
2y1
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
W przypadku ciała liczb zespolonych C krzywa eliptyczna dana
równaniem (17) jest powierzchnia˛ Riemanna (jednowymiarowa˛
rozmaitościa˛ zespolona)
˛ genusu g = 1 czyli torusem.
Rozważmy całk˛e eliptyczna˛
Z
dX
√
3
X + aX + b
γ
(18)
liczby zespolone ω1 , ω2 ∈ C (całki po krzywych zamknietych
˛
generujace
˛ pierwsza˛ grupe˛ homologii torusa H1 (E(C), Z))
wyznaczaja˛ krate˛ Λ w C.
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Powyższa krata Λ definiuje funkcje˛ Weierstrassa
X 1
1
1
℘(z, Λ) = 2 +
−
z
(z − ω)2 ω 2
(19)
ω∈Λ\{0}
Funkcja Weirestrassa jest 2-okresowa, tzn.
℘(z, Λ) = ℘(z + ω, Λ) i wraz ze swoja˛ pochodna˛ (zespolona)
˛
spełnia równanie
℘0 (z, Λ)2 = 4℘(z, Λ)3 − g2 ℘(z, Λ) − g3
(20)
gdzie g2 = 60G4 (Λ), g3 = 140G6 (Λ) a
G2k =
X
ω∈Λ\{0}
1
ω 2k
(21)
sa˛ niezmienikami Eiesensteina kraty Λ.
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
W przypadku ciała skończonego Galois Fpn (p jest liczba˛
pierwsza˛ a n naturalna,
˛ oznaczmy q = pn ) rozważmy szereg
formalny zmiennej T
ζ(E(Fq ), T ) = exp
∞
X
Nr T r /r
(22)
r =1
gdzie liczby Nr oznaczaja˛ liczbe˛ punktów Fq r wymiernych
kolejnych rozszerzeń ciała Fq . Szereg (22) jest szczególnym
przypadkiem słynnej funkcji zeta Riemanna.
Mariusz Frydrych
Kryptografia - zastosowanie krzywych eliptycznych
Twierdzenie (Hipoteza Weila dla krzywych eliptycznych twierdzenie Hassego-Deligne)
Powyższy szereg formalny (22) jest prosta˛ funkcja˛ wymierna˛
(tzn. ζ(E(Fq ), T ) ∈ Q[T ])
ζ(E(Fq ), T ) =
1 − aT + qT 2
(1 − T )(1 − qT )
(23)
Ponadto
1 − aT + qT 2 = (1 − αT )(1 − βT ), |α| = |β| =
√
q
(24)
gdzie a ∈ Z spełnia zależność
a = q + 1 − N1
Mariusz Frydrych
(25)
Kryptografia - zastosowanie krzywych eliptycznych
Wniosek
Z (24 i 25) otrzymujemy oszacowanie na ilość N = N1 punktów
Fq wymiernych krzywej eliptycznej zdefinowanej nad ciałem Fq
√
√
q + 1 − 2 q ≤ N ≤ q + 1 + 2 q.
(26)
Liczby Nr odzyskujemy z funkcji zeta Riemanna (22) za
pomoca˛ formuły:
Nr =
1
dn
log ζ(E(Fq ), T )|T =0
(n − 1)! dT n
Mariusz Frydrych
(27)
Kryptografia - zastosowanie krzywych eliptycznych