ZADANIA 14-15_II_e_zad_roz

EUROELEKTRA
Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej
Rok szkolny 2014/2015
Zadania z elektrotechniki na zawody II stopnia
(grupa elektryczna)
Zadanie 1
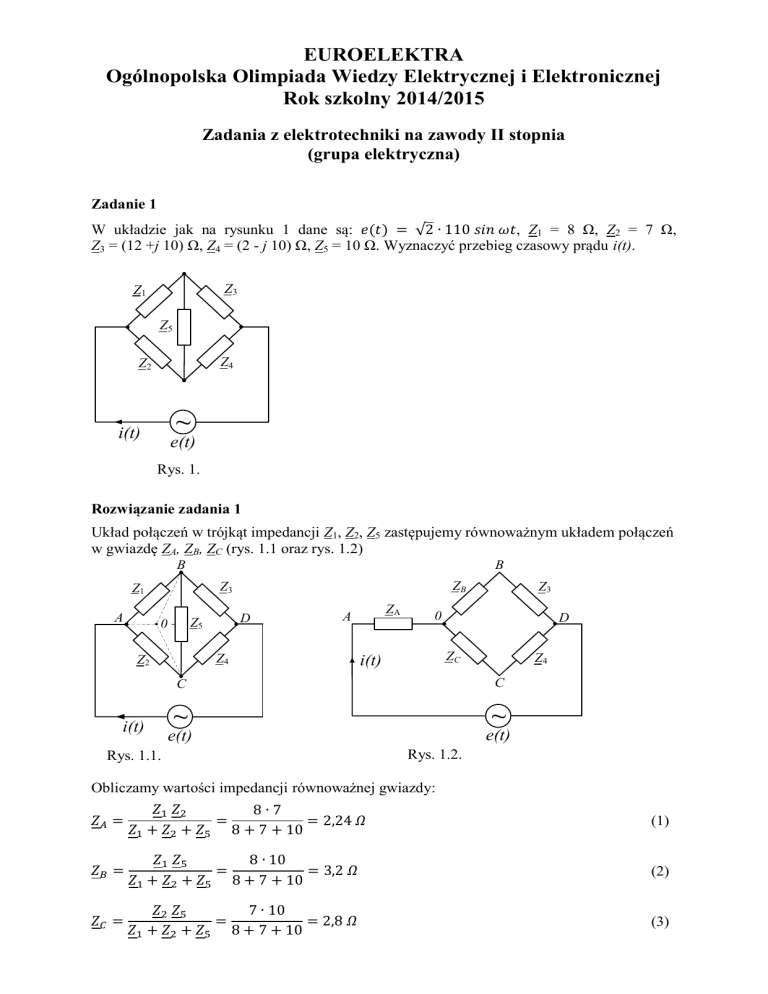
W układzie jak na rysunku 1 dane są:
, Z1 = 8 Ω, Z2 = 7 Ω,
Z3 = (12 +j 10) Ω, Z4 = (2 - j 10) Ω, Z5 = 10 Ω. Wyznaczyć przebieg czasowy prądu i(t).
Z3
Z1
Z5
Z4
Z2
~
i(t)
e(t)
Rys. 1.
Rozwiązanie zadania 1
Układ połączeń w trójkąt impedancji Z1, Z2, Z5 zastępujemy równoważnym układem połączeń
w gwiazdę ZA, ZB, ZC (rys. 1.1 oraz rys. 1.2)
B
B
A
ZB
Z3
Z1
D
Z5
0
Z4
Z2
ZA
A
0
D
ZC
i(t)
Rys. 1.1.
Z4
C
C
i(t)
Z3
~
~
e(t)
e(t)
Rys. 1.2.
Obliczamy wartości impedancji równoważnej gwiazdy:
(1)
(2)
(3)
Impedancja między punktami 0-D wynosi
(4)
Impedancja zastępcza obwodu (rys. 1.2) wynosi:
(5)
Maksymalny prąd pobierany z sieci obliczamy z zależności:
(6)
Kąt przesunięcia między wektorami prądu I oraz napięcia E wynosi:
(7)
Obwód ma charakter R-C, więc prąd wyprzedza napięcie o kąt 26°. Przebieg prądu
przedstawia funkcja:
(8)
Zadanie 2
Do symetrycznej sieci trójfazowej skojarzonej w gwiazdę o napięciach:
uA t   2  230  sin  t  V,
2π 

uB t   2  230  sin   t 
 V,
3 

4π 

uC t   2  230  sin   t 
 V,
3 

przyłączono odbiornik trójfazowy symetryczny połączony w gwiazdę (rys. 2) o impedancji
ZA = ZB = ZC = Z = (60 + j80) Ω. Obliczyć wskazania watomierza W włączonego w obwód
jak na rysunku 2. Ile wynosi moc czynna i bierna całego układu ?
uA(t)
uC(t)
Z
uB(t)
Z
Z
W
Rys. 2.
Rozwiązanie zadania 2
Cewka prądowa watomierza jest włączona w fazie „B” – przez watomierz płynie prąd fazowy
IB. Wartość skuteczna tego prądu wynosi:
(1)
Cewka napięciowa watomierza jest przyłączona na napięcie międzyfazowe UAC, którego
wartość skuteczna wynosi
(2)
Kąt przesunięcia pomiędzy napięciem a prądem odbiornika w jednej fazie wynosi (z trójkąta
impedancji):
(3)
Wyznaczamy kąt α pomiędzy wektorem napięcia UAC i wektorem prądu IB, na podstawie
wykresu wskazowego (rys.2.1):
UA
UAC
UAC
90
UC
IB
φodb
UB
Rys. 2.1.
(4)
Wskazanie watomierza W wynosi:
(5)
Znak „-” oznacza, że aby watomierz wychylił się „w prawo” należy zamienić początek i
koniec cewki prądowej.
Układ trójfazowy jest symetryczny. Moc czynna układu wynosi:
(6)
natomiast moc bierna:
(7)
Zadanie 3
Transformator jednofazowy ma następujące dane znamionowe: SN = 5,0 kVA, U1N = 400 V,
U2N = 110 V, napięcie zwarcia uz = 4,5%, straty w uzwojeniach ΔPCu = 150 W przy
obciążeniu prądem znamionowym, prąd stanu jałowego I0 = 9,0%, straty mocy w stanie
jałowym ΔP0 = 60 W. Rezystancja uzwojenia strony pierwotnej transformatora wynosi
RCu1 = 0,48 Ω, natomiast strony wtórnej RCu2 = 0,036 Ω. Obie rezystancje wyznaczone są przy
temperaturze 75 ºC. W trakcie remontu transformatora, zmniejszono przekrój przewodu
nawojowego po stronie pierwotnej o 20%, a po stronie wtórnej o 10%. Należy obliczyć prąd,
który płynie w uzwojeniach transformatora po remoncie, jeżeli wiadomo, że wartość strat w
uzwojeniach równa jest znamionowym stratom mocy w uzwojeniach przed przezwojeniem
transformatora. Należy przyjąć, że długość przewodu i liczba zwojów nie ulega zmianie, a
temperatura uzwojeń jest równa 75 ºC, czyli temperaturze uzwojeń, przy której wyznaczono
znamionowe straty mocy w uzwojeniach.
Rozwiązanie zadania 3
Zmniejszenie przekroju przewodu nawojowego powoduje, że rezystancja uzwojeń zwiększy
się:
- obliczamy rezystancję uzwojenia strony pierwotnej transformatora:
(1)
- obliczamy rezystancję uzwojenia strony wtórnej transformatora:
(2)
Prąd znamionowy transformatora wynosi:
(3)
Straty w uzwojeniach transformatora obliczamy z zależności:
(4)
Ponieważ:
(5)
to prąd strony pierwotnej będzie równy:
(6)
Prąd strony wtórnej:
(7)
Zadanie 4
Świetlówkę o poborze mocy 40 W włączono w szereg z dławikiem ograniczającym na
napięcie 220 V (50 Hz) (rys. 3) i stwierdzono, że prąd pobierany z sieci wynosi 0,38 A. Moc
tracona w dławiku wynosi 9,0 W. Należy obliczyć współczynnik mocy świetlówki
z dławikiem, indukcyjność dławika, pojemność kondensatora potrzebnego do poprawienia
współczynnika mocy do wartości cosφw = 0,950 (tgφw = 0,329) oraz prąd pobierany z sieci po
kompensacji i prąd płynący przez kondensator. Dla uproszczenia można założyć, że
świetlówka zachowuje się jak rezystor.
a)
b)
I
świetlówka
Iw
A
I świetlówka
A
Ik
U
V
U
L, Rdł
V
C
L, Rdł
Rys. 3. Układ połączeń świetlówki a) bez poprawiania współczynnika mocy,
b) z kondensatorem do poprawienia współczynnika mocy
Rozwiązanie zadania 4
Współczynnik mocy przed kompensacją:
cos  
P
40  9

 0,583
UI 220  0,38
(1)

 P 
tg  tg  arccos     tg arccos 0,583  1,385
 UI  

(2)
Pojemność kondensatora:
C
Qk
U
2

Ptg  tgw 
2fU
2

49  1,385  0,328
2  50    220
2
 3,4  106 F  3,4 F
(3)
Przyjmując, że świetlówka zachowuje się jak rezystor, obliczamy napięcie na świetlówce:
U sw 
P
40

 105 V
I 0,38
(4)
Napicie na rezystancji dławika:
P
9
U R  dł 
 24 V
I
0,38
(5)
Napięcie na indukcyjności dławika
U L  U 2  U sw  U R 2  2202  1292  178 V
Napięcie na dławiku:
(6)
U L  1782  242  180 V
(7)
Indukcyjność dławika:
U
178
L L 
 1,49 H
2fI 2  50  0,38
Prąd pobierany z sieci po kompensacji:
(8)
Iw 
P
49

 0,234 A
U cos w 220  0,95
(9)
Prąd płynący przez kondensator
I k  2fCU  2  50  3,4 106  220  0,235 A
(10)
Zadanie 5
Moc żarówki 100 W/110 V jest zmieniana za pomocą regulacji kąta zapłonu tyrystora
zasilanego z prostownika jednopołówkowego sterowanego napięciem zmiennym U = En
o wartości skutecznej 110 V (za pośrednictwem autotransformatora 220 V/110 V).
a) Jakie wartości skuteczne napięcia i prądu występują w obwodzie w przypadku kąta zapłonu
θF = 0°. Wartość stosunku napięcia skutecznego do napięcia maksymalnego przy kącie
θF = 0° przyjąć równą 0,5.
b) Jakie są wartości średnie napięcia na żarówce zmierzonego woltomierzem prądu stałego
i prądu płynącego przez żarówkę zmierzonego amperomierzem prądu stałego w przypadku
kąta θF = 0°. Wartość stosunku napięcia średniego do napięcia maksymalnego przy kącie
θF = 0° przyjąć równą 0,318.
c) Jaka moc cieplna wydziela się w żarówce w przypadku kąta θF = 0°.
W celu uproszczenia obliczeń przyjąć, iż rezystancja żarówki ma stałą wartość.
Rozwiązanie zadania 5
a) Obliczamy wartość napięcia maksymalnego żarówki:
Em  2  En  2  110 V  156 V
(1)
Wartość napięcia skutecznego wynosi:
Esk  0,5  Em  0,5  156  78 V
(2)
Rezystancję żarówki można wyznaczyć równania:
RL 
U 2 1102

 121 
P
100
(3)
W związku z tym:
E
78
I sk  sk 
 0,64 A
RL 121
E
156
Im  m 
 1,29 A
RL 121
(4)
b) Obliczamy wartość średnią napięcia żarówki:
Eśr  0,318  Em  0,318  156  49,6 V
(5)
Prąd średni płynący przez żarówkę będzie miał wartość:
E
49,6
(6)
I śr  śr 
 0,41 A
RL
121
c) W przypadku przebiegu sinusoidalnego wyprostowanego dwupołówkowo w
warunkach pełnego przewodzenia moc skuteczna wynosi 100 W. W przypadku
przebiegu jednopołówkowego przy kącie θF = 0° moc wynosi połowę mocy przebiegu
dwupołówkowego, czyli 50 W.