Ćwiczenie nr 8 (Wyznaczanie wspułczynnika tarcia statycznego

Ćwiczenie nr 8 (Wyznaczanie wspułczynnika tarcia statycznego).DOC
(285 KB) Pobierz
Wykonano
Nazwisko:
Fleszar
Imię:
Mariusz
Kierunek:
Fizyka Techniczna 19.01.2012
Data
Podpis
Oddano
Data
Podpis
Rok studiów: I
Ćwiczenie
Nr.
8
Temat:
Wyznaczanie współczynnika tarcia statycznego.
Wstęp:
Siłę, z jaka oddziaływują na siebie dwa stykające sie ciała i która przeciwstawia się ich
względnemu ruchowi, nazywamy siłą tarcia. Siła tarcia ma kierunek styczny do powierzchni
zetknięcia, działa na każde z ciał i ma zwrot przeciwny do zwrotu jego prędkości względem drugiego
ciała. Źródłem siły tarcia są oddziaływania między atomami lub cząsteczkami ciał stykających
się. Jeżeli ciała nie przesuwają sie względem siebie, to występującą siłę tarcia nazywamy siłą tarcia
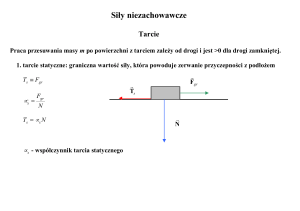
statycznego. Jej wartość maksymalna równa jest najmniejszej wartości siły zewnętrznej, która po
przyłożeniu do ciała spowoduje jego ruszenie. Jeżeli ciała poruszają sie względem siebie, to miedzy
ich powierzchniami działają siły tarcia kinetycznego. W tym ćwiczeniu badamy tarcie statyczne. Siła
tarcia statycznego nie zależy od wielkości powierzchni styku i jest proporcjonalna do siły reakcji
normalnej, która jest równa sile nacisku. Stosunek maksymalnej siły tarcia statycznego Tsmax i siły
reakcji R nazywamy współczynnikiem tarcia statycznego:
Należy pamiętać, ze siła tarcia i siła reakcji działają w kierunkach wzajemnie prostopadłych. Wartość
współczynnika tarcia zależy od rodzaju materiałów, chropowatości powierzchni, obecności
zanieczyszczeń lub warstwy tlenków.
Ponadto tarcie to całość zjawisk fizycznych towarzyszących przemieszczaniu się względem siebie
dwóch ciał fizycznych (tarcie zewnętrzne) lub elementów tego samego ciała (tarcie wewnętrzne) i
powodujących rozpraszanie energii podczas ruchu. Tarcie zewnętrzne występuje na granicy dwóch
ciał stałych. Tarcie wewnętrzne występuje przy przepływie płynów, jak i deformacji ciał stałych.
Podział tarcia zewnętrznego:
1) Tarcie ślizgowe:
Inaczej tarcie suwne; tarcie występujące na styku dwóch ciał stałych (jest tarciem zewnętrznym),
gdy ciała przesuwają się względem siebie lub gdy ciała spoczywają względem siebie a istnieje siła
dążąca do przesunięcia ciał. Tarcie ślizgowe jest zjawiskiem powszechnym i występuje zawsze, gdy
styk ciał przenosi siłę nacisku, odpowiada ono za wiele zjawisk, występuje w większości urządzeń
mechanicznych. Jeżeli ciała pozostają w spoczynku względem siebie, to tarcie nazywane jest tarciem
statycznym (spoczynkowym), a siła - siłą tarcia statycznego. Gdy ciała poruszają się względem siebie
to tarcie nazywa się tarciem ruchowym (kinetycznym, dynamicznym), a siła - siłą tarcia kinetycznego.
W ogólności dokładne wyjaśnienie przyczyn i wielkości siły tarcia jest trudne i nie jest dokładnie
poznane.
2) Tarcie toczne
Nazywane również oporem toczenia; opór ruchu występujący przy toczeniu jednego ciała po drugim.
Występuje np. pomiędzy elementami łożyska tocznego, między oponą a nawierzchnią drogi. Zwykle tarcie
toczne jest znacznie mniejsze od tarcia ślizgowego występującego między ciałami stałymi, dlatego toczenie
jest częstym rodzajem ruchu w technice. Tarcie toczne występuje na granicy dwóch ciał i dlatego jest
sklasyfikowane, jako tarcie zewnętrzne.
Maksymalna siła tarcia statycznego jest równa najmniejszej sile, jaka należy przyłożyć do ciała,
aby je ruszyć z miejsca. Maksymalna siła tarcia działająca między dowolna parą suchych
niepokrytych żadnych smarem) powierzchni podlega dwóm prawom empirycznym:
a) jest ona w przybliżeniu niezależna od wielkości powierzchni zetknięcia w bardzo szerokim zakresie;
b) jest proporcjonalna do siły normalnej tzn. siły, jaką jedna powierzchnia naciska na drugą.
Siła nacisku jest zawsze prostopadła do powierzchni zetknięcia. Powstaje ona w wyniku sprężystej
deformacji ciał w pobliżu punktów zetknięcia, ponieważ rzeczywiste ciała nigdy nie są doskonale
sztywne. W przypadku ciała leżącego lub ślizgającego się po poziomym stole wartość siły nacisku
jest równa ciężarowi ciała. Wynika to z faktu, że ciało nie ma pionowego przyśpieszenia, a więc stół
musi wywierać na to ciało siłę przyciągania ziemskiego, czyli równą ciężarowi ciała.
Stosunek maksymalnej wartości siły tarcia statycznego do wartości siły normalnej nazywamy
współczynnikiem tarcia statycznego dla danych powierzchni. Jeśli Fs przedstawia wartość
bezwzględną siły tarcia statycznego, możemy napisać
gdzie:
µs – współczynnik tarcia statycznego
N – wartość bezwzględna siły normalnej
Znak równości odnosi się wyłącznie do przypadku, gdy Fs ma maksymalna wartość.
Siła tarcia kinetycznego Fk, między dwiema suchymi powierzchniami podlega tym samym
dwóm prawom:
a) jest ona w przybliżeniu niezależna od wielkości powierzchni zetknięcia
b) jest proporcjonalna do siły normalnej.
Siła tarcia kinetycznego nie zależy ponadto od względnej prędkości poruszania się po powierzchni.
Stosunek wartości tarcia kinetycznego do wartości siły normalnej nazywany jest
współczynnikiem tarcia kinetycznego. Jeśli Fk oznacza wartość bezwzględna siły tarcia kinetycznego,
to
gdzie: µk – współczynnik tarcia kinetycznego
Zarówno µk jak i µs są stałymi bezwymiarowymi, ponieważ każde z nich jest stosunkiem wartości
bezwzględnych dwóch sił.
Zwykle dla danej pary powierzchni
. Wartość współczynnika tarcia zależy od wielu
czynników, takich jak rodzaje materiałów, obróbka powierzchni, warstwy powierzchniowe,
temperatura oraz stopień zanieczyszczenia powierzchni.
Rozważmy przypadek ciała zsuwającego się po równi pochyłej nachylonej pod kątem α do
poziomu. Zwiększając stopniowo kąt nachylenia równi stwierdzamy, że przy kącie równym αs klocek
zaczyna się ześlizgiwać.
W –ciężar kocka
N – siła normalna, jaką równia pochyła działa na klocek
Fs – styczna do powierzchni zetknięcia siła tarcia wywierana przez równię
Ponieważ klocek jest w spoczynku, więc
skąd otrzymujemy
Wiadomo, że
. Jeśli będziemy bardzo wolno zwiększać kąt nachylenia, aż do momentu,
gdy klocek zacznie się zsuwać (dla α = αs), to będziemy mogli przyjąć, że
to do równań otrzymamy
. Podstawiając
oraz
skąd
Współczynnik tarcia statycznego jest tym samym równy tangensowi kąta nachylenia powierzchni
równi, przy którym klocek zaczyna się zsuwać.
1. Cel ćwiczenia:
 Praktyczne zapoznanie się z metodą wyznaczania współczynnika tarcia statycznego .
 Wyznaczanie wartości współczynnika tarcia statycznego dla kilku rodzajów powierzchni
trących.
 Porównanie wartości współczynników otrzymanych dwiema metodami.
2. Przebieg ćwiczenia:
1.
Wyznaczyć współczynnik fs tarcia statycznego na podstawie pomiaru kąta nachylenia α (rys.
1), przy którym ciało umieszczone na równi zaczyna się samorzutnie zsuwać.
fs= tg α
Uwaga: zbadać powtarzalność wyników pomiarów kąta α w serii próbnej 3-4 pomiarów. Jeśli to okaże się
konieczne wykonać serię kilkunastu pomiarów tego kąta.
Wyznaczyć współczynnik fs tarcia statycznego drugą metodą mierząc bezpośrednio siłę tarcia statycznego FT.
(rys. 2).
Siłę nacisku FN można otrzymać na podstawie pomiaru masy ciała na wadze laboratoryjnej.
Uwaga: zbadać powtarzalność wyników pomiarów FT postępując analogicznie jak przy pomiarach kąta α w
punkcie 1.
3.
Określić niepewności pomiarowe i porównać wyniki otrzymane dwiema metodami.
4.
Pomiary współczynnika tarcia statycznego fs należy wykonać dla kilku rodzajów powierzchni
trących.
Rys.1
Rys.2
3. Wykaz narzędzi:
Waga laboratoryjna, klocki o różnych powierzniach trących, ruwnia pochyła o zmiennym kącie,
cztery powierzchnie trące, odważniki.
4. Tabela wyników pomiarów:
a) Równia pochyła:
Klocek (1)
...
(drewno)
Plik z chomika:
fleshman
Inne pliki z tego folderu:

Łącza telekomuniakacyjne.pdf (1132 KB)
Ćwiczenie nr 7 (Badanie kształtu linii emisyjnej lasera półprzewodnikowego).docx (1291
KB)
 Ćwiczenie nr 1 (Badanie własności promieniowania laserowego lasera He-Ne).docx (942
KB)
 Wyznaczenie sprawności modułu fotowoltaicznego.docx (1903 KB)
 Ćwiczenie nr 67 (Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjnej).docx (2288
KB)

Inne foldery tego chomika:


E-book
Galeria
 Muzyka (music)
 Prywatne
 zachomikowane
Zgłoś jeśli naruszono regulamin





Strona główna
Aktualności
Kontakt
Dział Pomocy
Opinie


Regulamin serwisu
Polityka prywatności
Copyright © 2012 Chomikuj.pl