Funkcja rozkładu Fermiego

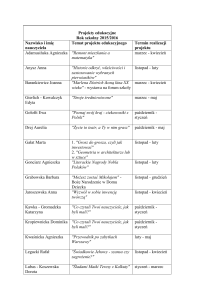
Metale
Najczęstsze struktury krystaliczne :
heksagonalna,
objętościowo centrowana
powierzchniowo centrowana
listopad 2002
Slide
1
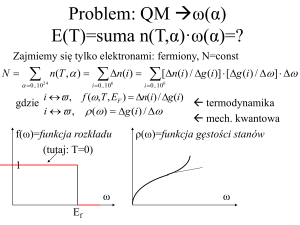
Funkcja rozkładu Fermiego-Diraca
f (E) 

Dla T = 0 K,
1
e  E  E F  kT  1
f(E) =

1
E < EF
0
E > EF
W T=0 zapełnione są wszystkie stany o
energiach poniżej EF

Dla dowolnej temperatury prawdopodobieństwo zapełnienia stanu o
energii EF wynosi 0.5
f(E) = 0.5 dla E = EF
listopad 2002
Slide
3
Gęstość stanów
g(E)dE jest liczbą stanów w jednostce objętości
mających energię od E do E+dE
•
• gęstość stanów g(E) dana jest wyrażeniem
g (E ) 
2pm
8
h

3
3
2
1
E
2
W 1cm3 miedzi liczba stanów o energiach od 5.0 eV do 5.5 eV
wynosi:
N ~ g(E)V ΔE 
8
3
2p (9.1x10 31kg) 2
(6.63 x10 34 J .s )3
1
(1x10 6 m 3 )(5.25 x1.6 x10 19 J ) 2
x (0.5 x1.6 x10 19 J ) ~ 8 x10 21
listopad 2002
Slide
4
Funkcja rozkładu Fermiego - Diraca



W danym stanie kwantowym nie może być dwu elektronów opisanych
tym samym zestawem liczb kwantowych.
W danym stanie mogą być dwa elektrony różniące się spinem, jeden o
spinie +1/2 i drugie ze spinem -1/2.
W konsekwencji w T=0 K elektrony
obsadzają kolejno stany o coraz to
wyższej energii aż do pewnej energii
maksymalnej, którą nazywamy energią
Fermiego EF.
listopad 2002
Slide
5
Funkcja rozkładu Fermiego - Diraca
Ilość elektronów w jednostce objętości zajmujących stany od energii
E=0 do EF
16 2p m 3 / 2 3 / 2
n   g ( E )dE 
EF
3
3h
0
EF
skąd
2
h 3 
EF 
 n
8m  p 
2
3
Dla miedzi =8.4x1028 m-3, a energia Fermiego EF=7.0 eV
listopad 2002
Slide
6
Wartość średnia energii elektronu w metalu
EF
3
 E   g ( E ) E dE  EF
5
0
Energia Fermiego dla miedzi: EF=7.0 eV, energia średnia 4.2 eV
Dla T=300 K 3/2kT=0.039 eV
Ze wzrostem temperatury elektrony z poziomów leżących poniżej EF
przechodzić będą na wyższe poziomy energetyczne. Prawdopodobieństwo
tego, że na poziomie o energii E znajduje się elektron określa funkcja
rozkładu Fermiego-Diraca
listopad 2002
Slide
7
Gęstość stanów zajętych elektronami

no(E)dE jest ilością elektronów w jednostce objętości o energiach
od E do E+dE w stanie równowagi w temperaturze T.
8 2pm
no ( E )  g ( E ) f ( E ) 
h3
listopad 2002
3
2
E
1
2
e  E  E F  kT  1
Slide
8
Gęstość stanów zajętych elektronami

Ze wzrostem temperatury elektrony z
poziomów
leżących
poniżej
EF
przechodzić będą na wyższe poziomy
energetyczne. W procesie tym bierze
udział
jedynie
niewielka
ilość
elektronów o energiach w pobliżu
energii EF.
Dla T=1200K 3/2kT=154.8meV

Prędkość elektronów o energiach bliskich EF

Energia potencjalna elektronu w metalu U=0 więc
E K  1 mv F2
2
Dla miedzi EF  7eV czyli vF  1.6  106 m / s
Dla porównania w gazie klasycznym dla T=1200K <v>=2.3x105 m/s
listopad 2002
Slide
9
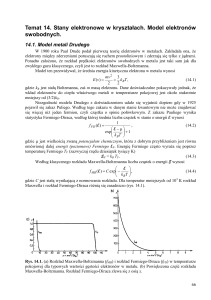
Struktura pasmowa ciał stałych
Dwa atomy
listopad 2002
Sześć atomów
Ciało stałe
N1023 atomów/cm3
Slide
10
Struktura pasmowa ciał stałych
listopad 2002
Slide
11
Struktura pasmowa ciał stałych
częściowo zapełnione
pasmo
pasma energetyczne Na



listopad 2002
Sód - orbitale 1s, 2s and 2p są całkowicie
zapełniane elektronami a 3s ma tylko jeden
elektron.
Pasmo powstałe ze stanów 3s będzie zapełnione do
połowy.
Dobry przewodnik - metal
Slide
12
listopad 2002
Slide
13
Funkcja rozkładu Fermiego-Diraca
T>0
E
funkcja
Fermiego
Pasmo przewodnictwa
(częściowo zapełnione)
EF
E=0
Dla T = 0, wszystkie stany o energii poniżej energii Fermiego EF są
zapełnione elektronami, a wszystkie o energiach powyżej EF są puste.
Dowolnie małe pole elektryczne może wprawić w ruch elektrony z poziomu
EF dostarczając im energii DE=eFEx prowadząc do bardzo dużego
przewodnictwa elektrycznego.
w temperaturach T > 0, elektrony są termicznie wzbudzane do stanów o
energiach powyżej energii Fermiego.
listopad 2002
Slide
14
Mg
listopad 2002
Slide
15
Struktura pasmowa ciał stałych
listopad 2002
Slide
16
Struktura pasmowa ciał stałych
Przewodnik
listopad 2002
Izolator
Półprzewodnik
Slide
17
Struktura pasmowa ciał stałych- półprzewodniki
listopad 2002
Slide
18
Przewodnictwo samoistne
ln()
1/T
 s   0s e
listopad 2002
 Eg / 2kT
Slide
19
Przewodnictwo domieszkowe
ln()
 d   0d e
 Ed / kT
1/T
listopad 2002
Slide
20
listopad 2002
Slide
21
Zależność przewodnictwa od temperatury
ln()
 s   0s e
 Eg / 2kT
 d   0d e  Ed / kT
1/T
listopad 2002
Slide
22