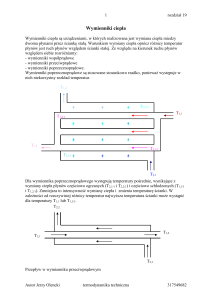
WYMIANA CIEPŁA PRZY ZMIANACH STANU
SKUPIENIA
WYKŁAD 8
Dariusz Mikielewicz
Politechnika Gdańska
Wydział Mechaniczny
Katedra Techniki Cieplnej
Wstęp
Szczególnym przypadkiem konwekcyjnej wymiany ciepła są zagadnienia, w których
występuje więcej niż jedna faza tego samego czynnika. Doprowadzone ciepło
powoduje przejście jednej fazy w drugą na granicy rozdziału faz, bez zmiany
temperatury. Mamy więc do czynienia z przejściem fazy parowej w fazę ciekłą
zwanym kondensacją bądź z przejściem odwrotnym, tzn. fazy ciekłej w parową,
zwanym wrzeniem. Jednakże zagadnienia te są znacznie bardziej skomplikowane
niż zagadnienia konwekcji w jednej fazie. Ich opis matematyczny wymaga zatem
opisu zarówno obu faz, jak i zjawisk zachodzących na granicy ich rozdziału.
Z tego też względu istniejące teorie podają
na ogół uproszczony opis zagadnień i
wymagają weryfikacji eksperymentalnej.
Zagadnienia te, spotykane w energetyce,
technologii chemicznej i w szeregu innych
dziedzin współczesnej techniki, mają
ogromne znaczenie praktyczne. Przemiany
jednej fazy w drugą mogą zachodzić
zarówno na ściance jak i wewnątrz fazy,
zwykle jednak spotykanym w praktyce jest
pierwszy z przypadków.
Wymiana ciepła podczas kondensacji pary
Jeżeli temperatura powierzchni jest niższa od temperatury nasycenia pary, to para
kondensuje się na tej powierzchni, przy czym rozróżniamy kondensację kroplową i
błonową.
Pierwsza z nich, a zatem kondensacja kroplowa to proces, podczas którego na
powierzchni powstają krople kondensatu. Można ją wywołać na powierzchni nie
zwilżonej przez ciecz lub też przez sztuczne pokrycie powierzchni odpowiednimi
warstwami np. tłuszczu. Druga z nich - kondensacja błonowa - to proces
kondensacji, podczas którego na powierzchni powstaje film cieczy. Kondensacja taka
zachodzi na powierzchni, która może być dobrze zwilżona przez ciecz, przy czym w
praktyce na ogół spotyka się kondensację błonową oraz mieszaną.
Kondensacja kroplowa charakteryzuje się bardzo wysokimi współczynnikami
przejmowania ciepła, znacznie wyższymi niż kondensacja błonowa.
Podczas kondensacji błonowej grubość filmu cieczy rośnie na skutek odprowadzania
ciepła od ścianki i pod wpływem sił ciężkości film ten zaczyna spływać w dół. Ruch
kondensatu jest laminarny, po czym przy dalszym wzroście grubości filmu przechodzi
w laminarny falowy, a następnie w turbulentny.
Wstęp
Ciepło przechodząc poprzez film cieczy do ścianki pokonuje opór cieplny przejścia
fazy parowej w ciekłą oraz opór cieplny kondensatu. Wobec tego całkowity opór
cieplny R przejścia strumienia cieplnego można zapisać w postaci zależności
R=
Ti − Tw 1
= = R L + Ri ,
q
α
RL - opór cieplny filmu cieczowego,
Ri - opór cieplny przejścia fazy parowej w ciekłą,
Ti - temperatura powierzchni rozdziału faz,
Tw - temperatura ścianki,
q - gęstość strumienia cieplnego,
α - współczynnik przejmowania ciepła podczas kondesacji
Wstęp
Opór cieplny Ri powoduje uskok temperatury na powierzchni rozdziału faz
Tv − Ti .
Proces kondensacji można rozpatrywać na gruncie molekularnej budowy materii.
Zależność na opór przejścia fazy parowej w ciekłą można przedstawić w postaci
R =
i
2−k
2k
2πR T − T
P
P
h
−
T
T
v
lv
v
i
i
v
i
R
-
indywidualna stała gazowa pary,
hlv
-
ciepło parowania (kondensacji),
Tv
-
temperatura fazy parowej,
Ti
-
temperatura na powierzchni rozdziału faz,
Pv
-
ciśnienie fazy parowej,
Pi
-
ciśnienie na powierzchni rozdziału faz,
k
-
współczynnik kondensacji.
Wstęp
Z powyższej zależności wynika, iż opór cieplny przejścia fazy parowej w ciekłą
zależy od ciśnienia Pv, współczynnika k oraz gęstości strumienia ciepła q, którego
zmiana wiąże się ze zmianą różnicy Tv-Ti.
Jak wykazują obliczenia, tym większy jest uskok temperatury na granicy rozdziału
faz, im mniejsze wartości współczynnika k oraz mniejsze ciśnienie pary.
Doświadczenia przeprowadzone przy kondensacji błonowej dla czystej pary wodnej
przy ciśnieniu p > 0,1 bara wykazały, że uskok ten jest praktycznie bliski zeru.
Opór cieplny filmu RL zależy od charakteru przepływu filmu. W przypadku ruchu
laminarnego ciepło przez film przenoszone jest na drodze przewodnictwa,
natomiast w przypadku ruchu turbulentnego dodatkowo na drodze konwekcyjnej.
Przejścia ruchu laminarnego w turbulentny dla filmu wyznacza się przy pomocy
liczby Reynoldsa opisanej następującą zależnością
wδ
Re =
,
νL
gdzie w jest to średnia prędkość filmu dla określonej współrzędnej wzdłuż kierunku
spływu kondensatu, δ to grubość kondensatu w tym miejscu, zaś νL to współczynnik
lepkości kinematycznej filmu.
Wstęp
Dane doświadczalne wskazują, że krytyczna liczba Reynoldsa zmienia się od 60 do
500. W praktyce dla powierzchni pionowych przyjmuje się liczbę Rekr = 400
Ruch laminarny filmu może przechodzić w falowy, wówczas to proces wymiany
ciepła jest dość złożony. Z badań Kapicy wynika, że średnia grubość filmu
zafalowanego jest mniejsza niż średnia grubość filmu laminarnego, co powoduje,
że współczynniki przejmowania ciepła dla falowego ruchu kondensatu są wyższe
niż dla laminarnego. Ruch falowy kondensatu występuje po przekroczeniu wartości
liczby Reynoldsa
Re ≥ Re fal
⎛
⎞
σ
⎟
= 0.56⎜⎜
1/ 3 4 / 3 ⎟
⎝ ρL g ν L ⎠
3 / 11
,
Rozróżnia się także kondensację pary nieruchomej oraz pary ruchomej, przy której
ruchu na granicy rozdziału faz powstają siły tarcia mogące spowodować
zatrzymywanie bądź przyspieszanie ruchu filmu, w zależności od kierunku ruchu
kondensatu i pary. W efekcie może to prowadzić do zmiany grubości filmu, a zatem
także jego oporu cieplnego.
Wstęp
Z reguły para podczas kondensacji zawsze posiada pewną prędkość, która wynika z
faktu zamiany masy pary na masę cieczy. Jeśli zjawisko kondensacji następuje w
dużej objętości, para przemieszcza się prostopadle do ścianki ze średnią prędkością:
w =
v
q
hρ
lv
v
q
-
średnia gęstość strumienia ciepła,
hlv
-
ciepło kondensacji,
ρv
-
gęstość pary.
Prędkość pary nie wpływa jednak istotnie na sam proces wymiany ciepła, wobec
czego jeśli para posiada tylko tę prędkość to uważa się ją za nieruchomą.
Zwykle w zagadnieniach teoretycznych zakłada się dodatkowo, że para jest
nasycona. Kondensacja pary mokrej i przegrzanej jest bardziej złożona.
Kondensacja na pionowej ścianie
Rozważamy kondensację pary nasyconej na pionowej
ściance, wprowadzając następujące założenia
upraszczające (teoria Nusselta (1916)):
- ruch filmu jest laminarny,
- gradient ciśnienia oraz siły bezwładności filmu są
zaniedbywalne,
- prędkość kondensatu przy ściance równa jest zeru,
- temperatura na powierzchni rozdziału faz równa jest
temperaturze nasycenia, Ti = Ts,
- ruch pary jest pomijalny,
- temperatura ścianki jest stała, Tw = const,
- własności fizyczne filmu są stałe i niezależne od
temperatury,
- wpływ napięcia powierzchniowego jest zaniedbywalny,
- konwekcyjne przenoszenie ciepła oraz przewodnictwo
cieplne w kierunku wzdłużnym są zaniedbywalne.
kondensat
Kondensacja na pionowej ścianie
Warunki brzegowe:
y = 0 , T = Tw
,
wx = 0
y = δ x , T = Ts
⎛∂ wx
, ⎜⎜
⎝ ∂y
⎞
⎟⎟ = 0,
⎠ gr
Przy powyższych założeniach proces wymiany ciepła będzie opisany równaniami:
- ruchu, zgodnie z zależnością
- energii, zgodnie z zależnością
⎛ ∂ 2 wx ∂ 2 wx
ν L ⎜⎜
+
2
∂
∂ y2
x
⎝
d 2T
=0
2
dy
⎞
⎟⎟ = g
⎠
Kondensacja na pionowej ścianie
Rozwiązanie równania energii przy warunkach brzegowych :
dT Ts − Tw
=
,
dy
δx
pozwala na obliczenie współczynnika przejmowania ciepła danego wyrażeniem
dT
λ
dy
= .
αx =
Ts − Tw δ x
λL
Jako że pomijamy wpływ sił bezwładności, które mogłyby powodować zmianę
prędkości w kierunku osi x, równanie ruchu może być uproszczone przez
pominięcie w nim członu i po jego scałkowaniu przy powyższych warunkach
brzegowych, otrzymujemy paraboliczny profil prędkości dany wyrażeniem
⎛ ∂ 2 wx ∂ 2 wx
ν L ⎜⎜
+
2
2
∂
∂
x
y
⎝
⎞
⎟⎟ = g
⎠
g ⎛
y2 ⎞
⎜δ x y −
⎟.
wx =
ν L ⎜⎝
2 ⎟⎠
Kondensacja na pionowej ścianie
Średnią wartość prędkości filmu kondensatu określić możemy z zależności:
δx
1 δ x2
wx =
w x dy = g
δ x ∫0
3 νL
1
natomiast strumień kondensatu mx, przechodzący przez przekrój w odległości x od
początku ścianki, przypadający na 1 m szerokości ścianki, można przedstawić jako:
m x = wx ρ Lδ x =
1 ρL 3
g
δx.
3 νL
Z kolei zmianę ilości kondensatu na odcinku dx określimy w postaci
∂m x
gρ L δ x2
dm x =
dδ x =
dδ x .
∂δ x
νL
Kondensacja na pionowej ścianie
dQ = h dm
λ
lv
x
Przyrost dmx spowodowany jest odprowadzaniem ciepła dQ z powierzchni 1×dx:
dQ = h dm =
lv
x
h gρ δ
lv
L
ν
2
x
dδ ,
x
L
gdzie hlv jak poprzednio jest ciepłem kondensacji. Wyrażając teraz ciepło dQ za
pomocą gęstości strumienia ciepła q uzyskujemy
dQ = qdx ⋅ 1 =
λL
(Ts − Tw )dx
δx
Kondensacja na pionowej ścianie
Porównując prawe strony powyższych równań otrzymujemy różniczkowe
równanie opisujące zmienność grubości filmu kondensatu δx ze współrzędną x
h gρ δ
lv
L
ν
2
x
dδ =
x
L
λ
(T − T )dx.
δ
L
s
w
x
Po scałkowaniu powyższego równania i przyjęcia warunku
x = 0 , δx = 0
skąd stała całkowania C = 0, a grubość filmu kondensatu
δ =
x
4λ ν (T − T )x
.
hρg
L
4
L
s
lv
w
L
Lokalna wartość współczynnika przejmowania ciepła
hρλg
λ
.
α = =
4ν (T − T )x
δ
3
L
x
x
lv
4
L
L
L
s
w
Średnia wartość współczynnika przejmowania ciepła na długości l
hρλg
1
4
α = ∫ α dx =
.
l
3 4ν (T − T )l
l
3
lv
L
L
x
0
L
s
w
Kondensacja na pionowej ścianie
Powyższa zależność może być przedstawiona w postaci bezwymiarowej
(Nu ) = 4 ⎡⎢ 1 (Ga )(Pr )K ⎤⎥
3 ⎣4
⎦
(N u ) = αl
λl
(Ga ) =
gl 3
ν L2
1
4
= 0.943[(Ga )(Pr )K ]
1
K=
4
h
c ΔT
lv
p ,L
Niektórzy następcy Nusselta rozważali powyższy problem z uwzględnieniem
nieliniowego profilu temperatury, rozwiązując przy tym warunku równanie energii.
Inni natomiast uwzględniali siły bezwładności. Jednakże, mimo iż rozwiązania te
były dokładniejsze od uzyskanych przez Nusselta, wprowadziły one niewiele zmian
do pierwotnego rozwiązania (nusseltowskiego).
Należy dodać, iż teoria Nusselta odnosząca się do płyty pionowej stworzyła
podstawy rozwiązania zagadnienia kondensacji na płytach nachylonych oraz na
rurze.
Turbulentny ruch kondensatu
Przy turbulentnym przepływie kondensatu wymiana ciepła w porównaniu z
ruchem laminarnym intensyfikuje się. Przy ruchu laminarnym bowiem ciepło
przenosiło się tylko na drodze przewodnictwa cieplnego, natomiast przy ruchu
turbulentnym, dodatkowo poprzez konwekcję.
Jak wiadomo, w ruchu turbulentnym strumień cieplny oraz naprężenie styczne w
dowolnym przekroju równoległym do ścianki mogą być opisane równaniami, które
uwzględniają fakt, że przy ruchu turbulentnym przenoszenie ciepła i pędu odbywa
się nie tylko na drodze molekularnej, ale i dzięki turbulentnym pulsacjom.
ε ⎤ dw
⎡
τ = μ ⎢1 + (Pr ) H ⎥ x
ν ⎦ dy
⎣
ε ⎤ dT
⎡
q = λ ⎢1 + (Pr ) T ⎥
ν ⎦ dy
⎣
Przyjmuje się εT = εH = ε, gdzie εH jest dyfuzyjnością pędu, a εT - dyfuzyjnością ciepła.
Zjawisko przejścia ciepła przez kondensat zachodzi praktycznie przy stałym strumieniu
cieplnym, w odróżnieniu od przejścia ciepła w cieczy jednofazowej w rurze, gdzie
strumień cieplny zmienia się od wartości maksymalnej na ściance do zerowej w osi rury.
Turbulentny ruch kondensatu
Lokalny współczynnik przejmowania ciepła może być określony po scałkowaniu
zależności opisującej strumień ciepła, w której przyjmuje się, że własności
fizyczne dotyczą kondensatu
Ts
δ
Tw
0
∫ dT = Ts − Tw = q ∫
dy
⎡
λ L ⎢1 + (Pr) L
⎣
ε ⎤
ν L ⎥⎦
skąd lokalna wartość współczynnika przejmowania ciepła jest określona jako
α=
1
dy
q
=δ
Ts − Tw
∫
0
⎡
λ L ⎢1 + (Pr) L
⎣
.
ε ⎤
ν L ⎥⎦
Łabuncew przeprowadził obliczenia lokalnego współczynnika przejmowania ciepła. Ich
wyniki aproksymował w przedziałach 1 ≤ (Pr ) ≤ 25 , 1.5 ≤ Re ≤ 6.9 ⋅ 10 4
L
α
λL
⎛ ν L2
⎜⎜
⎝ g
⎞
⎟⎟
⎠
1
3
= 0.6325(Pe )
0.25
(Pr )0.5
(Re ) = w δ
νL
=
m
μL
(Re) = α ΔTl = (Nu )
(Pr )K
rμ L
Turbulentny ruch kondensatu
Lokalny współczynnik przejmowania ciepła może być określony po scałkowaniu
zależności opisującej strumień ciepła, w której przyjmuje się, że własności
fizyczne dotyczą kondensatu
Ts
δ
Tw
0
∫ dT = Ts − Tw = q ∫
dy
⎡
λ L ⎢1 + (Pr) L
⎣
ε ⎤
ν L ⎥⎦
skąd lokalna wartość współczynnika przejmowania ciepła jest określona jako
α=
1
dy
q
=δ
Ts − Tw
∫
0
⎡
λ L ⎢1 + (Pr) L
⎣
.
ε ⎤
ν L ⎥⎦
Łabuncew przeprowadził obliczenia lokalnego współczynnika przejmowania ciepła. Ich
wyniki aproksymował w przedziałach 1 ≤ (Pr ) ≤ 25 , 1.5 ≤ Re ≤ 6.9 ⋅ 10 4
L
α
λL
⎛ ν L2
⎜⎜
⎝ g
⎞
⎟⎟
⎠
1
3
= 0.6325(Pe )
0.25
(Pr )0.5
(Re ) = w δ
νL
=
m
μL
(Re) = α ΔTl = (Nu )
(Pr )K
rμ L
Kondensacja na rurach poziomych
Rozwiązanie zagadnienia kondensacji dla płyty pozwala na rozwiązanie
zagadnienia kondensacji dla rury poziomej.
Średni współczynnik przejmowania ciepła podczas kondensacji dla rury
poziomej, dla przypadku, gdy temperatura ścianki rury jest stała Tw = const
α = 0.728
4
λ ρ gh
lv
L
w
3
L
L
μ (T − T )d
s
W przypadku, gdy qw = const stała powyżej przyjmuje wartość 0.693.
W praktyce przemysłowej, z reguły mamy do czynienia z kondensacją zachodzącą na
pęczku rur w wymienniku. Proces wymiany ciepła jest tu bardziej złożony niż w
przypadku pojedynczej rury. Przestrzeń, w której zachodzi kondensacja jest
ograniczona, dlatego też na wymianę ciepła wpływa ruch pary. Ponadto, kondensat
ścieka z rurek położonych wyżej na rurki położone niżej, co powoduje zmianę grubości
warstwy kondensatu na rozpatrywanej rurce, a tym samym zmianę oporu cieplnego
kondensatu. Ze względu na zmienny opór cieplny kondensatu, związany także ze
zmiennym współczynnikiem przejmowania ciepła, zmienna jest również temperatura
ścianek poszczególnych rur, co stanowi dodatkową komplikację w analitycznej analizie
przejmowania ciepła w pęczku rur.
Wymiana ciepła podczas wrzenia
Przejście fazy ciekłej w parową następuje, gdy faza ciekła jest przegrzana, tzn.
gdy jej temperatura jest wyższa od temperatury nasycenia. Powstawanie fazy
parowej związane jest z istnieniem zarodków będących źródłami tworzenia się
fazy, takich jak zanieczyszczenia w cieczy, rozpuszczone gazy, cząstki
promieniowania bądź fluktuacje gęstości lub nierówności na ściance.
Wymiana ciepła podczas wrzenia
Analiza wykazała, iż praca tworzenia się pęcherzyków parowych jest mniejsza dla
nierówności powierzchni jak dla zarodków istniejących w objętości cieczy, stąd też
faza parowa tworzy się z reguły na ściance, do której doprowadza się ciepło.
Zagadnienia wrzenia, podobnie jak zagadnienia konwekcji w jednej fazie dzielą się
w ogólności na zagadnienia, przy których geometria przestrzeni i hydrodynamika
przepływu nie wpływa istotnie na proces wymiany ciepła, nazywane wówczas
wrzeniem w objętości oraz na zagadnienia, w których kształt przestrzeni i
hydrodynamika przepływu faz ma zasadniczy wpływ na wymianę ciepła, nazywane
wrzeniem w przepływie.
Ponadto, przy małych strumieniach cieplnych, a zatem małych przegrzaniach cieczy
wrzenie ma charakter pęcherzykowy, zaś przy dużych strumieniach cieplnych, czyli
dużych przegrzaniach cieczy, zamiast pęcherzyków parowych na ściance tworzy się
błona parowa i takie wrzenie nazywa się wrzeniem błonowym.
Rozróżnia się także wrzenie przechłodzone, które ma miejsce gdy temperatura
cieczy w pewnej odległości od ścianki jest niższa od temperatury nasycenia i wrzenie
nasycone, gdy temperatura cieczy w całej rozpatrywanej objętości jest równa albo
nieco wyższa od temperatury nasycenia.
Wrzenie pęcherzykowe
Przy przegrzaniu się cieczy na zarodkach znajdujących się na ściance zaczynają
tworzyć się pojedyncze pęcherzyki parowe i w miarę dalszego przegrzewanie cieczy
uaktywniają się kolejne zarodki, a więc pojawia się coraz więcej pęcherzyków na
jednostkę czasu przez zarodek, w wyniku czego pęcherzyki mogą się łączyć w
kierunku pionowym i poziomym przepływu. Dalszy wzrost przegrzania prowadzi do
utworzenia początkowo niestabilnej, a następnie stabilnej błony parowej.
Dla ustroju pojedynczych pęcherzyków parowych nie oddziaływujących wzajemnie
na siebie, najprostszego do analizy teoretycznej, określamy minimalne przegrzanie
cieczy (nadwyżka temperatury cieczy Tc względem temperatury nasycenia Ts), przy
którym może istnieć pęcherzyk parowy, wielkość odrywającego się pęcherzyka o
przyjętym dla uproszczenia kształcie sfery, częstość odrywania się pęcherzyków i ich
ruch w fazie ciekłej.
Wrzenie pęcherzykowe
Z warunku równowagi sił działających na pęcherzyk sferyczny, określonego
równaniem Laplace'a, wynika że różnica ciśnień między obu fazami jest
proporcjonalna do napięcia powierzchniowego
Δp = p v − p L =
pv
pL
σ
R
2σ
R
- ciśnienie fazy parowej,
- ciśnienie fazy ciekłej,
- napięcie powierzchniowe,
- promień pęcherzyka sferycznego,
Z powyższych zależności wynika, że temperatura nasycenia wewnątrz
pęcherzyka parowego TR,v będzie wyższa od temperatury nasycenia fazy ciekłej
lub temperatury nasycenia nad płaską powierzchnią Tv. Poszukiwane
przegrzanie będzie więc wynosić ΔT = TR,v-Tv
Nasycone wrzenie w objętości
para
ciecz
pęcherze
parowe
Ciało stałe
z
Wrzenie przechłodzone: Tl<Tsat
z
Wrzenie nasycone: Tl>Tsat
Rozważania fizyczne
z
z
q = hΔT
ΔT = Ts − T∞ ?
–
L? DT?
–
Skala długości pęcherzyków czy kapilarna
–
Nadwyżka temperatury
L=
ΔT = Ts − Tsat (P∞ )
Opis fenomenologiczny
ΔTe = (Ts − Tsat )
–
Nadwyżka temperatury
–
Ciepło parowania hlv
–
Napięcie powierzchniowe σ
–
Siły wyporu
(ρ l − ρ v )g
σ
g (ρl − ρ v )
Liczby bezwymiarowe
z
Liczba Nusselta
z
Liczba Prandtla
z
Liczba Jacoba
z
Liczba Bonda
z
Liczba bez nazwy
z
...
hL
k
ν μc p
Pr = =
α
k
c p ΔT
Ja =
h fg
Nu =
ρg(ρl − ρ v )L2
Bo =
σ
ρg(ρl − ρv )L3
μ2
Doświadczenie Nukiyamy
Para wodna, p=1 atm
Woda, Ts
drucik platynowy, q, ΔTe=Tw-Ts
Stanowisko Nukiyamy do pokazania procesu wrzenia
w objętości kontrolując strumień ciepła
Wizualizacja wrzenia w doświadczeniu Nukiyamy
Powstawanie pęcherzyków parowych
(a) obszar pojedynczych pęcherzyków
(b) obszar korków i kolumn (strugi parowe)
(c) Obszar wrzenia błonowego
Wyidealizowane strugi
parowe
Krzywa wrzenia– Nukiyama (1934)
Kontrolowany strumień ciepła
Kontrolowana temperatura
powierzchni
AB – Konwekcja jednofazowa
BC – Wrzenie pęcherzykowe
CF – Wrzenie przejściowe
FDE – Rozwinięte wrzenie błonowe
α
Krzywa wrzenia
Początek wrzenia (tzw. zerowy
kryzys wrzenia): przejście z 1F w
2F wrzenie pęcherzykowe
q
parowanie
q
wrzenie
kr
kr
-1
wrzenie blonowe
pęcherzykowe
P
K1
1
q
10
q
P
2
10
0
10
Kryzys wrzenia pierwszego
rodzaju: przejście wrzenia
pęcherzykowego w przepływ
błonowy
K2
2
1
10
2
1
Kryzys wrzenia drugiego rodzaju: odejście
od struktury błonowej i powrót do wrzenia
pęcherzykowego
Punkt Leidenfrosta
10
3
10 4
ΔT
Średnica oderwania z cen. nukleacji 0.1μm, q=10 kW/m2 i 50 kW/m2
Woda
Alkyl (8-16)
Początek wrzenia przechłodzonego, q=300kW/m2, Tf=40oC
Woda
Inny czynnik –
Habon B 530 ppm
Wrzenie nasycone na rurce. q=100 kW/m2
Woda
Alkyl
Konwekcja naturalna
z
q ~ ΔT
e
c
(c: 1/4~5/4)
z
c zależy od charakteru przepływu
z
Nie ma zależności liniowej pomiędzy q oraz ΔT - Dlaczego?
z
Dlaczego używamy liczby Nu podczas wrzenia?
z
Najczęściej używamy zależności dotyczących konwekcji naturalnej na
płycie (ogrzewanej)
Nu L ~ L δ th ~ Ra 1L 4
Wrzenie pęcherzykowe
z
Powstawanie pęcherzyka
–
Fluktuacje lokalnej gęstości molekularnej
–
Zarodki pęcherzyków
–
–
z
2σ
Pv = P∞ +
re
(niestabilne ekwilibrium)
Pv ≅ Psat (Tl ) ≅ Psat (Ts )
Obserwacje
–
q ′′ ~ ΔTea n b
(a=1.2, b=1/3)
–
n ~ ΔTed
(d=5~6)
Pv ≅ P∞
Wrzenie pęcherzykowe – Model Rohsenowa (1952) (1)
z
Założenie: Wymiana ciepła od powierzchni ogrzewanej do cieczy ⇒
powstawanie pęcherzyków ⇒ lokalna agitacja spowodowana cieczą płynącą w
śladzie odrywających się pęcherzyków ⇒ poprawa wymiany ciepła
z
Obserwacje eksperymentalne pokazują, że wpływ przechłodzenia cieczy na
wymianę ciepła zanika ze wzrostem gęstości strumienia ciepła
–
∴
q = α [T − T (P
W
Nu =
Lc
αL
c
k
sat
∞
)]
= A Re Pr = A Re (
n
1− r )
m
Lc
l
Lc
Pr (
1− s )
l
l
ρU L
ρU L
qL
Re =
=
=
μ
μ
hμ
l
c ,l
c
v
c ,v
c
c
Lc
l
l
lv
l
Wrzenie pęcherzykowe – Model Rohsenowa (1952) (2)
z
q′′
U =
ρh
Prędkości charakterystyczne
c ,v
v
lv
q′′
U =
ρh
c ,l
l
12
Characterystyczny wymiar pęcherzyka
⎤
⎡
3σ
Rb = ⎢
⎥
(
)
g
ρ
ρ
−
l
v ⎦
⎣
z
Characterystyczna długość
⎤
⎡
σ
Lc = ⎢
⎥
⎣ g (ρ l − ρ v )⎦
z
Średnica oderwania pęcherzyka wg Rosenowa
z
⎤
⎡
σ
Lc = C bθ ⎢
⎥
⎣ g (ρ l − ρ v )⎦
12
12
lv
Wrzenie pęcherzykowe – Model Rohsenowa (1952) (3)
z
Korelacja Rosenowa
q ′′
μ l h fg
⎤
⎡
σ
⎥
⎢
(
)
g
ρ
ρ
−
l
v ⎦
⎣
12
⎛ 1
=⎜
⎜C
⎝ f ,s
⎞
⎟
⎟
⎠
1r
⎛ c ΔTe
− s r ⎜ p ,l
Prl
⎜ h
fg
⎝
z
Incropera, (r=1/3 and s=n)
z
⎡ g (ρ − ρ )⎤ ⎛⎜ c ΔT ⎞⎟
q=μh ⎢
⎥⎦ ⎜ C h Pr ⎟
σ
⎣
⎝
⎠
Postać bezwymiarowa
12
l
l
p ,l
v
e
lv
n
s, f
Ja
αL
=
Nu =
λ
C Pr
2
c
3
l
nb
l
m
lv
l
⎞
⎟
⎟
⎠
3
1r
C f ,s =
2C bθ
A
Przepływ dwufazowy nieadiabatyczny
wymiana ciepła
Podczas przepływu:
¾ zmienia się masowa zawartość
fazy parowej x wzdłuż kanału,
przez konwekcję
α
.
.
.
¾ zmienia się stopień zapełnienia
kanału,
¾ zmienia się lokalny współczynnik
przejmowania ciepła przy ściance.
.
wrzenie
Przepływ fazy parowej
.
.
.
.
.
.
.
. .
.
.
. . .
.
.
.
. .
.
.
.
.
.
.
. .
. .
.
rozwinięte
przepływ mgłowy (ciecz
w postaci mgły w parze)
Przepływ pierścieniowy
(para z zawieszonymi kropelkami
cieczy wypełnia środek rury; cienka
warstwa cieczy na ściankach)
Przepływ korkowy
(duże pęcherze pary)
kierunek
doprowadzania ciepła
(promieniowy wzdłuż
długości kanału
Przepływ cieczy
o temperaturze nasycenia
( brak kondensacji
pęcherzyków pary )
q
wrzenie przechłodzone
Przepływ cieczy niedogrzanej
o temperaturze nasycenia przy
ściance (brak pęcherzyków pary)
wymiana ciepła
przez konwekcję
Przepływ cieczy niedogrzanej
do temperatury nasycenia
(brak pęcherzyków pary)
kierunek przepływu
Struktury przepływu dwufazowego
pęcherzykowy
korkowy
wirowo pierścieniowy
pierścieniowy
pierścieniowo - mgłowy
Struktury przepływu dwufazowego
pęcherzykowy
mgłowy
korkowy
pierścieniowy
Struktury przepływu dwufazowego, q=var
duża wartość
strumienia cieplnego
średnia wartość
strumienia cieplnego
mała wartość
strumienia
cieplnego
Kryzys wrzenia w przepływie
DNB (PWR)
Dryout (CANDU)
Niestabilność Taylora – różnica gęstości
Niestabilność K-H – różnica prędkości
Kryzys wrzenia w objętości
Niestabilność Kelvina-Helmholtza
λKH = f (σ , ρ l , ρ g , g )
Niestabilność Taylora
Kryzys wrzenia:
u2 > u1 → p2 < p1
Prowadzi do rozerwania się strug
λKH =
λT
2
Kryterium stabilnego
wrzenia błonowego
Początek wrzenia nasyconego
woda
Alkyl (8-16) C=300ppm
qw=90 kW/m2
m& = 5.7 kg / m 2 s
Rozwinięte wrzenie nasycone
woda
qw=90 kW/m2
m& = 5.7 kg / m s
2
Alkyl (8-16) C=300ppm
Kryzys wrzenia I rodzaju - dryout
woda
qw=90 kW/m2
m& = 5.7 kg / m s
2
Alkyl (8-16) C=300ppm
Korelacje empiryczne
Korelacje oparte na parametrze Martinellego Xtt
α
= a( X
α
⎛ 1 − x⎞
X tt = ⎜
⎟
⎝ x ⎠
tt
)
⎛ ρv ⎞
⎜ ⎟
⎝ ρl ⎠
0.5
⎛ μl ⎞
⎜ ⎟
⎝ μv ⎠
0.1
Dengler & Addoms: a=3.5 i b=-0.5,
b
tp
0.9
Guerrieri & Talty
l
α
= a ' [Bo + m( X
α
) ] Collier & Pulling:
b
tp
tt
Schrock & Grossman: a'=7400, b=0.66 & m = 0.00015
l
⎛α ⎞
α
⎟⎟
= 1 + ⎜⎜
α
⎝α ⎠
TPb
Pb
l
l
a=3.4 i b=-0.45
2
Kutateladze
a'=6700, b=0.66 & m = 0.00035
Istniejące metody
α TPB = S α Pb + F α cb
1.
Uogólnienie małej liczby indywidualnych danych eksperymentalnych
autorów w małym zakresie zmian parametrów
2.
Uogólnienie dużej liczby danych z wielu źródeł danych w dużym zakresie
zmian parametrów
Żadna ze znanych korelacji nie ma podstaw teoretycznych!
Oczekiwanie od korelacji uogólnionych
1.
Podstawy teoretyczne
2.
Dobre odwzorowanie WPC
3.
Prosta postać analityczna
Półempiryczna metoda wyznaczania WPC podczas wrzenia w przepływie
(Mikielewicz (1972))
•
Wrzenie w objętości
•
Konwekcyjna wymiana ciepła cieczy lub gazu
•
Adiabatyczny współczynnik oporu przepływu (R)
Wymiana ciepła z generacją pęcherzyków
Dysypacja energii w przepływie
ETPb = ETP + EPb
Zdefiniowanie odpowiednich członów prowadzi do wyrażenia
2
2
2
ξ TPb
= ξ TP
+ ξ Pb
Używając analogii między wymianą ciepła i pędu
2
2
2
α TPb
= α TP
+ α Pb
α TPb
=
α0
R
0 .8
⎛ α Pb
+ ⎜⎜
⎝ α0
α TP = R 0 .4α 0
⎞
⎟⎟
⎠
2
J. Mikielewicz (1972)
Modyfikacja korelacji - 2006
RM − S
α
f =
α
GO
1z
LO
⎡
⎞ ⎤
⎛1
1
= ⎢1 + 2⎜⎜ − 1⎟⎟ x ⎥ ⋅ (1 − x)1 / 3 + x 3
f 1z
⎢⎣
⎠ ⎥⎦
⎝ f1
μ c ⎛λ ⎞
⎜ ⎟
=
μ c ⎜⎝ λ ⎟⎠
G
pL
L
L
pG
G
α TPB
1 ⎛ α PB
0.76
⎜⎜
= RM − S +
α REF
1 + p ⎝ α REF
⎛ dp ⎞
⎜⎜ ⎟⎟
dp ⎠
⎝
f =
⎛ dp ⎞
⎜ ⎟
⎝ dz ⎠
3/ 2
GO
1
⎞
⎟⎟
⎠
2
⎛μ
= ⎜⎜
⎝μ
L
G
⎞
⎟
⎟
⎠
1/ 4
ρ
ρ
G
L
LO
P = a(RM − S − 1) Re cL Bo d
b
⎛ α PB
α TPB
1
0.76
⎜
= RM − S +
− 0.65 ⎜
1.17
0.6
−3
α REF
1 + 2.53 × 10 Re Bo (RM − S − 1)
⎝ α REF
⎞
⎟⎟
⎠
2
Kanały o średnicach konwencjonalnych
10000
4
R11+R12+R22
a=2.53*10^-3,b=1.17,c=0.6,d=-0.65
R11
R12
R22
3
αth/αexp
αth
R11+R12+R22
a=2.53*10^-3, b=1.17,c=0.6,d=-0.65
R11
R12
R22
y=x
+30%
-30%
1000
2
1
0
100
100
1000
αexp
10000
0.0
0.2
0.4
x
0.6
0.8
Ponad 63% obliczeń znajduje się w zakresie błędu ±30% dla przypadku
posiadanego banku danych
1.0
Kanały o małych średnicach
3
P=2.53*10^-3 Re^1.17 Bo^0.6 Co^-0.465
R11
R12
141b
134a
113
123
y=x
+30%
-30%
2
αth/αexp
αth
10000
P=2.53*10^-3 Re^1.17 Bo^0.6 Co^-0.465
R11
R12
141b
134a
113
123
1000
1
0
100
100
1000
αexp
10000
0.0
0.2
0.4
x
0.6
0.8
Ponad 64% obliczeń znajduje się w zakresie błędu ±30% dla przypadku
posiadanego banku danych dla kanałów o małych średnicach
1.0
Zasada działania rurki ciepła
kondensacja
sekcja adiabatyczna
parowanie
przepływ pary
ciepło
odprowadzone
knot
osłona
przepływ cieczy
ciepło
doprowadzone
Zasada działania rurki ciepła
szczelna obudowa
ciepło
odprowadzone
umowna granica podziałowa
ciepło
odprowadzone
powrót
kondensatu
para czynnika roboczego
ciepło
ciepło
doprowadzone
doprowadzone
wrzenie czynnika roboczego
Schemat działania rurki ciepła
Przykłady zastosowania rurek ciepła
rurowe
Zakrzywione rurowe
przegrodowe
pierścieniowe
Przykłady zastosowania rurek ciepła
Rurowe giętkie
Zmienny opór przewodzenia
Dioda
Upusty ciepła o dużej
pojemności
Ograniczenia zastosowań rurek ciepła
Lepkościowe – siły lepkości ograniczają przepływ pary w rdzeniu rurki ciepła
Dźwiękowe – przepływ pary osiąga prędkość dźwięku na wyjściu z części parownika
i powoduje stałą moc przy dużych gradientach temperatury,
Porywanie/zalewanie – para o dużym wydatku ogranicza spływ kondensatu do
parownika,
Kapilarne – suma grawitacyjnego, cieczowego i parowego ciśnienia przewyższa
kapilarne ciśnienie pompowania w strukturze knota,
Wrzenie – wrzenie błonowe w parowniku rurki ciepła z reguły zaczyna się przy
strumieniach ciepła 5-10 W/cm2 dla knotów odbijających oraz 25-35 W/cm2 dla
knotów z substancji porowatych.
Ograniczenia zastosowań rurek ciepła
Przykład
upustu
ciepła
1
2
3
Materiał
Diament
Srebro
Miedź
Aluminium
Całkowita
moc
W
25
90
4000
Liczba
rurek
ciepła
1
3
8
Moc na
jedną
rurkę
25
30
500
Powierzchnia
Długość
rurki
ΔT
cm2
0.28
0.32
2.85
U0
(na 1
rurkę)
cm
12.7
15.3
56.6
K
0.6
3.0
7.0
W/mK
189
48.5
142.4
2 000
410
386
180