WYMIANA CIEPŁA PRZY ZMIANACH STANU
SKUPIENIA
WYKŁAD 8
Dariusz Mikielewicz
Politechnika Gdańska
Wydział Mechaniczny
Katedra Techniki Cieplnej
Wymiana ciepła podczas wrzenia
Przejście fazy ciekłej w parową następuje, gdy faza ciekła jest przegrzana, tzn.
gdy jej temperatura jest wyższa od temperatury nasycenia. Powstawanie fazy
parowej związane jest z istnieniem zarodków będących źródłami tworzenia się
fazy, takich jak zanieczyszczenia w cieczy, rozpuszczone gazy, cząstki
promieniowania bądź fluktuacje gęstości lub nierówności na ściance.
Wymiana ciepła podczas wrzenia
Analiza wykazała, iż praca tworzenia się pęcherzyków parowych jest mniejsza dla
nierówności powierzchni jak dla zarodków istniejących w objętości cieczy, stąd też
faza parowa tworzy się z reguły na ściance, do której doprowadza się ciepło.
Zagadnienia wrzenia, podobnie jak zagadnienia konwekcji w jednej fazie dzielą się
w ogólności na zagadnienia, przy których geometria przestrzeni i hydrodynamika
przepływu nie wpływa istotnie na proces wymiany ciepła, nazywane wówczas
wrzeniem w objętości oraz na zagadnienia, w których kształt przestrzeni i
hydrodynamika przepływu faz ma zasadniczy wpływ na wymianę ciepła, nazywane
wrzeniem w przepływie.
Ponadto, przy małych strumieniach cieplnych, a zatem małych przegrzaniach cieczy
wrzenie ma charakter pęcherzykowy, zaś przy dużych strumieniach cieplnych, czyli
dużych przegrzaniach cieczy, zamiast pęcherzyków parowych na ściance tworzy się
błona parowa i takie wrzenie nazywa się wrzeniem błonowym.
Rozróżnia się także wrzenie przechłodzone, które ma miejsce gdy temperatura
cieczy w pewnej odległości od ścianki jest niższa od temperatury nasycenia i wrzenie
nasycone, gdy temperatura cieczy w całej rozpatrywanej objętości jest równa albo
nieco wyższa od temperatury nasycenia.
Wrzenie pęcherzykowe
Z warunku równowagi sił działających na pęcherzyk sferyczny, określonego
równaniem Laplace'a, wynika że różnica ciśnień między obu fazami jest
proporcjonalna do napięcia powierzchniowego
Δp = p v − p L =
pv
pL
σ
R
2σ
R
- ciśnienie fazy parowej,
- ciśnienie fazy ciekłej,
- napięcie powierzchniowe,
- promień pęcherzyka sferycznego,
Z powyższych zależności wynika, że temperatura nasycenia wewnątrz
pęcherzyka parowego TR,v będzie wyższa od temperatury nasycenia fazy ciekłej
lub temperatury nasycenia nad płaską powierzchnią Tv. Poszukiwane
przegrzanie będzie więc wynosić ΔT = TR,v-Tv
Nasycone wrzenie w objętości
para
ciecz
pęcherze
parowe
Ciało stałe
z
Wrzenie przechłodzone: Tl<Tsat
z
Wrzenie nasycone: Tl>Tsat
Doświadczenie Nukiyamy
Para wodna, p=1 atm
Woda, Ts
drucik platynowy, q, ΔTe=Tw-Ts
Stanowisko Nukiyamy do pokazania procesu wrzenia
w objętości kontrolując strumień ciepła
Wizualizacja wrzenia w doświadczeniu Nukiyamy
Powstawanie pęcherzyków parowych
(a) obszar pojedynczych pęcherzyków
(b) obszar korków i kolumn (strugi parowe)
(c) Obszar wrzenia błonowego
Wyidealizowane strugi
parowe
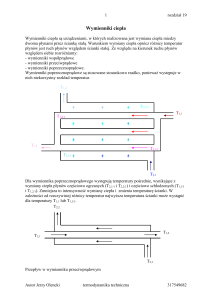
Krzywa wrzenia– Nukiyama (1934)
Kontrolowany strumień ciepła
Kontrolowana temperatura
powierzchni
AB – Konwekcja jednofazowa
BC – Wrzenie pęcherzykowe
CF – Wrzenie przejściowe
FDE – Rozwinięte wrzenie błonowe
α
Krzywa wrzenia
Początek wrzenia (tzw. zerowy
kryzys wrzenia): przejście z 1F w
2F wrzenie pęcherzykowe
q
parowanie
q
wrzenie
kr
kr
-1
wrzenie blonowe
pęcherzykowe
P
K1
1
q
10
q
P
2
10
0
10
Kryzys wrzenia pierwszego
rodzaju: przejście wrzenia
pęcherzykowego w przepływ
błonowy
K2
2
1
10
2
1
Kryzys wrzenia drugiego rodzaju: odejście
od struktury błonowej i powrót do wrzenia
pęcherzykowego
Punkt Leidenfrosta
10
3
10 4
ΔT
Correlations for pool boiling (αPB)
Cooper (1984)
0.12−0.4343ln Rp
αPB = 55pr
(− 0.434ln pr )−0.55M −0.5(qw)0.67
uogólniony model Cooper’a
α PB = AAp
0.12
r
(− ln pr )
−0.55
M
−0.5
(qw)
2/3
(19)
(18)
Gorenflo(1989)
α PB
⎡ qw ⎤
= α o FPF ⎢ ⎥
⎣ q0 ⎦
nf
⎡ Rp ⎤
⎢
⎥
R
⎢⎣ po ⎥⎦
0.133
F PF = 1 .2 p r0.27 + 2 .5 p r +
nf = 0 . 9 − 0 . 3 p r0 .3
(20)
pr
1 − p r (21)
(22)
Przepływ dwufazowy nieadiabatyczny
Podczas przepływu:
¾ zmienia się masowa zawartość
fazy parowej x wzdłuż kanału,
wymiana ciepła
przez konwekcję
.
.
.
¾ zmienia się stopień zapełnienia
kanału,
¾ zmienia się lokalny współczynnik
przejmowania ciepła przy ściance.
.
wrzenie
Przepływ fazy parowej
.
.
.
.
.
.
.
. .
.
.
. . .
.
.
.
. .
.
.
.
.
.
.
. .
. .
.
rozwinięte
przepływ mgłowy (ciecz
w postaci mgły w parze)
Przepływ pierścieniowy
(para z zawieszonymi kropelkami
cieczy wypełnia środek rury; cienka
warstwa cieczy na ściankach)
Przepływ korkowy
(duże pęcherze pary)
kierunek
doprowadzania ciepła
(promieniowy wzdłuż
długości kanału
Przepływ cieczy
o temperaturze nasycenia
( brak kondensacji
pęcherzyków pary )
wrzenie przechłodzone
Przepływ cieczy niedogrzanej
o temperaturze nasycenia przy
ściance (brak pęcherzyków pary)
wymiana ciepła
przez konwekcję
Przepływ cieczy niedogrzanej
do temperatury nasycenia
(brak pęcherzyków pary)
kierunek przepływu
Struktury przepływu dwufazowego
pęcherzykowy
mgłowy
korkowy
pierścieniowy
Struktury przepływu dwufazowego, q=var
duża wartość
strumienia cieplnego
średnia wartość
strumienia cieplnego
mała wartość
strumienia
cieplnego
Kryzys wrzenia w przepływie
DNB (PWR)
Dryout (CANDU)
Początek wrzenia nasyconego
woda
Alkyl (8-16) C=300ppm
qw=90 kW/m2
m& = 5.7 kg / m 2 s
Rozwinięte wrzenie nasycone
woda
qw=90 kW/m2
m& = 5.7 kg / m s
2
Alkyl (8-16) C=300ppm
Kryzys wrzenia I rodzaju - dryout
woda
qw=90 kW/m2
m& = 5.7 kg / m s
2
Alkyl (8-16) C=300ppm
Korelacje empiryczne
Korelacje oparte na parametrze Martinellego Xtt
α
= a( X
α
⎛ 1− x⎞
X tt = ⎜
⎟
⎝ x ⎠
tt
)
⎛ ρv ⎞
⎜ ⎟
⎝ ρl ⎠
0.5
⎛ μl ⎞
⎜ ⎟
⎝ μv ⎠
0.1
Dengler & Addoms: a=3.5 i b=-0.5,
b
tp
0.9
Guerrieri & Talty
a=3.4 i b=-0.45
l
α
= a ' [Bo + m( X
α
) ] Collier & Pulling:
b
tp
tt
Schrock & Grossman: a'=7400, b=0.66 & m = 0.00015
l
⎛α ⎞
α
⎟⎟
= 1 + ⎜⎜
α
⎝α ⎠
TPb
Pb
l
l
2
Kutateladze
a'=6700, b=0.66 & m = 0.00035
Istniejące metody
α TPB = S α Pb + F α cb
1.
Uogólnienie małej liczby indywidualnych danych eksperymentalnych
autorów w małym zakresie zmian parametrów
2.
Uogólnienie dużej liczby danych z wielu źródeł danych w dużym zakresie
zmian parametrów
Żadna ze znanych korelacji nie ma podstaw teoretycznych!
Modyfikacja korelacji - 2006
RM − S
α
f =
α
GO
1z
LO
⎡
⎞ ⎤
⎛1
1
= ⎢1 + 2⎜⎜ − 1⎟⎟ x ⎥ ⋅ (1 − x)1 / 3 + x 3
f 1z
⎢⎣
⎠ ⎥⎦
⎝ f1
μ c ⎛λ ⎞
⎜ ⎟
=
μ c ⎜⎝ λ ⎟⎠
G
pL
L
L
pG
G
α TPB
1 ⎛ α PB
0.76
⎜⎜
= RM − S +
α REF
1 + p ⎝ α REF
⎛ dp ⎞
⎜⎜ ⎟⎟
dp ⎠
⎝
f =
⎛ dp ⎞
⎜ ⎟
⎝ dz ⎠
3/ 2
GO
1
⎞
⎟⎟
⎠
2
⎛μ
= ⎜⎜
⎝μ
L
G
⎞
⎟
⎟
⎠
1/ 4
ρ
ρ
G
L
LO
P = a(RM − S − 1) Re cL Bo d
b
⎛ α PB
α TPB
1
0.76
⎜
= RM − S +
− 0.65 ⎜
−3
1.17
0.6
α REF
1 + 2.53 × 10 Re Bo (RM − S − 1)
⎝ α REF
⎞
⎟⎟
⎠
2