Obwody magnetyczne sprzężone

Obwody magnetyczne sprzęŜone ... 1/23
OBWODY MAGNETYCZNE SPRZĘśONE
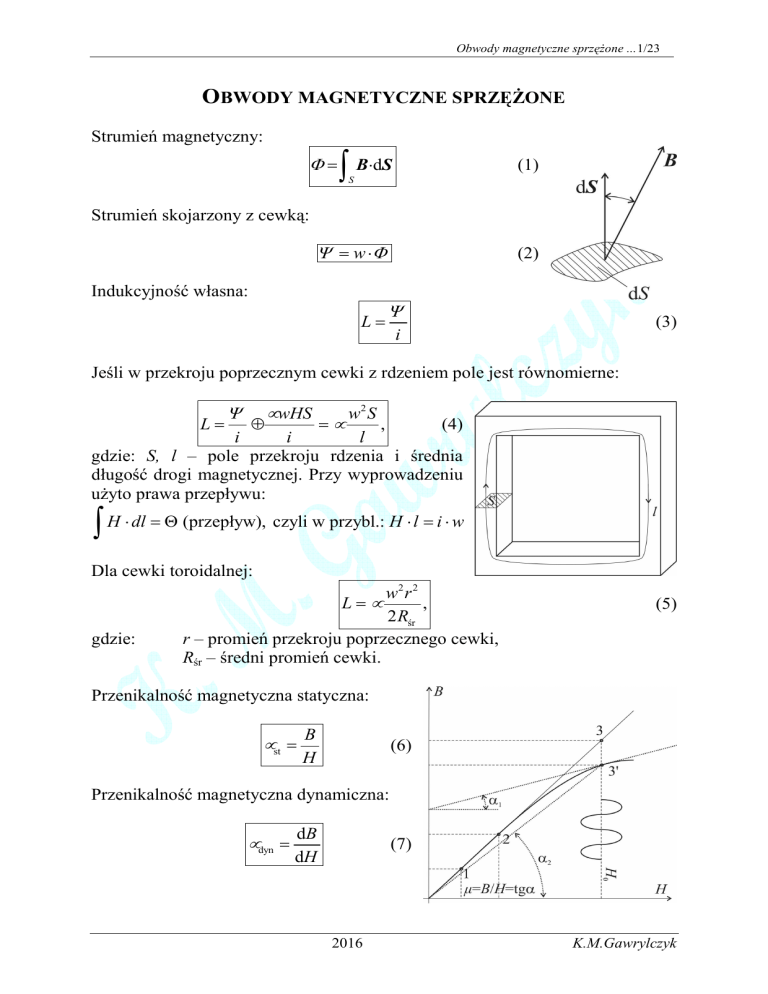
Strumień magnetyczny:
∫
Φ = B⋅dS
(1)
S
Strumień skojarzony z cewką:
Ψ = w ⋅Φ
Indukcyjność własna:
L=
(2)
Ψ
(3)
i
Jeśli w przekroju poprzecznym cewki z rdzeniem pole jest równomierne:
Ψ
µ wHS
w2 S
,
(4)
i
i
l
gdzie: S, l – pole przekroju rdzenia i średnia
długość drogi magnetycznej. Przy wyprowadzeniu
uŜyto prawa przepływu:
L=
≈
=µ
∫ H ⋅ dl = Θ (przepływ), czyli w przybl.: H ⋅ l = i ⋅ w
Dla cewki toroidalnej:
w2 r 2
,
2 Rśr
r – promień przekroju poprzecznego cewki,
Rśr – średni promień cewki.
L=µ
gdzie:
(5)
Przenikalność magnetyczna statyczna:
µst =
B
H
(6)
Przenikalność magnetyczna dynamiczna:
µdyn =
dB
dH
(7)
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 2/23
INDUKCYJNOŚĆ WZAJEMNA
Rys. 1. Podział całkowitego strumienia na strumień główny i rozproszenia.
Strumień główny i strumień rozproszenia:
Φ11 = Φ1g +Φ1s
(8)
Strumienie magnetyczne skojarzone z cewką 1 oraz cewką 2 wynoszą:
Ψ11 = w1Φ11 , Ψ1g = w1Φ1g , Ψ1s = w1Φ1s ,
Ψ12 = w2Φ1g
(9)
Indukcyjność własna cewki 1:
L1 =
Ψ11
i1
=
w1Φ11
i1
(10)
Indukcyjność wzajemna cewki 1 z cewką 2:
M 12 =
Ψ12
2016
i1
=
w2Φ1g
i1
(11)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 3/23
Po przełączeniu zasilania do cewki 2 będzie:
Φ22 = Φ2 g +Φ2 s
(12)
Indukcyjność własna cewki 2:
L2 =
Ψ 22
i2
=
w2Φ22
i2
(13)
Indukcyjność wzajemna cewki 2 z cewką 1:
M 21 =
Ψ 21
i2
=
w1Φ2g
(14)
i2
Jeśli cewki znajdują się w środowisku o takiej samej przenikalności
magnetycznej µ, to indukcyjności wzajemne są takie same:
M 12 = M 21 = M =
2016
Ψ12 Ψ 21
i1
=
i2
(15)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 4/23
INDUKCYJNOŚĆ GŁÓWNA I INDUKCYJNOŚĆ ROZPROSZENIA
Indukcyjność główna cewki 1 oraz cewki 2:
L1g =
Ψ1g
i1
=
w1Φ1g
i1
, L2g =
Ψ 2g
i2
=
w2Φ2g
(16)
i2
Indukcyjność rozproszenia cewki 1 oraz cewki 2:
L1s =
Ψ1s
i1
=
w1Φ1s
Ψ
wΦ
, L2s = 2s = 2 2s
i1
i2
i2
(17)
Ze względu na wzór (8) otrzymuje się:
L1 = L1g + L1s , L2 = L2g + L2s
(18)
ZaleŜność pomiędzy indukcyjnościami głównymi a indukcyjnością wzajemną:
L1g w12
w2
w1
L1g = M =
L2g , czyli:
, oraz: M = L1g L2g
=
w1
w2
L2g w22
(19)
Indukcyjność wzajemna jest średnią geometryczną indukcyjności
głównych.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 5/23
WSPÓŁCZYNNIK SPRZĘśENIA
Φ1g Φ1s
+
=1
Φ11 Φ11
(20)
Współczynniki sprzęŜenia cewek 1 i 2:
k1 =
Φ1g
Φ
, k2 = 2g
Φ11
Φ22
(21)
Współczynniki rozproszenia cewek 1 i 2:
σ1 =
Ich suma:
Φ1s
Φ
, σ 2 = 2s
Φ11
Φ22
(22)
k1 + σ 1 = 1, k2 + σ 2 = 1
(23)
k1k2 = 1 − (σ 1 + σ 2 − σ 1σ 2 )
(24)
Iloczyn:
Współczynnikiem sprzęŜenia cewek nazywamy średnią geometryczną:
k = k1k2
(25)
Wypadkowy współczynnik rozproszenia to dopełnienie wzoru (24) do jedynki:
σ = σ 1 + σ 2 − σ 1σ 2
(26)
k2 +σ =1
(27)
Wtedy:
Współczynniki sprzęŜenia moŜna wyliczyć z proporcji:
k1 =
L1g
L1
, k2 =
L2g
L2
, 0 ≤ k ≤ 1.
(28)
a po uwzględnieniu równania (19)
M = k L1 L2
2016
(29)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 6/23
ZWROT NAWINIĘCIA CEWEK A ZNAK INDUKCYJNOŚCI WZAJEMNEJ
Rys. 2. Dwie cewki sprzęŜone o zgodnym i przeciwnym kierunku nawinięcia.
Gwiazdka oznacza początek uzwojenia. JeŜeli przy połączeniu 1 i 2 strumienie
się dodają (prądy w cewkach są wtedy zgodne), znak indukcyjności wzajemnej
jest +M.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 7/23
BILANS NAPIĘĆ PRZY ZGODNYM NAWINIĘCIU CEWEK
Rys. 3. Cewki nawinięte zgodnie i ich schemat.
Bilans napięć strony pierwotnej przy i2 = 0:
R1i1 + L1
di1
= u1
dt
(30)
Po pojawieniu się prądu i2 zgodnie z prawem Faraday'a strumień z nim
związany indukuje po stronie pierwotnej siłę elektromotoryczną e1, podobnie dla
strony wtórnej:
e1 = −
∂Ψ 21
∂i
∂Ψ
∂i
= − M 2 , e2 = − 12 = − M 1
∂t
∂t
∂t
∂t
(31)
Bilans napięć dla obydwu stron:
∂i1
∂i
+ M 2 = u1
∂t
∂t
∂i
∂i
R2i2 + L2 2 + M 1 = −u2
∂t
∂t
R1i1 + L1
2016
(32)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 8/23
BILANS NAPIĘĆ PRZY PRZECIWNYM NAWINIĘCIU CEWEK
Rys. 4. Cewki nawinięte przeciwnie i ich schemat.
Bilans napięć strony pierwotnej przy i2 = 0:
R1i1 + L1
di1
= u1
dt
(33)
Po pojawieniu się prądu i2 zgodnie z prawem Faraday'a strumień z nim
związany indukuje po stronie pierwotnej siłę elektromotoryczną e1, podobnie dla
strony wtórnej (indukcyjność wzajemna jest ujemna):
e1 = −
∂Ψ 21
∂i
∂Ψ
∂i
= M 2 , e2 = − 12 = M 1
∂t
∂t
∂t
∂t
(34)
Bilans napięć dla obydwu stron:
∂i1
∂i
− M 2 = u1
∂t
∂t
∂i
∂i
R2i2 + L2 2 − M 1 = −u2
∂t
∂t
R1i1 + L1
2016
(35)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 9/23
POŁĄCZENIE SZEREGOWE CEWEK SPRZĘśONYCH
Rys. 5. Połączenie szeregowe cewek nawiniętych zgodnie i przeciwnie.
Strumienie skojarzone przy zgodnym kierunku nawinięcia cewek:
Ψ1 = Ψ11 +Ψ 21 = ( L1 + M ) i
Ψ 2 = Ψ 22 +Ψ12 = ( L2 + M ) i
(36)
Indukcyjność całego połączenia:
L=
Ψ
i
=
Ψ1 +Ψ 2
i
= L1 + L2 + 2 M
(37)
Strumienie skojarzone przy przeciwnym nawinięciu cewek:
Ψ1 = Ψ11 −Ψ 21 = ( L1 − M ) i
Ψ 2 = Ψ 22 −Ψ12 = ( L2 − M ) i
(38)
Indukcyjność całego połączenia:
L=
Ψ
i
=
Ψ1 +Ψ 2
i
2016
= L1 + L2 − 2 M
(39)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 10/23
Gdy współczynnik sprzęŜenia między cewkami wynosi k = 1, wtedy:
L = L1 + L2 ± 2 M = L1 + L2 ± 2 L1L2 =
(
L1 ± L2
)
2
(40)
Inny przypadek szczególny, to cewki jednakowe:
L1 = L2 , wtedy przy zgodnym nawinięciu L = 4 L, przy przeciwnym L = 0.
(41)
Gdy współczynnik sprzęŜenia wynosi k = 0, to:
L = L1 + L2 niezaleŜnie od kierunku nawinięcia cewek.
(42)
Wprowadzając współczynnik sprzęŜenia k moŜna udowodnić, Ŝe wypadkowa
indukcyjność jest zawsze dodatnia:
L = L1 + L2 − 2 M = L1 + L2 − 2k L1 L2 ≥ L1 + L2 − 2 L1 L2 =
2016
(
L1 − L2
) ≥0
2
(43)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 11/23
POŁĄCZENIE RÓWNOLEGŁE CEWEK SPRZĘśONYCH
Rys. 6. Połączenie równoległe cewek nawiniętych zgodnie i przeciwnie.
Impedancje zespolone cewek, bez sprzęŜenia:
Z1 = R1 + jω L1 , Z 2 = R2 + jω L2
(44)
Impedancja związana ze sprzęŜeniem:
Z12 = Z 21 = jω M
(45)
Bilans napięć przy zgodnym nawinięciu:
Z1 I 1 + Z 21 I 2 = U
Z12 I 1 + Z 2 I 2 = U
Stąd prądy w cewkach wynoszą:
Z − Z12
Z − Z12
I1 = 2
U, I 2 = 1
U
2
Z1Z 2 − Z12
Z1Z 2 − Z122
(46)
(47)
Impedancja wejściowa układu cewek zgodnie nawiniętych:
Z=
U
U
Z1Z 2 − Z122
=
=
I I 1 + I 2 Z1 + Z 2 − 2 Z12
2016
(48)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 12/23
Bilans napięć przy przeciwnym kierunku nawinięcia:
Z1 I 1 − Z 21 I 2 = U
(49)
− Z12 I 1 + Z 2 I 2 = U
Impedancja wejściowa wynosi wtedy:
Z1Z 2 − Z122
Z=
Z1 + Z 2 + 2 Z12
(50)
Gdy nie ma sprzęŜeń: M = 0, Z12 = jωM = 0
Z=
Z1Z 2
Z1 + Z 2
(51)
Gdy rezystancje są równe zeru, Z1 = jωL1, Z2 = jωL2 i dla zgodnego i
przeciwnego kierunku nawinięcia cewek otrzymuje się:
L1 L2 − M 2
L=
L1 + L2 ∓ 2 M
a) cewki nawinięte zgodnie:
(52)
b) cewki nawinięte przeciwnie:
Rys. 6a. Indukcyjność zastępcza połączenia równoległego dwóch jednakowych
cewek o indukcyjności 1mH w funkcji współczynnika sprzęŜenia k.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 13/23
TRANSFORMATOR POWIETRZNY
Rys. 7. Transformator powietrzny o cewkach nawiniętych przeciwnie.
Bilans napięć transformatora przy przeciwnym kierunku nawinięcia cewek:
R1 I 1 + jω L1 I 1 − jω MI 2 = U1
R2 I 2 + jω L2 I 2 − jω MI 1 = − Z obc I 2 = −U 2
(53)
Wykres wskazowy odpowiadający schematowi z rys. 7:
R1 I 1 + jω L1 I 1 − jω MI 2 = U1
R2 I 2 + jω L2 I 2 + Robc I 2 + jX obc I 2 = jω MI 1
Rys. 8. Wykres wskazowy.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 14/23
Rys. 9. Transformator powietrzny o cewkach nawiniętych zgodnie.
Bilans napięć transformatora przy zgodnym kierunku nawinięcia cewek:
R1 I 1 + jω L1 I 1 + jω MI 2 = U1
R2 I 2 + jω L2 I 2 + jω MI 1 = − Z obc I 2 = −U 2
(54)
Wykres wskazowy odpowiadający schematowi z rys. 9 zgodnie z równaniem
(54) o postaci:
R1 I 1 + jω L1 I 1 + jω MI 2 = U1
R2 I 2 + jω L2 I 2 + Robc I 2 +jX obc I 2 = − jω MI 1
Rys. 10. Wykres wskazowy.
Na obu ostatnich wykresach wskazowych przyjęto, Ŝe odbiornik ma charakter
indukcyjno-czynny:
Z obc = Robc + jX obc
2016
(55)
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 15/23
SCHEMAT ZASTĘPCZY TRANSFORMATORA POWIETRZNEGO
Układ równań (53) moŜna zapisać w postaci macierzowej:
 R1 + jω L1
 − jω M

− jω M   I 1   U 1 
=
R2 + jω L2   I 2   −U 2 
(56)
Układ ten opisuje następujący schemat zastępczy:
Rys. 11. Schemat zastępczy transformatora z cewkami nawiniętymi przeciwnie.
Bilans napięć schematu zastępczego (metoda oczkowa) daje to samo równanie
(56):
I 1 [ R1 + jω ( L1 − M ) + jω M ] − I 2 jω M = U1
− I 1 jω M + I 2 [ R2 + jω ( L2 − M ) + jω M ] = −U 2
Natomiast układowi (54) moŜna nadać postać:
 R1 + jω L1
 − jω M

− j ω M   I 1  U 1 
=
R2 + jω L2   − I 2  U 2 
(57)
któremu odpowiada układ zastępczy (bilans napięć jest analogiczny, jak
powyŜej, wystarczy zmienić znak I2 oraz U2):
Rys. 12. Schemat zastępczy transformatora z cewkami nawiniętymi zgodnie.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 16/23
CEWKA NA RDZENIU STALOWYM
Napięcie jest związane ze strumieniem magnetycznym przez prawo Faraday'a:
e=−
dΨ
dΦ
= −w
dt
dt
(58)
Dla przebiegu sinusoidalnego moŜna podać wzór:
E=
Em 2 π
=
⋅ f ⋅ w ⋅Φm = 4, 44 ⋅ f ⋅ w ⋅Φm = 4, 44 ⋅ f ⋅ w ⋅ Β m ⋅ S rdz
2
2
(59)
Prąd jest związany z natęŜeniem pola magnetycznego przez prawo przepływu:
w ⋅ I = H ⋅ l , gdzie: l − średnia długość drogi magnetycznej w rdzeniu. (60)
Rys. 13. Przebiegi prądu i napięcia na cewce z rdzeniem stalowym, wymuszone napięcie.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 17/23
Przy wymuszonym napięciu w cewce powstają wysokie impulsy prądu.
Natomiast przy zasilaniu cewki wymuszonym prądem sinusoidalnym ma
miejsce odwrotna sytuacja, następuje spłaszczenie krzywej napięcia na cewce
będące wynikiem nasycenia rdzenia:
Rys. 14. Przebiegi prądu i napięcia na cewce z rdzeniem stalowym, wymuszony prąd.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 18/23
PĘTLA HISTEREZY, STRATY ZWIĄZANE Z HISTEREZĄ
Rys. 15. Pętla histerezy materiału ferromagnetycznego.
Straty na histerezę są związane z energią przemagnesowania materiału po
∫
krzywej histerezy W = BdH . Ich wartość podają wzory Richtera:
f
2
Bm
(61)
100
Prądy wirowe w materiale przewodzącym są związane z istnieniem zmiennego
pola magnetycznego:
∂B
rotE = − , gęstość prądu J = γ E .
(62)
∂t
Drugi wzór Richtera podaje wartość strat na prądy wirowe:
2
2
 f 
pw = σ 
(63)
 Bm
 100 
ph = ε
Współczynniki Richtera dla róŜnych blach:
Zawartość krzemu [%]
0,5
1
2,5
Grubość blachy
1,0
0,5
0,5
0,5
0,5
CięŜar wł. blachy
7,85 7,85
7,8
7,7
7,6
4,4
4,4
4,2
3,8
2,8
Współczynnik ε
22,4
5,6
2,6
1,6
1,1
Współczynnik σ
Stratność p10
7,8
3,6
2,8
2,3
1,7
2016
4,0
0,35mm
7,6G/cm3
2,1
1,1
1,3W/kg
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 19/23
SCHEMAT ZASTĘPCZY CEWKI NA RDZENIU STALOWYM
Rys. 16. Schemat zastępczy cewki z rdzeniem oraz wykres wskazowy napięć i prądów.
Wielkości występujące na schemacie zastępczym:
U, I
E
RCu
RFe
Ls
Lµ
- napięcie i prąd zasilający (symboliczne),
- siła elektromotoryczna indukowana przez strumień Φ,
- rezystancja uzwojeń cewki,
- rezystancja zastępująca straty w rdzeniu stalowym,
- indukcyjność rozproszenia cewki,
- indukcyjność główna (magnesująca) cewki.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 20/23
TRANSFORMATOR.
SPROWADZENIE WIELKOŚCI WTÓRNYCH NA STRONĘ PIERWOTNĄ
Rys. 17. Sprowadzenie wielkości wtórnych na stronę pierwotną przy zgodnym nawinięciu
uzwojeń.
Przy n = w1/w2 wielkości sprowadzone do strony pierwotnej wynoszą:
i2' = i2/n,
u2' = n·u2,
R2' = n2·R2,
L2s' = n2·L2s,
Z2' = n2·Z2
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 21/23
Rys. 18. Schemat zastępczy transformatora z uzwojeniami nawiniętymi zgodnie.
Rys. 19. Wykres wskazowy dla transformatora z uzwojeniami nawiniętymi zgodnie
przy obciąŜeniu indukcyjno-czynnym:
U2
= Z obc = Robc + jX obc .
I2
Wielkości strony wtórnej pokazano na wykresie przed przeliczeniem na stronę
pierwotną.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 22/23
Rys. 20. Schemat zastępczy transformatora z uzwojeniami nawiniętymi przeciwnie.
Rys. 21. Wykres wskazowy dla transformatora z uzwojeniami nawiniętymi przeciwnie
U 2'
'
'
'
przy obciąŜeniu indukcyjno-czynnym: ' = Z obc = Robc + jX obc .
I2
Na tym wykresie przedstawiono jedynie wielkości strony wtórnej sprowadzone
do pierwotnej.
2016
K.M.Gawrylczyk
Obwody magnetyczne sprzęŜone ... 23/23
TRANSFORMATOR IDEALNY. AUTOTRANSFORMATOR
Transformator idealny charakteryzuje się brakiem strat w uzwojeniach, jak teŜ
w rdzeniu. Indukcyjność główna jest nieskończenie wielka, co powoduje, Ŝe
prąd magnesujący jest równy zeru. W zaleŜności od kierunku nawinięcia
uzwojeń charakteryzują go równania:
 U1   ∓ n 0   U 2 

=


(64)
1
I1   0 ∓ I 2 

 

n  
Impedancja dołączona na jego wyjście jest przetwarzana przez n2, co jest
własnością typową dla konwerterów:
Z we = n 2 Z obc
(65)
Autotransformator
Dla uproszczenia rozwaŜań autotransformator zostanie przedstawiony bez
uwzględnienia strat w rdzeniu i w miedzi, jak teŜ z pominięciem indukcyjności
rozproszenia.
Rys. 22. Schemat autotransformatora.
Autotransformator jest transformatorem jednouzwojeniowym. Z bilansu prądów
łatwo wyprowadzić, Ŝe:
I 3 = I1 + I 2 = I1 −
w1
w − w2
I1 = −I1 1
, czyli przy w1 = w2 ⇒ I 3 = 0.
w2
w2
2016
(66)
K.M.Gawrylczyk