mje-2008-matematyka-2G-e2

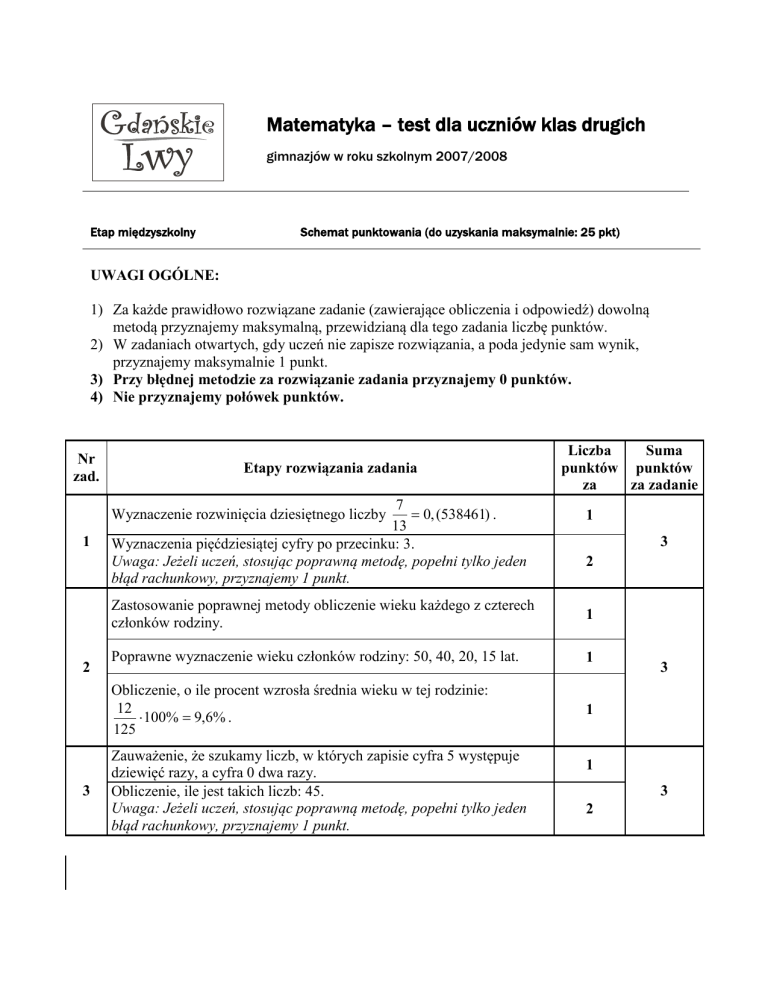
Matematyka – test dla uczniów klas drugich
gimnazjów w roku szkolnym 2007/2008
Etap międzyszkolny
Schemat punktowania (do uzyskania maksymalnie: 25 pkt)
UWAGI OGÓLNE:
1) Za każde prawidłowo rozwiązane zadanie (zawierające obliczenia i odpowiedź) dowolną
metodą przyznajemy maksymalną, przewidzianą dla tego zadania liczbę punktów.
2) W zadaniach otwartych, gdy uczeń nie zapisze rozwiązania, a poda jedynie sam wynik,
przyznajemy maksymalnie 1 punkt.
3) Przy błędnej metodzie za rozwiązanie zadania przyznajemy 0 punktów.
4) Nie przyznajemy połówek punktów.
Nr
zad.
Etapy rozwiązania zadania
7
 0, (538461) .
13
Wyznaczenia pięćdziesiątej cyfry po przecinku: 3.
Uwaga: Jeżeli uczeń, stosując poprawną metodę, popełni tylko jeden
błąd rachunkowy, przyznajemy 1 punkt.
Wyznaczenie rozwinięcia dziesiętnego liczby
1
2
3
Liczba
Suma
punktów punktów
za
za zadanie
1
3
2
Zastosowanie poprawnej metody obliczenie wieku każdego z czterech
członków rodziny.
1
Poprawne wyznaczenie wieku członków rodziny: 50, 40, 20, 15 lat.
1
Obliczenie, o ile procent wzrosła średnia wieku w tej rodzinie:
12
 100%  9,6% .
125
1
Zauważenie, że szukamy liczb, w których zapisie cyfra 5 występuje
dziewięć razy, a cyfra 0 dwa razy.
Obliczenie, ile jest takich liczb: 45.
Uwaga: Jeżeli uczeń, stosując poprawną metodę, popełni tylko jeden
błąd rachunkowy, przyznajemy 1 punkt.
3
1
3
2
4
5
6
7
Zauważenie, że aby dany trójkąt był równoramienny konieczne jest by
prawdziwe było jedno z równań:
2m  2  m  8  2m  2  3m  1  m  8  3m  1 .
Wyznaczenie wartości parametru m, które spełniają równania:
m  6  m  1  m  3,5 .
Sprawdzenie, dla wyznaczonych wartości parametru, czy dane długości
odcinków spełniają nierówność trójkąta.
Podanie odpowiedzi: m  6  m  3,5 .
Dorysowanie promieni do końców cięciwy i zaznaczenie kąta między
dorysowanymi promieniami.
1
Zauważenie, że pole zacieniowanego obszaru jest równe różnicy pola
3
koła o promieniu 8 i trójkąta równobocznego o boku 8.
Poprawna metoda wyznaczenia pól wycinka koła i trójkąta.
4
Poprawne obliczenia i podanie odpowiedzi: P  16(   3 ) .
3
Poprawne wykonanie rysunku pomocniczego.
Wyznaczenie pola każdej z trzech części: 48 cm².
Zapisanie warunku pozwalającego wyznaczyć szukaną odległość: np.
1 2
x  48, gdzie x oznacza długość przyprostokątnych trójkątów
2
odciętych z kwadratu przez proste równoległe.
1
1
4
1
1
1
1
4
1
1
1
1
1
Rozwiązanie zapisanego warunku: x  4 6 .
1
Wyznaczenie szukanej odległości: (6 2  4 3 ) cm .
Zastosowanie własności potęg do uzasadnienia danej nierówności.
Przeprowadzenie poprawnego rozumowania pozwalającego uzasadnić
daną nierówność.
1
1
2
5
3