i. logiczne struktury drzewiaste

I. LOGICZNE STRUKTURY DRZEWIASTE
Analizując dany problem uzyskuje się zadanie projektowe w postaci pewnego zbioru
danych. Metoda morfologiczna, która została opracowana w latach 1938-1948 przez
amerykańskiego astrofizyka F. Zwicky’ego [1] polega na analizie wszystkich rozwiązań
danego problemu. Najlepsze rozwiązania wybierane są z uporządkowanego zapisu możliwych
rozwiązań (danych).
Logiczne struktury drzewiaste pozwalają uzyskać uporządkowany zapis rozwiązań
danego zadania projektowego. Możliwe rozwiązanie danego zadania oznacza ścieżkę na
drzewie logicznym (od korzenia na dole do wierzchołka na górze), a zbiór wszystkich
ścieżek jest zbiorem wszystkich możliwych rozwiązań. Każda gałązka jest elementarną
decyzją, czyli pojedynczym literałem. W szczególności, taka interpretacja może być
przeprowadzona z wykorzystaniem dwu- i wielowartościowych tablic decyzyjnych [2, 3]
I. 1 Drzewo logiczne
Drzewo logiczne jest logiczną strukturą drzewiastą, w której wartości logiczne
zmiennych są kodowane na gałązkach drzewa. Na danym poziomie drzewa może występować
tylko jedna zmienna logiczna, przy czym liczba pięter jest dokładnie równa liczbie zmiennych
niezależnych danej funkcji logicznej [3]. Przedstawienie danej funkcji boolowskiej, zapisanej
w kanonicznej alternatywnej postaci normalnej (KAPN), na drzewie logicznym polega na
zakodowaniu poszczególnych iloczynów kanonicznych na ścieżce drzewa od korzenia do
wierzchołka końcowego [4].
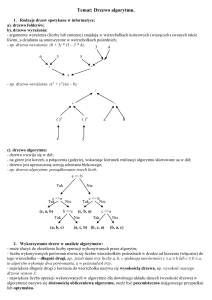
Przykł. 1.1
Na rys. 1.1 przedstawiono drzewo logiczne na którym zakodowano funkcję boolowską
trzech zmiennych. Pogrubione ścieżki od korzenia do wierzchołków końcowych są
zakodowaniem odpowiednich iloczynów kanonicznych danej funkcji i oznaczają rozwiązania
realizowalne.
f ( x1 , x2 , x3 )  x1 x2 x3  x1 x2 x3 
x1 x2 x3  x1 x2 x3
Rys. 1.1 Funkcja boolowska trzech zmiennych zakodowana na drzewie logicznym
Algorytm Quine’a –Mc Cluskeya pozwala upraszczać funkcje boolowskie zapisane w KAPN,
otrzymując skrócona alternatywną postać normalną (SAPN), a następnie minimalną
alternatywną postać normalną (MAPN) [4]. Uzyskuje się wówczas zminimalizowaną postać
wyjściowej funkcji w sensie liczby literałów- Dlatego mówimy o skreśleniach pełnych
wiązek gałązek prawdziwych (OD GÓRY DO DOŁU!!) jako uproszczenia graficzne
umożliwiające uzyskiwanie minimalnych postaci decyzyjnych.
Przykł. 1.2
Na rys. 1.2 przedstawiono drzewo logiczne z zaznaczonymi wszystkimi możliwymi
uproszczeniami graficznymi oraz uproszczone drzewo logiczne (realizowalne rozwiązania
pewnego zadania oraz podrozwiązania danego zadania).
Rys. 1.2 Drzewo logiczne i uproszczone drzewo logiczne
I. 2. Optymalne drzewo logiczne
Optymalnym drzewem logicznym nazywa się takie tradycyjne drzewo logiczne, które
po uproszczeniu ma minimalną liczbę gałązek przy braku gałązek izolowanych i stanowi
wytyczne dla decydenta w sensie rangi ważności parametrów decyzyjnych. Oznacza to, że
nawet mała zmiana wartości liczbowej arytmetycznej ważnego parametru może spowodować
radykalną zmianę (dobrą lub złą) w zachowaniu się badanego układu obiektu, natomiast
nawet duże zmiany wartości liczbowych mało ważnych parametrów nie powodują dużych
zmian w zachowaniu się badanego układu [4, 5].
W przypadku istnienia kilku drzew z najmniejszą liczbą gałęzi prawdziwych
należy takie drzewa traktować równoprawnie.
Przykł. 2.1
Dla funkcji logicznej zapisanej kodowo w KAPN w Tab. 2.1, zbudowano drzewo
logiczne, które po uproszczeniu graficznym ma 11 gałązek (Rys. 2.1) i drzewa logiczne, które
po uproszczeniu graficznym mają 10 gałązek (Rys. 2.2).
Tab. 2.1 Kodowy zapis funkcji boolowskiej
x1
x2
x3
1
0
1
0
2
1
0
0
3
0
0
2
4
0
1
1
5
1
1
0
6
0
1
2
7
1
1
2
Rys. 2.1 Nieoptymalne drzewo logiczne
Rys. 2.2 Optymalne drzewa logiczne
[1] ZWICKY F.; Discovery, Invention; Research Trough the Morphological Analysis;
Macmil, 1969 Toronto
[2] PARTYKA M. A.; Design methodology –some selected problems of engineering design,
Skrypt nr 241, Polit. Opol., Opole 2001
[3] PARTYKA M. A.; Logika wielowartościowych procesów decyzyjnych; Wydawnictwo
Naukowo-Techniczne, Warszawa 2002
[4] PARTYKA M. A.; Algorytm Quine’a Mc Cluskeya minimalizacji indywidualnych
cząstkowych wielowartościowych funkcji logicznych; St. i Monog. z.109, Polit. Opol., Opole
1999
[5] DEPTUŁA A.: Analiza porównawcza optymalnych zmodyfikowanych drzew
logicznych w ocenie odporności parametrów układu na zmiany warunków pracy;
XXXVIII Konf. Zast. Mat., Zakopane 2009, Inst. Mat. PAN, Warszawa 2009.
.
.
.
.