termodynamika_cz._vii_new_druk

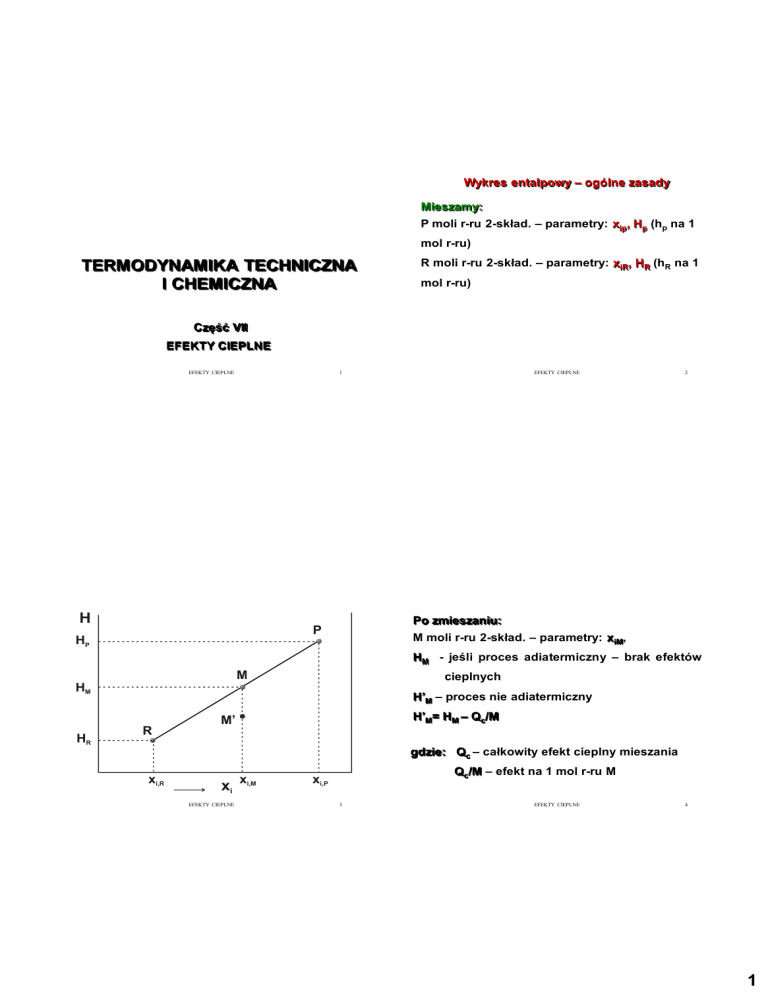
Wykres entalpowy – ogólne zasady
Mieszamy:
P moli r-ru 2-skład. – parametry: xip, Hp (hp na 1
mol r-ru)
TERMODYNAMIKA TECHNICZNA
I CHEMICZNA
R moli r-ru 2-skład. – parametry: xiR, HR (hR na 1
mol r-ru)
Część VII
EFEKTY CIEPLNE
EFEKTY CIEPLNE
1
H
2
Po zmieszaniu:
P
HP
EFEKTY CIEPLNE
M moli r-ru 2-skład. – parametry: xiM,
HM - jeśli proces adiatermiczny – brak efektów
M
cieplnych
HM
HR
H’M – proces nie adiatermiczny
R
H’M= HM – Qc/M
M’
gdzie: Qc – całkowity efekt cieplny mieszania
xi,R
xi xi,M
Qc/M – efekt na 1 mol r-ru M
xi,P
EFEKTY CIEPLNE
3
H
EFEKTY CIEPLNE
4
P
M
P’
R
M’
1
po dalszych przekształceniach:
Bilanse:
•masowy ogólny: M=P+R
•masowe składników: MxiM = Pxip + R XiR
•cieplny
(1)
P(HP-HM )=R(HM -HR)
(2)
P(xiP-xiM )=R(xiM -xiR)
stąd:
a) dla adiatermy
o
o
M HM = PHP + R HR
(3)
Eliminując M z (1) (2) poprzez (3)
otrzymujemy
HP  HM HM  HR

x iP  x iM x iM  x iR
(4)
z (4) wynika:
Reguła dźwigni: punkt M musi leżeć na prostej
łączącej R i P
(P+R) xiM = PxiP + R XiR
Położenie punktu M wynika z reguły dźwigni.
(P+R) HM = P HP + R HR
EFEKTY CIEPLNE
5
H
EFEKTY CIEPLNE
6
P
HP
M
HM
HR
M’
R
b) mieszanie nie-adiatermiczne
xi,R
x
xi i,M
P HP + R HR + Qc = HM’ M
H
Porównując (3) i (5) mamy:
xi,P
(5)
M HM = M HM’ - Qc
P
HM = HM’ - Qc/M
M HM = PHP + R HR
Wobec tego MM’ pokazuje efekt cieplny
mieszania diatermicznego P i R na 1 mol
roztworu.
M
P’
R
Prowadząc podobne przekształcenia uzyskać
można zależności do graficznej interpretacji:
M’
Qc/P – efekt cieplny mieszania na 1 mol r-ru P
Qc/R - efekt cieplny mieszania na 1 mol r-ru R
R’
EFEKTY CIEPLNE
7
EFEKTY CIEPLNE
8
xi
2
Uwaga: reguła linii prostej obowiązuje też dla
„trójek”:
Efekt cieplny mieszania (rozpuszczania) jest
równy zmianie entalpii mieszania:

RMP; RM’P’; PM’R’
Q  HM   x i ( Hi  Hi )
Praktyczne zastosowanie polega na tym, że znając
P, R oraz M’ można znaleźć M, P’ i R’ czyli
Qc/M; Qc/R i Qc/P
i
Q to całkowe ciepło mieszania (rozpuszczania)
Q odniesione jest do 1 mola roztworu, q do 1 kg;
Qi; qi do składnika „i”
Qi  xiQ; qi  uiq
EFEKTY CIEPLNE
9
Całkowity efekt cieplny to:
EFEKTY CIEPLNE

Zależności pomiędzy H, Hi a
Qc  n Q
10

Qi , Hi
Entalpia r-ru ciekłego (na 1 mol)
zależy od T, xi oraz p (wpływ p b. słaby)
H   x i Hi  Q
i
Używa się też różniczkowe ciepło rozpuszczania
z definicji cząstkowych wielkości molowych:



 Q 
Qi   c 
 ni  T ,p ,n
Q   xi Qi
H   x i Hi
i
i
Czyli:



 x i Hi   x i Hi   x i Qi   x i (Qi  Hi )
i
EFEKTY CIEPLNE
11
i
i
EFEKTY CIEPLNE
i
12
3
w końcu:


H
Hi  Qi  Hi
Q1
Interpretacja graficzna
Q2
H2
H1
H1
H2
x2
EFEKTY CIEPLNE
x2
13
EFEKTY CIEPLNE
14
faza parowa
H
izoterma
E
F
izobara skraplania
2-fazy
C
D
izobara wrzenia
A
faza ciekła
B
Ts
izoterma
podstawowa
X2, y2
Wyznaczanie całkowitego efektu
wykorzystując wsp. aktywności
H
Gi
 G  V
d
dP 
dT  
dxi

RT 2
 RT  RT
n RT
*
 G*  V *
H*
Gi
d
dP 
dT  
dxi

RT 2
n RT
 RT  RT
 GE  V E
HE
GE
d
dP 
dT   i dxi

2
RT
RT
RT
n RT


H E  H   xi H i
*
ZiE  Zi  Z i
 GE  V E
HE
d
dP 
dT   ln  i  dxi

2
RT
RT
RT
n


 ln  i  
H iE
 

RT 2
 T  P ,x
Ciepło rozcieńczania qI-II – efekt cieplny
izotermicznego
rozcieńczania
roztworu
rozpuszczalnikiem od stanu I do II
mieszania
GiE  RTln i
Sposób konstrukcji:
Dane:
1) zależność Q = f(xi) dla jednej temperatury Ts
 ln  i  
Vi E
 

RT
 p T ,x
(podstawowej)
V E  V   xiVi
EFEKTY CIEPLNE
Wykres entalpowy dla równowagi f. ciekła – f.
parowa; (2 składniki)
2) zależności ccp1, ccp2 od temperatury oraz
15
zależność cpM od temperatury
EFEKTY CIEPLNE
16
4
H
Q1
Q2
H2
H1
H1
H2
x2
x2
faza parowa
założenia:
H
•niskie ciśnienie (brak wpływu p na H)
•stan odniesienia H (T=273K; p= 1 bar) =0
izoterma
E
F
izobara skraplania
2-fazy
C
obliczamy:
D
T0
izobara wrzenia
A
faza ciekła
B
Ts
XEFEKTY
2, yCIEPLNE
2
izoterma
podstawowa
HM   x iHi  Q
i 1,2
17
izotermy dla TTs obliczamy z:
Ts
Hi   cpidT; i  1,2
dla Ts – jest to izoterma na
wykresie H=f(x)
EFEKTY CIEPLNE
18
Konstrukcja izobar, izoterm w obszarze 2fazowym i parowym
T
HM  HM (Ts )   cpMdT
Dane:
Ts
•ciepła parowania Lp1, Lp2
•zależności cgp1, cgp2, cpM od temperatury
•temperatury wrzenia czystych składników 1 i 2
•zależność temperatur wrzenia i skraplania dla
roztworu w zależności od x2, y2
EFEKTY CIEPLNE
19
EFEKTY CIEPLNE
20
5
Izobarę wrzenia obliczamy następująco:
Izobarę skraplania obliczamy następująco:
a) obliczamy H składników w temperaturze
a) obliczamy H składników w temperaturze
wrzenia (p-ty C, D)
b) obliczamy pozostałe punkty na linii wrzenia
znając temperatury wrzenia i ciepła właściwe
roztworu ciekłego dla różnych stężeń.
Tw
HM  HM (Ts )   cpMdT
skraplania dodając ciepła
entalpii wrzenia (p-ty E, F)
parowania
do
b) obliczamy pozostałe punkty na linii wrzenia
znając temperatury skraplania i ciepła
właściwe roztworu parowego dla różnych
stężeń
Tskr
p
HM  HM (Tw)   cpM
dT
Ts
Tw
EFEKTY CIEPLNE
21
EFEKTY CIEPLNE
22
Izotermy w fazie parowej
Ze
względu
na
prawie
zerowe
ciepła
rozpuszczania izotermy są prostoliniowe –
wystarczy
obliczyć
entalpie
czystych
składników dla różnych wartości temperatury.
Izotermy w obszarze 2-fazowym
Są to linie proste łączące składy równowagowe.
EFEKTY CIEPLNE
23
6