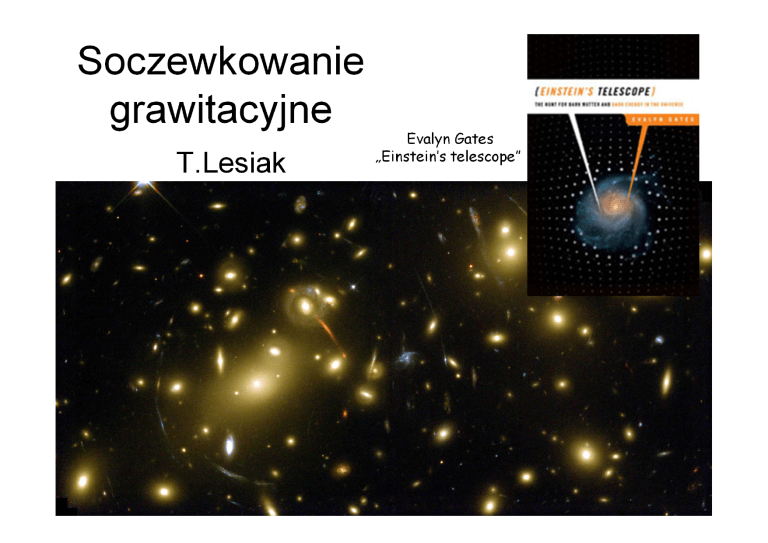
Soczewkowanie
grawitacyjne
T.Lesiak
Evalyn Gates
„Einstein’s telescope”
Zamiast wstępu
Miraże optyczne
a
soczewki grawitacyjnene
Wskutek odbicia światła od powierzchni wody
oraz jego załamania, obserwator widzi dwa
obrazy drzewa: rzeczywisty (A) i miraż (A’)
T.Lesiak
Soczewki grawitacyjne
Masywny obiekt (galaktyka G),
umieszczony między
obserwatorem i źródłem (A),
odchyla, deformuje
i zwielokrotnia obrazy źródła.
2
Zamiast wstępu
„Odkształcenia struktury przestrzeni działają jak grawitacyjne soczewki, które
zmieniają kierunek biegu światła, w taki sam sposób jak mniej egzotyczne soczewki
wykonane ze szkła lub plastiku”
Evalyn Gates
Tak jak obrazowanie metodami rezonansu
magnetycznego, PET, itp. umożliwiło lekarzom
oglądanie wnętrza ciała ludzkiego w sposób, który
był nie do pomyślenia jeszcze 100 lat temu…
tak soczewki grawitacyjne, wynikające z ogólnej
teorii względności dają astronomom nowe
możliwości oglądania wszechświata.
T.Lesiak
Soczewki grawitacyjne
3
Klasyczny test OTW:
zakrzywienie światła w pobliżu Słońca
Przewidywanie, iż światło gwiazd ulega zakrzywieniu w pobliżu Słońca
– to ostatnie działa jak soczewka grawitacyjna
T.Lesiak
Soczewki grawitacyjne
4
Klasyczny test OTW:
zakrzywienie światła w pobliżu Słońca
Przy obecności Słońca, pozycja
odległej gwiazdy wydaje się odsuwać
od swego rzeczywistego położenia.
„Gravity does not `pull’. Rather, space pushes” – Michio Kaku
Grawitacja nie „przyciąga”, to raczej przestrzeń „odpycha”.
T.Lesiak
Soczewki grawitacyjne
5
Klasyczny test OTW:
zakrzywienie światła w pobliżu Słońca
Gwiazda obserwowana w pobliżu tarczy słonecznej powinna być przesunięta względem
swojego „normalnego” położenia na niebie.
Obserwacje gwiazd w pobliżu tarczy słonecznej możliwe jedynie podczas zaćmień.
Trzy (historycznie ważne) ekspedycje mające na celu obserwacje zaćmień Słońca:
1. Erwin Freundlich (Krym, sierpień 1914 r.) – obserwacje przerwane wybuchem wojny
i niewolą uczestników; wielkie szczęście dla OTW, gdyż w tym czasie przewidywania
Einsteina dla kąta ugięcia promienia światła przez Słońce zawierały błąd o czynnik 2.
2a. Arthur Eddington (Wyspa Książęca, wybrzeże Afryki Zachodniej, wiosna 1919r.);
Słońce wyjrzało zza chmur jedynie na krótką chwilę – jeden zestaw danych
2b. Andrew Crommelin (Sobral, Brazylia, wiosna 1919 r.); aparatura dała nieostre
obrazy z powodu jej wrażliwości na zmiany temperatury; dwa zestawy danych: „z
dużego” i „małego teleskopu”.
Pierwsze obrazy ok. tuzina gwiazd (z gromady Hiad) obserwowane przez soczewkę
grawitacyjną wytworzoną przez masę Słońca
T.Lesiak
Soczewki grawitacyjne
6
Klasyczny test OTW:
zakrzywienie światła w pobliżu Słońca
Porównanie obrazów Eddingtona i Crommelina z fotografiami tych samych gwiazd
wykonanymi w nocy (gdy na położenie gwiazd nie wpływa zakrzywienie czasoprzestrzeni.
Wynik: przesunięcie o 1.74 sekundy kątowej z błędem 20% - zgodnie z OTW
(obecna precyzja 1%)
Kontrowersje:
analiza danych, dokonana przez Eddingtona mogłaby być zakwestionowana:
Sobral: mały teleskop: 1.98 ± 0.12
Wyspa Książeca:
1.61 ± 0.30
Sobral duży teleskop: 0.93 ± ??
jakość danych:
Eddington ogłosił wszystkie trzy wyniki, zaznaczając, iż trzeci jest tak słabej
jakości, iż nie uwzględnia go w średniej
Times, 6.XI 1919r.
„REWOLUCJA W NAUCE: Nowa teoria Wszechświata: idee Newtona odrzucone”
Słońce stało się w ten sposób pierwszą znaną nam soczewką grawitacyjną…
T.Lesiak
Soczewki grawitacyjne
7
Dalsza, krótka historia soczewkowania
grawitacyjnego
Eddington 1919-20r.: „pole grawitacyjne wokół cząstki będzie działać jak soczewka
skupiająca”; po drugiej stronie soczewki powstaną „obrazy poboczne”.
Orest Chwolson 1924r.: rozważa możliwość obserwowania „fikcyjnych gwiazd podwójnych”
gdy światło odległej gwiazdy jest soczewkowane przez inny obiekt;
zauważa, iż w pewnych warunkach soczewkowanie może
rozszczepić punktowy promień świetlny w pierścień.
Einstein 1936r.: - artykuł w Science pt. „Działanie gwiazdy jako soczewki dzięki ugięciu
światła w polu grawitacyjnym” (inspiracja Rudiego Mandla):
1. pełna idea soczewkowania jednej gwiazdy przez drugą, włączając w to istnienie obrazów
podwójnych i tworzenie pierścienia świetlnego,
2. uwaga, iż soczewkowanie to „najdziwniejszy efekt” pozbawiony praktycznego znaczenia
„…oczywiście nie ma nadziei na zaobserwowanie tego zjawiska bezpośrednio”.
Zwicky 1937r.: dwa listy do Physical Review z ważnymi obliczeniami:
„Galaktyki to lepsze soczewki niż gwiazdy:
Ich soczewkowanie może być narzędziem dalszych testów OTW oraz rozszerza zasięg
obserwacji a inaczej niedostępne rejony Wszechświata poprzez powiększanie odległych galaktyk
oraz pozwala na bardziej „bezpośrednie wyznaczanie” mas galaktyk.”
Jego (prawdziwa) opinia: „prawdopodobieństwo wykrycia mgławic, które wytwarzają
soczewkowanie grawitacyjne, stanie się praktycznie pewnością.”
T.Lesiak
Soczewki grawitacyjne
8
Soczewkowanie grawitacyjne a kwazary
Druga po Słońcu soczewka grawitacyjne została odkryta dopiero w 1979 r. …
Obserwacja kwazara QSO 0957+561
(pierwsze kwazary odkryto w 1963r.)
Dokładniejsze badania:
1. dwa bliźniacze źródła światła „A” i „B”,
odległe od siebie o ok. 6 sekund kątowych.
2. oba obiekty znajdują się w tej samej
odległości od Ziemi (ok 6 mld ly).
3. Ich linie spektralne są identyczne.
Źródła A i B to dwa obrazy tego samego kwazara,
spowodowane obecnością między nim a Ziemią
(początkowo niewidocznej) galaktyki
T.Lesiak
Soczewki grawitacyjne
9
Elementarz soczewkowania
grawitacyjnego czyli „teleskopu Einsteina”
„Soczewka” znajduje się między
obserwowanym obiektem a Ziemią.
Jest ona „rzeźbiona” w czasoprzestrzeni
poprzez odpowiedni rozkład jej masy.
Geometria soczewki (jej kształt i rozmiar)
decyduje o efekcie jaki wywiera ona na światło
przez nią przechodzące.
Znajomość geometrii soczewki wiedza
o powodowanym przez nią zakrzywieniu
czasoprzestrzeni informacja o tym jaką drogą
światło podąża w pobliżu soczewki
Najczęściej przedmiotem badań/poszukiwań jest sama soczewka
Kluczowe jest to, iż jej działanie jest całkowicie opisywalne jedynie przez rozkład masy.
Większość soczewek jest ciemna lub ma ciemną składową (jak większość masy Wszechświata).
Soczewkowanie umożliwia, w szczególności, określenie masy całej galaktyki lub odkrycie czarnej
dziury dzięki śladom jakie zostawia ona w czasoprzestrzeni wokół niej.
T.Lesiak
Soczewki grawitacyjne
10
Soczewkowanie grawitacyjne
a kieliszek (do) wina
Podstawy geometrii soczewkowania grawitacyjnego
są bardzo podobne do optyki geometrycznej
soczewek zbudowanych ze szkła lub plastiku…
W przypadku szkieł optycznych ugięcie światła jest
spowodowane krzywizną powierzchni rozdzielającej
ośrodki i różnicą prędkości rozchodzenia się w nich
światła (zmianą współczynnika załamania – światło
niebieskie rozchodzi się wolniej niż czerwone)
T.Lesiak
Soczewki grawitacyjne
11
Soczewkowanie grawitacyjne
a poszukiwanie ciemnej materii
Efekt soczewkowania grawitacyjnego jest wynikiem zakrzywienia czasoprzestrzeni.
W odróżnieniu od szkła, na ugięcie nie ma wpływu materiał, przez który przechodzi światło,
Wpływ ten posiada natomiast sposób zmian pola grawitacyjnego.
Światło zwalnia w polu grawitacyjnym, lecz efekt ten nie jest zależny od koloru światła.
Najprostsza soczewka grawitacyjna składa się z pojedynczego masywnego obiektu, którego
rozmiary są zaniedbywalnie małe w porównaniu do skal odległości występujących między
źródłem i obserwatorem.
Obraz wytworzony przez taką soczewkę zależy od:
- masy obiektu występującego w roli soczewki
(jak wielkie zniekształcenie czasoprzestrzeni obiekt powoduje),
- ułożenia obiektu i soczewki względem siebie
(najsilniejsze soczewkowanie wówczas gdy soczewka znajduje się dokładnie przed obiektem),
- odległości między źródłem, soczewką i obserwatorem (efekt maksymalny wtedy,
gdy soczewka znajduje się w połowie odległości między źródłem i obserwatorem).
T.Lesiak
Soczewki grawitacyjne
12
Soczewkowanie grawitacyjne
a poszukiwanie ciemnej materii
Światło w pobliżu masywnego obiektu podąża najkrótszą drogą w zakrzywionej przez obiekt
czasoprzestrzeni.
Wielkość ugięcia określa kąt pomiędzy prostą, po której światło się rozchodziło (z dala od
masywnego obiektu), a kierunkiem, w którym się ono propaguje po przejściu w pobliżu masy.
Wartość kąta ugięcia wynika z równań Einsteina:
M – masa obiektu
b – parametr zderzenia
c – prędkość światła
G – stała Newtona
Rs – promień Schwarzschilda
Obraz powstały w wyniku soczewkowania, obserwowany w ziemskim teleskopie stanowi rodzaj
złudzenia optycznego: światło wydaje się docierać z punktu na niebie, który jest przesunięty
względem położenia, w którym obiekt powinien się znajdować przy nieobecności masy soczewki.
T.Lesiak
Soczewki grawitacyjne
13
Pierścień Einstena
Ten typ soczewkowania pojawia się gdy źródło światła, soczewka i obserwator znajdują się
dokładnie na linii prostej, a soczewka jest położona w połowie odległości między źródłem
i obserwatorem.
Pierwsza obserwacja:
W takim przypadku światło wychodzące ze
Jacqueline Hewitt et al., 1987 r.
źródła może poruszać się
jednocześnie w wielu kierunkach, podążając
po trajektoriach, które zakrzywiają się
i ostatecznie kończą w jednym miejscu
(naszej obserwacji).
Sama soczewka jest niewidoczna na zdjęciu.
Źródło – galaktyka świecąca jasno w zakresie
radiowym, z centralnym jądrem oraz dwom
„listkami” rozkładu fal radiowych rozchodzącymi
się z obu stron jądra.
Soczewka leży bezpośrednio przed jednym z
listków rozkładu fal radiowych i wytwarza dwa
obrazy jądra galaktyki (jasne plamy) oraz
pierścień światła.
T.Lesiak
Soczewki grawitacyjne
14
Pierścień Einstena
Projekt SDSS (Sloan Digitan Sky Survey): osiem kolejnych pierścieni 2006 r.
Soczewki – galaktyki eliptyczne odległe od Ziemi 2-4 miliony ly – widoczne na
zdjęciach jako pomarańczowo-żółte elipsy w środku „byczego oka”.
Niebieskawe pierścienie (otaczające soczewki)
– galaktyki znajdujące się za soczewką, położone od nas dwa razy dalej niż soczewki.
T.Lesiak
Soczewki grawitacyjne
15
Pierścień Einstena
T.Lesiak
Soczewki grawitacyjne
16
Pierścień Einsteina
W przeciwieństwie do
soczewek optycznych,
zaprojektowanych tak,
aby odtwarzać w ognisku
obraz pierwotny jak najwierniej,
każda część soczewki
grawitacyjnej ma swoje
własne ognisko.
Każdy element soczewki
grawitacyjnej odchyla
przechodzące przez nią światło
w różnych kierunkach zależnie
od kąta padania i tego, która jej
część przechwytuje światło.
Na Ziemi widzimy pierścień
tj. tylko tę część światła, która
została skierowana do miejsca
obserwacji.
T.Lesiak
Soczewki grawitacyjne
17
Pierścień Einsteina
T.Lesiak
Soczewki grawitacyjne
18
Pierścień Einsteina
Problem: nie możemy przesuwać soczewki (np. galaktyki) w przestrzeni w poszukiwaniu
obrazów jakie ona dostarcza.
Zamiast tego można wykonać symulacje komputerowe:
Oryginał:
niesoczewkowany znak
zapytania
Soczewka leży bezpośrednio
przed znakiem zapytania
i powstaje pierścień Einsteina
Soczewka jest nieco
przesunięta na lewo od
znaku zapytania i powstają
dwa obrazy (jeden z nich
jest odwrócony)
Niewidzialna soczewka
znajduje się na lewym
brzegu ramki i widoczny jest
tylko efekt słabego
soczewkowania
(obraz znaku zapytania
lekko zniekształcony
i przesunięty trochę na
prawo)
T.Lesiak
Soczewki grawitacyjne
19