Document

D2. WYZNACZANIE WZGLĘDNYCH PRZENIKALNOŚCI
ELEKTRYCZNYCH I STRAT
część teoretyczną opracowała: Bożena Janowska-Dmoch
część eksperymentalną opracował: Marek Pękała
Dielektrykami (izolatorami elektrycznymi) nazywa się substancje, w których elektrony
są zlokalizowane (związane) na atomach. W dielektrykach nie występują elektrony
swobodne, które w metalach odpowiadają za przewodnictwo elektryczne. W atomach lub
cząsteczkach dielektryka umieszczonego w polu elektrycznym następują zmiany w rozkładzie
ładunków wewnątrz dielektryka poprzez indukowanie dipoli elektrycznych lub
porządkowanie własnych dipoli równolegle do linii sił zewnętrznego pola. Proces ten
nazywamy polaryzacją dielektryka. Wyróżniamy następujące rodzaje polaryzacji:
elektronową, jonową i orientacyjną. Skutkiem polaryzacji jest zmniejszenie się natężenia
pola elektrycznego wewnątrz dielektryka. Makroskopowe własności dielektryków opisuje
wielkość fizyczna nazywana przenikalnością elektryczną . Generalnie przenikalność
elektryczna nie jest stałą, jej wartość zależy od temperatury. W silnych polach elektrycznych
przenikalność elektryczna, dla pewnej grupy substancji zwanej dielektrykami nieliniowymi,
zależy od natężenia pola elektrycznego. W zmiennym polu elektrycznym przenikalność
elektryczna zależy jeszcze od częstotliwości zmian pola elektrycznego. W polu
elektrostatycznym lub w polach wolnozmiennych przenikalność elektryczna jest wielkością
rzeczywistą, natomiast w polach szybkozmiennych wygodnie jest posługiwać się pojęciem
zespolonej przenikalności elektrycznej.
Gdy kondensator wypełniony dielektrykiem podłączymy do źródła zmiennego
napięcia, to zmiany napięcia powodują zmiany polaryzacji dielektryka nazywane prądem

przesunięcia. Oprócz prądu przesunięcia, który wyprzedza w fazie przyłożone napięcie o ,
2
do okładek kondensatora może dopływać prąd zgodny w fazie z napięciem. Prąd ten
świadczy o stratach energii przy polaryzacji dielektryka. Energia ta rozprasza się w
dielektryku i ujawnia się w postaci ciepła, co można by obserwować mierząc wzrost
temperatury dielektryka umieszczonego w kalorymetrze. Aby uwzględnić efekty polaryzacji i
strat w dielektryku wprowadza się zespoloną przenikalność elektryczną:
ˆ     i  ,
gdzie   jest względną przenikalnością elektryczną, zaś   jest czynnikiem strat. Obecność
strat dielektryka powoduje zmianę różnicy faz  między napięciem i natężeniem prądu. Staje

się ona mniejsza niż
. Miarą opóźnienia zmian polaryzacji dielektryka w stosunku do
2
zmian pola elektrycznego jest tangens kąta strat zdefiniowany jako:
tg  
 

i nazywany współczynnikiem strat dielektrycznych.
Jeżeli kondensator wypełniony dielektrykiem podłączymy do źródła wytwarzającego
zmienne sinusoidalnie napięcie U  U 0 cos  t , to w kondensatorze powstaje zmienne
 
sinusoidalnie pole elektryczne o natężeniu E  E0 cos  t . Indukowane w dielektryku zmiany
2
rozmieszczenia ładunków, opisane przez wektor indukcji elektrycznej D (zwany także
wektorem przesunięcia), nie zachodzą natychmiastowo, lecz są przesunięte w fazie względem
natężenia pola elektrycznego o kąt , czyli
 
D  D0 cos t    ,

gdzie D0 jest amplitudą zmian wektora indukcji.
Zachowanie dielektryków w przemiennym polu elektrycznym najwygodniej jest
opisywać posługując się liczbami zespolonymi. Przyłożone napięcie jest częścią rzeczywistą
pewnej liczby zespolonej U  U 0 e i t , a natężenie pola elektrycznego jest częścią rzeczywistą


 
liczby zespolonej E  E0 e i t . Relację między zespolonymi wektorami D i E można zapisać
w postaci


D   0ˆ E ,
gdzie ˆ     i  oznacza zespoloną przenikalność elektryczną dielektryka. Z własności liczb
zespolonych wiadomo, że ˆ     i    e i , gdzie     2    2 , a e i  cos   i sin  .
Wektor indukcji zapiszemy




D   0ˆ E   0  E0 e i t e i  D0 e i  t   ,


gdzie D0   0  E0 jest amplitudą wektora indukcji elektrycznej i tak, jak wspomniano wyżej
wektor indukcji jest przesunięty w fazie względem natężenia pola elektrycznego. W ośrodkach


jednorodnych wektor D jest równoległy do wektora E i zespoloną przenikalność elektryczną
możemy przedstawić wzorem
ˆ 
D0 e i t e i
D
 0 cos   i sin       i  .
i t
 0 E0
 0 E0 e
Równanie to jest równoważne dwóm następującym równaniom, które muszą być spełnione
jednocześnie (część rzeczywista po lewej stronie równania musi być równa części rzeczywistej
po prawej stronie i analogicznie dla części urojonych)
 
a stąd
D0
cos 
 0 E0
  
tg  
 
.

D0
sin  ,
 0 E0
(1)
Indukcję elektryczną można rozdzielić na dwie składowe. Jedną składową jest indukcja


elektryczna próżni  0 E , drugą składową jest polaryzacja dielektryka P równa co do wartości
gęstości powierzchniowej ładunku indukowanego w dielektryku, czyli

 
D  0E  P .
3
Jeśli w jednostce objętości dielektryka znajduje się N elementarnych dipoli, każdy o momencie

dipolowym p i , to wektor polaryzacji możemy przedstawić jako wartość średnią sumy
wektorowej tych momentów dipolowych

P
N

p
i 1
.
i
Gdy dielektryk jest izotropowy i gdy brak zewnętrznego pola elektrycznego, to polaryzacja jest
równa zero, bo dipole są rozłożone bezładnie i żaden kierunek nie jest uprzywilejowany.
Natomiast w zewnętrznym polu elektrycznym na każdy z dipoli działa moment siły, który dąży
aby ustawić dipol zgodnie z kierunkiem pola a jednocześnie pole elektryczne indukuje w
cząsteczce dodatkowy moment dipolowy. Wektor polaryzacji definiujemy jako moment
dipolowy jednostki objętości tej substancji, czyli

P  lim
1
V 0 V
N

p
i 1
i
.
W idealnym dielektryku, gdzie nie ma swobodnych ładunków  r  0 , ciągłe zmiany
pola elektrycznego powodują ciągłe przesunięcia ładunków polaryzacyjnych, które nazywamy
prądem przesunięcia. Gęstość prądu przesunięcia jest równa prędkości zmian wektora indukcji
elektrycznej

 i t
 i t
 i   t  2 

D 

jD 

  0 E0 e  i   0 E0 e     0 E0 e 
t t

Prąd przesunięcia wyprzedza w fazie napięcie o
. Gęstość prądu przesunięcia zależy od
2
częstości  , czyli w polu elektrostatycznym prądu przesunięcia nie ma.
W rzeczywistych dielektrykach, gdzie    0 , wystąpi dodatkowa składowa zgodna w
fazie z napięciem zwana prądem przewodzenia (lub prądem strat). Gęstość prądu
przewodzenia jp wyraża postać mikroskopowa prawa Ohma




j p  E
Współczynnik  nazywamy przewodnictwem właściwym danej substancji.
Wypadkowa gęstość prądu płynącego w obwodzie zawierającym kondensator z
dielektrykiem jest sumą prądu przesunięcia i przewodzenia


 

j  j D  j p  i  0 E  E .
Obliczając gęstość prądu wynikającą z prędkości zmian wektora indukcji elektrycznej z
uwzględnieniem strat otrzymujemy równanie





 D 
j

ˆ 0 E  i ˆ 0 E  i   0 E    0 E .
t t


4
Z porównania obu zależności wynika związek między czynnikiem strat a przewodnictwem
dielektryka

  
.
(2)
 0
Cel
Celem ćwiczenia jest wyznaczenie, dla wybranych ciał stałych, przenikalności
elektrycznej   , współczynnika strat dielektrycznych tg  oraz przewodnictwa
właściwego  .
Wymagania
Momenty dipolowe molekuł, dipol w polu elektrycznym. Dielektryki polarne i niepolarne,
dielektryk w polu elektrycznym. Rodzaje polaryzacji dielektryków. Wektor natężenia pola
elektrycznego, wektor indukcji elektrycznej, wektor polaryzacji, przenikalność dielektryczna,
pojemność elektryczna kondensatorów. Kondensator w obwodzie prądu przemiennego. Prawo
indukcji Faradaya, SEM indukcji. Obwód RLC, rezonans, kształt krzywej rezonansowej a
straty w obwodzie. Pochłanianie energii w dielektryku. Prawa Ohma i Kirchhoffa.
Literatura
A. Chełkowski, Fizyka dielektryków, PWN
T. Krajewski, Zagadnienia fizyki dielektryków, WKŁ.
K. Zboiński, Laboratorium z fizyki, Liber
Sz. Szczeniowski, Fizyka doświadczalna, cz.III, Elektryczność i magnetyzm, PWN.
H. Szydłowski, Pracownia fizyczna , PWN.
Opis układu
Metody
pomiaru
generator 1,2 MHz ze
obwód rezonansowy RLC
podstawowych
parametrów
wzmacniaczem
dielektryków, czyli   i tg  , są
V
różne dla
różnych
zakresów
częstotliwości pola elektrycznego.
W
obszarze
częstotliwości
radiowych,
104  108 Hz,
Cz
stosuje się metody rezonansowe.
~
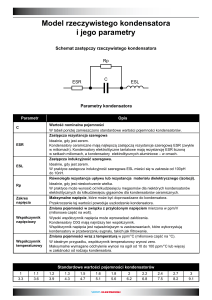
Obwód rezonansowy składa się z
cewki indukcyjnej i połączonych
Cx
ze sobą równolegle dwóch
kondensatorów.
Jednym z nich jest kondensator pomiarowy o pojemności C0, który może być
wypełniany badanymi dielektrykami, a wtedy jego pojemność zmienia się na Cx, drugim jest
kondensator o regulowanej pojemności Cz z precyzyjnym odczytem zmiany pojemności. Do
części uzwojenia cewki tego obwodu jest włączony woltomierz służący jako wskaźnik
dostrojenia.
Obwód rezonansowy jest słabo sprzężony indukcyjnie z generatorem prądu
przemiennego o częstotliwości 1,2 MHz. Prąd przemienny płynący w obwodzie generatora
5
wytwarza w cewce zmienny w czasie strumień indukcji magnetycznej. Część tego strumienia
wnika do cewki obwodu rezonansowego indukując w niej siłę elektromotoryczną indukcji
(SEM). Wartość siły elektromotorycznej indukowanej w obwodzie rezonansowym zależy od
zgodności częstości drgań własnych obwodu z częstością pracy generatora. Optymalne
dostrojenie do rezonansu jest sygnalizowane przez maksimum napięcia na woltomierzu w
obwodzie pomiarowym.
Istota pomiaru polega na dostrojeniu pojemności obwodu rezonansowego do
rezonansu najpierw dla pustego kondensatora o pojemności C0, a po wypełnieniu tego
kondensatora dielektrykiem ponownie dostraja się obwód do rezonansu dla pojemności Cx.
Kształt krzywej rezonansowej pozwala wyznaczyć współczynnik strat dielektrycznych tg 
danej substancji.
Jako kondensator o regulowanej pojemności zastosowano układ dwóch
współosiowych cylindrów o różnej średnicy, przesuwanych wzajemnie przy pomocy śruby
mikrometrycznej. Jego pojemność jest liniową funkcją wskazania śruby mikrometrycznej,
przy czym wkręcenie śruby o 1 mm zwiększa pojemność o 1,4 pF, zaś wykręcenie śruby
zmniejsza pojemność o tę samą wartość.
Wyprowadzenie wzorów
Pomiar przenikalności elektrycznej
Częstość obwodu generatora jest w naszym ćwiczeniu stała. Do niej musi być
dopasowana częstość własna obwodu rezonansowego, więc dla ustalonej geometrii układu
częstość rezonansowa obwodu pomiarowego jest również wielkością stałą. Częstość ta zależy
od indukcyjności L i całkowitej pojemności C obwodu. Słabo tłumiony obwód RLC jest w
rezonansie, gdy częstość drgań jest równa

1
LC
.
Wtedy na indukcyjności L pojawia się maksymalna siła elektromotoryczna, co można
stwierdzić obserwując wskazania woltomierza. W skład pojemności całkowitej obwodu
wchodzą: pojemność kondensatora pomiarowego Cp, pojemność kondensatora zmiennego Cz
i pojemność rozproszona obwodu Cr. Kondensatory są połączone ze sobą równolegle, czyli
C  C p  C z  Cr .
Zmieniając pojemność Cz i notując wskazania woltomierza uzyskujemy dla kondensatora
pomiarowego zależność U(Cz) nazywaną krzywą rezonansową.
Oznaczmy przez C0 pojemność pustego kondensatora płaskiego. Pusty kondensator
oznacza, że przestrzeń między jego okładkami jest wypełniona powietrzem. Przenikalność
elektryczna powietrza w temperaturze pokojowej jest równa    1,005 i tylko 0,5% różni się
od przenikalności elektrycznej próżni. Pojemność pustego kondensatora płaskiego wyraża się
wzorem
 S
C0  0 ,
d
gdzie S jest powierzchnią okładek, zaś d jest odległością między okładkami.
6
Po wypełnieniu kondensatora pomiarowego dielektrykiem o przenikalności elektrycznej
   1 jego pojemność wzrośnie   razy
C p   C 0
co spowoduje przyrost pojemności o C p     1C 0 .
Jeśli początkowo dostroimy układ do rezonansu dla pustego kondensatora
pomiarowego pojemnością kondensatora zmiennego równą Cz1, to dla kondensatora z
dielektrykiem rezonans wystąpi dla mniejszej pojemności Cz2 takiej, która skompensuje
przyrost C p , czyli
C z 2  C z1  C p

C z  C p
C z 2  C z1     1C0
   1
C z 2  C z1
,
C0
Jeśli rezonans dla kondensatora pustego występuje w położeniu l1 śruby
mikrometrycznej kondensatora zmiennego, a dla kondensatora wypełnionego dielektrykiem
w położeniu l2, to
C z 2  C z1  A  l2  l1 , gdzie A jest stałą aparaturową: A  1,4
pF
mm
pF 

1,4
  l 2  l1 
mm 

  1
.
C0
Wyznaczanie strat dielektrycznych
Współczynnik strat dielektrycznych
tg  
 
wyznaczamy z kształtu krzywej

1 

, gdzie Q jest współczynnikiem dobroci obwodu
Q  rez
rezonansowego (patrz np. instrukcja ćwiczenia E3). Jeżeli pojemność obwodu rezonansowego
1
C h od pojemności rezonansowej Crez, to napięcie wskazywane przez
różni się o
2
woltomierz będzie mniejsze od napięcia w rezonansie. Korzystając z tego, że krzywa
rezonansowa jest symetryczna, możemy wyznaczyć różnicę pojemności Ch dla dwóch
punktów na zboczach krzywej rezonansowej, leżących symetrycznie po obu stronach
U
maksimum, w położeniach, dla których mierzone napięcie będzie równe U  max (warunek
2
połowy mocy traconej podczas rezonansu, a moc ~ U2), wtedy
rezonansowej, bo
tg 
7





 2  1
1  1
1 
1 
1
1
tg  






 rez
 rez  LC 2
LC1   rez  
C h 
C h  

L C rez 

 L C rez  2 
2  








1
1
1




 rez 




C h
C h 

 
LC rez 1 
 LC rez 1 

2
C
2
C
rez 
rez  



1
Gdy Ch << Crez, to z rozwinięcia w szereg Taylora wynika, że
1
1
1
C h
 1
C h
 1
1 C h
, zaś
2 C rez
2C rez
1 C h
, a wtedy
2 C rez
2C rez
tg 
C h
2C rez
(3)
Pojemność rezonansowa naszego obwodu pomiarowego jest równa C rez  195 pF . Jest ona
sumą pojemności kondensatora pomiarowego Cp, pojemności kondensatora zmiennego Cz i
pojemności rozproszonej obwodu Cr.
Straty dielektryka wypełniającego kondensator wyznaczamy z różnicy między
stratami obwodu z kondensatorem zawierającym dielektryk 1  1 tg 1 i bez dielektryka
 2  tg 2 , czyli przy pomocy wzorów (1) i (3) otrzymujemy:
   1tg1  tg 2 ,
a przy pomocy wzoru (2) dochodzimy do wzoru na przewodnictwo dielektryka
   0  .
Wykonanie ćwiczenia
W części doświadczalnej dokonuje się rejestracji krzywych rezonansowych, czyli
zależności napięcia U od pojemności C, dla kondensatora wypełnionego badanym
dielektrykiem o grubości d i pustego powietrznego kondensatora o takiej samej odległości
okładek.
Z zarejestrowanych krzywych rezonansowych wyznacza się dwa parametry:
pojemność rezonansową Crez, przy której napięcie osiąga maksimum Umax = Urez, oraz tzw.
szerokość połówkową Ch, czyli różnicę pojemności Ch = C1  C2 pomiędzy
pojemnościami C1 i C2, dla których U(C1) = U(C2) = Umax/ 2 .
8
Wyniki wszystkich pomiarów muszą być zapisane w sprawozdaniu, opatrzone odpowiednimi
jednostkami i podpisane przez asystenta.
Uwaga 1: włączenia napięcia zasilania i dobór parametrów układu zapewniających
właściwe sprzężenie obwodów dokonuje asystent (odległość między cewkami
powinna być większa niż 14 cm).
Uwaga 2: układy generatora, zasilacza oraz woltomierz są układami lampowymi i
wymagają kilku minut nagrzewania dla ustalenia parametrów.
Pomiary z kondensatorem płaskim
a) Wkręcamy śrubę regulującą odległość między okładkami kondensatora płaskiego
i doprowadzamy do zetknięcia metalowych okładek kondensatora. W tym położeniu
czujnik mikrometryczny powinien wskazywać zero. Możliwa jest korekta zerowania
czujnika przez obrót śrubki umieszczonej na szczycie czujnika.
b) Między okładkami kondensatora umieszczamy dielektryk. Odległość między
okładkami d równą grubości dielektryka odczytujemy na czujniku mikrometrycznym.
c) Zapisujemy grubość i nazwę próbki.
d) Sprawdzamy, czy przełącznik zakresów woltomierza lampowego jest ustawiony na
zakresie 300 mV.
Uwaga! W pomiarach krzywej rezonansowej wystarcza rejestracja względnych
wartości napięcia, więc żeby podnieść dokładność odczytu wskazania przyrządu
można odczytywać z górnej skali o zakresie 0 – 1000 działek na najwyższym
zakresie woltomierza.
e) Obracając śrubą mikrometryczną kondensatora zmiennego znajdujemy na
woltomierzu maksimum napięcia rezonansowego U max  U rez .
f) Prawym niebieskim pokrętłem zasilacza dobieramy taki prąd anodowy zasilacza, aby
przy napięciu rezonansowym, wskazówka woltomierza znalazła się w zakresie 940990 działek na najwyższej skali.
g) Wykręcamy śrubę mikrometryczną zmniejszając napięcie do 900 działek, a następnie
co 100 aż do 200 działek notujemy wskazania woltomierza U i położenia śruby
kondensatora l.
h) Powracamy do położenia rezonansu, a następnie wkręcając śrubę mikrometryczną
zmniejszamy napięcie do 900 działek, a następnie . co 100 aż do 200 działek
notujemy wskazania woltomierza U i położenia śruby kondensatora l.
Propozycja zapisu wyników:
Położenie
lmax = .........
Nazwa próbki i
odległość między
okładkami d
[jednostka]
Umax = ..........
Położenie śruby
mikrometrycznej l1
poniżej rezonansu
[mm]
Napięcie U
[działki]
Położenie śruby
mikrometrycznej l2
powyżej rezonansu
[mm]
9
i) Żeby zmierzyć tzw. szerokość połówkową Ch odstrajamy układ od rezonansu tak,
U max U rez

aby napięcie spadło do wartości
i notujemy położenia śruby
2
2
mikrometrycznej po obu stronach rezonansu, dla których warunek ten jest spełniony.
j) Dla każdej próbki zapisujemy błędy systematyczne d, l, U wynikające z
dokładności przyrządu.
k) Wyjmujemy dielektryk. i przed rozpoczęciem pomiarów dla każdej próbki
sprawdzamy czy czujnik mikrometryczny wskazuje zero przy zetknięciu okładek
kondensatora.
l) Ustawiamy okładki kondensatora w odległości równej grubości poprzednio badanego
dielektryka.
m) Powtarzamy pomiary tak, jak w punktach c) j).
n) Pomiary dla kolejnych próbek wykonujemy zgodnie z punktami a)  m).
Opracowanie wyników
pF
przeliczamy położenia l śruby kondensatora
mm
zmiennego na pojemność Cz w pF. Obliczamy niepewność systematyczną Cz.
Za pomocą stałej aparaturowej A  1,4
a) Na jednym papierze milimetrowym lub wydruku komputerowym sporządzamy
wykresy krzywych rezonansowych dla kondensatora pustego i dla kondensatora z
badanym dielektrykiem w funkcji zmiany pojemności kondensatora zmiennego. W
kilku punktach na wykresie zaznaczamy niepewności pomiarowe.
b) Obliczamy powierzchnię okładek kondensatora płaskiego wiedząc, że średnica
okładki jest równa 95 mm. i dla każdej próbki obliczamy pojemność pustego
kondensatora C0.
c) Obliczamy przenikalność elektryczną badanych płytek. Niepewność pomiarową
wyznaczamy metodą propagacji niepewności pomiarowych.
d) Obliczamy straty dielektryczne i przewodnictwo badanych płytek dielektrycznych
wiedząc, że częstotliwość generatora wynosi 1,2 MHz. Niepewności pomiarowe
wyznaczamy metodą propagacji niepewności pomiarowych.
We wnioskach analizujemy:





o czym świadczy różnica szerokości krzywych rezonansowych dla powietrza i
dla dielektryka i co wynika z porównania kształtów krzywych rezonansowych
badanych substancji.
czy wyznaczone wartości przenikalności elektrycznych i przewodnictwa są w
granicach niepewności pomiarowych zgodne z wartościami tablicowymi.
ile razy przewodnictwo badanych dielektryków jest mniejsze od
przewodnictwa np. miedzi.
który z badanych dielektryków ma najmniejsze przewodnictwo i o czym to
świadczy.
jaki mechanizm powoduje straty dielektryczne.