Budowa histogramu i podstawowe charakterystyki

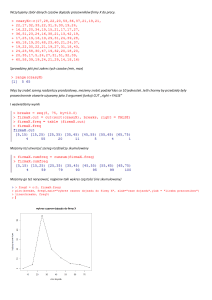
STATYSTYKA MATEMATYCZNA
Budowa histogramu i podstawowe charakterystyki
BUDOWA HISTOGRAMU
Jeżeli liczebność próby dotyczącej jednej cechy mieszanej jest duża
(orientacyjnie 30) to pierwszym etapem opracowania statystycznego jest podział próby na
grupy.
Grupy te noszą nazwę przedziałów klasowych lub krótko klas, a wartością
reprezentującą poszczególne przedziały są ich środki.
Przedziały klasowe oraz liczebność, czyli liczby jednostek próby należących do jednej
klasy, tworzą razem tzw. SZEREG ROZDZIELCZY.
Aby utworzyć szereg rozdzielczy należy:
1. Wyznaczenie
liczb przedziałów klasowych m.
a. liczba przedziałów klasowych nie powinna być mniejsza niż 7 i większa niż 15.
Liczebność w każdym przedziale nie powinna być mniejsza od 5.
b. Sposoby określania :
0.5 n  m  n
m= 1+3.3 log (n)
m  5 log (n)
2. Ustalić obszar zmienności badanej cechy, czyli przedział ograniczony najmniejszym i
największym elementem próby.
R= Xmax-Xmin
3. Podzielić obszar zmienności na klasy i ustalić reprezentację klasy (środek przedziału
klasowego) oraz końce przedziałów klasowych.
Szerokość przedziału klasowego
dd 
X max  X min
m
Wektor brzegów przedziałów Xb
k = 1..m +1
Xbk = Xmin + (k-1) * dd
Wektor środków przedziałów klasowych Xp
j =1..m
Xp j  12 ( Xb j  Xb j 1 )
4. Wyznaczanie liczebności (liczebności, częstości)
f = hist (Xb,X)
5. Wyznaczanie prawdopodobieństwa empirycznego
pj 
fj
n
m - liczba przedziałów
j = 1.. m.
PODSTAWOWE CHARAKTERYSTYKI
1. Wartość średnia:
m
x :
1
n
f
j 1
xp j
j
2. Odchylenie standardowe:
m
s :
f
1
n
j 1
j
(xp j  x ) 2
3. Wariancja:
s2
4. Odchylenie przeciętne:
d :
m
1
n
 xp
j 1
j
x
5. Współczynnik zmienności:
v : xs 100[%]
6. Współczynnik asymetrii:
a :
m
1
ns3
f
j 1
j
(xp j  x ) 3
7. Eksces:
e :
m
1
ns4
f
j 1
j
(xp j  x ) 4  3