Mikroekonomia II 110510-1792 Semestr Letni 2014/2015 - E-SGH

Mikroekonomia II
110510-1792
Semestr Letni 2014/2015
Ćwiczenia 4, 5 & 6
Technologia
1.
Izokwanta produkcji to krzywa obrazująca różne kombinacje nakładu czynników produkcji,
które przynoszą taki sam zysk. P/F
2.
Jeśli występują stałe przychody względem skali, to podwojenie nakładu dowolnego czynnika
produkcji spowoduje podwojenie wielkości produkcji. P/F
3.
a.
b.
c.
Na osobnych wykresach narysuj typową izokwantę dla każdej z następujących funkcji
produkcji.
f(x, y) = min{ 2x, x + y}.
f(x, y) = xy.
f(x, y) = x + min{x, y}.
d.
(x, y) = x +
4.
Które z następujących funkcji produkcji charakteryzowane są przez stałe przychody względem
.
skali? y – product, K i L – czynniki produkcji: (1) y =
. (2) y = 3
. (3) y =
. (4) y = 2K + 3L.
a.
b.
c.
d.
e.
1, 2, i 4
2, 3, i 4
1, 3, i 4
2i3
2i4
Maksymalizacja zysku
1.
Jeśli cena produktu rośnie to wielkość produkcji doskonale konkurencyjnego przedsiębiorstwa
nie może spaść. P/F
2.
Jeśli doskonale konkurencyjne przedsiębiorstwo maksymalizujące zysk ma stałe korzyści skali,
to jego zysk długookresowy musi wynosić 0. P/F
3.
Doskonale konkurencyjna firma maksymalizująca zysk korzysta z jednego czynnika produkcji.
1
Jej funkcja produkcji jest postaci 𝑞 = 4𝑥 2 . Cena produktu wynosi $28 za sztukę, a cena
czynnika produkcji to $7 za sztukę. Ile wynosi popyt na czynnik produkcji?
a. 8.
b. 16.
c. 64.
d. 60.
e. Żadne z powyższych
4.
Doskonale konkurencyjna firma maksymalizująca zysk korzysta z dwóch czynników produkcji.
Jej funkcja produkcji jest postaci 𝑦 = 𝑥1𝑎 𝑥2𝑏 . Cena produktu wynosi 𝑝 za sztukę, a cena
czynników produkcji to 𝑤1 i 𝑤2 . Znajdź wielkości 𝑥1 i 𝑥2 maksymalizujące zysk
przedsiębiorstwa.
5.
Funkcja produkcji jest postaci 𝐹(𝐿) = 6𝐿3 . Koszt zatrudnienia pracy wynosi $16 za jednostkę, a
cena produktu to $16. Ile pracy zatrudni przedsiębiorstwo?
a. 192
2
b.
c.
d.
e.
64
32
128
Żadne z powyższych
Minimalizacja kosztów
1. Jeśli funkcja produkcji charakteryzowana jest przez rosnące korzyści skali, to przeciętny koszt
całkowity maleje wraz z przesuwaniem się w dół po linii jednakowego kosztu. P/F
2. Wynaleziono nowy stop metalu, który składa się z miedzi i cynku. Jedna jednostka nowego
stopa zawiera 4 jednostki cynku i 2 jednostki miedzi. Cena cynku wynosi $2 za jednostkę,
cena miedzy to $5 za jednostkę. Ile wynosi przeciętny koszt całkowity przy wielkości
produkcji 4000 jednostek?
a. $.50
b. $2
c. $18
d. $20
e. $25
1
1
3. Funkcja produkcji jest postaci: 𝑓(𝐿, 𝑀) = 5𝐿2 𝑀2 , gdzie L wielkość zatrudnienia, M liczba
wykorzystanych maszyn. Oba czynniki produkcji są zmienne. Koszt zatrudnienia jednej
jednostki pracy wynosi $9 a koszt wykorzystania jednej maszyny wynosi $64. Jaki jest koszt
całkowity wyprodukowania 12 jednostek produktu
a. $438.
b. $108.
c. $576.
d. $115.20.
e. $57.60.
1
1
4. W krótkim okresie firma korzystająca z funkcji produkcji postaci 𝑓(𝐿, 𝑀) = 4𝐿2 𝑀2 korzysta z
4 maszyn. Cena pracy to $4 za jednostkę, a cena maszyn to $10 za jednostkę. Ile wynosi
krótkookresowy całkowity koszt wyprodukowania 72 jednostek produktu?
a. $504.
b. $288.
c. $720.
d. $728.
e. $364.
5. Przedsiębiorstwo korzysta z dwóch czynników produkcji zgodnie z technologią opisaną przez
funkcję produkcji: 𝑓(𝑥1 , 𝑥2 ) = 𝑥1𝑎 𝑥2𝑏 . Ceny czynników produkcji wynoszą 𝑤1 i 𝑤2 .
𝑥
a.
Znajdź formułę na 𝑥1 przy założeniu produkcji minimalizującej koszty.
2
b.
Znajdź warunkową funkcję popytu na czynniki produkcji oraz funkcję kosztu
całkowitego przy założeniu minimalizacji kosztów produkcji.
Krzywe kosztów
1. Krzywa kosztu krańcowego przecina krzywą przeciętnego kosztu stałego w jego minimum.
P/F
2. Krzywa kosztu krańcowego ma postać MC = 6y. Całkowity koszt zmienny wyprodukowania
10 jednostek produktu wynosi:
a.
b.
c.
d.
e.
$120.
$300.
$80.
$400.
$26.
3. Krzywa kosztu krańcowego ma postać MC = 8y. Całkowity koszt zmienny wyprodukowania
11 jednostek produktu wynosi:
a. $484.
b. $484.
c. $176.
d. $88.
e. $30.
4. Krzywa krótkookresowych kosztów wolnokonkurencyjnej firmy ma postać c(y) = 2y3 – 16y2
+ 128y + 10. W krótkim okresie firma będzie produkować dodatnią wielkość produkcji gdy
cena będzie większa od
a. $192.
b. $48.
c. $99.
d. $96.
e. $95.
1
2
1
2
5. Funkcja produkcji wolnokonkurencyjnego przedsiębiorstwa ma postać y = 8x1 x2. Ceny
czynników produkcji wynoszą p1 = 1 oraz p2 = 4. Nakład obu czynników produkcji jest
zmienny. Koszt krańcowy jest:
a. Stały i równy 0.50.
b. Stały i równy 3.
c. rosnący
d. malejący
e. Żadne z powyższych
6. Funkcja kosztów całkowitych wolnokonkurencyjnego przedsiębiorstwa ma postać c(y)= y3 –
2y2 + 5y + 6. Zapisz postać funkcyjną:
a. przeciętnego kosztu zmiennego
b. kosztu krańcowego
c. przy jakiej wielkości produkcji przeciętny koszt zmienny jest najniższy
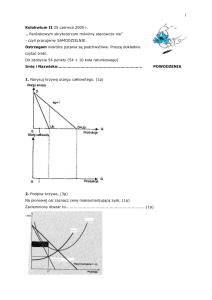
d. narysuj krótkookresową krzywą podaży firmy, zaznacz kluczowe punkty na wykresie.
Podaż firmy
1. Równość ceny i koszt krańcowego to warunek wystarczający maksymalizacji zysku. P/F
2. Funkcja kosztu firmy c(y) = 20y2 + 500 jest U-kształtna. P/F
3. Długookresowa krzywa kosztów firmy jest postaci C(q) = 7q2 + 175. Począwszy od jakiego
poziomu ceny firma będzie dostarczać dodatnią wielkość produkcji na rynek?
a. $70.
b. $148.
c. $35.
d. $140.
e. $75.
1
1
4. Marek sprzedaje gofry w kurorcie górskim. Jego funkcja produkcji jest postaci 𝑦 = 𝑥13 𝑥23 ,
gdzie x1 i x2 to czynniki produkcji. Znajdź funkcję kosztów AC, AVC, MC. Znajdź i narysuj
długookresową krzywą podaży przy stawkach wynagrodzenia czynników produkcji na
poziomie w1=4, w2=9.
Podaż gałęzi
1. Funkcja kosztu całkowitego pewnej firmy będącej cenobiorcą przyjmuje postać 𝑇𝐶 = 3𝑞 3 −
6𝑞 2 + 28𝑞, gdzie q – wielkość produkcji. Krzywa popytu rynkowego na produkty gałęzi, w
której znajduje się firma wynosi Q=190-P. Cena równowagi rynkowej wynosi P=73. Załóżmy,
że struktura kosztów danej formy jest reprezentatywna dla wszystkich firm w gałęzi. Ile firm
będzie funkcjonowało w gałęzi w długim okresie?
Monopol
1. Dla monopolisty, który napotyka opadającą krzywą popytu, przychód krancowy jest mniejszy
od ceny dla dowolnej dodatniej wielkości produkcji. P/F
2. Monopolista napotyka funkcję popytu postaci p = 64 – 2q. Przy jakiej wielkości produkcji
monopolista maksymalizuje swój przychód?
a. 24
b. 26
c. 8
d. 32
e. 16
3. Firma A jest monopolistą na rynku A. Przy obecnej cenie produktu elastyczność cenowa
popytu wynosi –0.50. By maksymalizować zyski firma powinna:
a. Nie zmieniać cen.
b. Zwiększyć wydatki na reklamę.
c. Obniżyć cenę.
d. Podwyższyć cenę
e. Brak wystarczającej ilości informacji.
4. Monopolista napotyka rynkową krzywą popytu postaci D=100-P. Jego krzywa kosztów
krańcowych jest postaci MC=2Q. Oblicz:
a.
Wyznacz funkcję przychodu krańcowego monopolisty oraz narysuj krzywe AR, MR i
MC.
b.
Oblicz ile jednostek produktu będzie produkował monopolista, po jakiej cenie będzie je
sprzedawał na rynku?
c.
Zaznacz na wykresie w punkt A – nadwyżkę konsumenta, nadwyżkę producenta oraz
stratę społeczną. Ile one wynoszą?
Zachowanie monopolistyczne
1. Dyskryminacja cenowa 3. stopnia występuje gdy monopolista sprzedaje produkt różnym
osobom po różnych cenach, ale każda jednostka produktu dla danej osoby kosztuje tyle samo.
P/F
2. Dyskryminujący monopolista jest w stanie różnicować ceny produktu na dwóch różnych
rynkach. Jeśli cena produktu jest taka sama na obu rynkach, to popyt na rynku 1 jest zawsze
większy niż popyt na rynku drugim. W celu maksymalizacji zysku monopolista powinien
żądać wyższej ceny na rynku 1 niż na rynku 2. P/F
3. Monopolista stosujący dyskryminację trzeciego stopnia żąda wyższej ceny za produkt na
rynku charakteryzowanym przez wyższą elastyczność cenową produktu. P/F
4. Monopolista stosuje dyskryminację 3. stopnia na dwóch rynkach. Funkcja popytu na
pierwszym rynku jest postaci: q = 500 – 2p a funkcja popytu na drugim rynku jest postaci q =
1,500 – 6p. By maksymalizować zysk, monopolista powinien:
a. Ustalić wyższą cenę na drugim rynku
b. Ustalić wyższą cenę na pierwszym rynku
c. Ustalić taką samą cenę na obu rynkach
d. Sprzedawać tylko na jednym z dwu rynków
e. Żadne z powyższych
5. Koszt krańcowy, który napotyka monopolista wynosi $2 za sztukę, koszty stałe nie występują.
Monopolista działa na dwóch rynkach, między którymi nie ma interakcji. Ustala cenę p1 na
pierwszym rynku i cenę p2 na drugim rynku. Na pierwszym krzywa popytu na postać: Q1 =
6,000 – 600p1 a na drugim Q2 = 2,400 – 400p2, wówczas cena na pierwszym będzie
a. Większa niż na drugim o 2
b. Mniejsza niż na drugim o 2.
c. Taka sama na obu rynkach
d. Większa niż cena na drugim rynku o $4.
e. Mniejsza niż cena na drugim rynku o $4
6. Koszt krańcowy, który napotyka monopolista wynosi $2 za sztukę, koszty stałe nie występują.
Monopolista działa na dwóch rynkach, między którymi nie ma interakcji. Ustala cenę p1 na
pierwszym rynku i cenę p2 na drugim rynku. Na pierwszym krzywa popytu na postać: Q1 =
7,000 – 700p1 a na drugim Q2 = 3,200 – 400p2, wówczas cena na pierwszym będzie
a. Mniejsza niż na drugim o 1.
b. Większa niż na drugim o 3.
c. Taka sama na obu rynkach
d. Większa niż na drugim o 1.
e. Mniejsza niż na drugim o 3.
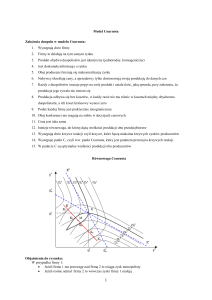
Oligopol
1. Na rynku oligopolistycznym produkują dwie firmy napotykając popyt rynkowy opisany
wzorem: P = 200-Q, gdzie P to cena jednostki produktu a Q to wielkość sprzedaży. Każdy z
konkurentów ponosi stałe koszty krańcowe równe 50.
a.
Oblicz q1, q2, Q i P w równowadze Cournota
b.
Firma 1 przyjęła rolę lidera. oblicz q1, q2, Q i P w równowadze Stackelberga
c.
Firmy dogadują się i wspólnie maksymalizują zysk całego rynku zachowując się jak
monopolista. Oblicz q1, q2, Q i P.
d.
Firmy działają jak w konkurencji doskonałej. Oblicz q1, q2, Q i P.
2. Odwrócona funkcja popytu na ryż jest postaci p = 20 – q. W gałęzi występują stałe efekty
skali a koszty jednostkowe produkcji wynoszą 8. Które ze stwierdzeń jest w całości
prawdziwe?
a. Produkcja monopolu wynosi 6. Równowaga w modelu Cournota wynosi 8, a lider w
modelu Stackelberga produkuje 8.
b. Produkcja monopolu wynosi 8. Równowaga w modelu Cournota wynosi 8, a lider w
modelu Stackelberga produkuje 8.
c. Produkcja monopolu wynosi 6. Równowaga w modelu Cournota wynosi 6, a naśladowca
w modelu Stackelberga produkuje 3.
d. Produkcja monopolu wynosi 6. Równowaga w modelu Cournota wynosi 8, a naśladowca
w modelu Stackelberga produkuje 3.
e. Produkcja monopolu wynosi 6. Równowaga w modelu Cournota wynosi 8, a naśladowca
w modelu Stackelberga produkuje 4.
Teoria gier
1. Zad.
Wisła Kraków
a.
b.
Góra
Dół
Lewo
(6,5)
(2,3)
Lech Poznań
Prawo
(4,7)
(0,4)
Wskaż strategię dominującą dla Wisły Kraków, wskaż strategię dominującą dla Lecha Poznań.
Wyznacz równowagę Nasha. Odpowiedź uzasadnij.
2. Zad.
Jagiellonia Białystok
a.
b.
c.
Góra
Dół
Lewo
(7,5)
(6,12)
Górnik Zabrze
Prawo
(10,4)
(11,13)
Wskaż strategię dominującą dla Jagiellonii Białystok, wskaż strategię dominującą dla Górnika
Zabrze.
Wyznacz równowagę Nasha. Odpowiedź uzasadnij.
Wyjaśnij dlaczego para strategii (dół, lewo) nie jest równowagą Nasha.
3. Zad. Dylemat więźnia
Macierz wypłat (poziom zysku w zależności od przestrzegania postanowień współpracy) dwóch
przedsiębiorstw kształtuje się następująco:
Firma A
a.
b.
c.
oszustwo
przestrzeganie
oszustwo
(0,0)
(-1;4,5)
Firma B
przestrzeganie
(4,5;-1)
(2,2)
Wskaż strategię dominującą dla każdej z firm.
Wyznacz równowagę Nasha. Odpowiedź uzasadnij.
Wyjaśnij dlaczego para strategii (przestrzeganie, przestrzeganie) nie jest równowagą Nasha.