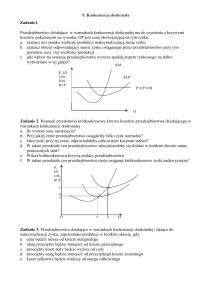
Przedsiębiorstwo jako oferent dóbr
Przedsiębiorstwem będziemy nazywali organizację, która odpłatnie
dostarcza innym podmiotom dobra i czyni to zgodnie z
ustawodawstwem danego kraju.
Dlaczego przedsiębiorstwa musiały powstać?
Dlaczego przedsiębiorstwa uzyskały osobowość prawną?
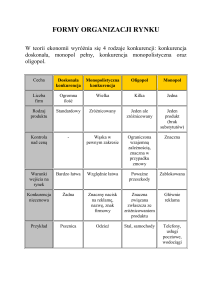
Klasyfikacje przedsiębiorstw
Przedsiębiorca – właściciel firmy lub osoby przez niego
upoważnione do kierowania przedsiębiorstwem - menedżerowie
Klasyfikacje czynników produkcji
Wszystkie dobra materialne i niematerialne, które są niezbędne do
prowadzenia działalności gospodarczej nazywamy czynnikami
produkcji.
Przykłady czynników produkcji.
Klasyfikacja 1.
• kapitał rzeczowy,
• kapitał ludzki (praca)
• zasoby naturalne (ziemia)
Klasyfikacja 2.
• stałe czynniki produkcji,
• zmienne czynniki produkcji.
Kryterium podziału jest to, czy ilość danego czynnika produkcji w
typowych warunkach zmienia się w danym okresie czasu wraz ze
zmianą wielkości produkcji, czy też nie.
Jeżeli przedsiębiorca prowadzi analizę ekonomiczną dla danego okresu
i stwierdza, że wielkość produkcji będzie się zmieniać, to czy w
typowych warunkach będzie skłonny zmieniać ilość danego czynnika
produkcji?
Tym kryterium nie jest zmienność czynnika produkcji w czasie.
Przykłady klasyfikacji.
Im dłuższy okres analizy, tym większa część stałych czynników
produkcji staje się zmiennymi czynnikami produkcji.
Koszty produkcji
Definicja kosztów produkcji
koszty
księgowe
inne wydatki
nie uznane
jako koszty
księgowe
koszty
alternatywne
koszty
ekonomiczne
koszty
zewnętrzne
koszty
społeczne
Analiza krótko i długookresowa
Analiza długookresowa obejmuje taki przedział czasu, w którym
wszystkie czynniki produkcji stają się zmiennymi czynnikami
produkcji.
Analiza krótkookresowa obejmuje taki przedział czasu, w którym
występują stałe czynniki produkcji.
Względny charakter tego podziału.
Stałe i zmienne koszty
Koszty stałe to takie, których zmiany wysokości, w danym okresie,
nie zależą od zmian wielkości produkcji.
Koszty zmienne to takie, których zmiany wysokości, w danym
okresie, zależą od zmian wielkości produkcji.
W większości przypadków zużycie stałego czynnika produkcji
oznacza powstanie kosztu stałego.
Zużycie zmiennego czynnika produkcji oznacza powstanie kosztu
zmiennego.
Koszty całkowite
Przeciętne koszty całkowite
Przeciętne koszty zmienne
Przeciętne koszty stałe
Koszty krańcowe (marginalne)
Kc = Kz + Ks
Kc
K cp
y
Kz
K zp
y
Ks
K sp
y
Kc
Kc '
y
dK c
Kc'
dy
Rozpatrzmy przypadek:
Koszty stałe wynosza 1000 zł,
Przeciętne koszty zmienne wynoszą 10 zł/szt. i nie zależą od zmian
wielkości produkcji.
y
Kz
0
1
2
3
4
5
100
1000
100000
Kc
Kcp
Ksp
Kc’
y
Kz
Kc
0
1
2
0
10
20
3
4
5
30
40
50
100
1000
100000
1000
10000
1000000
Kcp
Ksp
Kc’
y
Kz
0
1
2
0
10
20
Kc
1000
1010
1020
3
4
5
30
40
50
1030
1040
1050
100
1000
100000
1000
10000
1000000
2000
11000
1001000
Kcp
Ksp
Kc’
y
Kz
0
1
2
0
10
20
Kc
1000
1010
1020
Kcp
1010
510
3
4
5
30
40
50
1030
1040
1050
343,33
260
210
100
1000
100000
1000
10000
1000000
2000
11000
1001000
20
11
10,01
Ksp
Kc’
y
Kz
0
1
2
0
10
20
Kc
1000
1010
1020
Kcp
1010
510
Ksp
1000
500
3
4
5
30
40
50
1030
1040
1050
343,33
260
210
333,33
250
200
100
1000
100000
1000
10000
1000000
2000
11000
1001000
20
11
10,01
10
1
0,01
Kc’
y
Kz
Kcp
1010
510
Ksp
1000
500
Kc’
-
0
1
2
0
10
20
Kc
1000
1010
1020
3
4
5
30
40
50
1030
1040
1050
343,33
260
210
333,33
250
200
10
10
10
100
1000
100000
1000
10000
1000000
2000
11000
1001000
20
11
10,01
10
1
0,01
10
10
10
10
10
Na jakie zmiany są wrażliwe Kcp i Kzp?
Kc K z K s
Kc K z K s
/: y
K cp K zp K sp
Koszty krańcowe
Koszty krańcowe pokazują o ile zmienią się koszty całkowite, gdy
zmienimy wielkość produkcji o jednostkę.
Z tego nie wynika, że koszt krańcowy pokazuje koszt wytworzenia
danej jednostki produkcji.
Aby to pokazać dokonajmy przekształceń:
Kc K z K s
K c ' K z ' K s '
K z
Kc ' K z '
y
K s ' 0
Koszty krańcowe są pochodną funkcji kosztów całkowitych i
zmiennych. Tym samym pokazują nachylenie obu tych funkcji.
Przebieg funkcji kosztów
Funkcje kosztów całkowitych i zmiennych
Zacznijmy od przedstawienia przypadku przedstawionego w tabeli.
Kz
Kc
1000
tg = 10
y
Typowy przebieg funkcji kosztów całkowitych i zmiennych
Kz
Kc
y
Kc
G
A
0
yA
yG
F C
yF yC
Kcp
y
Kc’
Kcp
Kzp
yG
yF yC
y
Zależności, które należy przestrzegać przy rysowaniu typowego
przebiegu funkcji Kcp, Kzp, Kc’.
1. Funkcja Kcp nie może przecinać pionowej osi układu
współrzędnych.
2. Jeżeli koszty stałe są większe od 0, to funkcja Kzp musi leżeć
poniżej Kcp ale Kzp może dochodzić do pionowej osi układu
współrzędnych.
3. Minimum funkcji Kzp musi leżeć na lewo w dół od minimum Kcp.
4. Funkcja Kc’ dla y dążącego do 0 zaczyna się z tego samego
miejsca jak funkcja Kzp.
5. Funkcja Kc’ przecina funkcje Kzp , Kcp w ich minimach.