Prąd i opór elektryczny
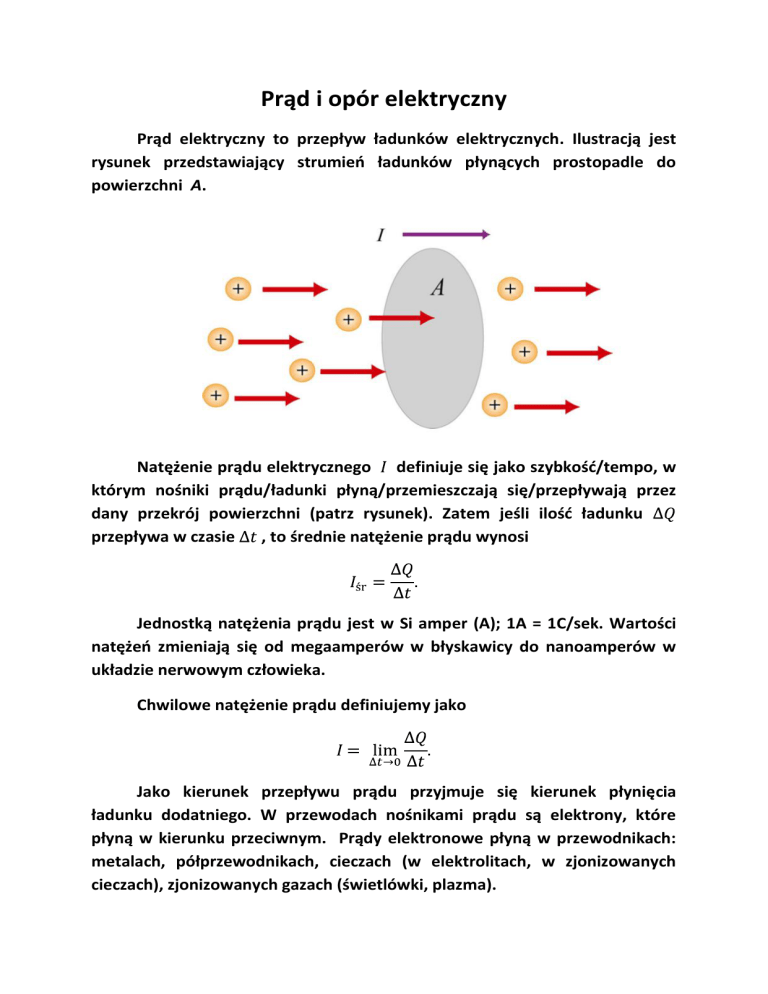
Prąd elektryczny to przepływ ładunków elektrycznych. Ilustracją jest
rysunek przedstawiający strumieo ładunków płynących prostopadle do
powierzchni A.
Natężenie prądu elektrycznego definiuje się jako szybkośd/tempo, w
którym nośniki prądu/ładunki płyną/przemieszczają się/przepływają przez
dany przekrój powierzchni (patrz rysunek). Zatem jeśli ilośd ładunku
przepływa w czasie , to średnie natężenie prądu wynosi
Jednostką natężenia prądu jest w Si amper (A); 1A = 1C/sek. Wartości
natężeo zmieniają się od megaamperów w błyskawicy do nanoamperów w
układzie nerwowym człowieka.
Chwilowe natężenie prądu definiujemy jako
Jako kierunek przepływu prądu przyjmuje się kierunek płynięcia
ładunku dodatniego. W przewodach nośnikami prądu są elektrony, które
płyną w kierunku przeciwnym. Prądy elektronowe płyną w przewodnikach:
metalach, półprzewodnikach, cieczach (w elektrolitach, w zjonizowanych
cieczach), zjonizowanych gazach (świetlówki, plazma).
Wektor gęstości prądu
W celu powiązania prądu elektrycznego z mikroskopowymi
wielkościami (ładunkiem nośników prądu) rozpatrzymy przewodnik o polu
przekroju poprzecznego A (patrz rysunek)
Przedstawimy teraz prąd elektryczny (przepływ ładunków) jako
strumieo nowego wektora przez powierzchnię A
,
gdzie jest wektorem gęstości prądu elektrycznego. Jego wymiarem w
Si jest A/m2.
Niechaj ładunek nośnika prądu wynosi , koncentracja nośników ,
wtedy całkowity ładunek płynący w objętości przewodnika pokazanej na
rysunku wyniesie
Załóżmy, że prędkośd nośników prądu jest równa
ładunki przebędą drogę
. Wtedy w czasie
Całkowite średnie natężenie prądu, który w tym czasie płynął przez
przewodnik jest równe
Prędkośd
, z jaką nośniki prądu „płyną” w przewodniku przyjęto
nazywad prędkością dryfu (prędkośd dryfowania, prędkośd unoszenia przez
pole elektryczne).
Z fizycznego punktu widzenia prędkośd
jest średnią prędkością
nośników prądu w objętości przewodnika, gdy w przewodniku istnieje pole
elektryczne (tak jest po podłączeniu przewodnika do źródła prądu).
Zauważmy, że w objętości przewodnika nośniki prądu nie poruszają się po
liniach prostych lecz wykonują pewnego rodzaju błądzenie losowe, co
ilustruje kolejny rysunek.
W metalach dzieje się tak wskutek zderzania się prawie swobodnych
elektronów gazu elektronowego z jądrami atomów metalu.
Zestawienie dwóch ostatnich wzorów prowadzi nas do ważnego
wyrażenia dla wektora gęstości prądu elektrycznego. Zauważmy, że
zatem
Jeśli teraz założymy, że wszystkie nośniki prądu mają identyczne
wektory dryfu a wektor gęstości prądu jest stały w każdym punkcie pola
przekroju poprzecznego przewodnika, to
Jak widzimy wektor ma ten sam kierunek i zwrot co wektor prędkości
dryfu
nośników prądu!
Jak wyznaczamy średnią wartośd dryfu nośników prądu?
Odnotujmy, że na elektron umieszczony w polu elektrycznym działa siła
,
gdzie położono, że
Niechaj prędkośd danego elektronu tuż po zderzeniu z innym lub
jadrem atomowym wynosi . Wtedy prędkośd elektronu tuż przed kolejnym
zderzeniem wyniesie
.
Prędkośd średnia elektronu w czasie między zderzeniami, czyli prędkośc
dryfu jest równa
Pod nieobecnośd pola elektrycznego
, więc
Niechaj średni czas
gęstości prądu elektrycznego
między zderzeniami wynosi . Wtedy wektor
Zauważmy, że wektory oraz
mają te same kierunki i zwroty.
Prawo Ohma
W wielu przypadkach, tak jest w metalach, wektor gęstości prądu jest
proporcjonalny do natężenie pola elektrycznego, które oddziaływuje na
nośniki prądu elektrycznego znajdujące się w objętości przewodnika.
Zapisujemy to w postaci
gdzie
nosi nazwę przewodności materiału przewodnika. W Si
jednostką przewodnictwa jest simens, przy czym 1S = (A/m2)/(N/C) =
(A/m2)/(V/m) = A/(mV).
Powyższe równanie nosi nazwę mikroskopowego prawa Ohma.
Materiał spełniający to prawo nazywamy opornikiem ohmowym.
Porównując dwa ostatnie wzory dochodzimy do związku
Wyprowadzimy obecnie inna tzw. całkową postad prawa Ohma dla
prostoliniowego przewodnika o długości , polu przekroju poprzecznego ,
co pokazuje rysunek.
Załóżmy, że różnica potencjałów
dzieli kooce
przewodnika, co generuje pole elektryczne w przewodniku o natężeniu i
przepływ prądu o natężeniu Jeśli pole jest jednorodne, to
.
Wartośd wektora gęstości prądu elektrycznego wynosi
co po prostym przekształceniu pozwala otrzymad
gdzie
jest oporem prostoliniowego przewodnika z prądem.
Makroskopowe równanie Ohma zapisujemy w postaci
W układzie SI jednostką oporu elektrycznego
jest Ohm (), przy czym
1 = 1V/(1A). Materiał spełniający ostatnie z podanych wyżej równao
nosi nazwę ohmowego. Tuta rozpatrujemy tylko takie materiały. W tej klasie
znajdują się metale. Kolejny rysunek przedstawia materiał ohmowy i
nieohmowy (po prawej stronie)
Opornośd właściwą
Zwiążemy obecnie
definiujemy jako odwrotnośd przewodnictwa
z oporem R.
i ostatecznie opór prostoliniowego przewodnika z prądem jest równy
.
Warto dodad, że opornośd właściwa
zależy od temperatury
materiałów ohmowych
,
gdzie
elektrycznego.
jest
temperaturowym
współczynnikiem
oporu
Tabela przedstawia typowe wartości wprowadzonych do tej pory
wielkości.
Legenda: Tungsten – wolfram, Iron – żelazo, Alloys – stopy, Brass – mosiądz, Manganin stop miedzi z manganem i niklem, Nichrome – niemagnetyczny stop niklu I chromu (80%
niklu i 20% chromu), Carbon (grafit) – forma/faza grafitowa węgla, Glass – szkło, Sulfur –
siarka, Quartz – kwarc, Germanium – german, Silicon – krzem, Semiconductors –
półprzewodniki, Insulators – izolatory, Elements – pierwiastki.
Praca i moc prądu elektrycznego
Rozpatrzmy zamknięty układ elektryczny przedstawiony na rysunku.
Układ zawiera opór . Napięcie między okładkami baterii wynosi
. Niech ładunek
zostanie przemieszczony przez baterię, to jego
energia wzrośnie o
. Z drugiej strony ten sam ładunek płynący
przez opornik w obwodzie traci swoją energię wskutek zderzeo z atomami
opornika. Jeśli zaniedbamy oporności baterii i przewodów łączących, to
płynący ładunek nie traci dodatkowo energii. Zatem strata energii ładunku
wynosi
Otrzymany wzór określa także moc dostarczaną obwodowi przez baterię!
Stały prąd elektryczny
Obwód elektryczny łączy, za pomocą przewodów elektrycznych, źródło
prądu elektrycznego z tzw. obciążeniem, którym mogą byd: rezystory
(oporniki), silniki, grzejniki, lampy. Energia elektryczna płynie natychmiast po
uruchomieniu włącznika (włączenie kontaktu).
Elementy obciążenia mogą byd połączone równolegle (lewa częśd
rysunku) lub szeregowo.
Poniżej pokazujemy schematyczne oznaczenia elementów obwodów
elektrycznych
Legenda: Voltage Source – źródło napięcia, resistor – opornik (rezystor), Switch –
przełącznik (kontakt).
Odnotujmy, że tzw. uziemienie, to element lub punkt obwodu
elektrycznego, którego potencjał jest umownie przyjmowany jako zerowy.
Potencjał
dowolnego punktu obwodu jest liczony (odnoszony) do
potencjału uziemionego elementu.
Siła elektromedyczna (SEM=EMF)
Źródło energii np. bateria, akumulator, generator, komórka
fotowoltaiczna płynącej w każdym obwodzie elektrycznym nazywane jest
źródłem siły elektromotorycznej SEM. Możemy o źródle tej energii jako o
pompie ładunków, która powoduje przemieszczanie się ładunków
elektrycznych z punktu o mniejszym potencjale do punktu o potencjale
wyższym. Przypomnijmy, że prąd elektryczny płynie od punktów o wyższym
potencjale do punktów o potencjale niższym.
Wartośd siły elektromotorycznej, oznaczanej symbolem , definiuje się
za pomocą wzoru
.
Powyższe wyrażenie oznacza więc pracę konieczną do przeniesienia
jednostkowego ładunku w kierunku rosnącego potencjału.
W SI jednostką siły elektromotorycznej jest wolt (V).
Rozpatrzymy teraz obwód elektryczny przedstawiony na kolejnym
rysunku
Załóżmy najpierw, że bateria ma zerowy opór wewnętrzny oraz, że
różnica potencjałów między dodatnim i ujemnym jej zaciskiem jest równa
Oznacza to, że
.
Uruchomienie przepływu prądu w obwodzie elektrycznym jest
wynikiem procesu zamiany energii chemicznej na elektryczną. Zauważmy, że
SEM to ilośd energii chemicznej potrzebnej do uwolnienia jednostkowego
ładunku elektrycznego. Proces ten zachodzi w baterii.
Ze względu na zachowawczy charakter pola elektrostatycznego praca W
potrzebna do przemieszczenia ładunku
po krzywej zamkniętej, tj. po
obwodzie zamkniętym wynosi zero
Rozważmy pkt. a na poniższym rysunku.
Obchodzimy obwód zamknięty zgodnie z ruchem wskazówek zegara
zaczynając od punktu a. Przejście przez SEM oznacza wzrost potencjału o
wartośd . Przejście przez rezystor oznacza spadek napięcia równy . Jeśli
opory przewodników i opór wewnętrzny zaniedbamy, to
zatem
.
W rzeczywistości bateria ma niezerowy opór elektryczny, więc
rzeczywisty obwód ma postad
Na tej podstawie możemy przedstawid (patrz poniżej) graficznie spadek
napięcia w powyższym obwodzie
Zauważmy, że najwyższy potencjał ma w obwodzie dodatni zacisk
baterii.
Różnica potencjałów
na zaciskach baterii jest teraz równa
Ponieważ pole jest zachowawcze, więc otrzymujemy prawo Ohma dla
układu zamkniętego
i
.
Moc prądu w obwodzie zamkniętym wynosi
Baterie oporników
Połączenie szeregowe – dwóch oporników tworzących najmniejszą z
możliwych baterię przedstawia poniższy rysunek; po jego prawej stronie
opornik zastępczy (ekwiwalentny)
Spadek napięcia między punktami a i c obwodu
.
Układ 2 rezystorów można zastąpid w obwodzie jednym opornikiem
którym spadek napięcia jest
.
Porównanie dwóch ostatnich wzorów
, na
,
prowadzi nas do wniosku o dodawaniu się oporów połączonych
szeregowo, tj.
W ogólnym przypadku takie same rozważania dają wynik koocowy na opór
zastępczy baterii N oporów połączonych szeregowo
Połączenie równoległe – dwóch oporników tworzących najmniejszą z
możliwych baterię przedstawia poniższy rysunek; po jego prawej stronie
opornik zastępczy (ekwiwalentny)
Z prawa zachowania ładunku elektrycznego wynika, że w punkcie a
obwodu natężenie prądu I dzieli się na prądy oraz płynące odpowiednio
przez oraz
, czyli
.
Oporniki są ohmowe więc spadki napięd na nich są równe
oraz
,
co pozwala zapisad, z uwzględnieniem równości spadków napięd na
każdym z oporników, kolejną równośd
,
co oznacza, że
.
Tak więc przy równoległym połączeniu 2 rezystorów w jedną baterię
oporników, jej równoważną (zastępcza) opornośd liczymy zgodnie z ostatnim
wzorem.
W ogólnym przypadku takie same rozważania dają wynik koocowy na
opór zastępczy baterii N oporów połączonych równolegle
Prawa Kirchhoffa
Pierwsze prawo Kirchhoffa: Suma natężeo wpływających do danego węzła
obwodu jest równa sumie natężeo prądów wypływających z niego
.
W ostatnim wzorze przyjęto, że do węzła obwodu wpływa
prądów
(natężeo) oraz
wypływa; w ogólności
Prostą sytuację przedstawia
poniższy rysunek
gdzie
oraz
Drugie prawo Kirchhoffa: Suma spadków napięd w zamkniętym oczku
obwodu elektrycznego jest równa zeru
.
(*)
Reguły znaków obowiązujące dla składników powyższej sumy zawiera
poniższa tabela
Komentarze:
1. Aby zastosowad II prawo Kirchhoffa wybieramy kierunek
obchodzenia zamkniętego oczka. W tabeli wybrano kierunek
obchodzenia zgodny z ruchem wskazówek zegara. Przyjęcie
przeciwnego kierunku obchodu nie zmienia wyników koocowych.
Dlaczego?
2. Jeśli „przechodząc” przez opornik z prądem wstępnie wybrany
kierunek przepływu prądu jest zgodny z kierunkiem obchodzenia
oczka, to spadek potencjału (napięcia) równy
bierzemy
do wyżej przytoczonej sumy ze znakiem ujemnym. W przeciwnym
przypadku ze znakiem dodatnim; patrz górny wiersz tabeli.
3. Jeśli „obchodząc” oczko przy wybranym kierunku obchodzenia
natrafiamy na zacisk ujemny (niższy potencjał) źródła prądu, to
spadek napięcia
, tj. siłę elektromotoryczną źródła
bierzemy, do sumy ze znakiem dodatnim. W przeciwnym
przypadku ze znakiem ujemnym; patrz dolny wiersz tabeli.
Regułę drugą oraz drugi komentarz, którym odpowiada lewy górny róg
tabeli łatwo zapamiętad i zrozumied. Prąd elektryczny płynie od miejsc o
wyższym potencjale do miejsc o mniejszym potencjale. „Przechodząc” w
obchodzie oczka opornik (kierunek obchodzenia i kierunek przepływu prądu
są zgodne) zauważamy, że różnica potencjałów między jego koocem i
początkiem jest ujemna; dlatego spadek napięcia ma wartośd ujemną, tj.
; oznacza to, że
. Dlatego do sumy (*)
spadek napięcie wpisujemy ze znakiem ujemnym. Jeśli jednak kierunek
obchodu oczka i kierunek prądu w oporniku są przeciwne (patrz prawy górny
róg tabeli), to spadek napięcia ma wartośd dodatnią, tj.
. Obowiązuje
tutaj zasada podwójnego minusa. Otóż przyjmując kierunek przepływu prądu
w lewo (patrz prawy górny róg tabeli) uważamy, że potencjał punktu a jest
niższy niż punktu b. Zatem
Ale kierunek obchodu
jest przeciwny do kierunku prądu. Dlatego spadek napięcia na w tym
przypadku wyniesie
Oznacza to
więc, że do sumy (*) spadek napięcie wpisujemy ze znakiem dodatnim.
Regułę drugą oraz trzeci komentarz jest również stosunkowo łatwo
zrozumied i zapamiętad. „Obchodząc” oczko i przechodząc przez źródło prądu
zgodnie z wybranym kierunkiem obchodzenia od bieguna ujemnego do
dodatniego (patrz lewy dolny róg tabeli) wartośd SEM wpisujemy do sumy (*)
ze znakiem dodatnim. Wędrówka ładunku dodatniego od ujemnego do
dodatniego zacisku oznacza przejście od miejsca o potencjale niższym do
miejsca o potencjale wyższym. Wtedy zamiast spadku potencjału mamy jego
wzrost równy
. Jeśli jednak obchodząc oczko
zgodnie z przyjętym kierunkiem przechodzimy przez źródło w ten sposób, że
najpierw natrafiamy na dodatni biegun źródła (patrz dolny prawy ród tabeli),
to
. Dlatego w tym przypadku do sumy (*)
SEM wpisujemy ze znakiem ujemnym.
Przykład przedstawia poniższy rysunek, na którym widzimy układ zwany
dzielnikiem napięcia.
Napięcie na wyjściu
napięcia na wejściu
otrzymujemy
, tj. spadek napięcia na oporniku
jest mniejszy od
. Stosując II prawo Kirchhoffa do zamkniętego oczka
,
więc
,
a szukane napięcie
na wyjściu dzielnika jest równe
,
tj.
W ostatnim wzorze przyjęto, że do węzła obwodu wpływa
prądów
(natężeo) oraz
wypływa; w ogólności
Prostą sytuację przedstawia
poniższy rysunek
gdzie
oraz
Strategia rozwiązywania zadao z wykorzystaniem praw Kirchhoffa
1.
Narysuj schemat układu elektrycznego. Wskaż i nanieś na rysunek
wielkości znane i nieznane. Liczba niewiadomych powinna byd równa liczbie
niezależnych równao.
2.
Przypisz/przyporządkuj
każdemu oczku w analizowanym
obwodzie kierunek obchodzenie. Jeśli wybierzesz kierunek obchodzenia
niezgodnie z rzeczywistym płynięciem prądu, to otrzymasz wartości ujemne
wyznaczanych niewiadomych.
3.
Zastosuje I regułę Kirchhoffa do węzłów układu.
4.
Zastosuj II i III regułę Kirchhoffa do zamkniętych oczek w
układzie. Pozwoli to na sformułowanie odpowiedniej liczby niezależnych
równao (patrz pkt. 1). Przestrzegaj przy tym następujących reguł znaków:
5.
Rozwiąż otrzymany układ równao liniowych.
Przykład. W poniższym układzie
znane są ,
oraz opory
prądów , oraz .
,
i
Mamy wyznaczyd natężenia
1. Opatrzony
Rozwiązanie
symbolami schemat układu
elektrycznego
jest
przedstawiony poniżej.
Niewiadomymi są natężenia prądów ,
2.
oraz .
Na rysunku przyporządkowano
każdemu z dwóch oczku
kierunek obchodzenie.
3.
Stosujemy I regułę Kirchhoffa do węzła b i otrzymujemy
.
4.
Stosujemy II i III regułę Kirchhoffa do zamkniętych oczek 1 i 2 w
analizowanym układzie. Pozwala to nam sformułowad dwa dodatkowe
niezależne równania. Przestrzegamy podanych wyżej reguł znaków. Dla oczka
befcb
Podobnie dla oczka abcda otrzymujemy
5. Rozwiązujemy układ 3 równao liniowych i wyznaczamy szukane
natężenia prądu
,
Obwód RC prądu stałego
Ładowanie kondensatora
Rozpatrzymy obecnie proces ładowania kondensatora umieszczonego
w obwodzie pokazanym na rysunku
Po zwarciu klucza (rys. prawy) w układzie płynie prąd. Mówimy, że
następuje ładowanie kondensatora. W chwili początkowej, kondensator nie
jest naładowany, więc początkowa wartośd prądu wyniesie
.
W chwilę potem napięcie na kondensatorze, początkowo równe zeru
zaczyna narastad i w chwili t wyniesie
Zastosujemy teraz reguły Kirchhoffa do obwodu zamkniętego
pokazanego na prawym rysunku. W poniższej tabeli zamieszczono znaki
spadków napięd na kondensatorze umieszczonym w obwodzie prądu stałego.
Lewa kolumna pokazuje, że przechodzenie przez kondensator oznacza wzrost
lub spadek potencjału liczony tak, jakby był on źródłem prądu (bo jest).
Zauważmy, że podczas ładowania kondensatora rośnie napięcie między
jego okładkami, aż osiągnie po pewnym czasie wartośd SEM, tj. . Od tego
momentu natężenie prądu jest równe zeru.
Dynamikę ładowania, czyli zależnośd
oraz
wyznaczymy
rozwiązując „równanie ruchu”, tj. równanie różniczkowe o postaci
.
Po rozseparowaniu zmiennych mamy
którego scałkowanie
pozwala napisad
Z ostatniego wyrażenia otrzymujemy ostatecznie
,
gdzie
jest maksymalnym ładunkiem zgromadzonym na
kondensatorze. Wyprowadzona zależnośd graficznie ilustruje kolejny rysunek
Z rysunku widad, że maksymalny ładunek zostanie zgromadzony na
kondensatorze po czasie równym nieskooczoności. Podobnie ma się sprawa z
potencjałem kondensatora, którego zależnośd o d czasu zadaje równanie
.
Natężenie prądu w układzie podczas ładowania kondensatora także
zależy od czasu
Poniżej graficzna ilustracja ostatniego związku
Często wprowadza się pojęcie stałej czasowej obwodu RC, która jest
równa
Wtedy
Jaki jest wymiar stałej czasowej obwodu?
Dla
mamy
(patrz rysunek poniżej)
Zauważmy, że po czasie
wartośd
napięcie na okładkach kondensatora osiąga
Rozładowanie kondensatora
Rozpatrzymy obecnie proces odwrotny do ładowania, czyli rozładowania
kondensatora umieszczonego w obwodzie pokazanym na rysunku
Przed zwarciem klucza (rys. lewy) w układzie nie płynie prąd. Mówimy,
że kondensator jest naładowany. Po zwarciu klucza (rys. prawy) kondensator
zaczyna rozładowywad się poprzez opornik. Początkowa wartośd napięcia na
koocówkach oporu wynosi
Po zainicjowaniu rozładowywania
kondensator działa w rozpatrywanym obwodzie jak źródło prądu. Stosując
reguły Kirchhoffa otrzymujemy teraz (patrz rys. prawy)
.
Prąd płynący w obwodzie
gdzie użyto znak minus w celu wskazania tego, że szybkośd zmiany
ładunku jest proporcjonalna do ujemnej wartości ładunku zgromadzonego na
kondensatorze. Zauważmy, że ładunek na okładce dodatniej maleje! Zatem
równanie ruchu teraz przyjmuje postad równania różniczkowego
Po rozseparowaniu zmiennych otrzymujemy równanie
które jest łatwo całkowalne
co po odwróceniu funkcji logarytmicznej prowadzi do równania na
zależnośd ładunku zgromadzonego na rozładowywanym kondensatorze
.
Napięcie na kondensatorze zależy również od czasu
.
Ilustracją graficzną ostatniej zależności jest
.
Zauważmy, że również natężenie prądu w rozpatrywanym obwodzie
maleje wraz z czasem jak
Wyprowadzoną zależnośd graficznie ilustruje kolejny rysunek
Z rysunku widad, że natężenie prądu w obwodzie maleje do wartości
po czasie równym stałej czasowej obwodu RC