Temat: Zadania początkowe z fizyki

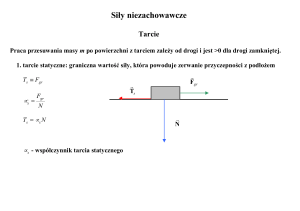
Temat: Zadania początkowe z fizyki
Zadao nie będzie tu dużo ale będą wyselekcjonowane bardzo…
Zadanie 1
(wg Jędrzejewski, Kruczek, Kujawski)
Kierowca jadący z prędkością v zobaczył nagle przede sobą przeszkodę.
Aby uniknąć wypadku powinien zahamować czy zakręcić o 90 stopni?
Rozwiązanie
Załóżmy, że jest dany współczynnik tarcia µ (oraz masa pojazdu m)
Siła tarcia w obu przypadkach wynosi: Ft =
gdzie Q jest siłą nacisku czyli ciężarem:
µQ
Q = mg (g jest ziemskim przyspieszeniem grawitacyjnym,
zawsze uważanym za dane)
Też w obu przypadkach mamy do czynienia z przyspieszeniem a;
Przy hamowaniu jest to opóźnienie ruchu jednostajnie (ogólnie) przyspieszonego i
przyspieszenie to pomnożone przez masę (II zasada Dynamiki Newtona) musi byd wspomnianą siłą
tarcia aby nie było poślizgu:
F = am
µmg = am
czyli a
= µg
Z takim przyspieszeniem (ujemnym czyli: opóźnieniem) samochód przebędzie drogę: s
Czas t wyznaczymy ze wzoru definiującego przyspieszenie: a
t=
s=
=
𝜈
𝑡
=
𝑎𝑡 2
2
gdzie v jest oczywiście szybkością
𝜈
𝑎
𝑎
𝜈
2
𝑎
2
=
𝜈2
2𝑎
s=
𝜈2
2µg
Przy skręcaniu przyspieszenie jest dośrodkowym a =
(minimalnym aby nie było poślizgu) o 90o
Stąd R
=
𝜈2
𝑎
𝜈2
𝑅
gdzie R jest promieniem skrętu
R=
𝜈2
µ𝑔
Czyli R = 2S
Bezpieczniej jest hamowad!
Zadanie 2
(wg Jędrzejewski, Kruczek, Kujawski)
Pojazd poruszać się może (zsuwać) po torze wypukłym albo wklęsłym
(części okręgu o tym samym promieniu). Kiedy będzie nań działać większa
siła tarcia?
Rozwiązanie
Załóżmy, że jest dany współczynnik tarcia, masa, promieo krzywizny, prędkośd.
W przypadku wklęsłego toru nacisk będzie większy o siłę odśrodkową a w przypadku wypukłego –
mniejszy. Siła tarcia od nacisku zależy (wprost)proporcjonalnie więc
większa siła tarcia będzie na wklęsłym:
Ft wkl = µ N +
𝑚𝜈 2
𝑅
> Ft wyp = µ N −
𝑚𝜈 2
𝑅
Zadanie 3
(wg Jędrzejewski, Kruczek, Kujawski)
Na (poziomej) tarczy o momencie bezwładności Io przymocowano w
jednakowych odległościach R od ułożyskowanej osi dwa jednakowe
wentylatorki o masach m (osie śmigieł wentylatorów są równoległe do osi
tarczy) Załóżmy, że wentylatorki są np. dla astmatyków, zasilane bateryjnie.
Po uruchomieniu wentylatorków tarcza zaczęła się obracać (model
niewłaściwie skonstruowanego 2-silnikowego samolotu śmigłowego!)
Każde śmigło (z wirnikiem) ma moment bezwładności Is względem własnej
osi i wiruje z prędkością kątową ωs wzgl. tarczy.
Obliczyć prędkość kątową ωt tarczy?
Rozwiązanie
Z zasady zachowania momentu pędu:
2Is
ωt = - ωs I + 2mR2 +2I
o
s
(Io + 2mR2 + 2Is) ωt = - 2 Isωs
Zadanie 4
(wg Falandysz)
Jednakowe kropelki cieczy (wody), każda o promieniu 0,1 mm połączyły
się, tworząc dużą kroplę o promieniu 2 mm. Jak wielka energia wydzieliła
się podczas tego połączenia? Współczynnik σ napięcia powierzchniowego
dla wody wynosił w tym przyp. 7,2*10-2 N/m
Jeśli zwiększymy pole powierzchni swobodnej cieczy o ΔS (przy stałej temperaturze),
działając przeciwko sile napięcia powierzchniowego F = σl to
wykonujemy pracę W
= ς*ΔS
Rozwiązanie
Istnieje tu analogia do nukleonów izotopów wodoru łączących się w hel podczas jądrowej reakcji
termonuklearnej!
Pole powierzchni kuli = poczwórnemu polu koła wielkiego więc
na utworzenie dużej kropli potrzebna jest praca Wd
a na utworzenie n kropelek – praca: Wm
= ς*4πR2
= n*ς*4πr2
(Mamy tu, dla bryły, tylko jedną błonkę a nie ich parę, jak dla powierzchni i figur)
4
Liczbę kropelek można obliczyd z przyrównania objętości: n*
3
4
πr3 = πR3
3
R3
Stąd n= 3
r
𝑅
3
Albo: n
=
Albo: n
R
= r R2
𝑟
=
2
0,1
3
= 203 = (2*10)3 = 23*103 = 8000
Mamy: Wm
R
= r R2 *ς*4πr2 > Wd = ς*4πR2
R
Wm = r Wd = 20Wd
ΔW = Wm - Wd = 4πςR2
𝑅
𝑟
−1
ΔW ≈ 4*3*7*10-2 *(2*10-3)2 *(20-1)
ΔW ≈ 4*21*10-2 *4*10-6*20
ΔW ≈ 100*80*10-8
ΔW = … ≈ 8*10-5 J (a dokładnie: 6,87*10-5)
Zadanie 5
()
Po piasku człowiek przemieszcza się (biegnie) szybciej niż płynie w wodzie;
Załóżmy, ze dwa razy. Ratownik, znajdujący się na plaży w odległości 30
metrów od prostoliniowego brzegu morza, zobaczył przez lornetkę z
dalmierzem potrzebującego pomocy człowieka w odległości 85 metrów od
siebie; Kierunek między obydwoma ludźmi był skośny do brzegu – taki, że
zmierzona na tym kierunku odległość od ratownika do brzegu wynosiła 50
metrów.
Ile metrów po linii prostej powinien biec ratownik aby jak najszybciej
znaleźć się przy tonącym?
Rozwiązanie
…zadania jest uciążliwe matematycznie więc sprawdźmy tylko prawidłowośd rozwiązania: 65 metrów
Dla każdej pary prędkości, nie tylko dla prędkości światła (w prawie załamania) oraz dla każdej pary
środowisk (nie tylko przezroczystych) obowiązuje (tzw. Zasada najmniejszego działania, zasada
Fermata):
v1 sinα
v2 = sinβ
Gdzie α jest kątem padania (ze środowiska 1 do 2)
natomiast β jest kątem załamania.
Kąty są odmierzane do wspólnej prostopadłej do granicy ośrodków wystawionej w punkcie
przekraczania ośrodków
U nas
sinα
sinβ = 2
Do obu funkcji trygonometrycznych musimy obliczyd odpowiednie boki:
Wymiary: 30 i 50 tworzą trójkąt prostokątny (jedną z przyprostokątnych i przeciwprostokątną
odpowiednio). Obliczmy drugą przyprostokątną (podstawiajmy wymiary zredukowane 10 razy) –
wzdłuż brzegu:
Z tw. Pitagorasa:
52 − 32 = 25 − 9 = 16 = 4 (złoty trójkąt)
Wymiary: 30 i 65 tworzą drugi trójkąt prostokątny (jedną z przyprostokątnych i przeciwprostokątną
odpowiednio). Obliczmy drugą przyprostokątną (odległośd od rzutu na brzeg ratownika do punktu
wejścia ratownika do wody) – wzdłuż brzegu:
6,52 − 32 ≈ 45 − 9 = 36 = 6
Z tw. Pitagorasa:
Mając obliczony wymiar 4 oraz odległości: 5 i 8,5 z tw. Talesa możemy obliczyd odległośd od rzutu
ratownika na brzeg do rzutu na ten brzeg tonącego:
5 4
8,5 = p
stąd
p=
8,5*4
5 ≈7
Mając wymiary : 6 i 7 można obliczyd odległośd od rzutu na brzeg tonącego do punktu wejścia
ratownika do wody:
7–6=1
sinα
sinβ =
6
6,5
1
12+m2
czyli trzeba wyznaczyd jeszcze (prostopadłą) odległośd m tonącego od brzegu
5
3
8,5 = 3+m
– ponownie z tw. Talesa:
Stąd
5m = 25,5 – 15
czyli m = 10,5/5 ≈ 2
sinα 6 2,2
sinβ = 6,5 1 ≈ 2 co było do sprawdzenia!
Obliczmy czas dostania się ratownika do tonącego po tym
najkorzystniejszym, łamanym w powyższy sposób, torze:
s
V=t
stąd
s
t=v
T = t 1 + t2 =
6,5 2
2 +1=
5,25 jednostek czasu
Dla porównania obliczmy czas po drodze niełamanej:
5
T = t 1 + t2 = 2
8,5-5
+ 1 = 2,5+3,5 =
6 > 5,25 jednostek czasu!
Szybciej (od niełamanej drogi) byłoby nawet wtedy gdyby ratownik
biegł do prostokątnego rzutu na brzeg tonącego:
T = t 1 + t2 =
32+72 2
9+49
58
7,5
+
=
+2
=
+
2
≈
2
1
2
2
2 +2=
5,75 < 6 jednostek czasu!
Zadanie 6
(wg Falandysz)
Antena odbiorcza fali elektromagnetycznej ma długość 1,33 m. Jak trzeba
zmienić długość anteny aby odbierała te same fale zanurzona w wodzie?
Współczynnik załamania przez wodę fal o takiej długości wynosi 9
Rozwiązanie
Długośd anteny odbiorczej powinna byd taka jak połowa długości odbieranej fali.
Natomiast podany współczynnik załamania jest bezwzględnym - jest on stosunkiem prędkości fali w
powietrzu do prędkości fali w ośrodku gęstszym – wodzie
Od ośrodka nie zależy częstotliwośd fali
Mamy więc:
V = λf
v
stąd f = λ
fp = fw
vp vw
λp = λw
vp vw
2lp = 2lw
lp vp
lw = vw
vp
vw = n
lp
Stąd: l = n
w
Czyli:
lp
lw = n
=
1,33
9
= 0,148 m = 14,8 cm
Zadanie 7
(wg Jędrzejewski, Kruczek, Kujawski)
Dwie naładowane kulki o gęstości ρK każda wiszą na nitkach tworzących ze
sobą kąt 2α. Po zanurzeniu w cieczy dielektrycznej o gęstości ρC kąt
rozchylenia nitek zmienił się do wartości 2β. Obliczyć względną
przenikalność elektryczną εR cieczy
Rozwiązanie
Mamy obliczyd ε0.
Na kulki działają po 3 siły: w poziomie: odpychania Coulomba a w pionie: ciężaru oraz wyporu, przy
czym wypór w powietrzu pominiemy jako mały. Wypadkowa siły poziomej FQ i wypadkowej w pionie
F ma kierunek odpowiednio każdej z obu nici.
q2
FQ = 4πε ε R2
0 R
W powietrzu εR = 1
Gdy przez L oznaczymy długośd każdej nitki to:
R/2
Sinα = L
Stąd: R = 2Lsinα
q2
Czyli: FQ = 4πε ε (4L2sin2α)
0 R
Ciężar to iloczyn masy i objętości
a masa to gęstośd mnożona przez objętośd.
W powietrzu:
F = mg = ρKV *g
Siła wyporu to masa wypartego płynu pomnożona przez przyspieszenie ziemskie
Gdzie masa to gęstośd cieczy razy objętośd kulki
W oleju:
F = mg – ρCV*g = (ρK - ρC)Vg
FQ
F = tgα
oraz w oleju:
FQ
F = tgβ
q2
tgα = 16π L2ε *1*sin2α / (ρK*Vg)
0
q2
tgβ = 16π L2ε *ε sin2β / ((ρK – ρC)*Vg)
0
R
tgα
tgβ =
1
sin2α
1
ρK
sin2α ρK - ρC ρK - ρC sin2β
1 = ρK
1 = ρK εRsin2α
2
εRsin β
εRsin2β
ρK - ρC
tgα ρK sin2α
Stąd εR = tgβ ρ - ρ sin2β
K
C
Czyli:
ρK tgα sin2α
εR = ρ - ρ tgβ sin2β
K
C
Zadanie 8
(wg Jędrzejewski, Kruczek, Kujawski)
Do jakiego potencjału należy naładować dwie kule o masach m = 1000 kg i
promieniach R = 1 m aby siła odpychania kulombowskiego tych kul była
równa sile ich przyciągania grawitacyjnego?
Pojemnośd elektryczna kuli wynosi: C
= 4πε0εRR
gdzie εR = 1 (w powietrzu jak w przybliżeniu w próżni)
Rozwiązanie
Ładunek kuli:
Q = CV
gdzie v jest szukanym potencjałem
Q2
Gm2
4πε0εRR2 = R2
(4πε0εRR*V)2 Gm2
4πε0εRR2 = R2
4πε0εRR2V2 = Gm2
V2
m2
Stąd G = 4πε ε R2
0 R
(Możnaby obliczyd wartośd stałej grawitacji gdyby mied równoważącą wartośd potencjału)
m
V = 2R
G
πε0εR
R=R/2 + R/2 = 1
ε0 = 8,85*10-12
G = 6,67*10-11
m = 10
103
2*1
3
6*10-11
103
3*9*10-12*1 = 2
V ≈(750 do 800) V (V=775
2*10 103
9 ≈ 2*3 20
Voltów)
Zadanie 9
(wg Jędrzejewski, Kruczek, Kujawski)
Jak należy rozdzielić ładunek Q na dwie kulki aby siła odpychania się tych
kulek była największa?
Rozwiązanie
Q1(Q-Q1)
F = 4πε ε R2
0 R
Iloczyn Q1(Q-Q1) jest wielomianem II stopnia względem Q1. Taka
funkcja osiąga maksymalną wartośd dla zmiennej Q1równej średniej
arytmetycznej miejsc zerowych funkcji. Jednym z miejsc zerowych jest Q1=0 a
drugie wynika z równania: Q-Q1=0 czyli Q1 = Q
0+Q Q
2 =2
Więc F = Fmax gdy Q1 = Q/2 = Q2
Zadanie 10
(wg Jędrzejewski, Kruczek, Kujawski)
Przewód elektryczny o długości L biegnący w izolowanej od niego
metalowej rurce został zwarty z tą osłoną w nieznanym miejscu. Położenie
punktu zwarcia wyznaczono przeprowadzając pomiary natężenia prądu na
obu końcach tych przewodników za pomocą tego samego źródła prądu o
pomijalnie małym oporze wewnętrznym. Okazał się, że natężenie na
jednym z końców (A) było większe N razy od prądu na końcu drugim. W
którym miejscu nastąpiło zwarcie ?
Rozwiązanie
Oznaczmy przez x np. od punktu A szukaną odległośd a przez R – sumaryczną rezystancję
(połączonych szeregowo na jednym z kooców przed zwarciem) przewodu i osłony.
Wtedy rezystancja obwodu zwarciowego po stronie punktu A będzie wynosid R1=
xR a rezystancja
analogicznego obwodu po drugiej stronie będzie R2=(L-x)R. Odpowiednie prądy z prawa Ohma
wynosid będą: I1=U/R1 oraz I2=U/R2.
Mamy I1=NI2
Czyli:
U
U
=
N
xR
(L-x)R
Stąd
Nx = L - x
Nx+x=L
x(N+1)=L
L
x = N+1
Zadanie
(wg Jędrzejewski, Kruczek, Kujawski)
Równolegle połączono dwie baterie 3-ogniwowe ale okazało się, że jedno z
ogniw w jednej z baterii jest zwarte. Każde z pozostałych ogniw ma siłę
elektromotoryczną ε=2V oraz opór wewnętrzny r=0,1 Ω. Znaleźć napięcie
między biegunami takiego zestawu baterii
Rozwiązanie
W gałęzi o mniejszej liczbie ogniw czyli w gałęzi 2ogniwowej prąd I
wewnątrz baterii płynie od bieguna dodatniego do ujemnego. Stąd
spadek napięcia (2r*I) na rezystancji wewnętrznej tej gałęzi dodaje
się (a nie odejmuje) do S.EM. 2ε
(Na podstawie napięciowego – IIgo - prawa Kirchhoffa mamy)
3ε – 3r*I = 2ε + 2r*I
Lewa lub prawa strona równania jest szukanym napięciem
Trzeba wpierw wyznaczyd prąd I - z („całego”) powyższego równania:
3rI + 2rI = 3ε - 2ε
5rI = ε
ε
I = 5r
Napięcie wyznaczmy np. z lewej strony równania (z prawa Kirchhoffa):
ε
U = 3ε – 3r5r
3
U = ε(3 - 5 )
U = 2,4ε
U = 2,4 * 2
U = 4,8 V
2*2V < 4,8V < 3*2V
Zadanie
(wg Jędrzejewski, Kruczek, Kujawski)
Kulka naładowana ładunkiem q1>0 leży na nieprzewodzącej płycie. Na jaką
odległość h należy zbliżyć z góry drugą kulkę naładowaną ładunkiem q2<0
aby pierwsza kula oderwała się od płyty. Masa kulki leżącej wynosi m.
Opisać ruch przyciąganej kulki jeśli obie są przewodzące?
Rozwiązanie
Kulka poruszad się będzie ze wzrastającym przyspieszeniem i po zetknięciu z górną kulką opadnie na
płytę (bo przekaże swój ładunek górna dolnej zobojętniając ją /i siebie/)
q1|q2|
4πε0εRh2 ≥ mg
Stąd
h≤
q1|q2|
4πε0εRmg
Zadanie
(wg Jędrzejewski, Kruczek, Kujawski)
Czy izolowana kula o masie M=1000 kg naładowana taką ilością
elektronów, że ich sumaryczna masa wynosi m=1 g mogłaby zostać
oderwana od Ziemi siłą przyciągania takiego samego ładunku dodatniego
umieszczonego w odległości takiej jak do Słońca czyli 150 mln km?
Rozwiązanie
Siła kulombowska musiałaby pokonad siłę ciężkości M*g:
Mg = 103 * 9,81 (w przybliżeniu bo np. nie uwzględniamy masy elektronów nadmiarowych)
Liczba elektronów jest równa:
m
me gdzie me jest masą elektronu
Ich ładunek będzie równy:
m
me e gdzie e jest ładunkiem elektronu
Siła elektrostatyczna wynosi: F =
m
(m e)2
e
4πε0εRR2 =
e= 1,60 *10-19
me = 9,11*10-31
εR = 1
ε0 = 8,85*10-12
e
11
me = 1,8*10
(1,8*1011*10-3)2
F=
4*3,14*8,85*10-12*1*(1,5*1011)2
1,82*1016
F = 4*3,14*8,85*10-121,52*1022
e
(m m)2
e
4πε0εRR2
1,82*1016
1,82*106
F ≈ 4*3*9*1,52*1010 ≈ 100*1,52 ≈
1,8
1,5 > 0,98
(F = 1,2 *104)
0,98*104 N < 1,2 *104 N
Więc oderwie się!
1,82 4
1,52 10
Zadanie
(wg Jędrzejewski, Kruczek, Kujawski)
Obliczyć siłę F wzajemnego przyciągania się okładek kondensatora
płaskiego powietrznego oddalonych o d=1 µm jeśli kondensator
naładowano do napięcia V = 1 V a każda z okładek ma powierzchnię s =
0,01 m2
Rozwiązanie
F = EQ gdzie E jest natężeniem pola elektrycznego
Natężenie pola E0 wytwarzane przez cały kondensator =
V
d
E0
2
Więc wytwarzane przez każdą z okładek wynosi E=
Ładunek na okładzinie wynosi:
Q=CV
Pojemnośd kondensatora płaskiego wynosi
S
C=ε0εrd
Z powyższych 5 wzorów mamy:
s
Q= ε0εrd V
V
E=2d
A z powyższych dwóch:
V
s
F=2d ε0εrd V
czyli:
εR
s
F = 2 ε0V2d2
-2
1
-12
2 10
F =2 *8,85*10 *1 *(10-6)2
F = 4,425*10-2 N
8,85
F = 2 *10-2
Zadanie
(wg Chrapkowska, Kaczorowska)
Bombka choinkowa o średnicy d=12 cm wytwarza obraz okna. Wysokość
okna wynosi h=1,5 m a wysokość obrazu okna: h’=0,8 cm. W jakiej
odległości od okna stoi choinka?
Rozwiązanie
Mamy do czynienia ze zwierciadłem wypukłym
Równanie ogólne zwierciadła (soczewki):
1 1 1
x+y=f
R
f=2
d
R=2
Z powyższych wzorów:
Dodatkowo powiększenie:
Skąd
1 1 4
x+y=d
h x
h' = y
h'
y= x h
Po dostosowaniu znaków mamy:
Czyli:
h'-h 4
xh' = - d
d
Xh’= - 4 (h’-h)
1 1
4
=
x |y| d
1 h
4
=
x xh' d
d h-h'
X=4 h'
albo
d h
X=4 (h' -1)
0,12 1,5
X= 4 (0,008 -1)
1,6
X≈0,03(0,008 -1)
X≈0,03(200-1)
x≈0,03*200
x≈6 m
(dokładniej 5,995 m)
Zadanie
(wg M. K.)
Do jednego gniazdka włączono jednocześnie 3 żelazka o mocy 1500 W
każde. Na odległości L=10 m od gniazdka do oprawy bezpiecznikowej
średnica przewodu miedzianego wynosi 1 mm. Gęstość Cu wynosi ρ=8,93
g/cm3 a jej ciepło właściwe c=0,092 cal/(g*stop) Bezpiecznik jest zwarty
tym samym przewodem z powodu beztroskiej „naprawy”. Temperatura
otoczenia wynosi 200C.
Znaleźć zależność między temperaturą t przewodów a czasem τ i oszacować
po jakim czasie temperatura przewodów wyniosłaby 100 oC?
Rozwiązanie
4,19
C=0,092 10-3 = 0,38548*103
10-3
Ρ=8,93(10-2)3 =8,93*103
E'
P= τ
E’=3E
E=Q=mc(t-20)
m=ρV
V=2*(L*s)
S=πR2
d
R=2
Z powyższych wzorów mamy:
πd2
3Pτ=ρ*2L 4 c(t-20)
4*3Pτ
t-20=ρ2Lπd2c
6Pτ
t= πρcLd2 +20
6*1500τ
t= 3,14*8,93*103*0,38548*103*10*(10-3)2 +20
6*15*102τ
t≈ 3*9*103*0,36*103*10*10-6 +20
6*15*102τ
t= 3*9*0,36*10 +20
2*5*10τ
t= 1*3*0,36 +20
2*5*10τ
t= 1*3*0,36 +20
t≈100τ+20
Już po ok. jednej sekundzie!
…
Zadanie
(wg M. K.)
Np. stary radioodbiornik kieszonkowy odbierający tylko fale średnie (w
tym Program II Polskiego Radia państwowego) może być dostosowany
amatorsko również do odbioru programu radiofonicznego Warszawa I na
falach długich poprzez dołączenie (poprzez miniaturowy przełącznik)
kondensatora Cx równolegle do kondensatora strojeniowego C (modulacji
amplitudy AM) Jaki jest stosunek Cx/C (/Konkretną/ wartość C można
odczytać z nadruku na tym kondensatorze) jeśli częstotliwość f1 Programu I
wynosi 0,225 MHz a częstotliwość f2 programu Warszawa II wynosi 1,388
MHz?
Rozwiązanie
Wygodnie byłoby aby przy przełączaniu programów nie obracad (a praktycznie: obracad niewiele)
pokrętłem powietrznego kondensatora strojeniowego, dlatego zmienimy częstotliwośd rezonansową
z częstotliwości f1 a nie np. z (niepodanego zresztą w danych zadania) kooca lub środka zakresu fal
średnich. (Normalnie dla zakresów AM podaje się długości fal – np. dla Warszawy I jest to 1339 m; Tu
już zostały te długości np. dla wygody oraz porównania z częstotliwościami programów FM
zamienione na częstotliwości - z wzoru: c = λf)
f2 =
1
2π LC
Przy równoległym połączeniu kondensatorów ich wartości się dodają więc:
f1 =
1
2π L(C+Cx)
Ze wzoru na f2 wyliczymy nieznaną indukcyjnośd L
1
LC = 2πf
2
1
L = (2πf )2C
2
Przekształdmy nieco wzór na f1 I wstawmy doo L:
1
L(C+ Cx )= (2πf )2
1
1
1
(2πf2)2C (C+ Cx) = (2πf1)2
C+Cx f22
C = f12
Cx f2
1+ C = (f )2
1
Cx f 2 2
C = (f1 ) – 1
Cx 1,388 2
C = (0,225 ) – 1
Cx
2
C = (6,16(8)) – 1
Cx
2
C ≈ (6) – 1
Cx
C ≈ 35
(Są to pojemności rzędu pF)
Zadanie
(wg M. K.)
Załóżmy, że wysokość muzyka (a dokładniej – odległość do poziomu jego
ust) wynosi 1,69 m. Muzyk ma grać na instrumencie dętym, który ma m. in.
wydobywać najniższy dźwięk. Piszczałka (otwarta) instrumentu ma być
zwinięta na kształt sprężyny walcowej aby instrument miał zwartą budowę
(muzyk mógł wygodnie zawieszać go na ramieniu). Ile min. zwojów będzie
miał instrument?
Rozwiązanie
Najniższy dźwięk ma częstotliwośd f=16
Hz. Trzeba obliczyd dpowiadającą mu długośd fali
λ = v/f
W piszczałce otwartej fala stojąca może mied min. 2 dwiartki czyli połówkę długości fali akustycznej
Mamy więc
λ v
2 = 2f
Jednocześnie
gdzie v = prędkośd dźwięku
λ
2 = (2r*π)*x
v
Stąd: 2f = (2r*π)*x
v
X = 2*f*2r*π
340
X = 2*16*1,7*3,14
X≈2
Zadanie
(wg Leyki i Szmeltera.)
Lina służąca do przywiązywania statków na przystani nawijana jest na
słupek w tym celu aby marynarz ciągnąc za jeden koniec liny siłą S2 mógł
utrzymać statek, do którego przymocowany jest drugi koniec liny. Ile razy
musi marynarz okręcić linę na słupku, by mógł siłą S2 = 20 N utrzymać
statek, ciągnący za drugi koniec liny siłą S1 = 1 kN. Współczynnik tarcia liny o
słupek: µ = 0,2
Tarcie cięgien (lin, taśm w hamulcach) o krążki (tarcze) opisuje tzw. wzór
Eulera S1 ≥ S2eµα
(lub S2 ≥ S1e-µα)
Gdzie e
≈ 2,72 jest podstawą logarytmów zwanych naturalnymi (ln)
natomiast α jest tzw. kątem opasania, który musi byd podstawiony w
radianach
µ jest współczynnikiem (rozwiniętego) tarcia statycznego
Jak widad brak tu zależności od wymiarów krążka (średnicy i szerokości/grubości); jest tylko
(pośrednia) zależnośd od długości opasania
Rozwiązanie
S1 / S2 ≥ eµα
Obie strony trzeba zlogarytmowad: loge (S1 / S2) = ln(S1 / S2) = µα
Czyli α =
ln(S1 / S2) ln(100
=
µ
kG / 2 kG) ln50 4
= 0,2 ≈ 0,2 = 20 rad
0,2
20 10
Liczba opasao: 2π = π ≈ 3,3
(przy dokładniejszych obliczeniach, począwszy od ln50 : 3,11)
Ln50 można np. obliczyd (50 ln) w Kalkulatorze Windows (Naukowym)
Praktyczna liczba opasao: 4
Zadanie
(wg M. K.)
Cowboy owinął skórzane pasy wodzów konia o poziomą żerdź zbudowaną
przy wejściu do saloon’u. Ile owinięć musiał zrobić jeśli minimalnie
zwisający koniec wodzów waży 6 Gramów a koń ciągnie z siłą 60 kG
Współczynnik tarcia liny o żerdź przyjąć: µ = 0,8
Tarcie cięgien (lin, taśm w hamulcach) o krążki (tarcze) opisuje tzw. wzór
Eulera S1 ≥ S2eµα
(lub S2 ≥ S1e-µα)
Gdzie e
≈ 2,72 jest podstawą logarytmów zwanych naturalnymi (ln)
natomiast α jest tzw. kątem opasania, który musi byd podstawiony w
radianach
µ jest współczynnikiem (rozwiniętego) tarcia statycznego
Jak widad brak tu zależności od wymiarów krążka (średnicy i szerokości/grubości); jest tylko
(pośrednia) zależnośd od długości opasania
Rozwiązanie
Rozwiązanie
S1 / S2 ≥ eµα
Obie strony trzeba zlogarytmowad: loge (S1 / S2) = ln(S1 / S2) = µα
Czyli α =
ln(S1 / S2) ln(60
=
µ
kG / 0,006 kG) ln10000 9,2
= 0,8 ≈ 0,8 ≈ 12 rad
0,8
12 6
Liczba opasao: 2π = π ≈ 2
Ln10000 można np. obliczyd (10000 ln) w Kalkulatorze Windows (Naukowym)
Praktyczna liczba opasao: 2
Zadanie
(wg M. K.)
W numerze cyrkowym gimnastyk po wspięciu się na zwisającą linę owija
nią część swego ciała aby wytworzyć siłę tarcia niezbędną do wykonywania
ewolucji. Na dole stoi pomocnik naprężający dolny koniec liny. Gimnastyk
waży 81 kG a pomocnik napręża linę siłą 3 kG. Ciężaru własnego liny nie
uwzględniać. Współczynnik tarcia liny o ciało człowieka przyjąć: µ = 0,5.
Obliczyć ile zwojów liny musi mieć na sobie gimnastyk aby się nie zsunął z
liny
Tarcie cięgien (lin, taśm w hamulcach) o krążki (tarcze) opisuje tzw. wzór
Eulera S1 ≥ S2eµα
(lub S2 ≥ S1e-µα)
Gdzie e
≈ 2,72 jest podstawą logarytmów zwanych naturalnymi (ln)
natomiast α jest tzw. kątem opasania, który musi byd podstawiony w
radianach
µ jest współczynnikiem (rozwiniętego) tarcia statycznego
Jak widad brak tu zależności od wymiarów krążka (średnicy i szerokości/grubości); jest tylko
(pośrednia) zależnośd od długości opasania
Rozwiązanie
Rozwiązanie
S1 / S2 ≥ eµα
Obie strony trzeba zlogarytmowad: loge (S1 / S2) = ln(S1 / S2) = µα
Czyli α =
ln(S1 / S2) ln(81
=
µ
kG / 3 kG) ln27 3
= 0,5 ≈ 0,5 ≈ 6 rad
0,5
6 rad 3
Liczba opasao: 2π rad = π ≈ 1
Bezpieczna liczba opasao: 2 albo można zaufad pomocnikowi, że zwiększy naciąg (szybko)
Zadanie
(wg M. K.)
Jak długi musi być najbardziej donośny gwizdek w postaci piszczałki
otwartej?
Rozwiązanie
Najlepiej słyszalna jest częstotliwośd
3 kHz (1 kHz na części liniowej wykresu)
Weźmy 2 kHz
Odpowiadająca połówka długośd fali wynosi:
λ v
340
=
=
2 2f 2*2000 = 0,085 m
Zadanie
(wg M. K.)
Jaka powinna być orbita geostacjonarna Wenus jeśli masa Wenus wynosi
4,869 *1024 kg a okres jej wirowania wokół swojej osi T = 243 dni ziemskie?
Orbita geostacjonarna Ziemi wynosi 42,5 tys. km.
Masa Ziemi = 5,98 = 1024 kg
Odległośd Ziemi od Wenus wynosi ok. 42 mln. km
Rozwiązanie
Wzór na promieo orbity geostacjonarnej dostaje się z przyrównania siły grawitacji z odśrodkową oraz
zastępując prędkośd liniową wzorem zawierającym okres T. (Dla Ziemi) wynosi on
…
M (2π)2R2
G R = T2
3
G
2
2*TZ *MZ
(2π)
RZ=
(Nie mamy /podanej w treści/ stałej grawitacji ale) Widad, że
RW ≈ RZ*
3
2432*5/6
≈ RZ*
3
50000
≈ RZ*10
3
50
≈ 36 RZ
Czyli znacznie więcej dla Wenus niż dla Ziemi
≈ 36 * 42,4 tys km ≈ 1,5 mln km
Jest to też znacznie więcej oczywiście niż wynosi grubośd atmosfery Wenus
Jest to już ok. 5 sekund świetlnych … (opóźnienie i słaba moc sygnału)
5 razy więcej niż wynosi orbita Księżyca
Zadanie
(wg M. K.)
Współczynnik oporu aerodynamicznego (współczynnik kształtu) dla
płaskiej płytki wynosi cD=1,1 a dla profilu lotniczego cU= 0,04. Ile razy w
przybliżeniu siła oporu D jest większy od siły nośnej U samolotu?
D oraz U wyrażają się praktycznie tym samym wzorem:
D= 0,5CDρSv2
U= 0,5CUρSv2
Gdzie:
S jest polem powierzchni poprzecznej do kierunku ruchu
z prędkością v
ρ jest gęstością płynu (powietrza)
Rozwiązanie
CD/CU = 27
Zadanie
(wg M. K.)
Porównajmy siły przyciągania grawitacyjnego Księżyca przez Słońce FS i
przez Ziemię FZ
GMSm
FS = R 2
s-z
Bo Rs-k ≈ Rs-z gdyż Rs-z >> Rz-k (150 mln km >>385 tys km)
GMZm
FZ= R 2
Z-K
Gdzie m jest masą Księżyca
Po podzieleniu stronami oraz uwzględniając Ms/Mz = 333400:
FS MS RZ-K 2
FZ = MZ (RS-Z )
0,5 mln km
0,1
0,01
0,01
≈ 300 000 * (150 mln km )2 = 300000 * ( 30 )2 = 300000 * 900 ≈ 300000 * 1000
FS
FZ = 3 > 1
Więc Księżyc jest przyciągany silniej przez Słooce niż przez Ziemię!
(Gdyby obliczyd dokładniej a nie szacunkowo to stosunek byłby bliższy liczbie 2 )
Więc dlaczego Słooce nie przejmie Księżyca od Ziemi?!
Obliczmy prędkośd liniową Księżyca na orbicie wokółziemskiej.
Przyrównujemy w tym celu siłę dośrodkową z siłą grawitacji:
vk2m GMZm
Rz-k = Rz-k2
Stąd: vk =
Vk ≈
6*6*107
400 =
GMz
Rz-k =
6,67*10-11 * 6*1024
384*106
6*6*106*10
≈
400
6*6*106*9 18 3 20 3
= 20 10 ≈ 20 10 m/s
400
Vk ≈ 1 km/s
Analogicznie można obliczyd prędkośd liniową Ziemi wokół Słooca:
Stąd: vz =
Vz ≈
12*109
15 =
GMS
Rs-z =
6,67*10-11 * 2*1030
150*109
12*10*108
≈ 9*108 = 3*104
15
Vz = 30 km/s
(< VIII = 40 km/s)
Gdyby Słooce miało przejąd Księżyc od Ziemi to Księżyc miałby
promieo orbity wokółsłonecznej taki jak Ziemia. Obliczmy jaką
prędkośd liniową miałby Księżyc w ruchu wokół Słooca po orbicie
Ziemi; Masa Księżyca jest 81 razy mniejsza od masy Ziemi tak więc
siła dośrodkowa byłaby tyleż mniejsza. Siła dośrodkowa jest też
proporcjonalna do kwadratu prędkości więc prędkośd byłaby 81 razy
mniejsza od prędkości 30. Prędkośd Księżyca wynosiłaby więc 30/9
czyli ok. 10 razy mniej od 30 czyli 3 km/s.
Porównując siły dośrodkowe ‘do’ Ziemi i ‘do’ Słooca na ‘wysokości’
Księżyca bierzemy stosunek kwadratów szybkości: 32/12 = 9. Tyle
samo musiałby wynieśd stosunek sił przyciągania. Widad, że
stosunek: 2 < 9 nie wystarczy, aby ukraśd Księżyc ;-) Musiałby wynosid
więcej o rząd wielkości!
Księżyc zawdzięcza krążenie wokół Ziemi okolicznościom swego
powstania.
Zresztą Księżyc pośrednio krąży wokół Słooca – z Ziemią! ;-)
Dzięki Wilder za treściwe podtrzymywanie wątku! :-)))
Prędkośd na orbicie nie powinna zależed od masy satelity rzeczywiście a
mnie jakby wyszła taka zależnośd... Hmmm... nie wiem gdzie błąd zrobiłem w rozumowaniu...
Prędkośd Księżyca
musiałaby wzrosnąd do II kosmicznej czyli stosunek sił odśrodkowych
a więc i badany stosunek przyciągao grawitacyjnych byłby: (8
km/s)^2/(1 km/s)^2 = 64 >> 2
No ale jam uparty ;-) Bo w takim razie co powiesz na takią zmianę:
Czyli przyciąganie solarne musiałoby byd prawie dwa rzędy wielkości
większe a nie dwukrotnie!?
W kwestii nazewnictwa - niechlujnośd moja ;-)
Ciekawie wątek rozwijasz na dwa ciekawe anonse: max. promieo stabilnej orbity satelity Ziemi (i jego
ewentualna zależnośd od kierunku krętu satelity) oraz Merkury byłym (satelitą ;-) Wenus!