Informacja do zadań 1

Informacja do zadań 1. i 2.
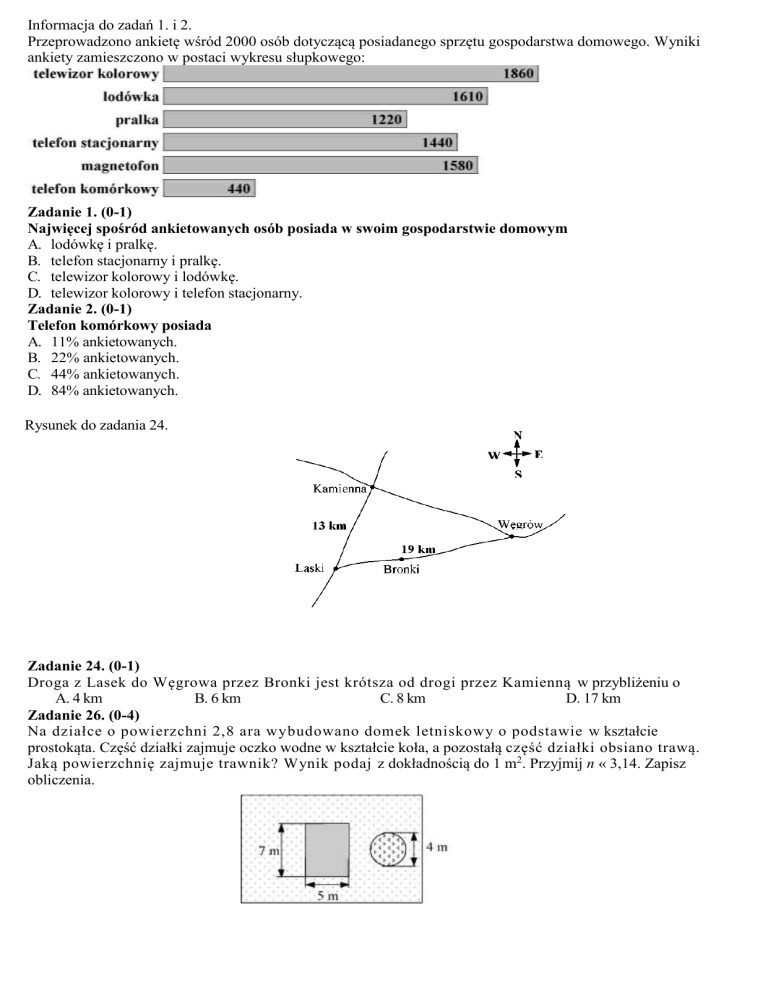
Przeprowadzono ankietę wśród 2000 osób dotyczącą posiadanego sprzętu gospodarstwa domowego. Wyniki
ankiety zamieszczono w postaci wykresu słupkowego:
Zadanie 1. (0-1)
Najwięcej spośród ankietowanych osób posiada w swoim gospodarstwie domowym
A. lodówkę i pralkę.
B. telefon stacjonarny i pralkę.
C. telewizor kolorowy i lodówkę.
D. telewizor kolorowy i telefon stacjonarny.
Zadanie 2. (0-1)
Telefon komórkowy posiada
A. 11% ankietowanych.
B. 22% ankietowanych.
C. 44% ankietowanych.
D. 84% ankietowanych.
Rysunek do zadania 24.
Zadanie 24. (0-1)
Droga z Lasek do Węgrowa przez Bronki jest krótsza od drogi przez Kamienną w przybliżeniu o
A. 4 km
B. 6 km
C. 8 km
D. 17 km
Zadanie 26. (0-4)
Na działce o powierzchni 2,8 ara wybudowano domek letniskowy o podstawie w kształcie
prostokąta. Część działki zajmuje oczko wodne w kształcie koła, a pozostałą część działki obsiano trawą.
Jaką powierzchnię zajmuje trawnik? Wynik podaj z dokładnością do 1 m2. Przyjmij n « 3,14. Zapisz
obliczenia.
Dane z ogłoszenia wykorzystaj do rozwiązania zadań 30., 31. i 32.
Zadanie 30. (0-2)
Ułóż wzór funkcji przedstawiającej zależność całkowitego kosztu wynajęcia autokaru od
liczby przejechanych kilometrów. Opisz użyte zmienne.
Tabela odległości do zadania 31.
Katowice
74 km
Wadowice
88 km
14 km
92 km
18 km
Kalwaria Zebrzydowska
Kalwaria Zebrzydowska
przez Stryszów
Zadanie 31. (0-3)
Oblicz koszt wynajmu autokaru na trasę:
Zadanie 32. (0-3)
Każdy z 25 uczestników jednodniowej wycieczki wpłacił kwotę 20 zł na pokrycie opłat za autokar i
przewodnika. Ile kilometrów liczyła trasa wycieczki? Zapisz obliczenia.
Zadanie 36. (0-3)
Uczniowie piszący egzamin rozmieszczeni są w salach w następujący sposób: 48 uczniów w sali
gimnastycznej, pozostali w salach lekcyjnych po 15 osób. Gdyby w każdej sali lekcyjnej egzamin pisało
o dwóch uczniów mniej, to zdający zajęliby o jedną salę lekcyjną więcej, a na sali gimnastycznej
musiałby pisać jeden uczeń więcej. Ilu uczniów klas trzecich było w gimnazjum? Zapisz obliczenia.
Zadanie 10 (0 - 1)
Regaty odbywają się na trasie liczącej y kilometrów. Jacht płynący w czasie x godzin z szybkością 30
km/h ma jeszcze do pokonania drogę długości dwóch kilometrów. Który
z poniższych wzorów opisuje długość trasy regat?
1
x2
A. y = 30x+2
B. y = 30x
C. y = 30x-2
D. y 
30
Zadanie 8. (0-1)
Po jeziorze pływa jacht z rozwiniętymi żaglami. Jaka jest powierzchnia tych żagli?
A.
3,9 m2
B.
5,2 m2
C.
5,85 m2
D.
10,4 m2
Zadanie 9. (0-1)
Wykres przedstawia temperaturę powietrza w dniu regat w godzinach 1000 - 1300. Regaty rozpoczęły się
o godzinie 1100 i trwały 100 minut. Jakie była różnica temperatury powietrza między godzinami
zakończenia i rozpoczęcia regat ?
Zadanie 11. (0-1)
Lina długości 13 metrów podtrzymuje pionowo ustawiony maszt i jest umocowana do pokładu
w odległości 5 metrów od podstawy masztu. Na jakiej wysokości od pokładu jest umocowana na
maszcie lina?
Zadanie 12. (0-1)
Turbina wodna miała osiem równomiernie rozmieszczonych łopatek. Ile stopni ma kąt
dwukrotnie większy od zaznaczonego na rysunku?
Zadanie 13. (0-1)
Podczas burzy Ania usłyszała uderzenie pioruna po upływie 3 sekund od chwili, gdy
zobaczyła błyskawicę. W jakiej odległości od Ani uderzył piorun, jeżeli szybkość
dźwięku w powietrzu wynosi 340 m/s ?
A. 113 m
B.340m
C.343 m
D. 1020m
Zadanie 14. (0-1)
Jeżeli tlen gwałtownie łączy się z pierwiastkiem i towarzyszy temu świecenie oraz
wydzielanie ciepła, to jest to reakcja
A. rozkładu.
B. spalania.
C. wymiany.
D. zobojętniania.
Zadanie 15. (0-1)
Michał, Adam i Krzyś mieszkają w trzech domach ustawionych tak jak na poniższym rysunku. Chłopcy
wyznaczyli w parku miejsce spotkań (S) w jednakowej odległości od każdego z domów. Przyjmując
oznaczenia: M - dom Michała, A - dom Adama, K- dom Krzysia, określ, czy miejsce „S" to punkt przecięcia
się
A. wysokości trójkąta MAK.
B. symetralnych boków trójkąta MAK.
C. dwusiecznych kątów trójkąta MAK.
D. środkowych trójkąta MAK.
Zadanie 16. (0-1)
W parku rosną drzewa iglaste i liściaste. Wszystkich drzew jest 186. Gdyby było
o 12 drzew iglastych więcej, to stanowiłyby one połowę drzew liściastych. Który
z układów opisuje treść zadania (x - liczba drzew iglastych, y - liczba drzew
liściastych)?
A.
B.
C.
D.
Zadanie 20. (0-1)
W jednej szyszce sosny znajduje się około 35 nasion. Do obsadzenia jednego ara szkółki
leśnej potrzeba sadzonek wysianych z 5000 nasion. Ile szyszek należy zebrać, aby obsadzić
1,5 ha szkółki leśnej (1 ha = 100 a)?
A. ok. 214500
B. ok. 21450
C. ok. 2145
D. ok. 215
Zadanie 21. (0-1)
Jedna duża sosna „produkuje" w ciągu doby 14,4 m3 tlenu. Człowiek zużywa 0,2 m3 tlenu na
godzinę. Na ile godzin wystarczy człowiekowi tlenu „wyprodukowanego" przez sosnę w ciągu
doby?
A. 2,88
B. 7,20
C.28,80
D. 72
Zadanie 24. (0-1)
Członkowie klubu wykonali kalendarz na rok przestępny (366 dni). Na każdy dzień
przeznaczyli jedną kartkę. Z jednego arkusza papieru wycinali pięć takich kartek. Ile arkuszy
papieru musieli kupić, aby powstał kalendarz?
A. 37
B.73
C. 74
D. 366
Zadanie 25. (0-1)
Oto dwie kartki z kalendarza:
O ile minut dzień 21 czerwca 2002 r. był dłuższy od 20 maja 2002 r.?
A. 9
B.17
C. 26
Zadanie 26. (0-3)
Żółte kwiaty berberysu zwyczajnego rosną w gronach składających się z jednego kwiatu
szczytowego i różnej liczby kwiatów bocznych. Każdy kwiat boczny ma po 6 płatków, zaś
kwiat szczytowy ma ich 5. Uzupełnij tabelkę przedstawiającą zależność liczby płatków od
liczby kwiatów w gronie.
9
n
Liczba wszystkich 7
kwiatów w gronie
Liczba płatków
w gronie
41
77
Zadanie 28. (0-3)
Na szkółkę leśną przeznaczono prostokątną działkę o powierzchni 300 m 2 i szerokości
15 metrów. Ile metrów siatki należałoby kupić na ogrodzenie tej szkółki, gdyby
długości boków zwiększono o 2 metry każdy? Zapisz obliczenia.
Zadanie 29. (0-2)
Wiewiórka może pokonać 90 metrów w 30 sekund, zaś kuna leśna przebywa 100
metrów w 25 sekund. Z jaką szybkością może poruszać się każde z wymienionych
zwierząt? Ile czasu potrzebuje wiewiórka na pokonanie 150 metrów? Zapisz obliczenia.
Zadanie 30. (0-3)
Uczniowie prowadzili obserwacje meteorologiczne. Wyniki obserwacji zapisali w tabeli:
Miesiące
III
IV
V
VI
VII
IX
VIII
3,6
7,9
Temp.
13,8
15,7
18,0
17,7
13,6
w°C
35
42
50
63
76
70
30
Opady
w mm
Na podstawie danych z powyższej tabeli oblicz
a.
średnią temperaturę obserwowanego okresu -
b.
amplitudę temperatury - .................................
c.
całkowity opad w obserwowanym okresie - ......
Zadanie 31. (0-3)
Prostopadłościenna piaskownica ma wymiary: 2 m; 2 m; 0,6 m. Ile metrów sześciennych
2
piasku należy dostarczyć, aby tę piaskownicę wypełnić w
jej wysokości?
3
Zapisz obliczenia.
Zadanie 32. (0-2)
Złoty pierścionek waży 3,5 g i wykonany został ze złota próby 750 (próba oznacza liczbę
gramów czystego złota w 1000 g wyrobu). Ile gramów czystego złota jest w tym
pierścionku? Zapisz obliczenia.
Zadanie 34. (0-4)
Klub Janka za zwycięstwo w regatach otrzymał nagrodę w wysokości 2000 zł. Nagrodę
tę członkowie klubu chcą ulokować w banku na okres jednego roku. Rozważane są dwie
oferty:
I - lokata na okres 12 miesięcy według stałej stopy procentowej w wysokości 8%
w stosunku rocznym,
II - lokata na okres pół roku oprocentowana według stałej stopy procentowej
w wysokości 4% w stosunku półrocznym. Po 6 miesiącach dopisywane są odsetki
i nowa kwota jest ulokowana ponownie na koncie o takim samym oprocentowaniu.
Oblicz kwotę odsetek przy każdej z proponowanych ofert. Zapisz obliczenia.
Na mapie zaznaczono 10 krajów, które przystąpiły do Unii Europejskiej 1 maja 2004 roku. Ich
powierzchnię podano w tys. km2. Wykorzystując te informacje rozwiąż zadania 1. i 2.
Zadanie 1. (0-1)
Jakim procentem powierzchni Węgier jest powierzchnia Cypru?
A. 0,1 %
B 1%
C. 9,3 %
D. 10 %
Zadanie 2. (0-1)
Powierzchnia najmniejszego z tych państw jest mniejsza od powierzchni największego
państwa około
A.
15 razy.
B.
1042 razy.
C.
30 razy.
D.
6 razy.
Zadanie 4. (0-1)
Logo Unii Europejskiej to figura złożona z 12 pięcioramiennych
gwiazd (rysunek obok). Figura ta ma
A. dokładnie 1 oś symetrii.
B. dokładnie 2 osie symetrii.
C. dokładnie 6 osi symetrii.
D. dokładnie 12 osi symetrii.
Zadanie 5. (0-1)
Punkty K, L, M, N, P są wierzchołkami pięciokąta foremnego. Punkt O jest
środkiem okręgu, do którego należą punkty K, L, M, N, P. Miara kąta a
zaznaczonego na rysunku jest równa
A. 30°
B. 36°
C. 72°
D. 45°
Na diagramie przedstawiono kurs sprzedaży euro pierwszego dnia każdego
z 12 miesięcy. Diagram wykorzystaj do rozwiązania zadań 6., 7. i 8.
Zadanie 6. (0-1)
Za 50 euro kupione w lipcu zapłacono
A.
220 zł
B.
202 zł
C.
201 zł
D.
210 zł
Zadanie 7. (0-1)
W którym miesiącu za 200 euro zapłacono 750 zł?
A. W styczniu.
B. W maju.
C. W czerwcu.
D. W lutym.
Zadanie 8. (0-1)
W maju za 540 zł kupiono
A. 140 euro.
B. 150 euro.
C. 160 euro.
D. 120 euro.
Zadanie 11. (0-1)
Traktat ustanawiający Unię Europejską wszedł w życie w XX wieku. Rok podpisania tego
traktatu jest liczbą czterocyfrową, której cyfra dziesiątek jest o 6 większa od cyfry jedności i
której suma cyfr jest równa 22. Zaznacz równanie, które odpowiada treści zadania, jeśli cyfrę
jedności oznaczymy przez x.
A.
x + x + 6 = 22
B. x-6 + x = 22
C. 10 + x-6 + x = 22
D. 10 + x + 6 + x = 22
Zadanie 14. (0-1)
Zasolenie Bałtyku u wybrzeży Danii wynosi średnio 1,7%. W 200 gramach wody
morskiej znajduje się około
A. 0,85 g soli.
B. 3,4 g soli.
C. 8,5 g soli.
D. 34 g soli.
Zadanie 25. (0-1)
Bilet normalny do Luwru kosztuje a euro, cena biletu ulgowego stanowi 75% ceny
biletu normalnego. Koszt zakupu biletów dla grupy, w której jest x osób dorosłych oraz
y uczniów uprawnionych do zakupu biletów ulgowych, można zapisać za pomocą
wyrażenia algebraicznego
A. ax + y*0,25a
B.
ax + 0,75y
C.
a(x + 0,75)
D. a(x + O,75y)
Zadanie 26. (0-4)
Na dziedzińcu przed Luwrem zbudowano szklaną piramidę. Piramida ta ma kształt
ostrosłupa prawidłowego czworokątnego o wysokości około 20 metrów i krawędzi
podstawy 30 metrów. Wykonaj rysunek pomocniczy wraz z oznaczeniami i oblicz
powierzchnię ścian bocznych szklanej piramidy. Zapisz obliczenia.
Zadanie 28. (0-3)
Oblicz wysokość Wieży Eiffla wykorzystując informacje
podane na rysunku.
Wynik podaj z dokładnością do setek metrów.
Zapisz obliczenia, przyjmując 3 =1,73.
Zadanie 34. (0-3)
Trzem laureatom ( I, II, III miejsce) Konkursu Wiedzy o Unii Europejskiej ufundowano
nagrody pieniężne. Nagroda II była o 20% mniejsza od I, a III stanowi 60% wartości I.
Na nagrody przeznaczono łącznie 120 euro. Oblicz, ile euro dostał każdy laureat tego
konkursu. Zapisz obliczenia.
Zadanie 8. (0-1)
Zawartość witaminy C w owocach głogu jest równa 1,5%. Ilość witaminy C w jednym
kilogramie owoców głogu wynosi
A. 0,15 g
B. 1,50 g
C. 15,0 g
D. 150 g
Zadanie 9. (0-1)
Oddziaływanie między borowikami a sosnami polega na
A.
czerpaniu obopólnych korzyści.
B.
rywalizacji o te same zasoby środowiska.
C.
czerpaniu korzyści przez grzyby bez szkodzenia drzewom.
D.
pobieraniu przez grzyby substancji odżywczych z jednoczesnym osłabianiem drzew.
Informacja do zadań 10. i 11.
W czasie snu zdrowy człowiek, średniego wzrostu i ciężaru ciała, zużywa około 1800 kcal na
dobę. Tabela ilustruje zmiany dobowego zapotrzebowania na energię ludzi różnych zawodów.
Zawód
Dobowe zużycie energii w stosunku do
1800 kcal
Krawiec
149%
Mechanik
177%
Stolarz
181%
Zadanie 10. (0-1)
Zużycie energii w czasie doby przez osobę pracującą w zawodzie mechanika jest równe
A. 3186 kcal
B. 1977 kcal
C. 1623 kcal
D. 177 kcal
Zadanie 11. (0-1)
O ile kilokalorii więcej zużyje organizm człowieka pracującego w zawodzie stolarza niż
krawca?
A. 32 kcal
B. 72 kcal
C. 330 kcal
D. 576 kcal
Informacja do zadań 12. i 13.
Podczas remontu łazienki glazurnik planuje wyłożyć podłogę terakotą. Podłoga ma wymiary
2,4 m x 2,7 m. Na straty należy doliczyć 10% terakoty.
Zadanie 12. (0-1)
Jaką najmniejszą liczbę pełnych m2 terakoty należy zakupić, aby nie zabrakło jej do
wyłożenia podłogi?
A. 7m2
B. 8m2
C. 11m2
D. 12 m2
Zadanie 13. (0-1)
Płytka terakoty ma kształt kwadratu o boku 30 cm. Ile dokładnie sztuk płytek potrzeba
byłoby do wyłożenia podłogi, gdyby nie było żadnych strat?
A. 17
B. 34
C. 72
D. 216
Informacja do zadań 16. i 17.
Kuba wybiera się na wakacyjną wycieczkę, której koszt ma wynosić 285 złotych. Uzbierał już
120 zł i co miesiąc odkłada po 15 zł.
Zadanie 17. (0-1)
Ile minimalnie miesięcy oszczędzania wystarczy, aby Kuba zebrał kwotę potrzebną na
wyjazd?
A. 13
B. 12
C.11
D. 10
Zadanie 18. (0-1)
Jaką część doby stanowi czas wolny?
A. 1/12
B. 1/8
C. 1/6
D.1/3
Zadanie 19. (0-1)
Z powyższego diagramu wynika, że
A.
Kuba przeznacza na sen 30% doby.
B.
Kuba spędza w szkole trzecią część doby.
C.
dojazdy zajmują Kubie dwunastą część doby.
D.
zajęcia szkolne trwają o 25% krócej niż sen.
Zadanie 20. (0-1)
Stosunek czasu trwania zajęć pozalekcyjnych do czasu trwania zajęć szkolnych jest
równy
A. 3 : 0,5
B. 6 : 1,5
C. 0,5 : 3
D. 1,5 :6
Zadanie 28. (0-3)
Na spacerze w parku Ania zmierzyła, że jej cień jest o 20 cm dłuższy niż cień jej
młodszej siostry. Ania ma 160 cm wzrostu, a jej siostra jest o 10 cm niższa. Jakie
długości miały cienie obu dziewczynek? Zapisz obliczenia.
Zadanie 29. (0-4)
Przekątna ekranu telewizora ma 28 cali, czyli około 70 cm, gdyż 1 cal ~ 2,5 cm. Oblicz,
ile cali ma przekątna ekranu, który jest prostokątem o wymiarach 28 cm x 21 cm.
Zapisz obliczenia.
Zadanie 31. (0-3)
Wykres przedstawia, jak poruszał się pociąg osobowy rozpędzający się do uzyskania
ustalonej prędkości.
0
50
Oblicz drogę, na której pociąg przyspieszał. Zapisz obliczenia.
Ile dwudziestokilogramowych worków wapna palonego powinien zakupić murarz, aby
uzyskać z niego 148 kg wapna gaszonego? Zapisz obliczenia. (Masa atomowa Ca jest równa
40 u, O - 16 u, H - 1 u).
Zadanie 33. (0-5)
Dach domu pana Kowalskiego ma kształt
i wymiary figury przedstawionej na rysunku.
Pan Kowalski przeznaczył 2800 złotych na
zakup dachówki ceramicznej do pokrycia
całego dachu.
Hurtownia oferuje dachówki w dwóch gatunkach: I - 3 zł (brutto) za sztukę i II gatunek
- 2,70 zł (brutto) za sztukę. Ile najwięcej sztuk dachówek I gatunku może zakupić pan
Kowalski, jeżeli 10 dachówek wystarcza na pokrycie 1 m2 dachu? Zapisz obliczenia.
Zadanie 4. (0-1)
Można przyjąć, że parki narodowe w Polsce zajmują 3 105 ha, a powierzchnia Polski wynosi
3 107 ha. Podaj, ile razy powierzchnia zajmowana przez parki narodowe jest mniejsza od
powierzchni Polski.
A.
1000 razy
B.
10 razy
C.
30 razy
D.
100 razy
Zadanie 5. (0-1)
Leśnik powiększył dwukrotnie herb Pienińskiego Parku Narodowego. Wybierz
przekształcenie geometryczne, które mógł w tym celu wykorzystać.
A. symetria środkowa
B. symetria osiowa
C. jednokładność
D. nie ma takiego przekształcenia
Zadanie 7. (0-1)
Polacy kupują wody mineralne pochodzące z naturalnych źródeł. Oblicz średnią
arytmetyczną sprzedaży wód przedstawionych na diagramie.
A. 50 tys. litrów
B. 100 tys. litrów
C. 150 tys. litrów
D. 200 tys. litrów
Zadanie 10. (0-1)
Wybierz informację, którą można odczytać z wykresu przedstawiającego zależność
wysokości od czasu dla lecącego balonu.
A. Czasy pokonywania drogi dla krzywych AB, BC, CD są jednakowe.
B. Krzywa BC przedstawia ruch jednostajny balonu, AB - opadanie balonu.
C. Krzywa AB przedstawia wznoszenie, a CD - opadanie balonu.
D. Krzywa BC przedstawia wzrost wysokości balonu nad powierzchnią ziemi.
Zadanie 13. (0-1)
W Moskwie znajduje się jeden z większych placów świata. Ma on kształt prostokąta
o bokach: 400 m i 150 m. Pewnego dnia plac pokryła warstwa śniegu o wysokości 0,2 m.
Podaj objętość tego śniegu.
A. 1200 m3
B. 2400 m3
C.6000 m3
D.12000 m3
Zadanie 14. (0-1)
W niektórych krajach europejskich jednostką długości będącą nadal w użyciu jest stopa.
Zależność metra od stopy określa wzór: y = 0,3•x, gdzie y oznacza długość w metrach,
a x oznacza długość w stopach. Podaj w stopach wysokość dziewięciometrowej latarni
morskiej.
A. 2,7
B. 20
C. 27
D. 30
Zadanie 20. (0-1)
Statua Wolności jest wyższa o 38 metrów od Krzywej Wieży w Pizie. Suma liczb
wyrażających wysokości tych budowli (w metrach) wynosi 146. Przez x oznaczono
wysokość Statui Wolności w metrach, a przez y - wysokość Krzywej Wieży w metrach.
Zaznacz układ równań, który pozwoli na obliczenie wysokości tych budowli.
A.
B.
C.
D.
Zadanie 23. (0-1)
Podczas spaceru po lesie turysta zauważył wiewiórkę, która w sześciu równych skokach
pokonała drogę o szerokości 5,3 m. Podaj z dokładnością do jednego miejsca po
przecinku średnią długość pojedynczego skoku wiewiórki.
A.
0,7 m
B.
0,8 m
C.
0,9 m
D.
1,0 m
Zadanie 29. (0-3)
Turysta wypoczywał w domu rybaka. Dom ten znajduje się w miejscu, któremu na
rysunku odpowiada punkt o współrzędnych (2, -1). Zaznacz w układzie
współrzędnych położenie domu rybaka i podaj odległość domu rybaka od latarni
znajdującej się w punkcie L. Zapisz kolejne obliczenia.
Zadanie 30. (0-3)
Oblicz, które z przedstawionych na rysunku zwierząt ma w rzeczywistości większą
długość ciała. Zapisz obliczenia.
Zadanie 31. (0-4)
Palma o wysokości a [metrów] stoi obok piramidy w kształcie ostrosłupa o objętości
1200 m 3 . Korzystając z danych na rysunku, oblicz wysokość piramidy oraz pole jej
podstawy. Zapisz obliczenia.
Zadanie 32. (0-2)
Atrakcją turystyczną Kairu są bardzo wąskie uliczki. Układ kilku z nich przedstawiono
na rysunku. Ulica Cheopsa jest prostopadła do ulicy Sfinksa. Odległość lotniska
od kościoła jest taka sama jak odległość lotniska od fabryki. Oblicz miarę zaznac zonego
kąta a, pod którym przecinają się ulica Sfinksa i ulica Kleopatry. Zapisz obliczenia.
Zadanie 5. (0-1)
Średnia temperatura powietrza od poniedziałku do środy wynosiła 15 °C. Natomiast
od tego samego poniedziałku do czwartku 17 °C. Jaka była temperatura w czwartek?
A. 17 0C
B. 19°C
C. 20 °C
D. 23 °C
Informacja do zadań 15 - 17.
Powierzchnia upraw i zbiory herbaty w wybranych krajach.
Powierzchnia Zbiory
w tys. ha
w tys. ton
na jednego mieszkańca w kg
m
n
P
Świat
2331
2734
0,5
Chiny
900
633
0,5
Indie
440
785
0,8
Sri Lanka
188
277
14,9
Kenia
110
221
6,7
Indonezja
117
162
0,8
Turcja
77
121
1,9
Zadanie 15. (0-1)
Który kraj jest największym producentem herbaty?
A. Chiny.
B. Indie.
C. Sri Lanka.
D. Turcja.
Zadanie 16. (0-1)
Jaki jest udział procentowy herbaty indyjskiej w zbiorach światowych?
A.28,7%
B.22,1%
C. 18,9%
D. 8,1%
Zadanie 17. (0-1)
Ile hektarów zajmują plantacje herbaty w krajach innych niż wymienione w tabeli?
A. 499 000 ha
B. 599 000 ha
C. 1 499 000 ha
D. 1 599 000 ha
Zadanie 26. (0-2)
Do 200 g herbaty dodano łyżeczkę cukru (3 g). Oblicz stężenie procentowe otrzymanego
roztworu.
Zadanie 27. (0-3)
Jaką długość powinna mieć łyżeczka, aby - przy takim ułożeniu jak na rysunku
wystawała z kubka około 3 cm?
Zadanie 32. (0-5)
Masz 3 kubki o wymiarach zewnętrznych: wysokość 10 cm, średnica dolna 6 cm,
średnica górna 8 cm.
Zaprojektuj otwarte prostopadłościenne pudełko (bez przykrycia) tak, aby zmieścić
w nim te trzy kubki. Przy pakowaniu nie można wkładać kubka w kubek.
Wskazówka. Najpierw ustal możliwie najmniejsze wymiary pudełka (odpowiednio
ustawiając kubki) i wpisz je na modelu.
Następnie narysuj siatkę pudełka w skali 1:4 i podaj wymiary siatki w skali.
Oblicz, ile cm2 papieru trzeba zużyć na wykle enie wnętrza zaprojektowanego pudełka.
Informacje do zadań 1., 2., 3., 4. i 5.
Uczniowie klas trzecich pewnego gimnazjum urządzili w swoich salach wystawy
przedstawiające najciekawsze miejsca w różnych krajach. Po obejrzeniu wszystkich
ekspozycji przeprowadzona została ankieta, w której uczniowie odpowiadali na pytanie, który
kraj chcieliby odwiedzić. Każdy z ankietowanych mógł wybrać tylko jeden kraj.
Oto jakich wyborów dokonali uczniowie.
Zadanie 1. (0 - 1)
Ilu uczniów uczestniczyło w ankiecie?
A. 310
B. 300
C. 290
D. 250
Zadanie 3. (0 - 1)
Jaki procent liczby uczniów wybierających Indie stanowiła liczba uczniów, którzy
wybrali Egipt?
A. 150%
B. 662%
C. 60%
D. 40%
Zadanie 4. (0 - 1) Wskaż
zdanie prawdziwe.
A.
Liczba uczniów, którzy wybrali Australię jest o połowę mniejsza od liczby uczniów,
którzy wybrali USA.
B.
Liczba uczniów, którzy wybrali Indie, jest czterokrotnie większa niż liczba uczniów,
którzy wybrali kraje europejskie.
C.
Liczba uczniów, którzy wybrali kraje europejskie, jest o połowę większa niż liczba
uczniów, którzy wybrali Australię lub Egipt.
D.
Liczba uczniów, którzy wybrali Włochy lub Indie, jest taka sama jak liczba uczniów,
którzy wybrali Japonię lub Egipt.
Zadanie 6. (0 - 1)
Przedstawiona na rysunku flaga Wielkiej Brytanii
A.
ma cztery osie symetrii i środek symetrii.
B.
ma cztery osie symetrii i nie ma środka symetrii.
C.
ma dwie osie symetrii i środek symetrii.
D.
ma dwie osie symetrii i nie ma środka symetrii.
Zadanie 11. (0-1)
Wykres przedstawia zależność drogi (S) przebytej przez autobus wycieczkowy od czasu
jazdy autobusu (t).
Analizując przedstawiony wykres można stwierdzić, że prędkość autobusu
A.
najpierw rosła, potem wynosiła zero.
B.
najpierw rosła, potem malała.
C.
najpierw rosła, potem była stała.
D.
najpierw była stała, potem wynosiła zero.
Informacje do zadań 12. i 13.
W czasie wycieczki do Berlina kilku uczniów weszło do pizzerii. Postanowili kupić jedną
dużą pizzę i podzielić ją między siebie na równe kawałki. Wykres przedstawia zależność
między kosztem (y), jaki musi ponieść każdy uczeń za jeden kawałek pizzy, a liczbą (x)
kupujących i dzielących pizzę.
Zadanie 12. (0 - 1)
Wskaż zapis algebraiczny zależności przedstawionej na wykresie.
A. y = 4x
B.y=4
X
C. xy = 0,4D.
Zadanie 13. (0 - 1)
Ile musiałby zapłacić za jeden kawałek pizzy każdy z ośmiu kupujących tę pizzę?
A. 0,5 euro
B. 1,6 euro
C. 4 euro
D. 8 euro
Zadanie 14. (0 - 1)
Uczniowie oglądali makietę Alp - najwyższych gór Europy. Znaleźli na niej najwyższy szczyt
Austrii - Grossglockner (3797 m n.p.m.) i najwyższy szczyt Europy - Mont Blanc (4807 m
n.p.m.). Wysokość względna Mont Blanc w stosunku do Grossglockner wynosi
A 1010 m n.p.m.
. 1010 m
C. 4807 m n.p.m
D. 8604 m
Zadanie 15. (0 - 1)
Na obszarze Alp panują odmienne warunki klimatyczne niż na nizinach. Wskaż cechy
klimatu wysokogórskiego.
A. Spadek temperatury i ciśnienia powietrza wraz ze wzrostem wysokości, duże sumy
opadów, silne wiatry.
B. Spadek temperatury i ciśnienia powietrza wraz ze wzrostem wysokości, długie zimy, małe
sumy opadów.
C. Długa zima, spadek temperatury i wzrost ciśnienia powietrza wraz ze wzrostem
wysokości, małe sumy opadów.
D. Silne wiatry, wzrost temperatury i spadek ciśnienia powietrza wraz ze wzrostem
wysokości, duże sumy opadów.
Zadanie 16. (0 - 1)
W Londynie ogromnym problemem jest smog, składający się między innymi z tlenków
siarki i tlenków azotu. Pewnego dnia w atmosferze znalazła się taka sama masa tlenków
siarki co tlenków azotu. Diagramy przedstawiają źródła zanieczyszczeń powietrza tymi
tlenkami.
Największa łączna masa wyemitowanych tlenków azotu i tlenków siarki pochodziła z
A.
transportu.
B.
gospodarstw domowych.
C.
energetyki.
D.
przemysłu (w tym rafinerii).
Zadanie 17. (0 - 1)
Badano odczyn próbek wody pobranych z różnych źródeł, używając jako wskaźnika
oranżu metylowego. Jedną z próbek stanowiła woda z kwaśnych opadów zebrana w
Londynie. Doświadczenie przebiegało według schematu
próbka wody + oranż metylowy -^ roztwór
zlewka I
zlewka II
zlewka III
Woda zebrana w Londynie mogła znajdować się
A. w zlewce I.
.B. w zlewce II.
C. w zlewce III.
D. we wszystkich zlewkach.
Zadanie 18. (0 - 1)
Wskaż zestaw, który zawiera wyłącznie wzory sumaryczne soli.
A. NaCl, MgSO4 , CaCl2, HNO3 C.
B. NaCl, CaSO4 , CaCl2, Al(OH)3
NaCl, Ca(OH)2, HCl, Mg3(PO4)2
D. NaCl, KNO3,MgSO4 , CaSO4
Zadanie 19. (0 - 1)
Wskaż reakcję zobojętniania.
A. 2Na + H2SO4 —> Na2SO4 + H2 C.
Na2O + H2SO4— > Na2SO4 + H2O
Informacje do zadań 20. i 21.
Porosty to organizmy bardzo wrażliwe na zanieczyszczenia powietrza dwutlenkiem siarki
(SO2). Z tego powodu uznano je za organizmy wskaźnikowe określające stopień
zanieczyszczenia atmosfery. Poniższa tabela przedstawia VII-stopniową skalę porostową.
Strefa I
Strefa I
Strefa II
Strefa IV
Strefa V
Strefa VI
Strefa VII
powietrze
szczególnie
silnie
zanieczyszczone
Ponad 170
mg SO2/m3
kora drzew
bez porostów
powietrze powietrze powietrze powietrze powietrze
bardzo silnie
silnie
średnio
mało
nieznacznie
zanieczysz- zanieczysz- zanieczysz- zanieczysz - zanieczyszczone
czone
czone
czone
czone
powietrze
czyste
170-125 mg 125-70 mg
SO2/m3
SO2/m3
misecznica złotorost
proszkowata ścienny
40-30 mg
SO2/m3
granicznik
płucnik
70-60 mg
SO2/m3
mąkl a
tarniowa
Strona 8 z 15
60-50 mg
SO2/m3
mąklik
otrębiasty
50-40 mg
SO2/m3
brodaczka
nadobna
Zadanie 20. (0 - 1)
Jeżeli w londyńskim parku skażenie powietrza wynosi 85 mg SO2/m3, to
A.
powietrze jest średnio zanieczyszczone, a porostem wskaźnikowym jest mąklik
otrębiasty.
B.
powietrze jest średnio zanieczyszczone, a porostem wskaźnikowym jest złotorost
ścienny.
C.
powietrze jest silnie zanieczyszczone, a porostem wskaźnikowym jest mąkla tarniowa.
D.
powietrze jest silnie zanieczyszczone, a porostem wskaźnikowym jest złotorost
ścienny.
Zadanie 21. (0 - 1)
W parku, w którym na drzewach dominował złotorost ścienny, po pięciu latach
zaobserwowano dominowanie mąklika otrębiastego. Oznacza to, że w tym czasie
zanieczyszczenie powietrza dwutlenkiem siarki (SO2) na tym obszarze
A.
wzrosło i powietrze jest mało zanieczyszczone.
B.
zmalało i powietrze jest mało zanieczyszczone.
C.
zmalało i powietrze jest średnio zanieczyszczone.
D.
wzrosło i powietrze jest średnio zanieczyszczone.
Zadanie 22. (0 - 1)
Porosty to organizmy powstające w wyniku symbiozy
B. grzyba i drzewa.
A. grzyba i glonu.
D. dwóch gatunków grzybów.
C. grzyba i mchu.
Zadanie 23. (0 - 1)
Na obszarze pewnego parku rośnie 180 drzew, a stosunek liczby drzew do liczby
krzewów wynosi 3:5. Liczba krzewów w tym parku wynosi
C. 300
A. 108
B. 288
D. 480
Zadanie 24. (0 -1)
Tabela przedstawia zawartość glukozy w osoczu krwi czterech pacjentów na czczo oraz
normę fizjologiczną.
norma
wynik I
wynik II wynik III wynik IV
fizjologiczna pacjenta
pacjenta
pacjenta
pacjenta
49
55
98
135
Zawartość glukozy 55-100
w osoczu krwi mg
100 ml
Na cukrzycę choruje prawdopodobnie pacjent
B. I
B. II
C. III
D. IV
Zadanie 25. (0 - 1)
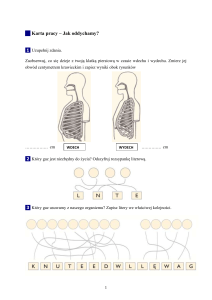
Rysunek przedstawia schemat budowy układu oddechowego człowieka.
Wskaż prawidłowy opis zaznaczonych elementów schematu.
A. 1 - tchawica, 2 - krtań, 3 - oskrzela;
B. 1 - krtań, 2 - tchawica, 3 - oskrzela;
C.1- krtań, 2 - oskrzela, 3 - tchawica;
D. 1- tchawica, 2 - oskrzela, 3 - krtań.
Zadanie 26. (0 - 3)
Zwiedzając wystawy państw, uczniowie rozpoznawali występujące w tych krajach
w stanie naturalnym rośliny i zwierzęta. Spośród podanych przykładów flory i fauny
wybierz te, które występują w formacji roślinnej wymienionych w tabeli państw
i uzupełnij tabelę.
buk, leniwiec, niedźwiedź grizli, palma daktylowa, renifer, sarna, świerk, wielbłąd
państwo i formacja roślinna flora
fauna
Szwecja-tajga
Niemcy - lasy liściaste
Egipt - pustynia
Zadanie 27. (0 - 3)
Uzupełnij tabelę, przyporządkowując nazwy państw do odpowiedniego położenia
geograficznego.
Austria, Indie, Japonia, Szwecja, Wielka Brytania, Włochy
położenie geograficzne
nazwa państwa
wyspiarskie
na półwyspie
śródlądowe
Informacje do zadania 28.
Uczniowie klasy III b zwiedzali Brukselę. Miejscem rozpoczęcia wycieczki była Starówka.
Idąc równym tempem, w ciągu jednej godziny przeszli 3 km. Przez pół godziny odpoczywali,
po czym ruszyli w dalszą drogę, idąc cały czas równym tempem. Po następnych dwóch
godzinach okazało się, że podczas całej wycieczki pokonali drogę 9 km.
Zadanie 28. (0 - 2)
Opisz osie układu współrzędnych i sporządź wykres przedstawiający długość drogi
przebytej przez uczestników wycieczki w zależności od czasu trwania wycieczki.
Zadanie 29. (0 - 4)
Na wycieczkę do Brukseli pojechało 38 uczniów i 4 opiekunów. Zarezerwowano dla nich
nocleg w pokojach dwu i trzyosobowych. Cała grupa nocowała w 17 pokojach.
Wszystkie zarezerwowane pokoje były w pełni wykorzystane. Ile zarezerwowano pokoi
dwuosobowych, a ile trzyosobowych? Zapisz obliczenia.
Zadanie 30. (0 - 5)
Podłoga w pokojach, w których nocowali uczniowie, ułożona była z płytek w romby
(patrz rysunek).
Stosunek długości przekątnych jednej płytki (rombu) wynosi 3 : 4, a bok płytki ma
długość 20 cm. Oblicz pole powierzchni takiej płytki. Zapisz obliczenia.
Zadanie 31. (0 - 2)
Zwiedzanie Brukse
godzina czasu słonecznego była wówczas w Warszawie (52°N, 21°E)? Zapisz obliczenia.
Zadanie 32. (0 - 3)
Aby zaparzyć herbatę, Tomek chce użyć czajnika elektrycznego o mocy 2 kW. Cz y może
go włączyć, jeżeli instalację elektryczną zabezpieczono bezpiecznikiem 20A i włączono
już żarówkę o mocy 100 W, żarówkę o mocy 60 W oraz kuchenkę mikrofalową o mocy
1,5 kW. Przyjmij napięcie w instalacji elektrycznej 230 V. Zapisz obliczenia.
Zadanie 33 (0 - 3)
Tomek wykonał doświadczenie, w którym na cynk podziałał kwasem solnym. Probówkę
do zbierania wydzielającego się gazu umieścił w wanience z wodą. Rysunek przedstawia
schemat tego doświadczenia.
1. Zapisz równanie reakcji zachodzącej w doświadczeniu.
2. Nazwij powstałe produkty reakcji, uzupełniając zdanie:
Produktami reakcji zachodzącej w doświadczeniu są....................
3. Napisz, w jaki sposób zidentyfikujesz wydzielający się gaz.
Brudnopis:
Informacje do zadań 1-3.
Echo powstaje wtedy, gdy fale głosowe padają prostopadle na możliwie gładką
pionową ścianę i odbijają się od niej w kierunku źródła głosu. Odległość źródła głosu
od ściany musi przy tym być co najmniej 17 m, wtedy bowiem droga głosu tam i z powrotem
wynosi 34 m i głos przebywa ją w czasie 0,1 s; jest to najkrótszy odstęp czasu, w którym ucho
może odróżnić głośno wypowiedzianą sylabę od jej powtórzenia przez echo. (...)
Dwusylabowe echo powstaje przy odległości ściany 34 m, trój sylabowe przy
odległości 51 m itd.; echo dwukrotne powstanie wtedy, gdy wywołana sylaba ulegnie odbiciu
od dwóch różnych ścian, znajdujących się w różnych odległościach. W ten sposób można
w sprzyjających okolicznościach (np. w górach) usłyszeć echo trzykrotne dwusylabowe.
Mała encyklopedia przyrodnicza, PWN, Warszawa, 1962
Zadanie 1. (0-1)
Jaką szybkość rozchodzenia się dźwięku w powietrzu przyjęli autorzy notatki?
A. 3 4 m
B. 170 m
C .330 m
D.340 m
s
s
Zadanie 2. (0-1)
Jeśli krzykniemy w stronę ściany oddalonej o 9 metrów, to
A. fale głosowe nie odbiją się od ściany.
B. usłyszymy echo po 0,05 s.
C. nie usłyszymy echa.
D. usłyszymy echo dwukrotne.
Zadanie 3. (0-1)
W jakiej co najmniej odległości od ściany trzeba krzyknąć, aby mogło powstać echo
czterosylabowe?
A. 17 m
B. 34 m
C. 51 m
D. 68 m
Zadanie 4. (0-1)
Nietoperz wysyła fale ultradźwiękowe o różnych długościach. Jedna z nich ma
w powietrzu długość około 3,4 mm i szybkość 340 m/s. Korzystając z zależności v = X ■ f
(gdzie v oznacza szybkość fali a X i fodpowiednio jej długość i częstotliwość), oblicz
częstotliwość tej fali.
A. 0,0001 kHz
B. 100 kHz
C. 336,6 kHz
D. 1156 kHz
Informacje do zadań 5. i 6.
Budowa ucha
A.
B.
C.
D.
Zadanie 5. (0-1)
W której części ucha znajdują się kosteczki słuchowe?
A. W uchu wewnętrznym.
B. W uchu środkowym.
C. W uchu zewnętrznym.
D. W małżowinie usznej.
Zadanie 6. (0-1)
W procesie słyszenia biorą udział kolejno:
błona bębenkowa, kosteczki słuchowe, płyn zawarty w ślimaku, komórki czuciowe, nerw
słuchowy, ośrodek słuchowy w mózgu.
błona bębenkowa, kanały półkoliste, kosteczki słuchowe, nerw słuchowy, ośrodek
słuchowy w mózgu.
ośrodek słuchowy w mózgu, nerw słuchowy, błona bębenkowa, kosteczki słuchowe,
ślimak, trąbka Eustachiusza.
trąbka Eustachiusza, kanały półkoliste, błona bębenkowa, kosteczki słuchowe, ośrodek
słuchowy w mózgu.
Zadanie 7. (0-1)
Impuls dźwiękowy jest przekazywany z ucha wewnętrznego do mózgu jako
A. fala akustyczna.
B. bodziec mechaniczny.
C. impuls elektryczny.
D. drgania nerwów słuchowych.
Zadanie 8. (0-1)
Wyniki badania krwi Agnieszki
badany czynnik
wynik Agnieszki
norma
liczba krwinek czerwonych
4,2 x 1012 /l
4,0-4,4 xio 12 /l
liczba krwinek białych
26,0 x 109 /l
4,0 - 10,0 x 109 /l
9
liczba płytek krwi
220 x 10 /l
200-300 xio 9 /l
OB po jednej godzinie
20 mm
do 12 mm
czas krwawienia
6 minut
do 7 minut
Po odczytaniu takich wyników lekarz pierwszego kontaktu zapewne
A. zleci kolejne badania w kierunku sprawdzenia przyczyny małopłytkowości, która może
powodować zaburzenia krzepliwości krwi.
B. przeprowadzi z Agnieszką dokładny wywiad i zleci dalsze badania w kierunku wykrycia
utajonego stanu zapalnego.
C. zleci dalsze badania w kierunku wykrycia przyczyn anemii (niedokrwistości).
D. stwierdzi, że wyniki badań Agnieszki są w normie.
Zadanie 9. (0-1)
Wiosną, w obawie przed awitaminozą, Agnieszka zmieniła dietę na roślinną z dużym
udziałem jarzyn, które właśnie zaczęły wyrastać w jej ogródku. Aby ustrzec się przed
niedoborami wapnia, spowodowanymi wiązaniem wapnia przez jony kwasu
szczawiowego zawartego w jarzynach, powinna jeść również więcej produktów bogatych
w wapń, mianowicie:
A. mleka i serów.
B. miodu i kakao.
C. tranu i mięsa.
D. szpinaku i sałaty.
Zadanie 10. (0-1)
Rysunek przedstawia wzór strukturalny szczawianu wapnia.
Informacje do zadań 13. i 14.
Głównym składnikiem kredy jest węglan wapnia CaCO3. Jego rozkład wymaga wysokiej
temperatury i przebiega według schematu:
CaCO3
temperatura
CaO + CO 2
Zadanie 13. (0-1)
Oblicz, ile dwutlenku węgla powstało w takiej reakcji, jeżeli ze 100 g CaCO3 otrzymano
56 g CaO.
A. 156 g
B.100g
C. 56 g
D. 44 g
Zadanie 14. (0-1)
Uczniowie wykonali dwa doświadczenia z kredą:
Doświadczenie I:
kawałek kredy włożono do wody z dodatkiem fenoloftaleiny.
Obserwacje: nie zaobserwowano zmian. Doświadczenie II:
kawałek
kredy ogrzano w płomieniu palnika i następnie
włożono do wody z dodatkiem fenoloftaleiny. Obserwacje: ogrzana
część kredy zabarwiła się na kolor malinowy.
O czym świadczy zabarwienie się podgrzanej części kredy?
A. Wzrosła temperatura wody.
B. Obniżyła się temperatura kredy.
C. Tlenek wapnia zareagował z wodą.
D. Dwutlenek węgla rozpuścił się w wodzie.
Informacje do zadań 15 - 18.
Na mapie zaznaczono granice pasów krajobrazowych w Polsce oraz położenie czterech miast:
Lublina, Olsztyna, Szczecina i Wrocławia.
Zadanie 15. (0-1)
Które miasto leży w tym samym pasie krajobrazowym co punkt o współrzędnych
53°N, 21°E?
A. Lublin
B. Olsztyn
C. Szczecin
D. Wrocław
Zadanie 16. (0-1)
Warta jest trzecią co do długości rzeką w Polsce (808 km) i przepływa przez trzy pasy
krajobrazowe:
A. pas wyżyn, pas nizin środkowopolskich, pas pojezierzy.
B. pas młodych gór, pas wyżyn, pas nizin środkowopolskich.
C. pas nizin środkowopolskich, pas pojezierzy, pas nizin nadmorskich.
D. pas wyżyn, pas młodych gór, pas pojezierzy.
Zadanie 17. (0-1)
W którym z miast zaznaczonych na mapie Słońce góruje najwcześniej?
B. W Olsztynie.
C. W Szczecinie.
D. We Wrocławiu.
Zadanie 18. (0-1)
Łuk południka, któremu odpowiada 1°, ma długość równą 111 km. Długość łuku
południka 19°E na terenie Polski to
A. mniej niż 3 - 1 1 1 km.
B. około 19-111 km.
C. około 5 • 111 km.
D. więcej niż 6 - 1 1 1 km.
Informacje do zadań 19-23.
Na polski rynek wprowadzono w 2002 roku 2,5 miliona ton opakowań. Czwartą część
zużytych opakowań poddano recyklingowi - informuje Ministerstwo Środowiska.
ILE W POLSCE ODZYSKUJEMY
Rodzaj opakowań
Poziom recyklingu (w procentach)
tworzywa sztuczne
aluminium
blacha
papier i tektura
szkło
materiały naturalne
tworzywa
wielomateriałowe
wymagany w Polsce
w 2002 r.
7
15
6
37
13
5
5
uzyskany w Polsce w
2002 r.
11,4
22,8
16,4
44,4
15,0
22,6
6,5
wymagany w
2007 r.
25
40
20
48
40
15
25
Ministerstwo Środowiska (za „Gazetą Wyborczą" 17.10.03)
Zadanie 19. (0-1)
W 2002 r. poddano recyklingowi więcej niż czwartą część zużytych opakowań z
A. tworzyw wielomateriałowych.
B. szkła.
C. papieru i tektury.
D. aluminium.
Zadanie 20. (0-1)
W 2002 r. osiągnięto wyższy niż będzie wymagany w 2007 r. poziom recyklingu
A. tworzyw sztucznych.
B. materiałów naturalnych.
C. papieru i tektury.
D. blachy.
Zadanie 21. (0-1)
Różnica między poziomem recyklingu wymaganym w 2002 roku i poziomem recyklingu
wymaganym w 2007 roku jest największa dla
A. tworzyw wielomateriałowych.
B. blachy.
C. szkła.
D. materiałów naturalnych.
Zadanie 22. (0-1)
Ile tysięcy ton szklanych opakowań poddano recyklingowi w 2002 r?
A. 13
B. 15
C. 375
D. Za mało danych by odpowiedzieć.
Zadanie 23. (0-1)
Wymagany w 2007 r. poziom recyklingu tworzyw sztucznych można osiągnąć bez
zwiększania masy odzyskanych opakowań (zmieniając za to masę zużywanych
opakowań). Jaka musiałaby być wtedy, w porównaniu z 2002 r., masa zużytych w ciągu
roku opakowań z tworzyw sztucznych?
A. Ponad dwa razy mniejsza.
B. Mni ej sza o j edną czwartą.
C. Większa o 13,6%.
D. Większaojednączwartą.
Zadanie 24. (0-1)
Który rysunek jest symbolem recyklingu?
2.
4.
A. 1.
B. 2.
C. 3.
Zadanie 25. (0-1)
Który z powyższych symboli ma środek symetrii?
A. 2.
B.
C. 4.
D. 4.
D. Żaden.
Informacje do zadań
26-28.
Klasa IIIa
postanowiła wziąć
udział w zbiórce
zużytych baterii
elektrycznych.
Rezultaty
pierwszego tygodnia zbierania baterii przedstawia diagram.
0 1 2 3 4 5 6 7 8 9
10 Liczba baterii
Zadanie 26. (0-2)
Uzupełnij zdania:
Żadnej baterii nie przyniosło ............. uczniów. Największą liczbą baterii przyniesionych
przez jednego ucznia jest ................ Najczęściej uczniowie przynosili po ............... baterii.
Zadanie 27. (0-2)
Oblicz, ile baterii zebrali uczniowie klasy IIIa w pierwszym tygodniu. Napisz obliczenia.
Zadanie 28. (0-4)
Oblicz, ile procent uczniów tej klasy przyniosło co najmniej jedną baterię. Napisz
obliczenia.
Zadanie 29. (0-1)
Po miesiącu zbierania baterii klasa IIIc miała ich 2 razy więcej niż klasa IIIb, a klasa
IIIb o 30 baterii mniej niż klasa IIIa. Razem te trzy klasy zebrały 750 baterii. Oznacz
liczbę baterii zebranych przez klasę IIIa przez x i ułóż równanie odpowiadające treści
zadania.
Odpowiedź: .................................................................................................................................
Zadanie 30. (0-3)
Miedziany pręt o długości 1 m po ogrzaniu o 1°C wydłuży się o 0,0000165 m.
Wydłużenie jest wprost proporcjonalne do długości pręta i do przyrostu temperatury.
Oblicz, o ile centymetrów wydłuży się drut miedziany o długości 50 m przy ogrzaniu
o 30°C. Napisz obliczenia. Wynik podaj z dokładnością do dziesiątych części centymetra.
Zadanie 31. (0-4)
Pan Jan musi doprowadzić energię elektryczną do swojego placu budowy. Odległość
między słupem linii elektroenergetycznej i słupem na placu budowy jest równa 15 m,
a wysokości przyłączeń przewodu elektrycznego na słupach są równe odpowiednio 16 m
i 10 m. W sklepie oferowano w promocyjnej cenie zwoje przewodów o długościach:
15 m, 16 m, 17 m i 18 m. Pan Jan wykorzystał okazję i kupił jeden ze zwojów. Długość
kupionego przewodu przewyższała odległość między miejscami przyłączenia na słupach
o mniej niż metr. Oblicz długość przewodu kupionego przez pana Jana. Napisz
obliczenia.
Informacja do zadań 32. i 33.
W pokoju Agnieszki stoi pojemnik z wodą źródlaną. Tuż przy dnie pojemnik ma
zamontowany kurek. Agnieszka zauważyła, że czas potrzebny na napełnienie szklanki
o pojemności 250 ml zależy od wysokości poziomu wody w pojemniku. Dokonała
odpowiednich pomiarów i wyniki zapisała w tabelce:
wysokość poziomu
35 30 25 20 15 10 5
wody (cm)
czas (s)
4,1 4,5 5
5,5 6,2 8,5 11
Zadanie 32. (0-2)
Czy czas potrzebny do napełnienia szklanki jest odwrotnie
proporcjonalny do wysokości
poziomu wody w pojemniku? Odpowiedź uzasadnij.
Odpowiedź:
Zadanie 33. (0-3)
Agnieszka postanowiła wykonać odpowiedni wykres. Narysowała osie układu
współrzędnych i zaczęła zaznaczać punkty odpowiadające danym z tabeli.
Opisz osie i zaznacz brakujące punkty. Oszacuj, na podstawie wykresu, ile czasu
potrzeba do napełnienia szklanki, gdy wysokość poziomu wody jest równa 45 cm.
Odpowiedź: Czas potrzebny.
Zadanie 34. (0-4)
Serek ma kształt graniastosłupa, którego podstawą jest trójkąt o długościach boków:
8 cm, 8 cm i 3 cm. Wojtek i Ewa postanowili podzielić serek na dwie części o równych
objętościach. Wojtek lubi skórkę pokrywającą całą powierzchnię serka, więc
zaproponował cięcie jak na rysunku. Czy rzeczywiście obie części mają tę samą
objętość? Która część ma większą powierzchnię ze skórką? Odpowiedzi uzasadnij.
część I
część II