porównanie dwóch wartości średnich dla populacji o

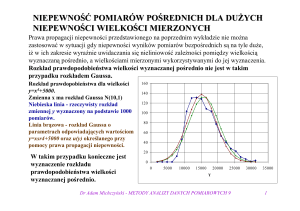
Zadanie 1 (porównanie dwóch wartości średnich dla populacji o rozkładzie normalnym)
Oceniano szybkość wzrostu pewnego gatunku roślin w dwóch różnych temperaturach (w
temp. 20°C i 30°C). W tym celu wysiano po 15 roślin w warunkach kontrolowanych i po 30
dniach oceniono ich wagę. Uzyskano następujące wyniki:
waga w gramach
rośliny w 20°C
rośliny w 30°C
25,6
26,7
28,3
35,6
29,3
31,3
22,8
28,7
27,6
36,1
23,6
29,3
29,6
25,8
32,5
33,6
33,6
38,9
37,8
35,6
32,5
39,8
33,5
40,2
34,5
36,9
28,9
37,6
30,1
33,6
Czy na podstawie uzyskanych wyników możemy powiedzieć, że występuje istotne
zróżnicowanie między średnią szybkością wzrostu w tych dwóch różnych temperaturach?
Zadanie 2
(porównanie dwóch wartości średnich dla populacji o rozkładzie normalnym – próby
zależne - sparowane)
Przeprowadzono ocenę skuteczności pewnego środka odchudzającego. W tym celu na losowo
wybranej grupie osób przetestowano jego skuteczność podając ten środek przez 3 tygodnie.
Poniższa tabela przedstawia wagę osób przed i po 3-tygodniowej kuracji:
nr osoby
waga przed (kg)
waga po (kg)
1
75,3
74,2
2
79,8
79,9
3
55,6
56,3
4
123,5
121,5
5
102,3
103,2
6
96,8
94,5
7
85,6
83,6
8
86,9
85,9
9
75,6
75,6
10
68,3
68,2
11
92,6
92,2
Czy na podstawie uzyskanych wyników możemy powiedzieć, że środek jest skuteczny, czy
tez nie?
Zadanie 3
(porównanie dwóch parametrów p – frakcji w rozkładzie dwupunktowym – zerojedynkowym)
Przeprowadzono ankietę wśród mieszkańców pewnego regionu, w której pytano m.in. o to
czy codziennie spożywają owoce lub warzywa. Spośród wszystkich 1200 osób
ankietowanych było 620 kobiet i 580 mężczyzn. Z tej grupy twierdząco odpowiedziało 425
kobiet i 342 mężczyzn. Czy na podstawie uzyskanych wyników ankiety możemy powiedzieć,
że udział osób spożywających codziennie owoce lub warzywa jest różny wśród kobiet i
mężczyzn w tym regionie?