Ćwiczenie 6

Ćwiczenie 4
Synteza i analiza stanu polaryzacji światła metodą ogólnego prawa Malusa
Pojęcia podstawowe:
Światło spolaryzowane; parametry, określające stan polaryzacji światła; wektor Stokesa; sfera
Poincare;
1. Wstęp
Jednym z zagadnień optyki polaryzacyjnej jest analiza stanu polaryzacji światła,
wychodzącego (bądź odbitego) z nieznanej próbki dwójłomnej. Pozwala to na przykład na
określenie zmian w stanie polaryzacji światła, które wprowadziło badane ciało dwójłomne, a
przez to analizę jego własności. Przy powszechnym dążeniu do automatyzacji pomiarów
tradycyjna metoda analizy stanu polaryzacji światła, oparta na szukaniu minimów jego
natężenia, wydaje się mało obiecująca. Alternatywnym rozwiązaniem może być metoda,
opisana w pracy [1], oparta na pomiarze natężeń badanego światła, przepuszczanego (po
przejściu przez badany obiekt) przez różne analizatory. Bazuje ona na ogólnym prawie
Malusa. Etienne Louis Malus ogłosił w 1808 roku swoje prawo, które mówi, że natężenie I
liniowo spolaryzowanego światła o początkowym natężeniu I0 i kącie azymutu  0  0 , po
przejściu przez doskonały analizator liniowy, umieszczony pod kątem azymutu  , wynosi:
I  I 0 cos 2  .
(1)
W ogólnym przypadku jednak światło padające może być dowolnie i tylko częściowo
spolaryzowane. Również analizator, na który światło to pada, może być eliptyczny i
niedoskonały (to znaczy, współczynniki transmisji fal własnych analizatora nie są równe 0 i
100%). W takim przypadku prawdziwe jest tzw. uogólnione prawo Malusa, podane przez
Ścierskiego [2]:

I  0,5  I 0 t   p0 t  cos c

(2)
gdzie: p 0 jest stopniem polaryzacji światła padającego na analizator, t   t1  t 2 , t   t1  t 2 ,
a t1 i t 2 oznaczają odpowiednio energetyczne współczynniki transmisji fali fal własnych
(pierwszej i drugiej) analizatora. Parametr c jest odległością kątową na sferze Poincare (rys.1)
1
punktu określającego wektor Stokesa stanu polaryzacji światła padającego i pierwszego
wektora własnego analizatora. Można go obliczyć z iloczynu skalarnego odpowiednich
wektorów Stokesa:
cos c  M 1 M 0  C1C0  S1 S 0
(3)
gdzie V1   M 1 , C1 , S1  jest wektorem Stokesa pierwszego wektora własnego analizatora a
V0   M 0 , C0 , S 0 
jest jednostkowym (tzn. unormowanym) wektorem Stokesa nieznanego
światła padającego. Konstrukcja na sferze Poincare, jakkolwiek dość trudna w odbiorze przez
adeptów tajemnych nauk optyki polaryzacyjnej, znakomicie wyjaśnia ideę metody, na której
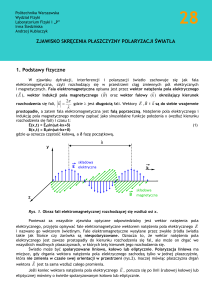
oparty jest układ pomiarowy niniejszego ćwiczenia. Jak widać na Rys.1, po zmierzeniu
natężenia światła wychodzącego z analizatora (przy założeniu, że znamy jego parametry
M1 , C1 , S1 
oraz t1 i t 2 ), możemy stwierdzić, że możliwe są tylko takie stany polaryzacji
światła padającego, których jednostkowe wektory Stokesa reprezentowane są przez punkty,
leżące na sferze Poincare na kole o środku [V1] promieniu c1.
Rys.1 Możliwe stany polaryzacji światła badanego leżą na kole o środku [V 1] i promieniu c1 (objaśnienia
wielkości – patrz tekst).
Oczywiście, nie pozwala to na jednoznaczne określenie żądanego stanu polaryzacji, ale
pokazuje nam dalszą drogę postępowania. Należy mianowicie zmienić analizator – i na sferze
powstanie nowe koło, zakreślone z nowego punktu [V2] promieniem c2. Ponieważ światło
badane jest to samo, jego stan polaryzacji określa punkt na przecięciu obu wspomnianych kół!
Ze względu na to jednak, że – pomijając szczególne przypadki – dwa koła przecinają się w
dwóch punktach, niezbędne będzie przeprowadzenie trzeciego pomiaru ([V2], c3), który
jednoznacznie rozstrzygnie, z jakim stanem polaryzacji światła na wejściu układu mamy do
czynienia. Obrazuje to rys.2.
2
Rys.2 Możliwe stany polaryzacji światła badanego leżą na przecięciu trzech kół o środkach [V 1], [V1] i [V1] i
promieniach c1, c2 i c3 (objaśnienia wielkości – patrz tekst).
Nasze rozważania, bazujące na graficznej reprezentacji stanu polaryzacji światła na
sferze Poincare, „podeprzemy” odpowiednimi równaniami, korzystając z formalizmu
Stokesa. Napiszmy równanie (2) dla trzech różnych analizatorów i tego samego wejściowego
stanu polaryzacji światła, czyli zastosujmy trzykrotnie uogólnione prawo Malusa:

I i  0,5  I 0 t i  p0 t i cos ci

(4)
gdzie:
cos ci  M i M 0  Ci C0  S i S 0
(5)
a i=1,2,3. Wprowadźmy też parametry Ai , zależne od wielkości mierzonych bezpośrednio, to
znaczy względnego natężenia światła oraz od stałych materiałowych analizatorów:
2
Ai 
Ii
 t i
I0
t i
(6)
(zauważmy, że parametry t  i t  mają teraz indeksy „i”, oznaczające wartości tychże
parametrów dla trzech różnych analizatorów na wyjściu!). Wtedy równania (4) (tak,
pamiętajmy, że to są trzy równania!) można zapisać następująco:
 A1   M 1
 A   M
 2  2
 A3   M 3
C1
C2
C3
S1   p 0 M 0 
S 2    p0 C0  .
S 3   p0 S 0 
(7)
Po lewej stronie równania (7) mamy wektor, stworzony z (uzyskanych z pomiarów natężeń)
parametrów Ai . Po prawej – macierz parametrów analizatorów i interesujący nas wektor,
3
opisujący stan polaryzacji światła badanego. Analiza warunków rozwiązalności równania (7)
doprowadza nas do wniosku, że możliwy jest dowolny wybór trzech analizatorów z
zachowaniem warunku nie zerowania się wyznacznika macierzy z prawej strony tego
równania. Analiza rysunku na sferze Poincare pozwala ten warunek wyrazić bardziej
„strawnie” dla optyka – ograniczeniem wyboru naszych analizatorów jest warunek, aby
punkty, reprezentujące ich wektory własne, nie leżały na wielkim kole sfery Poincare (stąd
wniosek, że – niestety! – nie można w szczególności użyć trzech analizatorów liniowych bo
reprezentujące je punkty leżą na równiku sfery Poincare).
Rozwiązanie równania (7), w którym niewiadome znajdują się po jego prawej stronie i
są mnożone przez pewną macierz, nie jest ogólnie proste i wymaga wyznaczenia macierzy
odwrotnej do macierzy parametrów analizatorów (stąd powyższy warunek na wyznacznik tej
macierzy). Nie będziemy się spierać, czy idea ułatwienia operacji rozwiązywania równania
(7) wynika z baczniejszego przyjrzenia się rysunkowi na sferze Poincare czy rozważań
analitycznych, ale stwierdzimy, że rozwiązanie to będzie szczególnie proste, jeśli przyjmiemy
następujący układ analizatorów:
-
pierwszy liniowy, o kącie azymutu 1  0 , czyli: M 1  1 ; C1  0 i S1  0 ;
-
drugi również liniowy, o kącie azymutu  2  45 , czyli: M 2  0 ; C2  1 i S 2  0 ;
-
trzeci kołowy prawoskrętny, czyli: M 3  0 ; C3  0 i S 3  1 .
Przy takim wyborze analizatorów równanie (7) przybiera szczególnie prostą postać, ponieważ
macierz z prawej strony równania staje się macierzą jednostkową:
 A1  1 0 0  p0 M 0 
 A   0 1 0   p C 
 2 
  0 0
 A3  0 0 1  p0 S 0 
(7a)
i rozwiązanie go można podać niezwłocznie jako:
M0 
A1
p0
C0 
A2
p0
S0 
A3
p0
(8)
gdzie parametr p 0 (stopień polaryzacji światła padającego) otrzymujemy z równania:
p0  A12  A22  A32
(9)
wykorzystującego warunek normowania wektora Stokesa V0   M 0 , C 0 , S 0  wejściowego
stanu polaryzacji. Pozostaje jeszcze wyliczenie parametrów stanu polaryzacji światła
wejściowego, a więc kąta azymutu  i kąta eliptyczności  , które obliczymy ze znanych
zależności:
4
  0,5  arcsin S 0 ,
(10a)
 C0 
 .
 M0 
  0,5  arctan 
(10b)
2. Przebieg pomiarów
Pomiarów dokonujemy w układzie polarymetru, opisanego oddzielnie w instrukcji
roboczej. Przed przystąpieniem do wykonania ćwiczenia należy zapoznać się z instrukcją
roboczą przy stanowisku pomiarowym – zwrócić szczególna uwagę na sposób
justowania układu oraz zalecenia dotyczące ustawień mocy. Pierwsze dwa elementy
polarymetru – polaryzator oraz płytka ćwierćfalowa – będą nam służyły do zsyntetyzowania
badanego stanu polaryzacji światła. Zalecane jest przeprowadzenie kilku pomiarów dla kilku
stanów polaryzacji światła na wejściu układu – podanych przez prowadzącego bądź według
własnego uznania ale z zaleceniem, aby zacząć od prostych stanów liniowych a skończyć na
kołowym. W istniejącym układzie nie ma, jak na razie, możliwości wytworzenia światła
częściowo spolaryzowanego, dlatego obliczenia, dotyczące wyznaczania parametru p 0 będą
miały nieco inny sens – patrz niżej.
A) Wyznaczenie parametrów transmisyjnych układu.
Trzy analizatory (dwa liniowe i jeden kołowy), opisane we „Wstępie”, realizowane są
w układzie pomiarowym poprzez użycie drugiego polaryzatora i (w przypadku analizatora
trzeciego, kołowego) użycie drugiej płytki ćwierćfalowej. Przed przystąpieniem do
właściwych pomiarów niezbędne jest wobec tego wyznaczenie parametrów t  i
t, a
dokładniej: t1 i t 2 - czyli współczynników energetycznych (natężeniowych) poszczególnych
analizatorów. Zakładamy, że oba polaryzatory użyte w układzie (wejściowy i wyjściowy,
pełniący funkcję analizatora) są takie same jak również, że takie same parametry mają obie
ćwierćfalówki. Założenie to jest o tyle usprawiedliwione, że analogiczne elementy układu
pomiarowego zostały wykonane z tych samych materiałów i w ten sam sposób. Dalej,
przyjmiemy za oczywiste założenie, że oba linowe analizatory, a więc ten o kącie azymutu 0
oraz ten o kącie 45, mają te same parametry t1lin i t 2lin - bo przecież jest to fizycznie ten sam
analizator, tylko obrócony o 45 (użyliśmy teraz w oznaczeniach transmisji dodatkowo
indeksów górnych dla podkreślenia, że dalsze rozważania dotyczyć będą odpowiednich
współczynników dla dwóch pierwszych analizatorów liniowych). Aby wyznaczyć
natężeniowy współczynnik t1 transmisji fali pierwszej (czyli tej, która przepuszczana jest w
5
sposób maksymalny) bądź t 2 drugiej (tej, którą analizator maksymalnie tłumi) w danym
analizatorze, musimy wytworzyć stan polaryzacji odpowiadający danej fali i zmierzyć
natężenie wiązki świetlnej przed i po przejściu przez analizator. W przypadku analizatorów
liniowych jest to szczególnie proste, bo wystarczy ustawić pierwszy z nich pod kątem
azymutu 0, zmierzyć natężenie wiązki światła z niego wychodzącej, a następnie wprowadzić
w bieg wiązki drugi polaryzator (pełniący w układzie funkcję analizatora) najpierw pod kątem
azymutu 0 po czym drugi raz – pod kątem azymutu 90. Stosunki poszczególnych natężeń
dadzą nam szukane wartości parametrów t1lin i t 2lin . Zauważmy, że w proponowanym
schemacie zmieniliśmy azymut drugiego polaryzatora (analizatora), a nie pierwszego, jak
sugerowałby opis kilka linijek wyżej, a to dlatego, że ważne jest względne położenie obu
polaryzatorów a obrót pierwszego mógłby zmienić natężenie wiązki odniesienia (ze względu
na użycie światła laserowego na wejściu, które jest przecież spolaryzowane...). Schemat
ideowy pomiaru wartości t1lin i t 2lin obrazuje rys.3.
a)
I
Natężenie
wiązki
odniesienia
Polaryzator
  0
b)
Polaryzator
  0
t1lin 
I1
I
I2
t 2lin 
I2
I
Analizator
  0
c)
Polaryzator
  0
I1
Analizator
  90
Rys.3 Schemat pomiaru natężeniowych współczynników transmisji polaryzatorów liniowych
6
Podobnie zmierzymy natężeniowe współczynniki transmisji t1kol i t 2kol fali pierwszej i
drugiej dla analizatora kołowego. Trzeba teraz zsyntetyzować na wejściu na światło
spolaryzowane kołowo, na przykład prawoskrętnie, i zmierzyć natężenie wiązki odniesienia
oraz po przejściu przez analizatory kołowe o zgodnej i przeciwnej skrętności. Schemat
pomiarów ilustruje Rys.4.
a)
I
Polaryzator Ćwierćfalówka
  0
  45
b)
Polaryzator Ćwierćfalówka
  0
  45
I1
t1kol 
I1
I
I2
t 2kol 
I2
I
Ćwierćfalówka Analizator
  45
  0
c)
Polaryzator Ćwierćfalówka
  0
  45
Ćwierćfalówka Analizator
  45
  0
Rys.4 Schemat pomiaru natężeniowych współczynników transmisji polaryzatora kołowego prawoskrętnego.
Współczynniki transmisji t1lin i t 2lin oraz t1kol i t 2kol należy wyznaczyć szczególnie
starannie, ponieważ wielkości te wchodzą kilkakrotnie w paru kombinacjach (jako
odpowiednie t  i t  ) do wzorów na wielkości Ai (pamiętajmy, że do wzorów na A1 i A2
podstawiamy t  i t  obliczone z t1lin i t 2lin , a do wzoru na A3 wstawiamy t  i t  wyliczone
z t1kol i t 2kol ). Dlatego zalecane jest wielokrotne powtórzenie pomiarów poszczególnych
natężeń światła przed i po przejściu przez używane analizatory (liniowy i kołowy) i obliczenie
odpowiednich średnich.
7
B) Synteza wybranych stanów polaryzacji światła i ich analiza metodą uogólnionego
prawa Malusa.
Należy wyznaczyć parametry polaryzacyjne (czyli: kąt azymutu  , kąt eliptyczności

oraz (formalnie) stopień polaryzacji
p0
kilku wybranych stanów polaryzacji,
zsyntetyzowanych uprzednio przez ćwiczących. Synteza stanu polaryzacji światła
realizowana jest przy użyciu liniowego polaryzatora i liniowej płytki ćwierćfalowej według
schematu, opisanego na przykład w podręczniku [3] (rozdział 12). Przypomnijmy tylko, że:
aby otrzymać światło spolaryzowane eliptycznie z kątem eliptyczności  i kątem
azymutu  , należy przepuścić światło najpierw przez liniowy polaryzator ustawiony
pod kątem azymutu  p     a następnie przez liniową ćwierćfalówkę, której
pierwszy wektor własny ma azymut  cw   .
Następnie przystępujemy do właściwych pomiarów, czyli zmierzymy kolejno cztery
natężenia światła:
-
„odniesienia” ( I 0 ), a więc wychodzące z układu syntetyzującego;
-
po przejściu przez pierwszy analizator - liniowy o kącie azymutu   0 ( I 1 );
-
po przejściu przez drugi analizator - liniowy o kącie azymutu   45 ( I 2 );
-
po przejściu przez trzeci analizator - kołowy prawoskrętny   45 ( I 3 ).
3. Opracowanie wyników
Wstawiając zmierzone wartości natężeń oraz uprzednio zmierzone współczynniki
transmisji analizatorów do wzorów (6) otrzymujemy szukane współczynniki Ai . Teraz
pozostaje już tylko wyliczenie parametrów badanego stanu polaryzacji światła. Pierwszym
obliczeniem powinno być wyliczenie stopnia polaryzacji. W naszym ćwiczeniu używamy „z
definicji” (laser!) światła spolaryzowanego całkowicie, więc wyliczenie pierwszego
parametru – stopnia polaryzacji p 0 – ma raczej sens unormowania wyników pomiarowych.
Wiadomo, że wszelkie pomiary są obarczone błędami, więc proponujemy raczej wyliczenie
parametru p 0 ze wzoru (9) a następnie wyliczenie unormowanych parametrów M 0 , C0 , S 0 
pierwszego wektora Stokesa badanego światła ze wzorów (8). Ostatnim krokiem będzie
obliczenie parametrów  i  ze wzorów (10). Należy oczywiście zadbać o należytą formę
prezentacji wyników, to znaczy aby kąt azymutu  zawierał się w przedziale (0, 180) a kąt
8
eliptyczności  w przedziale (-45, 45). Otrzymane wyniki porównujemy z parametrami
polaryzacyjnymi (  ,  ) światła, które wcześniej zsyntetyzowaliśmy.
Literatura
[1] F. Ratajczyk, W.A. Woźniak, P. Kurzynowski, „The method of measurement of light
polarization state using the general Malus law”, Optik 99, 180 (1995)
[2 ] I. Ścierski, „General Malus law”, Optik 71, 61 (1985)
[3] F. Ratajczyk, „Dwójłomność i polaryzacja optyczna”, Oficyna Wydawnicza Politechniki
Wrocławskiej, Wrocław 2000
9