W-21 (Jaroszewicz) 16 slajdów
Na podstawie prezentacji prof. J. Rutkowskiego
Optyka falowa
polaryzacja
czym jest zjawisko polaryzacji
stan a stopień polaryzacji
sposoby polaryzacji
dwójłomność optyczna
przyczyny mikroskopowe
zastosowania
Polaryzacja
światła
z
E
B
x
Fala EM jest spolaryzowana gdy wektory E i B mają
ustalony kierunek w przestrzeni
y
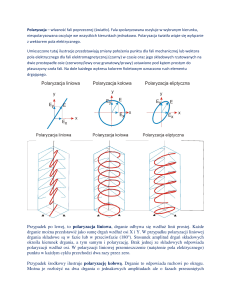
polaryzacja liniowa – wektor E drga w jednym kierunku
polaryzacja kołowa – wektor E zatacza koła
Polaryzacja jest zjawiskiem, które występuje tylko
dla fal poprzecznych
Kierunek polaryzacji to kierunek drgań wektora E
Światło wysyłane przez wiele źródeł – atomów jest
niespolaryzowane – składa się z wielu różnych
kierunków polaryzacji
E
światło niespolaryzowane jest superpozycją
dwóch fal spolaryzowanych wzajemnie prostopadle
D. Goldstein: Polarized Light, Marcel Dekker Inc., New York, 2003
Polaryzacją nazywamy wektorową naturę światła
→ →
→
r , t exp i ϕ r , t
→ →
Ψ r , t = A
→ →
sens
fizyczny
→ →
Re[ Ψ r , t ]
=>
→ →
→ →
→ →
Ψ r , t = E r , t lub H r , t
Dla fali plaskiej
→ →
→ → →
→ →
w kierunku ' z '
E r , t ≡ A r , t e cos(ωt + k ⋅ r ) → E r , t ≡ Et cos(ωt − kz )
Stan polaryzacji
- SOP
Azymut θ – kąt pomiędzy
dużą osią elipsy, a
kierunkiem osi 0x,
Kąt eliptyczności ε – którego tangens jest
stosunkiem długości małej do dużej półosi elipsy
polaryzacji ε=tg(b/a)
Amplituda drgania elektrycznego R- która charakteryzuje
‘wielkość’ drgania elektrycznego, jej kwadrat jest proporcjonalny
do gęstości energii w danym punkcie pola: R=(a2+b2)1/2
Stopień polaryzacji - DOP [M. Born, E. Wolf, Principle
of Optics, Pergamon NY, 1968]
I
I0
IP
IP
P=
I0
natężenie części spolaryzowanej
wiązki świetlnej
całkowite natężenie wiązki
świetlnej
kąt polaryzatora
Światło:
- Całkowicie spolaryzowane P=1,
- Częściowo spolaryzowane P<1,
- Zdepolaryzowane P=0
SPOSOBY POLARYZACJI
fala
spolaryzowana
równolegle
ODBICIE
α
900
β
fala
spolaryzowana
w płaszczyźnie
padania
Dwie składowe wektora E padającej fali:
•prostopadła do płaszczyzny padania ,
•leżąca w płaszczyźnie padania.
Jeśli α+β=90, to fala
całkowicie spolaryzowana.
Kąt Brewstera
Jeśli α+β=90, to n=sinα/sinβ=sinα/sin(90-α)
POLARYZATORY
Fala padająca Epad
E
polaryzator: metalowe
pręty (mikrofale, fale
radiowe) długie
cząsteczki (światło)
Fala
przepuszczona
odbita
jest
n = tgα
oś polaryzatora – linia
prostopadła do prętów
E=Epad+Epręty=0
Fala
wytworzona
przez prąd
Epręty= -E
Fala
przepuszczona
=fala padająca
Wygaszenie lub
przepuszczenie fali jest
wynikiem interferencji fali
padającej i wytworzonej
w materiale polaryzatora
PRAWO MALUSA
Fala padająca
Epad pod
kątem do osi
polaryzatora
Ezatrzym
Epad
I = Imcos2θ
θ
Przepuszczona
tylko składowa
równoległa do osi
polaryzatora
polaryzator
analizator
Eprzep
Eprzep=Epad cosθ
Prawo Malusa – natężenie światła
spolaryzowanego po przejściu przez
analizator optyczny jest
proporcjonalne do kwadratu cosinusa
kąta pomiędzy płaszczyznami
polaryzacji światła przed i po przejściu
przez analizator
(reguła kwadratu cosinusa)
SKRĘCENIE PŁASZCZYZNY POLARYZACJI
polaryzator
fala zupełnie wygaszona
Zwiększenie ilości płytek polaryzacyjnych nie
zmienia kąta skręcenia, lecz zwiększa
natężenie przepuszczonej (i skręconej) fali
1.00
0.98
Eprzep=Epad cosn (θ/n)
0.96
0.94
0.92
0
5
10
15
20
część fali przechodzi
Możliwe jest skręcenie
płaszczyzny polaryzacji fali
WYŚWIETLACZE CIEKŁOKRYSTALICZNE
Ciekłe kryształy to stan pośredni miedzy cieczą, a kryształem
• cząsteczki mogą znajdować się w zupełnie przypadkowych położeniach (jak w cieczy)
• są zorientowane jedne względem drugich (uporządkowanie jak w kryształach). )
Takie własności wynikają z wydłużonego kształtu molekuł przy jednocześnie małej T,
dzięki czemu lokalny porządek nie jest niszczony przez fluktuacje termiczne
Częściowo roztopione mydło
jest ciekłym kryształem
Ciekłe kryształy mają
unikalne własności
fizyczne.
y
E
z
x
E
x
Po przejściu przez ciekły kryształ płaszczyzna polaryzacji fali
jest skręcona, lecz fala nie jest osłabiona
Dwójłomność
Jest to własność ośrodków optycznych do podwójnego załamywania
światła (rozdwojenia promienia świetlnego). Substancje dla których zjawisko zachodzi nazywamy substancjami dwójłomnymi.
Zjawisko dwójłomności odkrył w 1669 roku Rasmus Bartholin, zaś wyjaśnił
Augustin J. Fresnel w pierwszej połowie XIX w wieku.
Dwójłomność wykazuje wiele substancji krystalicznych, a także wszystkie
ciekłe kryształy. Przykładami substancji dwójłomnych mogą być kryształy rytylu i kalcytu.
Terminem tym określa się także różnice między współczynnikiem załamania promienia nadzwyczajnego ne, a współczynnikiem załamania promienia zwyczajnego no.
∆n= ne - no
Dwójłomność - wyjaśnienie
Zjawisko wynika z faktu, że substancja jest anizotropowa, co
oznacza że współczynniki przenikalności elektrycznej ε i wynikająca
z niego prędkość światła, stąd współczynnik załamania światła, w
krysztale zależą od kierunku drgań pola elektrycznego fali elektromagnetycznej (polaryzacji fali).
W krysztale takim istnieje oś optyczna - kierunek w którym światło
biegnąc nie rozdziela się na dwa promienie, ponieważ prędkość
światła jest taka sama dla wszystkich możliwych polaryzacji fali
biegnącej w tym kierunku. Kierunek tej osi nie zależy od kształtu
kryształu. Istnieją kryształy jedno i dwuosiowe.
Promień zwyczajny
i nadzwyczajny
fala
spolaryzowana
równolegle
ODBICIE
α
900
β
fala spolaryzowana
w płaszczyźnie
padania
W krysztale jednoosiowym podczas załamania promień wchodzący do
kryształu rozdziela się na dwa, jeden z nich jest to promień zwyczajny,
spełnia on prawo Snelliusa, leży on w płaszczyźnie padania, oznaczany jest
symbolem o (ang. ordinary). Dla tego promienia kierunek drgań pola
elektrycznego jest prostopadły do jego płaszczyzny głównej.
Drugi promień to promień nadzwyczajny, nazywa się go tak, bo w ogólności nie spełnia on prawa Snelliusa, oznacza się go przez e (ang.
extraordinary). Promień ten nie musi leżeć w płaszczyźnie padania, może się
także załamać, gdy promień pada prostopadle do powierzchni kryształu. To
w jaki sposób zmieni on kierunek przy takim padaniu, zależy od kierunku osi
optycznej w krysztale. Nie załamie się kiedy oś optyczna jest prostopadła lub
równoległa do powierzchni na którą pada promień. Dla promienia nadzwyczajnego kierunek drgań pola elektrycznego jest równoległy do jego płaszczyzny głównej. Warto zauważyć, że ponieważ płaszczyzny główne obu
promieni mogą być inne, polaryzacje obu promieni nie muszą być do siebie
prostopadłe.
W krysztale dwuosiowym oba promienie zachowują się jak promienie
nadzwyczajne.
Dwójłomność – przyczyny
mikroskopowe
Istnienie dwójłomności osi optycznej w krysztale wynika z jednakowego
kierunku ustawienia jego anizotropowych cząsteczek. Cząsteczki takiego
kryształu mają zazwyczaj wydłużony kształt i ułożone są w krysztale
regularnie. W takim ujęciu oś optyczna jest to kierunek osi symetrii tych
cząstek.
Zjawisko dwójłomności może się także pojawić pod wpływem czynników
zewnętrznych, jak pole elektryczne (elektrooptyczne zjawisko Kerra), pole
magnetyczne (zjawisko Faradaya), fala elektromagnetyczna (optyczne
zjawisko Kerra). Wynika to z faktu, że anizotropowe cząsteczki nie są
ułożone regularnie, ale mogą posiadać ładunki na swoich końcach (są
dipolami), wtedy pod wpływem pola elektrycznego układają się odpowiednio
do niego, zjawisko wykorzystywane jest w ekranach LCD. Nieuszeregowane
cząsteczki mogą być także uporządkowane pod wpływem ściskania lub
rozciągania materiału (tak jak prostują się pozwijane nitki kiedy są
rozciągane).
WYŚWIETLACZE CIEKŁOKRYSTALICZNE
Nie spolaryzowane światło
Polaryzator
Płytka szklana z
nacięciami
Oś ciekłych kryształów wzdłuż
nacięć
Ciekłe kryształy
Starają się ustawić równolegle
do siebie
Płytka szklana z
nacięciami
Oś ciekłych kryształów wzdłuż
nacięć
Analizator
Kierunek osi ciekłego kryształu może być zmieniany przez zewnętrzne pole elektryczne
WYŚWIETLACZE CIEKŁOKRYSTALICZNE
Nie spolaryzowane światło
Włączenie napięcia powoduje, że
osie ciekłych kryształów ustawiają
się równolegle do pola elektrycznego
ciekłe kryształy nie skręcają
płaszczyzny polaryzacji
Brak napięcia
światło przechodzi
Przyłożenie napięcia
światło nie
przechodzi