Algorytm Euklidesa – NWD

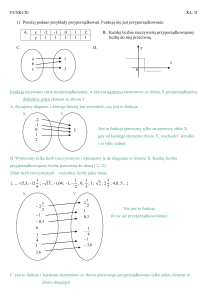
Algorytm znajdowania
Największego Wspólnego
Dzielnika
Definicja NWD i przykłady
Największym wspólnym dzielnikiem (NWD)
dwóch lub więcej liczb naturalnych dodatnich
nazywamy największą liczbę naturalną,
która jest jednocześnie dzielnikiem każdej z liczb.
NWD(2,8)=2
NWD(5,6)=1
NWD(6,15)=3
NWD(42,56)=14
NWD(140,60,50)=10
Prosty sposób znajdowania NWD
Szukając NWD liczb rozkładamy je na czynniki pierwsze,
a następnie wyznaczamy iloczyn czynników
występujących w obu rozkładach.
Szukamy NWD(42,56)
42|2
56|2
21|3
28|2
7|7
14|2
1|
7|7
1|
NWD(42,56)=2*7=14
Algorytm Euklidesa
• Ustalamy dwie liczby naturalne a i b, t. że a>b.
• Obliczamy różnicę a-b.
• Porównujemy b z a-b.
•
Jeżeli są równe znaleźliśmy NWD.
Jeśli nie to znów od większej odejmujemy
mniejszą.
Procedurę tę powtarzamy aż do uzyskania
równości.
Schemat blokowy Algorytmu Euklidesa
Zastosowanie Algorytmu Euklidesa
Szukamy NWD(112; 44)
112; 44
68; 44
112 – 44 = 68
68-44=24
44; 24
24; 20
20; 4
44-24=20
24-20=4
20-4=16
16; 4
12; 4
8; 4
4; 4
16-4=12
12-4=8
8-4=4
STOP
NWD(112; 44) = 4