FUNKCJE
KL. II
1) Poniżej podano przykłady przyporządkowań. Funkcją nie jest przyporządkowanie:
A.
x
y
-2
1
-1
1
0
1
1
1
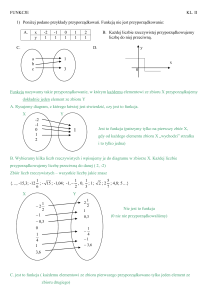
B. Każdej liczbie rzeczywistej przyporządkowujemy
liczbę do niej przeciwną.
2
1
C.
D.
a
b
c
y
1
x
3
0
Funkcją nazywamy takie przyporządkowanie, w którym każdemu elementowi ze zbioru X przyporządkujemy
dokładnie jeden element ze zbioru Y
A. Rysujemy diagram, z którego łatwiej jest stwierdzić, czy jest to funkcja.
X
Y
-2
-1
0
1
2
Jest to funkcja (patrzymy tylko na pierwszy zbiór X,
1
gdy od każdego elementu zbioru X „wychodzi” strzałka
i to tylko jedna)
B. Wybieramy kilka liczb rzeczywistych i wpisujemy je do diagramu w zbiorze X. Każdej liczbie
przyporządkowujemy liczbę przeciwną do danej ( 2, -2)
Zbiór liczb rzeczywistych – wszystkie liczby jakie znasz
1
1
1
{…, -15,3; -12 ; - 15 ; -1,04; -1, , 0, ; 1;
6
3
2
X
5
2 ; 2 ; 4,8; 5…}
7
Y
1
2
2
1
0,3
0
2
1
2
1
0,3
Nie jest to funkcja
(0 nic nie przyporządkowaliśmy)
1
4
1
1
4
1
3,6
3,6
C. jest to funkcja ( każdemu elementowi ze zbioru pierwszego przyporządkowano tylko jeden element ze
zbioru drugiego)
D.
y
Nie jest to funkcja (każda prosta równoległa do osi y może
x
mieć z wykresem funkcji najwyżej jeden punkt wspólny)
2) Określ dziedzinę funkcji:
a) f(x) = 2 5 x
b) g ( x)
5
x 1
Dziedzina funkcji to zbiór wszystkich liczb rzeczywistych, dla których można obliczyć wartość funkcji.
Pod pierwiastkiem kwadratowym wyrażenie 2 – 5x musi być większe lub równe 0
a)
2 – 5x 0 / - 2
przenosimy liczbę 2 ze zmienionym znakiem na prawą stronę nierówności czyli – 2
2- 5x -2 0 – 2
- 5x – 2 / : (-5) dzielę przez liczbę – 5 czyli przez liczbę przy x. Zawsze zmieniam znak nierówności na
przeciwny, gdy dzielę przez liczbę ujemną.
x
2
5
2
5
0
1
2
D f = ( - , >
5
Gdy występuje ułamek, wyrażenie w mianowniku x – 1 nie może przyjmować wartości 0 czyli x – 1
b)
musi być różne od 0
x – 1 0 / +1
przenoszę liczbę – 1 na prawą stronę ze zmienionym znakiem czyli + 1
x–1+1 0+1
x 1
D f = R – {1}
3) Sporządź tabelkę funkcji f (x ) x 1 dla argumentów 2, 1, 0, 1, 2 i wyznacz jej zbiór wartości.
2
Obliczamy wartości funkcji podstawiając w miejsce x kolejne liczby argumentów -2, -1, 0, 1, 2.
f(- 2) = (-2 -1) 2 = (- 3) 2 = 9
f(- 1) = (-1 -1) 2 = (- 2) 2 = 4
f(0) = (0 -1) 2 = (- 1) 2 = 1
f(1) = (1 -1) 2 = 0 2 = 0
f(2) = (2 -1) 2 = 1 2 = 1
x
f(x) = (x-1) 2
-2
9
-1
4
0
1
1
0
2
1
Dziedzina
Zbiór wartości
ZW f = {0, 1, 4, 9}
4) Narysuj wykres funkcji f(x) = x dla:
xC
a)
x (-1, 3>
b)
a) C = {… -3, -2, -1, 0, 1, 2, 3,…}
Obliczamy wartości funkcji podstawiając w miejsce x kolejne liczby argumentów
-3, -2, -1, 0, 1, 2, 3.
x
-3
3
f(x) = x
-2
2
-1
1
0
0
1
1
2
2
3
3
f(- 3) = 3 = 3
Wartość bezwzględna liczby ujemnej i dodatniej jest liczbą
f(- 2) = 2 = 2
dodatnią.
f(- 1) = 1 = 1
Wartość bezwzględna zera równa się zero.
f(0) = 0 = 0
f(1) = 1 = 1
f(2) = 2 = 2
f( 3) = 3 = 3
y
3
2
1
0
-4
-3
-2
-1
0
1
2
3
4
b) x (-1, 3>
x
f(x) = x
-1
1
f(- 1) = 1 = 1
0
0
1
1
2
2
3
3
y
f(0) = 0 = 0
f(1) = 1 = 1
f(2) = 2 = 2
f( 3) = 3 = 3
1
1
x
5) Funkcja f przyporządkowuje każdej liczbie naturalnej n należącej do zbioru {3, 4, 5, 6, 7, 8} największy
wspólny dzielnik liczb n i 10.
a) Sporządź tabelkę wartości tej funkcji f
b) Podaj zbiór wartości funkcji f.
Szukamy największych wspólnych dzielników liczb 3 i 10, 4 i 10, 5 i 10, 6 i 10, 7 i 10, 8 i 10.
Dzielnikami liczby 3 są 1 i 3. Zapisujemy krócej D 3 = {1, 3}
Dzielnikami liczby 10 są 1, 2, 5, 10. Zapisujemy krócej D 10 = {1, 2, 5, 10}
Największy wspólny dzielnik czyli NWD (3, 10) = 1
NWD (3, 10) = 1
NWD (4, 10) = 2
D 4 = {1, 2, 4}
D 10 = {1, 2, 5, 10}
NWD (5, 10) = 5
D 5 = {1, 5}
D 10 = {1, 2, 5, 10}
NWD (6, 10) = 2
D 6 = {1, 2, 3, 6}
D 10 = {1, 2, 5, 10}
NWD (7, 10) = 1
D 7 = {1, 7}
D 10 = {1, 2, 5, 10}
NWD (8, 10) = 2
D 8 = {1, 2, 4, 8}
D 10 = {1, 2, 5, 10}
x
-2
-1
0
1
2
y
1
1
1
1
1
ZW f = {1, 2, 5}
6) Na rysunku przedstawiono wykres funkcji f. Korzystając z wykresu, odpowiedz:
a) Jaka jest dziedzina funkcji f ?
b) Jaki jest zbiór wartości funkcji f ?
c) Jakie są miejsca zerowe funkcji f ?
d) Dla jakich argumentów funkcja f przyjmuje wartości dodatnie ?
e) Podaj najmniejszą i największą wartość funkcji (o ile istnieje).
y
1
1
x
a)
D f = <-6, 6)
Dziedzinę funkcji odczytujemy na osi x
b)
c)
Zw f = <- 3, 3>
f(x) = 0 dla x = -5, x = -1, x = 5
Zbiór wartości odczytujemy na osi y
Miejsce zerowe funkcji to argument czyli x, w którym
wykres przecina oś x
d)
wartość najmniejsza y = - 3 dla x = -6
wartość największa – nie istnieje