DYFRAKCJA NA POJEDYNCZEJ I PODWÓJNEJ SZCZELINIE IV

Ćwiczenie O-19
DYFRAKCJA NA POJEDYNCZEJ I PODWÓJNEJ SZCZELINIE
I.
Cel ćwiczenia: zapoznanie ze zjawiskiem dyfrakcji światła na pojedynczej i podwójnej
szczelinie. Pomiar długości fali światła laserowego i szerokości pojedynczej szczeliny.
II.
Przyrządy:
III. Literatura
laser LG 200 (λ = 632,8 nm), zestaw szczelin pojedynczych i podwójnych,
ekran, miarka milimetrowa.
1. D. Resnick, R. Holliday Fizyka, t.II.
2. F. C. Crawford Fale,
IV. Wstęp
Dyfrakcja jest to zjawisko polegające na uginaniu się promieni świetlnych przechodzących w
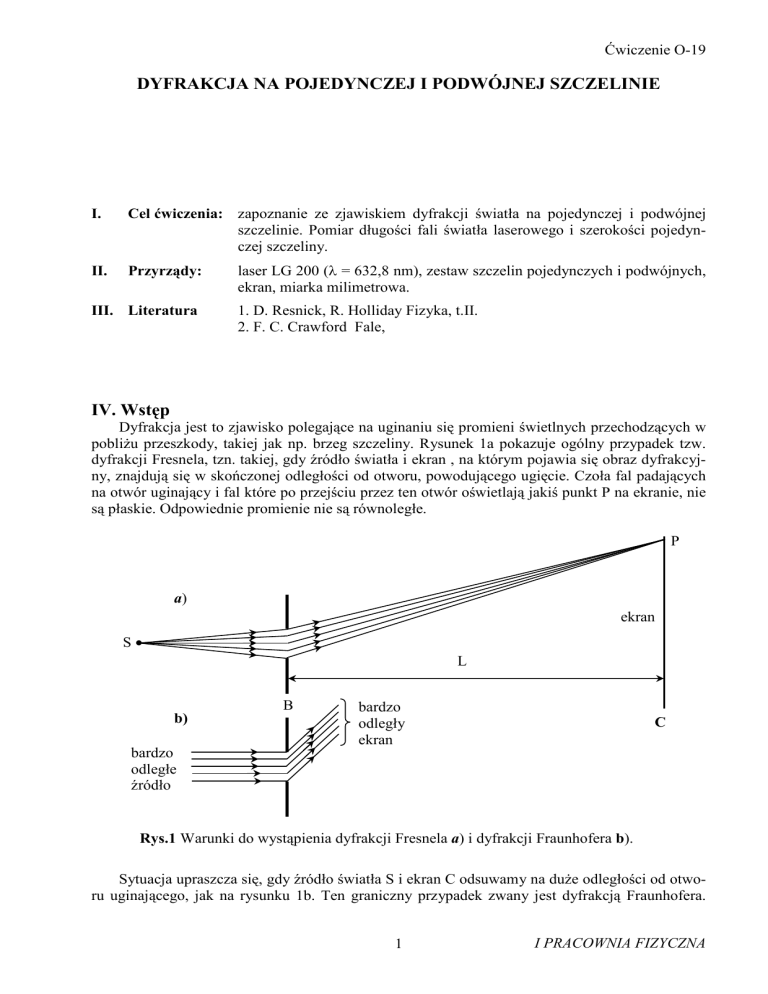
pobliżu przeszkody, takiej jak np. brzeg szczeliny. Rysunek 1a pokazuje ogólny przypadek tzw.
dyfrakcji Fresnela, tzn. takiej, gdy źródło światła i ekran , na którym pojawia się obraz dyfrakcyjny, znajdują się w skończonej odległości od otworu, powodującego ugięcie. Czoła fal padających
na otwór uginający i fal które po przejściu przez ten otwór oświetlają jakiś punkt P na ekranie, nie
są płaskie. Odpowiednie promienie nie są równoległe.
P
a)
ekran
S•
L
B
b)
bardzo
odległy
ekran
C
bardzo
odległe
źródło
Rys.1 Warunki do wystąpienia dyfrakcji Fresnela a) i dyfrakcji Fraunhofera b).
Sytuacja upraszcza się, gdy źródło światła S i ekran C odsuwamy na duże odległości od otworu uginającego, jak na rysunku 1b. Ten graniczny przypadek zwany jest dyfrakcją Fraunhofera.
1
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Czoła fal padających na otwór uginający z odległego źródła są płaszczyznami a odpowiadające im
promienie są do siebie równoległe. Podobnie czoła fal padających na jakiś punkt P na odległym
ekranie C są płaskie.
Nałożenie się na siebie dwóch fal o tej samej częstości i stałej różnicy fazy (czyli spójnych)
poruszających się w przybliżeniu w tym samym kierunku, powoduje, że ich energia nie jest rozłożona w przestrzeni równomiernie, lecz jest maksymalna w pewnych punktach i minimalna w innych. Takie zjawisko nazywa się interferencją.
Ze względów historycznych obraz natężeń wytworzony przez nakładające się przyczynki ze
skończonej liczby dyskretnych, spójnych źródeł zwany jest zwykle obrazem interferencyjnym, a
obraz natężeń wytworzony przez nakładające się przyczynki z „ciągłego” rozkładu spójnych źródeł, zwany jest zwykle obrazem dyfrakcyjnym.
Za dużą odległość szczeliny od ekranu uważa się taką, która spełnia warunek
Lλ >> ( 12 D cos θ) 2
Lλ >> D2
praktycznie
(1)
gdzie L – odległość szczeliny od ekranu
D – szerokość szczeliny
λ − długość fali świetlnej padającej na szczelinę.
Warunki do wystąpienia dyfrakcji Fraunhofera można zrealizować w laboratorium, używając jako
źródła światła lasera i soczewki skupiającej (jeśli nie jest spełniony warunek (1)), która sprawia, że
fale płaskie opuszczające otwór dyfrakcyjny skupiają się w punkcie P. Przedmiotem dalszych
rozważań będzie tylko dyfrakcja Fraunhofera.
V. Dyfrakcja na pojedynczej szczelinie
Rysunek 2 przedstawia szczelinę o szerokości D podzieloną na N równoległych pasków o szerokości ∆x. Każdy pasek jest źródłem fal kulistych Huygensa i wytwarza określone zaburzenie falowe w punkcie P, którego położenie na ekranie można opisać za pomocą kąta θ.
ekran
B
∆x
B
P
θ
∆x
∆x sin θ
θ
D
Po
θ
soczewka
Rys.2 Szczelina o szerokości D podzielona na N pasków każdy o szerokości ∆x.
2
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Jeżeli paski są dostatecznie wąskie, to wszystkie punkty na pasku mają w zasadzie te same długości dróg optycznych do punktu P, a zatem całe światło z danego paska po dotarciu do P będzie
miało tę samą fazę. Amplitudy ∆Eo natężenia pola elektrycznego w punkcie P pochodzące z różnych pasków można przyjąć za jednakowe, jeśli kąt θ nie jest zbyt duży. Natężenie pola elektrycznego E charakteryzuje zaburzenie falowe docierające do danego punktu ekranu.
Zaburzenia falowe pochodzące od sąsiednich pasków mają stałe różnice faz ∆ϕ dane wzorem
różnica fazy
2π
=
różnica drogi
λ
czyli
∆ϕ =
2π
∆x sin θ
λ
(2)
(różnica drogi = ∆x⋅sinθ).
Znajdźmy amplitudę Eθ wypadkowego zaburzenia falowego dla różnych wartości ∆ϕ (tj. dla różnych punktów P na ekranie odpowiadających różnym wartościom θ). W tym celu przedstawiamy
poszczególne zaburzenia za pomocą odpowiednich wektorów i obliczamy amplitudę wypadkowego wektora.
α
α
ϕ
R
Rys.3 Konstrukcja, która służy do
obliczenia natężenia fali w
pewnym punkcie ekranu w
przypadku dyfrakcji na jednej
szczelinie.
R
Eθ
ϕ
∆Eo
Eo
Krzywa na rys.3 utworzona jest z wektorów, przedstawiających amplitudy zaburzeń falowych,
jakie dochodzą do dowolnego punktu na ekranie odpowiadającego dowolnemu kątowi θ. Jeśli
szczelinę podzielimy na nieskończoną ilość pasków o szerokości dx, to krzywa z rys.3 będzie zbliżała się do łuku koła, którego promień R pokazany jest również na rysunku. Długość tego łuku
wynosi Eo, czyli równy jest amplitudzie w środku obrazu dyfrakcyjnego, gdyż w środku tego obrazu wszystkie zaburzenia falowe są zgodne w fazie i łuk ten staje się linią prostą.
Kąt ϕ w dolnej części rysunku 3 jest więc różnicą fazy między nieskończenie małymi wektorami leżącymi na lewym i na prawym krańcu łuku Eo. Oznacza to, że ϕ jest różnicą fazy między
promieniami wychodzącymi z prawej i lewej strony szczeliny na rys.2 (rysunek przedstawia przekrój poziomy).
Z rozważań geometrycznych wynika, że
E θ = 2R sin 12 ϕ
(3)
W mierze łukowej kąt ϕ wynosi, jak widać z rysunku 3
E
E
ϕ= o
⇒ R= o
R
ϕ
Stąd otrzymujemy
3
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
E o sin 12 ϕ
(4)
1
ϕ
2
Ponieważ ϕ jest różnicą faz między promieniami wychodzącymi z dwu krańców, a różnica długości tych promieni wynosi D sin θ , więc (wzór (2))
2π
ϕ=
D sin θ
λ
Wyrażenie (4) można zapisać w postaci
sin α
Eθ = Eo
(5)
α
gdzie
1
πD sin θ
α= ϕ=
(6)
2
λ
Natężenie światła Iθ jest proporcjonalne do kwadratu amplitudy Eθ natężenia pola elektrycznego
czyli
Eθ =
 sin α 
Iθ = Io 

 α 
2
(7)
Wyrażenie (7) przyjmuje wartość minimalną dla
α = ± nπ
n = 1, 2, 3, …
Uwzględniając (6) otrzymujemy warunek na minima dyfrakcyjne
D ⋅ sin θ = ± nλ
n = 1, 2, 3, …
(8)
Dla małych kątów sin θ ≈ θ i wówczas położenie pierwszego minimum dyfrakcyjnego określone
jest przez zależność
λ
θ=±
(8a)
D
Znajdźmy położenia i natężenia dalszych maksimów dyfrakcyjnych. W przybliżeniu leżą
one w środku między sąsiednimi minimami a więc w punktach dla których
1

(9)
α ≈ ± n +  π
2

tzn. (po uwzględnieniu (6))
π
1
1


(10)
Dsinθ ≈ ± n + π ⇒
Dsinθ ≈ ± n + λ
λ
2
2


Podstawiając (9) do równania (7) otrzymamy w rezultacie
I(θ)
1
=
gdyż
sin 2 (n + 12 )π = 1
(11)
1 2 2
Io
(n + 2 ) π
Stąd otrzymujemy, że dla n = 1, 2, 3, … stosunek I(θ)/Io = 0,045, 0,016, 0,0083 itd. A więc natężenia maksimów bardzo szybko maleją.
Rysunek 4 pokazuje krzywe Iθ dla różnych wielkości stosunku D/λ. Obraz staje się coraz bardziej
wąski, gdy D/λ wzrasta (przy λ = const. odpowiada to szerszej szczelinie).
4
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Rys.4
VI. Dyfrakcja na podwójnej szczelinie
Schemat doświadczenia dyfrakcji na dwóch szczelinach przedstawia rysunek 5. Równoległa
wiązka światła z lasera 1 (padająca fala płaska) oświetla przesłonę z bardzo wąskimi szczelinami
S1 i S2.
Szerokość każdej szczeliny wynosi D, a odległość między ich środkami jest d. Zgodnie z zasadą
Huygensa, powierzchnia każdej szczeliny staje się źródłem wtórnych fal tj. światło ulega dyfrakcji
na każdej szczelinie. Ugięte fale są spójne, ponieważ powstały z czoła padającej fali płaskiej i w
wyniku interferencji na ekranie 3 możemy obserwować obraz interferencyjny (przy spełnieniu
warunku (1)).
5
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
d
θ
1
laser
∆ = d⋅⋅sinθ
θ
P
2
przesłona
3
ekran
r1
r2
S1
θ
Po
S2
θ
L
Rys.5 Dyfrakcja na dwóch szczelinach
Załóżmy, że składowe pola elektrycznego dwu fal wychodzących ze szczelin S1 i S2 zmieniają się w czasie w punkcie P następująco
E1 = E o sin ωt
E 2 = E o sin(ωt + ϕ′)
(12)
gdzie ω (= 2πν) jest częstością kołową fal, ϕ′ − różnicą faz między nimi wynikającą z różnicy
dróg optycznych. Zauważmy, że ϕ′ zależy od położenia punktu P, które z kolei przy ustalonej
geometrii doświadczenia, opisywane jest przez kąt θ (rys. 5). Przyjmijmy też, że szczeliny są tak
wąskie, że światło ugięte na każdej z nich oświetla środkową część ekranu równomiernie. Znaczy
to, że Eo w pobliżu środka ekranu nie zależy od położenia punktu P, a zatem od θ.
Wypadkowe natężenie pola w punkcie P jest równe
E = E1 + E 2 = E o sin ωt + E o sin(ωt + ϕ′)
(13)
Po wykonaniu odpowiednich przekształceń trygonometrycznych otrzymamy
E = E θ sin(ωt + β)
(14)
gdzie Eθ jest amplitudą wypadkowego natężenia pola, która jest równa
E θ = 2E o cos 12 ϕ′ = 2E o cos β
β=
1
ϕ′
2
(15)
(16)
(przekształcenia prowadzące do zależności (15) można znaleźć w D. Halliday, R. Resnik – Fizyka,
tom 1, rozdział 19-7 Interferencja fal)
Różnica fazy ϕ′ wiąże się z różnicą dróg promieni r1 i r2 (rys.5), która wynosi ∆ = d sin θ .
Z podobnej relacji jak w przypadku wzoru (2) można znaleźć różnicę fazy ϕ′
2π
ϕ′ =
d sin θ
(17)
λ
6
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
1
π
ϕ′ = d sin θ
(17a)
2
λ
Ponieważ natężenie I fali płaskiej i monochromatycznej jest proporcjonalne do kwadratu amplitudy, to dla powstałej fali ugiętej mamy
β=
I = I θ = kE θ2 = k 4E o2 cos 2 12 ϕ′
(18)
gdzie k jest współczynnikiem proporcjonalności.
Gdyby ekran oświetlała tylko jedna szczelina natężenie fali wynosiłoby
I1 = I 2 = kE o2 = Io
Uwzględniając ostatnią zależność wyrażenie (18) można przedstawić w postaci
2 1
2 1
′ int
′
Iint
θ = 4 I o cos 2 ϕ = I m cos 2 ϕ
(18a)
Z zależności (18a) wynika, że natężenie fali wypadkowej w maksimach od dwu wąskich szczelin
jest czterokrotnie większe od tego, jakie wytworzyłaby pojedyncza szczelina.
Maksima interferencyjne wystąpią dla tych kątów, dla których cos 2 12 ϕ′ we wzorze (18a) wynosi
1, czyli
1
ϕ′ = ± nπ
2
Uwzględniając (17) otrzymujemy warunek na maksima interferencyjne zwane głównymi
d sin θ = ± nλ
n = 0, 1, 2, …
(19)
Dla zakresu małych kątów sin θ ≈ θ wówczas położenie maksimów wyznacza zależność
λ
θ = ±n
(19a)
d
Minima wystąpią dla tych kątów, dla których 12 ϕ′ = ±(n + 12 )π , czyli
1

n = 0, 1, 2, …
(20)
d sin θ = ± n + λ ,
2

a dla sin θ ≈ θ mamy
1λ

(20a)
θ = ± n + 
2d

Ze względu na to, że fale uginające się na każdej ze szczelin dają na ekranie pod różnymi
kątami θ drgania o różnych amplitudach (gdy nie jest spełniony warunek wąskich szczelin, D <<λ)
natężenie światła w maksimach interferencyjnych będzie zależało od położenia na ekranie. Aby to
uwzględnić trzeba wziąć pod uwagę wygląd obrazu dyfrakcyjnego pojedynczej szczeliny o szerokości D (patrz punkt V, wzór (7)). Rzeczywisty rozkład natężenia światła na ekranie otrzymamy,
θ
gdy stałą amplitudę Iint
m w równaniu (18a) zastąpimy zmienną amplitudą I m , której zależność od
kąta θ dana jest równaniem (7). Otrzymamy wówczas następujące wyrażenie na wypadkowe natężenie obserwowane na ekranie
2
θ
m
Iθ = I cos
2 1
2
 sin 1 ϕ 
ϕ′ = I m  1 2  cos 2 12 ϕ′
 2ϕ 
(21)
2π
2π
d sin θ , ϕ =
D sin θ .
λ
λ
W ostatnim wzorze (21) opuszczono wskaźnik związany z interferencją (int).
gdzie ϕ′ =
7
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Czynnik cos 2 12 ϕ′ zwany czasem interferencyjnym daje szybką zależność natężenia od kąta θ,
charakterystyczną dla dwu szczelin. Czynnik (sin 12 ϕ / 12 ϕ) 2 daje modulację związaną z szerokością
szczeliny (tzw. czynnik dyfrakcyjny). Efekt modulacji pokazuje rysunek 6.
∆θinf
Iθ
a)
D=λ
0
θ
∆θinf
Iθ
b)
D = 5λ
0
θ
∆θdyf
Iθ
c)
D = 10λ
θ
0
Rys.6 Rozkład natężeń światła w obrazach interferencyjnych dla układu dwóch szczelin
(różne szerokości pojedynczych szczelin). Odległość wzajemna d szczelin na rysunkach a), b), c) jest taka sama. Linią przerywaną zaznaczono rozkład natężenia w płaszczyźnie obrazu, pochodzący od jednej szczeliny (gdy zasłonić drugą szczelinę).
W zakresie małych kątów θ, odległość kątowa między dwoma pierwszymi minimami dyfrakcyjnymi leżącymi po prawej i lewej stronie punktu 0 (patrz rys.6 i wzór (8a)) wynosi
2λ
∆θ = ∆θdyf = θ1 − θ−1 =
(22)
D
W płaszczyźnie ekranu odpowiadająca kątowi ∆θ dyf odległość liniowa ∆x wynosi
2λ
L
D
gdzie L jest odległością ekranu od szczelin.
∆x =
(22a)
8
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Zerowe maksimum dyfrakcyjne jest tym szersze im węższa jest szczelina oraz im większa jest
długość fali świetlnej.
Wykorzystując zależność (19a) otrzymujemy szerokość kątową maksimów głównych (interferencyjnych)
λ
∆θint = θ n − θn −1 =
(23)
d
Jeśli przez ∆x ′ oznaczymy odległość liniową na ekranie między sąsiednimi maksimami (lub minimami), to będzie ona równa
λ
∆x′ = L
(23a)
d
Między dwoma pierwszymi minimami dyfrakcyjnymi powstanie k maksimów interferencyjnych
∆x ∆θ dyf 2d
k=
=
=
(24)
∆x ′ ∆θ int
D
Jeżeli n–te minimum interferencyjne pokrywa się z pierwszym minimum dyfrakcyjnym tzn.,
że mamy
θ1dyf = θint
min, n
θ1dyf
1λ
λ 
= n + 
D 
2d
− położenie kątowe pierwszego minimum dyfrakcyjnego,
θint
min, n − położenie kątowe minimum głównego n–tego rzędu,
to wówczas liczba zaobserwowanych maksimów interferencyjnych wyrażona przez stosunek odległości dwóch szczelin i ich szerokość lub przez n-ty rząd maksimum interferencyjnego wyniesie
(przy uwzględnieniu wzoru (24))
2d
k=
= 2n + 1
(25)
D
W ogólnym przypadku relacja podająca związek między szerokością D pojedynczej szczeliny,
odległością d szczelin i obserwowaną liczbą k maksimów interferencyjnych w obszarze głównego
maksimum dyfrakcyjnego nie jest dana równością (25). Stosunek 2d/D może być bowiem dowolną liczbą, niekoniecznie całkowitą i nieparzystą. Znając z obserwacji liczbę maksimów k, stosunek
2d/D można tylko oszacować:
2d
k−2 <
≤k
(26)
D
VI. Układ pomiarowy i metoda pomiarów.
Zestaw do ćwiczenia składa się ze źródła światła spójnego (laser), z zestawu szczelin pojedynczych i podwójnych, ekranu (patrz rys. 7).
Płytka ze szczelinami jest umieszczana w uchwycie znajdującym się na koniku na ławie
optycznej. Obraz interferencyjny obserwuje się na ekranie.
Przy pomocy zestawu doświadczalnego z rysunku 7 można wyznaczyć :
1) długość fali λ światła laserowego,
2) liczbę k maksimów interferencyjnych występujących w obrębie głównego maksimum dyfrakcyjnego,
3) szerokość D pojedynczej szczeliny.
9
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
n′
Rys. 7 Układ pomiarowy z laserem i ekranem.
ad 1. Długość fali λ
Ze wzoru (23) odległość kątowa pojedynczego maksimum interferencyjnego wynosi
λ
∆θint =
(27)
d
Z drugiej strony ta odległość kątowa może być obliczona z zależności
∆θn ′
∆θint =
k′ − 1
gdzie ∆θn ′ jest odległością kątową między skrajnymi maksimami rzędu ± n′ , między którymi
dokonuje się pomiarów ( n′ ≤ n ),
k′ − liczba maksimów występujących w obrębie mierzonego odcinka ekranu ∆x n ′ . Z reguły liczba k′ nie jest równa maksymalnej liczbie obserwowanych maksimów k),
∆x n ′ − odległość liniowa między skrajnymi maksimami, dla których dokonywano pomiaru
odległości (rys.7 i rys.8b).
∆x n ′
Ponieważ ∆θ n ′ =
, to
L
∆x n ′
∆θint =
(28)
L ⋅ (k′ − 1)
Ze wzorów (27), (28) wynika równość ich prawych stron, a stąd dostaniemy
λ=
d ⋅ ∆x n ′
.
L ⋅ (k′ − 1)
(29)
ad 2. Liczba maksimów k
Obserwowana liczba maksimów zawsze będzie liczbą nieparzystą. Gdy wszystkie maksima
mają równą szerokość, to wartość stosunku szerokości D szczeliny i wzajemnej odległości d spełnia warunek (25):
10
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
2d
=k
gdzie k = 3, 5, 7, ….
D
Stosunek 2d/D może być jednak dowolną liczbą rzeczywistą większą od 1 i wówczas liczbę oczekiwanych maksimów ustalimy w sposób następujący. Oznaczmy część całkowitą stosunku 2d/D
przez p. Wówczas:
2d
a) Jeśli stosunek
jest równy dokładnie całkowitej nieparzystej liczbie (3, 5, 7..), to tyle równej
D
szerokości maksimów interferencyjnych spodziewamy się zaobserwować (gdy ta liczba jest
równa 1, to dwie szczeliny równej szerokości stanowią jedną szczelinę o szerokości 2D).
b) Jeśli część całkowita p jest liczbą nieparzystą (czyli p = 2n+1 dla n = 0, 1, 2, 3,…), ale istnieje
również część ułamkowa stosunku, to liczba spodziewanych maksimów jest równa k = p + 2 .
c) Jeśli część całkowita p jest liczbą parzystą (czyli p = 2n dla n = 1, 2, 3,…), to liczba oczekiwanych maksimów wynosi k = p + 1.
W przypadkach b) i c) krańcowe prawe i lewe maksima mają szerokość mniejszą niż pozostałe
(patrz Uzupełnienie strona 14).
ad 3. Szerokość D pojedynczej szczeliny
Ze wzoru (22) wynika, że
2λ
D
Z drugiej strony szerokość zerowego maksimum dyfrakcyjnego jest równa:
∆x
∆θdyf =
L
Stąd
∆x 2λ
2⋅λ⋅L
=
⇒ D=
L
D
∆x
∆θdyf =
(30)
VII. Wykonanie ćwiczenia
1. Włożyć płytkę z 4 pojedynczymi szczelinami o znanych szerokościach D w odpowiedni uchwyt
umieszczony na koniku na ławie optycznej. Oświetlić szczelinę światłem lasera, regulując w
razie konieczności położenie szczeliny względem wiązki światła laserowego (w poziomie i w
pionie).
Opis użytych płytek ze szczelinami:
NO SLITS – liczba szczelin (1 lub 2),
SLIT WIDTH – szerokość szczeliny (w tekście instrukcji jest to D),
SLIT SPACE – odległość szczelin (w tekście instrukcji jest to d).
2. Zmierzyć na ekranie odległość ∆x między dwoma minimami leżącymi po obu stronach zerowego maksimum dyfrakcyjnego dla każdej z czterech pojedynczych szczelin (rys.7 i rys.8a). Wyniki pomiarów zapisać w tabeli 1.
Tabela 1
Szczelina A Szczelina B
D = 0,02 mm D = 0,04 mm
Szczelina C
D = 0,08 mm
Szczelina D
D = 0,16 mm
Odległość
liniowa ∆x
[mm]
3. Zmierzyć odległość L ekranu od szczelin.
11
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
4. Włożyć płytkę z 4 układami szczelin podwójnych (układy szczelin podwójnych na płytce oznaczono literami A, B, C, D). Najlepiej nie zmieniać odległości L ekranu od szczelin (pojemnika
na szczeliny).
5. Policzyć liczbę kdośw wszystkich (dobrze i słabo widocznych) maksimów interferencyjnych
występujących w obrębie zerowego maksimum dyfrakcyjnego dla każdego układu szczelin podwójnych (rys 8b). Tę informację proponuje się zapisać w pierwszym wierszu tabeli 2 w formie:
k równej szerokości + 2 wąskie (lub bardzo wąskie).
Jeśli nie zmieniono odległości L ekranu od szczelin, to nie zachodzi potrzeba pomiaru tej odległości ponownie. W przeciwnym przypadku trzeba zmierzyć nową odległość L.
I
a)
Rys.8 a) Obraz dyfrakcyjny dla pojedynczej szczeliny o szerokości
D,
b) układ maksimów interferencyjnych obserwowanych na
ekranie dla dwu szczelin o jedx
nakowych szerokościach D.
∆x
∆x n ′
b)
− n′
+ n′
x
0
6. Zmierzyć dla każdego układu szczelin podwójnych odległość liniową ∆x n ′ między skrajnymi
dobrze widocznymi maksimami rzędu ± n′ (w obrębie zerowego maksimum dyfrakcyjnego).
Policzyć liczbę k′ maksimów występujących w obrębie mierzonej odległości ∆x n ′ .
Wyniki zapisać w tabeli 2.
Tabela 2
Układ A
dwu szczelin
D = 0,04 mm
d = 0,250 mm
Układ B
dwu szczelin
D = 0,04 mm
d = 0,500 mm
Układ C
dwu szczelin
D = 0,08 mm
d = 0,250 mm
Układ D
dwu szczelin
D = 0,08 mm
d = 0,500 mm
Liczba maksimów kdośw
Odległość
liniowa ∆x n ′
[mm]
Liczba maksimów k′
12
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
VIII. Opracowanie wyników.
1. Obliczyć długość fali λ światła użytego w doświadczeniu ze wzoru (29). Obliczenia wykonać
dla każdego układu szczelin podwójnych i obliczyć wartość średnią λ . Do obliczeń wykorzystać odległość szczelin d, odległość L ekranu od szczelin oraz wartości ∆x n ′ , k′ z tabeli 2.
Porównać otrzymaną wartość długości fali z długością fali podaną dla użytego światła laserowego.
2. Porównać liczbę maksimów interferencyjnych, które pojawiają się w obrębie zerowego maksimum dyfrakcyjnego (kdośw w tabeli 2), z liczbą wynikającą z analizy ilorazu 2d/D (p-kt VI, podpunkt ad.2) Liczba maksimów k).
3. Obliczyć szerokość D pojedynczej szczeliny dla każdej z czterech szczelin korzystając ze wzoru
(30). Do obliczenia szerokości D wykorzystać wartość długości fali podaną dla użytego światła
laserowego, odległość L oraz wartości ∆x zapisane w tabeli 1.
Porównać otrzymane wartości D z umieszczonymi przy szczelinach i sformułować wnioski.
4. Porównać obraz otrzymywany na ekranie przez układ szczelin podwójnych A z obrazem układu
C oraz układ B z D (różne szerokości szczelin D, takie same ich odległości d). Porównać także
obrazy układu A i B oraz C i D (takie same szerokości szczelin D, różne odległości d) i sformułować wnioski.
5. Obliczyć niepewność wyznaczenia długości fali λ:
 ∆(∆x n ′ ) ∆L ∆k′ 

∆λ = ± λ
+
+
L k′ − 1 
 ∆x n ′
Niepewność wyznaczenia d przyjęto równą 0. Ocenić niepewność ∆(∆x n′ ) , ∆L, ∆k′ .
6. Obliczyć niepewność wyznaczenia szerokości D szczelin:
 ∆L ∆(∆x) ∆λ 
∆D = ± D
+
+

∆x
λ 
 L
Długość fali światła laserowego użytego w ćwiczeniu wynosi: λ = 632,8 nm.
Niepewność jaką jest obarczona podana długości fali światła lasera przyjąć równą:
∆λ = ∆tλ = 1,0 nm.
Uwaga
Niepewnościami obarczone są również wyniki zaczerpnięte z literatury lub tablic fizycznych.
Jeśli brak jest jakiejkolwiek informacji o niepewności, przyjmujemy, że niepewność tablicowa ∆tλ jest równa 10 jednostkom ostatniego miejsca dziesiętnego.
UWAGA
Laser włączać tylko na czas przeprowadzania pomiarów.
Nie oświetlać oczu światłem laserowym.
13
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
Uzupełnienie
Iθ
2d
=7
D
a)
θ
0
Iθ
b)
2d
=8
D
θ
0
Iθ
2d
=9
D
c)
θ
0
Rys.9 Rozkład natężeń światła dla układu dwóch szczelin. Na rysunkach a), b), c)
szerokość szczelin D jest taka sama, natomiast odległość wzajemna d jest
różna.
14
I PRACOWNIA FIZYCZNA
Ćwiczenie O-19
1. Gdy stosunek 2d/D jest dokładnie równy 7 (rys. 8a), to wówczas pierwsze minimum dyfrakcyjne pokrywa się z czwartym minimum interferencyjnym (n = 3).W obrębie głównego maksimum dyfrakcyjnego mieści się dokładnie k = 7 maksimów interferencyjnych równej szerokości.
2. Gdy 2d/D rośnie od 7 do 8, pojawiają się dodatkowo dwa skrajne maksima (prążki). Będzie ich
więc teraz 9 szt. Początkowo te dwa nowe będą wąskie (a więc słabo widoczne) a przy stosunku 2d/D = 8 ich szerokość wyniesie połowę standardowej szerokości maksimów (rys. 8b).
3. Gdy 2d/D rośnie dalej od 8 do 9 obserwuje się w dalszym ciągu k = 9 maksimów (prążków),
przy czym dwa skrajne stają się coraz szersze.
4. Gdy 2d/D = 9 (rys.9c) skrajne prążki osiągają szerokość pozostałych maksimów. Widocznych
jest k = 9 maksimów jednakowej szerokości. Teraz pierwsze minimum dyfrakcyjne pokrywa
się z piątym minimum interferencyjnym (n = 4).
Obserwowana liczba maksimów zawsze będzie liczbą nieparzystą. Gdy wszystkie maksima
mają równą szerokość, to wartość stosunku szerokości D szczeliny i wzajemnej odległości d spełnia warunek
2d
=k
gdzie k = 3, 5, 7, ….
D
Z analizy przedstawionego przykładu wynika, że możemy zaobserwować taką samą liczbę
maksimów (chociaż nie wszystkie są jednakowej szerokości) przy różnym stosunku 2d/D. Z ilości
obserwowanych maksimów nie można więc uzyskać jednoznacznej informacji o wartości stosunku 2d/D. Natomiast z analizy wartości tego stosunku można uzyskać informacje o liczbie maksimów możliwych do zaobserwowania (patrz punkt VI, ad 2. Liczba maksimów k, przypadki a),
b), c)).
Przykład 1
d = 0,26 mm, D = 0,04 mm
2d 2 ⋅ 0 ,26mm
=
= 13,0 k = 13 (przypadek a)).
D
0 ,04mm
Przykład 2
d = 0,225 mm, D = 0,04 mm
2d 2 ⋅ 0,225mm
=
= 11,25, p = 11, k = p + 2 = 13 (przypadek b)).
D
0,04mm
Przykład 3
d = 0,20 mm, D = 0,04 mm
2d 2 ⋅ 0 ,20mm
=
= 10,0 p = 10, k = p +1 = 11 (przypadek c)).
D
0 ,04mm
15
I PRACOWNIA FIZYCZNA