postac standardowa PL

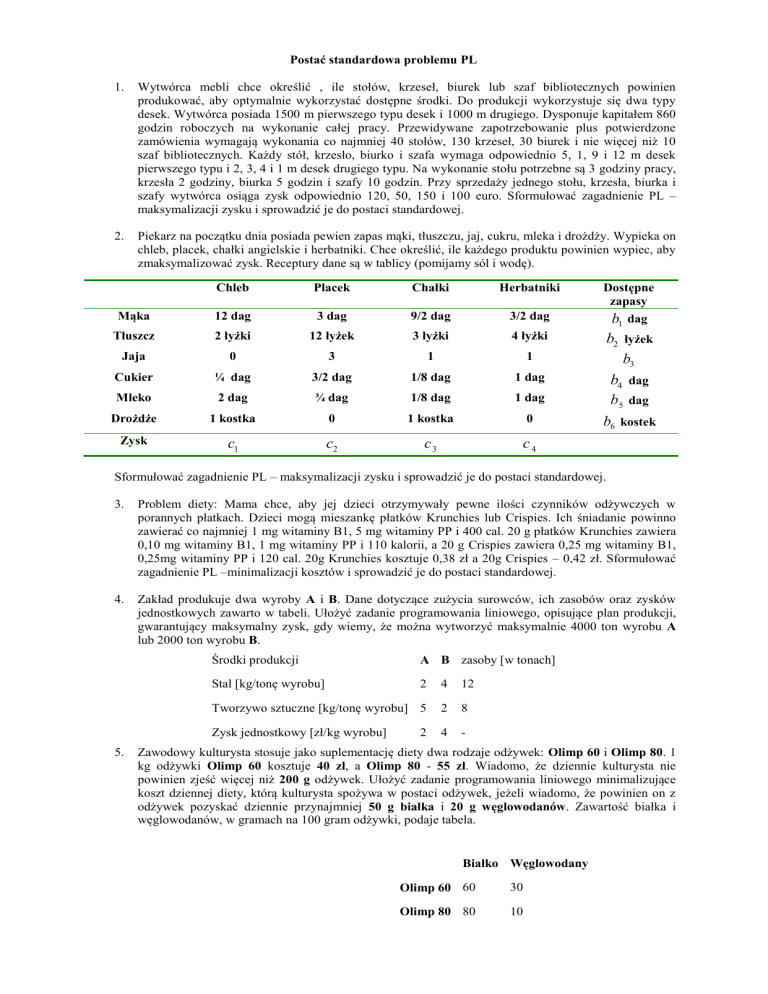
Postać standardowa problemu PL
1.
Wytwórca mebli chce określić , ile stołów, krzeseł, biurek lub szaf bibliotecznych powinien
produkować, aby optymalnie wykorzystać dostępne środki. Do produkcji wykorzystuje się dwa typy
desek. Wytwórca posiada 1500 m pierwszego typu desek i 1000 m drugiego. Dysponuje kapitałem 860
godzin roboczych na wykonanie całej pracy. Przewidywane zapotrzebowanie plus potwierdzone
zamówienia wymagają wykonania co najmniej 40 stołów, 130 krzeseł, 30 biurek i nie więcej niż 10
szaf bibliotecznych. Każdy stół, krzesło, biurko i szafa wymaga odpowiednio 5, 1, 9 i 12 m desek
pierwszego typu i 2, 3, 4 i 1 m desek drugiego typu. Na wykonanie stołu potrzebne są 3 godziny pracy,
krzesła 2 godziny, biurka 5 godzin i szafy 10 godzin. Przy sprzedaży jednego stołu, krzesła, biurka i
szafy wytwórca osiąga zysk odpowiednio 120, 50, 150 i 100 euro. Sformułować zagadnienie PL –
maksymalizacji zysku i sprowadzić je do postaci standardowej.
2.
Piekarz na początku dnia posiada pewien zapas mąki, tłuszczu, jaj, cukru, mleka i drożdży. Wypieka on
chleb, placek, chałki angielskie i herbatniki. Chce określić, ile każdego produktu powinien wypiec, aby
zmaksymalizować zysk. Receptury dane są w tablicy (pomijamy sól i wodę).
Chleb
Placek
Chałki
Herbatniki
Mąka
12 dag
3 dag
9/2 dag
3/2 dag
Tłuszcz
2 łyżki
12 łyżek
3 łyżki
4 łyżki
Jaja
0
3
1
1
Cukier
¼ dag
3/2 dag
1/8 dag
1 dag
Mleko
2 dag
¾ dag
1/8 dag
1 dag
Drożdże
1 kostka
0
1 kostka
0
Zysk
c1
c2
c3
c4
Dostępne
zapasy
b1 dag
b2 łyżek
b3
b4 dag
b5 dag
b6 kostek
Sformułować zagadnienie PL – maksymalizacji zysku i sprowadzić je do postaci standardowej.
3.
Problem diety: Mama chce, aby jej dzieci otrzymywały pewne ilości czynników odżywczych w
porannych płatkach. Dzieci mogą mieszankę płatków Krunchies lub Crispies. Ich śniadanie powinno
zawierać co najmniej 1 mg witaminy B1, 5 mg witaminy PP i 400 cal. 20 g płatków Krunchies zawiera
0,10 mg witaminy B1, 1 mg witaminy PP i 110 kalorii, a 20 g Crispies zawiera 0,25 mg witaminy B1,
0,25mg witaminy PP i 120 cal. 20g Krunchies kosztuje 0,38 zł a 20g Crispies – 0,42 zł. Sformułować
zagadnienie PL –minimalizacji kosztów i sprowadzić je do postaci standardowej.
4.
Zakład produkuje dwa wyroby A i B. Dane dotyczące zużycia surowców, ich zasobów oraz zysków
jednostkowych zawarto w tabeli. Ułożyć zadanie programowania liniowego, opisujące plan produkcji,
gwarantujący maksymalny zysk, gdy wiemy, że można wytworzyć maksymalnie 4000 ton wyrobu A
lub 2000 ton wyrobu B.
5.
Środki produkcji
A B zasoby [w tonach]
Stal [kg/tonę wyrobu]
2
4
12
Tworzywo sztuczne [kg/tonę wyrobu] 5
2
8
Zysk jednostkowy [zł/kg wyrobu]
4
-
2
Zawodowy kulturysta stosuje jako suplementację diety dwa rodzaje odżywek: Olimp 60 i Olimp 80. 1
kg odżywki Olimp 60 kosztuje 40 zł, a Olimp 80 - 55 zł. Wiadomo, że dziennie kulturysta nie
powinien zjeść więcej niż 200 g odżywek. Ułożyć zadanie programowania liniowego minimalizujące
koszt dziennej diety, którą kulturysta spożywa w postaci odżywek, jeżeli wiadomo, że powinien on z
odżywek pozyskać dziennie przynajmniej 50 g białka i 20 g węglowodanów. Zawartość białka i
węglowodanów, w gramach na 100 gram odżywki, podaje tabela.
Białko Węglowodany
Olimp 60 60
30
Olimp 80 80
10
6.
Pewien bank rozważa możliwość lokalizacji bankomatów w mieście tak, aby ułatwić dostęp do nich
swoim klientom. Proponowane lokalizacje oraz odpowiednie dzielnice, które każdy bankomat będzie
obsługiwał podaje tabelka.
Proponowana lokalizacja
Dzielnice
A
1,5,7
B
1,2,5
C
1,3,5,6
D
2,4
E
1,3,4
F
4,5,6
G
5,6,7
Sformułuj zadanie, które może zostać wykorzystane do znalezienia najmniejszej liczby bankomatów
pokrywających swoim zasięgiem wszystkie dzielnice miasta.
7. Na jeden produkt składają się dwa detale typu A i 5 detali typu B. Oba rodzaje wycinane są z takich
samych arkuszy blachy, przy czym jest 5 różnych sposobów cięcia (wykrojów?), które różnią się ilością
elementów obu typów, jakie z jednego arkusza się otrzyma. Oto tabelka:
Sposób cięcia
Detal
A
B
I
II
4
3
0
1
Mamy zamiar zrealizować zamówienie na 90
sformułować zagadnienie PL.
III
IV
V
2
1
0
3
4
5
kompletów minimalizując sumę arkuszy. Proszę
8.
Zakład otrzymał zamówienia na wykonanie 100 kompletów składających się z 3 detali. Detale są
wycinane z blachy. Stosowana technika cięcia pozwala na uzyskanie n różnych sposobów rozkroju
arkusza blachy. Wiadomo, że stosując j-ty sposób rozkroju (j=1,2,...,n) uzyskuje się z jednego arkusza
Sij sztuk i-tego detalu (i=1,2,3) oraz odpad b j (j=1,2,...,n) kg. Sformułuj problem, którego rozwiązanie
pozwala na wybór sposobów rozkroju dla 5 arkuszy tak, aby łączna ilość odpadów była jak
najmniejsza.
9.
Pewna poczta jest czynna w godzinach 8.00-20.00. Utrzymanie sprawnej organizacji pracy wymaga
zatrudnienia w godzinach 8.00-10.00 co najmniej 2 osób, w godzinach 10.00-16.00 co najmniej 6 osób
oraz w godzinach 16.00-20.00 co najmniej 2 osób. Ile co najmniej osób należy zatrudnić i w jakim
układzie , jeżeli czas pracy jednego zatrudnionego wynosi 8 godzin, a pracę można zaczynać o 8.00,
10.00 lub 12.00? Proszę sformułować zagadnienie PL dotyczące tego problemu.
10. Tartak posiada 9 belek o długości 2,1 m. Klient zamówił 3 elementy o długości 0,8 m, 4 elementy o
długości 0,9 m oraz 5 elementów o długości 1,1 m. Sposób polegający na wycięciu 2 elementów o
długości 0,9 może być zastosowany co najwyżej dwa razy.
a) Tartak minimalizuje wielkość powstałego w procesie cięcia odpadu. Proszę sformułować zagadnienie
PL rozstrzygające o wyborze sposobów cięcia belek.
b) Koszt zakupu jednej belki wynosi 200 zł, a cena sprzedaży elementów: 0,8m – 110 zł, 0,9 m – 120 zł,
1,1 m – 150 zł. Proszę sformułować zagadnienie PL rozstrzygające o wyborze sposobów cięcia belek,
jeżeli tartak maksymalizuje zysk.
( Zakładamy, ze możliwa będzie sprzedaż powyżej zamówienia. )
11. Zakład produkujący gwoździe otrzymuje drut o wymaganej grubości w 30- centymetrowych
kawałkach. Kawałki te cięte są na krótsze, odpowiadające długościom gwoździa, czyli 11, 8 i 5 cm.
Należy tak pociąć otrzymywane kawałki drutu, aby wyprodukować 12 000 gwoździ o długości 11 cm,
24 000 gwoździ o długości 8 cm i 27 000 gwoździ o długości 5 cm, minimalizując odpad. Proszę
sformułować zagadnienie PL.
12. Zakład produkuje dwa rodzaje soków: jabłkowy i wieloowocowy. Do wytworzenia jednego litra soku
potrzeba odpowiednio:
Rodzaj soku
Jabłkowy
Wieloowocowy
Cena (kg)
Jabłko (kg)
0,5
0,2
2 zł
Pomarańcz (kg)
0,2
4 zł
Truskawka (kg)
0,1
4 zł
cukier (kg)
0,25
0,2
2 zł
Cena (kg)
3 zł
4 zł
W ciągu tygodnia zakład może zmówić maksymalnie 150 kg jabłek, 100 kg pomarańczy, 40 kg
truskawek oraz 110 kg cukru.
a) Ile litrów soku jabłkowego, a ile wieloowocowego powinien produkować zakład by maksymalizować
zysk? Proszę sformułować zagadnienie PL i rozwiązać je metoda graficzną.
b) Który z warunków ograniczających jest nie istotny?
c) Czy rozwiązanie zadania zmieni się, gdy cena sprzedaży soku wieloowocowego wzrośnie do 5,75?
13. W pewnym zakładzie (elektrownia, gazownia lub pogotowie ratunkowe) z powodów technologicznych
konieczna jest stała obecność pracowników. Ze względu na zmienne natężenie realizowanego procesu
liczba niezbędnych pracowników ulega zmianie. Można ją określić dla czterogodzinnych przedziałów
czasu w czasie całej doby: godziny 0-4 – co najmniej 4 osoby, godziny 4-8 – co najmniej 18 osób, 8-12
– co najmniej 7, 12-16 – co najmniej 15, 16-20 – co najmniej 18, w przedziale 20-24 – co najmniej 6
osób. Pracownicy przychodzą do pracy tylko o określonych godzinach (0, 4, 8, 12, 16 lub 20), a po
przyjściu pozostają w pracy przez całą zmianę, która trwa równe 8 godzin.
Należy zbudować zadanie PL w celu uzyskania odpowiedzi na pytanie: jaka jest minimalna
liczba pracowników niezbędnych do obsługi procesu produkcyjnego w ciągu doby?