Fale elektromagnetyczne

Fale elektromagnetyczne
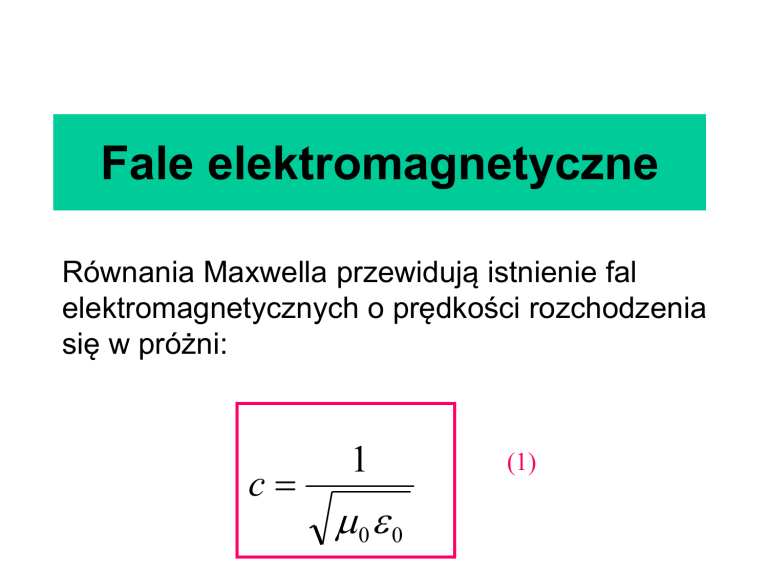
Równania Maxwella przewidują istnienie fal
elektromagnetycznych o prędkości rozchodzenia
się w próżni:
c
1
0 0
(1)
Równania Maxwella przewidują, że zmienne w
czasie pole magnetyczne indukuje wirowe pole
elektryczne i na odwrót, zmienne w czasie pole
elektryczne indukuje wirowe pole magnetyczne. Każda
zmiana w czasie pola elektrycznego wywoła powstanie
zmiennego pola magnetycznego, które z kolei wytworzy
zmienne pole pole elektryczne.
Ciąg wzajemnie sprzężonych pól
elektrycznych i magnetycznych stanowi falę
elekromagnetyczną.
Fale elektromagnetyczne możemy podzielić na
• stojące (np. wnęka rezonansowa) i
• bieżące - rozchodzące się wzdłuż linii przesyłowej lub w
wolnej przestrzeni.
Obwód LC
Przykład powstawania fal elektromagnetycznych.
Drganiom wytworzonym w elektrycznym obwodzie
LC (cewka, kondensator) towarzyszy okresowa zmiana
energii pola elektrycznego kondensatora w energię pola
magnetycznego cewki.
Jeżeli pominiemy straty na ciepło, to energia drgań
w obwodzie pozostanie stała.
Pole B
L
C
Do
generator
a drgań
Pole E
Obwód taki przekształcamy w następujący sposób: cewkę
redukujemy do prostoliniowego przewodu, okładki
kondensatora zmniejszamy, a przewody prostujemy. Pole
elektryczne i magnetyczne wypełnia teraz bardzo dużą
przestrzeń.
Przekształcanie zamkniętego obwodu
drgań w dipol elektryczny
E
B
Do
generatora
drgań
Przekształcony obwód ma
teraz większą zdolność
emitowania energii, stał się
obwodem otwartym.
Powstały obwód stanowi
dipol elektryczny o
momencie dipolowym
zależnym od czasu.
Jeżeli do prętów dipola doprowadzone zostanie napięcie
zmienne, to pręty będą się ładować okresowo ładunkiem
dodatnim i ujemnym. Zatem obwód taki staje się
oscylującym dipolem elektrycznym emitującym falę
elektromagnetyczną we wszystkich kierunkach.
Pole elektryczne dipola w czterech chwilach:
+q
+
-
-q
t=0
t = 1/8 T
+
-
t = 1/4 T
+
t = 3/8 T
z
P
x
O
Wykres biegunowy
natężenia fali
emitowanej przez dipol,
znajdujący się na osi z.
Długość odcinka OP jest
proporcjonalna do
natężenia fali
emitowanej w danym
kierunku.
Zmienne napięcie doprowadzone do z generatora powoduje
przepływ prądu wzdłuż dipola. Ładunki zbierające się na
końcach prętów dipola wytwarzają tam największe napięcia.
Drgania elektryczne rozchodzące się wzdłuż dipola dają w
wyniku falę stojącą. Fala emitowana przez dipol jest już
falą rozchodzącą się w przestrzeni (bieżącą). Fala ta jest
spolaryzowana, wektor E jest równoległy do osi dipola, B prostopadły.
Na podstawie wprowadzonych równań Maxwell wykazał, że
wzajemnie sprzężone pola elektryczne i magnetyczne
tworzą falę poprzeczną i obliczył prędkość fali. W fali
elekromagnetycznej wektory E i B są prostopadłe do siebie i
do kierunku rozchodzenia się fali.
Dla fali rozchodzącej się wzdłuż osi x zależność
natężenia pola B i E od czasu i położenia ma postać
następującą:
B = Bmsin(kx - t)
 - pulsacja,  = 2
k - liczba falowa
 - długość fali
T - okres drgań
 - częstotliwość
(2)
E = Em sin(kx -  t)
(3)
2
2
(4) kx   x (4a)
k

2 (6)
1
t
  (5) t 
T
T
Płaska fala elektromagnetyczna poruszająca się
w dodatnim kierunku osi x
dx
y
•

•


•••


•


•
• • •
  
• • •
•

•
c
x
z
E  z
B  y
h
c  x
Pola E i B są zgodne w fazach.
Prostokąt o wymiarach h i dx nie porusza się w przestrzeni. W
miarę przesuwania się fali strumień magnetyczny B będzie
się zmieniał, co spowoduje powstanie indukowanych pól
elektrycznych. To indukowane pola elektryczne, to składowe
elektryczne wytworzonej fali bieżącej. Zastosujmy prawo
Faradaya dla obwodu prostokąta o bokach h i dx (pł. xz).
 
d B
(7)
 E  dl   dt
 
 E  dl  ( E  dE )h  Eh  hdE
(8)
Strumień pola magnetycznego przechodzący przez
powierzchnię prostokąta (płaszczyzna xz) wynosi:
 B  Bhdx (9)
B jest wartością bezwzględną pola w
prostokącie
Różniczkowanie po czasie daje
dE
dB

dx
dt
(10)
Na podstawie prawa Faradaya w postaci (8 ) otrzymujemy
B (11)
hdE   hdx
dt
stąd
dE
dB

dx
dt
(12)
E
B

x
t
(13)
E(x,t) i B(x,t) są znane, więc równanie (13) można zapisać
jako
kEmcoskx  t   Bmcoskx  t  (14)
Em (15) ale 
czyli 
(16)
k

k
Bm
c
Oznacza to również, że związek słuszny jest dla
dowolnych wielkości pola E i B w danym momencie.
E  cB
(17)
Zastosujmy teraz prawo
Ampera w postaci:
 
d E
 B  dl  0 0 dt
(18)
Całkując to równanie po obwodzie prostokąta o bokach h
i dx w płaszczyźnie xy otrzymujemy:
 
 B  dl  B  dB h  Bh  hdB
(19)
Strumień pola elektrycznego przechodzący przez ten
prostokąt wynosi:
(20)
E  Ehdx
Różniczkując po czasie otrzymujemy:
d E
dE
 hdx
dt
dt
(21)
a więc równanie (18 )
można przepisać w postaci
B
E

  0 0
x
t
(22)
Korzystając z równań (14 ), (22 ) otrzymujemy:
 kBm coskx  t    0 0Em coskx  t 
(23)
stąd
Em
k

Bm  0 0
(24)
Eliminując Em/Bm otrzymamy:
c
1
0 0
c - prędkość światła w teorii
(1) elektromagnetyzmu. Maxwell
przewidział ten związek przed
odkryciem fal radiowych!
1
8 m
c
 3.0 10
7
12 2
2
4  10 T  m / A [8.9 10 C / N  m ]
s


Energia niesiona przez falę elektromagnetyczną
B
h•h = s
y
c
E
x
z
dx
Wyznaczmy energię
fali przechodzącą
przez pudełko o
objętości sdx, gdzie s
jest polem powierzchni
podstawy w
płaszczyźnie yz.
Przyjmujemy h = 1
W pewnej chwili energia dW zawarta w pudełku o objętości
sdx przenoszona przez falę elektromagnetyczną wynosi
dW = dWE + dWB = (uE + uB)sdx (25)
Energia
pola E
uE - gęstość pola E
Energia
pola B
uB - gęstość pola B
1
1 2 
2
dW    0 E 
B sdx
2 0
2

ale
E  cB
(26)
(17)
2
1

0 0c  1
1
E
dW    0 EcB 
B sdx 
EBsdx (28)
2μ0 c 
2 0 c
2
 0 0 c 2  1
Zgodnie z (1)
dx
oraz
dt 
c
dw
EBsdx
1
W
Energia przepływająca


EB [ 2 ]
dt  s μ cs dx μ0
m
przez jednostkową
0
(29) powierzchnię w
c
jednostkowym czasie.
dw
S
dts
(30)
 1  
S
EB
0
(31)
Energię tę oznaczono
następnie przez S i
wprowadzono
odpowiadający jej
wektor przepływu
energii zwany
wektorem Pointynga
Wielkość S jest wyrażona przez wartości chwilowe, więc
jest funkcją czasu.
Wektor S jest prostopadły do wektora E i do wektora B.
Wektor Pointynga pokazuje kierunek przenoszenia energii.
Z trzech wielkości występujących w równaniu (31), jedna
ma ściśle określoną wartość:
T m
 0  4π  10
A
7
pozostałe c i 0 są mierzalne.
Na podstawie równania (1) wykorzystuje się zmierzoną
dokładnie wartość prędkości światła
c = 2.99792458 • 108 m/s
do wyznaczania wartości 0.
Prędkość c, mimo że dotyczy wszystkich fal
elektromagnetycznych, nazywa się prędkością
światła.
W roku 1888 Heinrich Hertz przeprowadził po
raz pierwszy eksperyment, w którym były
wytwarzane i odbierane fale
elektromagnetyczne, dowodząc tym samym ich
istnienia i potwierdzając słuszność równań
Maxwella.
James Maxwell
Maxwell urodził się w 1831 r. w Edynburgu w
Szkocji. Był tzw. Cudownym dzieckiem; mając
zaledwie piętnaście lat przedstawił pracę
naukową w Edinburgh Royal Society. Uczęszczał
na uniwersytet w Edynburgu. Stopień naukowy
otrzymał na uniwersytecie w Cambridge. Był
żonaty, ale nie miał dzieci. Maxwell uważany jest
powszechnie za największego fizyka teoretyka w
okresie pomiędzy Newtonem i Einsteinem. Jego
wspaniała kariera zakończyła się przedwcześnie;
zmarł na raka w 1879 r., na krótko przed
czterdziestymi ósmymi urodzinami.
Hertz Heinrich Rudolf (1857-1894)
Kwantowe własności
promieniowania
Ciało doskonale czarne
Z doświadczeń wiadomo, że ciało ogrzane do
odpowiednio wysokiej temperatury zaczyna wysyłać
promieniowanie widzialne, jak również wiadomo, że ciało
ogrzane do temperatury wyższej promieniuje bardziej
intensywnie niż ciało o temperaturze niższej. Obserwacje i
dokładniejsze pomiary pozwalają na stwierdzenie, że wszystkie
ciała emitują promieniowanie elekromagnetyczne, które
nazywamy promieniowaniem cieplnym w każdej
temperaturze wyższej od zera bezwzględnego T > 0 K. Widmo
promieniowania cieplnego jest bardzo szerokie od zakresu
radiowego do rentgenowskiego, ale zakres najbardziej
intensywny zależy od temperatury. Teoretyczny opis
promieniowania cieplnego przeprowadza się dla
wyidealizowanego ciała zwanego ciałem doskonale czarnym.
Wyobraźmy sobie wnękę wydrążoną w dowolnym ciele,
połączoną z otoczeniem niewielkim otworem.
Promieniowanie padające na ten otwór i dostające się do
wnęki będzie ulegało wielokrotnemu odbiciu od ścianek
wnęki.
W wyniku strat zachodzących przy odbiciu,
promieniowanie zostanie prawie całkowicie pochłonięte nim
wiązka trafi z powrotem do otworu.
Model ciała doskonale
czarnego
Widmo promieniowania ciała doskonale czarnego
50
R jedn.
umowne
T1 > T2
T1
1 < 2
40
30
20
T2
10
0
1
1
2
2
3
 - długość fali
4
5
[μm]
Prawo Wiena
Pierwszą teorię ciała doskonale czarnego stworzył
Wien. Uważał on, że podobieństwo krzywych rozkładu
promieniowania cieplnego do maxwellowskiego rozkładu
prędkości cząsteczek gazu wynika stąd, że drgające
cząsteczki w gorącym ciele stałym mają rozkład prędkości
podobny do rozkładu Maxwella. Prędkościom tym powinny
odpowiadać odpowiednie termiczne przyspieszenia
cząsteczek. Ponieważ cząsteczki obdarzone są ładunkami
elektrycznymi, więc zgodnie z elektrodynamiką klasyczną
powinny emitować promieniowanie w trakcie
niejednostajnego ruchu. Na podstawie tego Wien dopasował
do krzywej doświadczalnej zdolności emisyjnej modelu ciała
doskonale czarnego wzór empiryczny (3) na rozkład
zdolności emisyjnej względem długości fali , analogiczny
do rozkładu Maxwella.
Zdolność emisyjna R zdefiniowana jest jako moc P
promieniowania wysyłanego z jednostki powierzchni s ciał
w jednostkowym przedziale długości fal .
P
R 
S  
(32)
Całkowita zdolność emisyjna R ciała jest to moc
promieniowania w całym zakresie długości fal, wysyłanego
z jednostki powierzchni ciała.

R   R d
(33)
0
Zdolność emisyjna podana przez Wiena
ma postać następującą:
 C2 

R  C1 exp  
 T 
5
(34)
T - temperatura
C1 i C2 odpowiednio
pierwsza i druga
stała emisyjna
Wartości stałych emisyjnych we wzorze Wiena dobrano
tak, że aby otrzymać dobrą zgodność w zakresie fal
krótkich. W zakresie fal długich obliczone na podstawie
wzoru (3) zdolności emisyjne były znacznie mniejsze od
wyników doświadczalnych.
Wzór Rayleigha-Jeansa
Uczeni ci rozpatrywali ciało doskonale czarne w postaci
wnęki mającej zwierciadlane ścianki. Wewnątrz takiej wnęki
powstają wówczas elektromagnetyczne fale stojące,
podobne do fal w strunie lub w rezonatorze akustycznym, w
którym obok drgania podstawowego występuje szereg
wyższych harmonicznych. Rayleigh i Jeans otrzymali
związek na liczbę fal powstałych w jednostce objętości
wnęki w zakresie długości fal od  do  + d o postaci:
dN   8
d

4
(35)
Każdej z tych fal można przypisać dwa stopnie swobody
i każdemu z nich przypisać energię kT/2, co oznacza, że
każdej fali odpowiada całkowita energia kT. Mnożąc
liczbę fal przypadających na jednostkę objętości przez
kT otrzymamy wzór Rayleigha-Jeansa:
R 
8

4
kT
(36)
gdzie k jest stałą
Boltzmanna
Wzór ten jest zgodny z fizyką klasyczną, ale w
zakresie fal krótkich dawał wyniki absurdalne,
niezgodne z danymi doświadczalnymi.
Prawo Plancka
Max Planck (1900) zwrócił uwagę, że gdyby wzór
Wiena zmienić w prosty sposób, dawałby wyniki zgodne
z doświadczeniem. Planck założył, że atomy ścian wnęki
(ciąła doskonale czarnego) zachowują się jak oscylatory
elektromagnetyczne, z których każdy ma
charakterystyczną częstotliwość drgań. Atomy te emitują
do wnęki i absorbują z niej energię elektromagnetyczną.
Własności powstałego promieniowania we wnęce
wynikają z własności oscylatorów, z którymi wnęka jest w
równowadze. Planck przyjął dwa istotne założenia:
1. Oscylator nie może mieć dowolnej energii, lecz
tylko energie dane wzorem:
E = nh
(37)
gdzie  oznacza częstotliwość oscylatora, h - stała
(zwana obecnie stałą Plancka, n - pewna liczba (liczba
kwantowa), która może przybierać tylko całkowite
wartości. Z równania tego wynika, że energia
oscylatorów musi być skwantowana. Późniejsze
odkrycia pokazały, że poprawny wzór na energię
oscylatora harmonicznego ma postać:
1

E   n   h
2

(38)
2. Oscylatory nie wypromieniowują energii w sposób
ciągły, lecz skokami czyli kwantami. Kwanty energii
są emitowane, kiedy oscylator przechodzi z jednego
do drugiego stanu energetycznego. Jeżeli n zmienia
się o jedność w równaniu (6), wypromieniowana
zostaje ilość energii dana wzorem:
E =  nh = h
(39)
Dopóki oscylator pozostaje w jednym ze swoich
stanów kwantowych, zwanych stacjonarnymi, dopóty
nie emituje ani nie absorbuje. Przy takich założeniach
widmowa zdolność emisyjna ciała doskonale
czarnego, podana przez Plancka ma postać
R 
2 c 2

h
5
e
hc
kT
(40)
1
Po scałkowaniu R względem  otrzymujemy
wyrażenie na zdolność emisyjną ciała doskonale
czarnego
2 5 k 4 4
R
T
3 2
15h c
(41)
Związek ( ) zapisuje się często w postaci
R  T4
(42)
Przy czym  = 5.67 • 10-8 W/m2 •K4. Jest to prawo
Stefana-Boltzmanna, które mówi, że
Całkowita zdolność emisyjna ciała doskonale
czarnego jest proporcjonalna do czwartej
potęgi jego temperatury bezwzględnej
Dla dowolnego ciała rzeczywistego emisja
promieniowania ma mniejszą wartość i można
wyrazić ją wzorem
R  A T 4
(43)
gdzie A oznacza zdolność absorpcyjną ciała. Dla ciała
doskonale czarnego A = 1, dla ciał rzeczywistych
0<A<1. Ciała doskonale odbijające A = 0.
Widmowa zdolność emisji R ma wartość
maksymalną dla pewnej długości fali max, którą
możemy obliczyć z warunku:
dR
0
d
(44)
Różniczkując to wyrażenie
dochodzimy do zależności:
max
b

T
(45) gdzie b = 2898 • 10-6 m • K
Wzór ten nazywa się prawem przesunięć Wiena:
Ze wzrostem temperatury maksimum
promieniowania ciała doskonale czarnego przesuwa
się w stronę fal krótszych.
Efekt taki obserwujemy jako zmianę barwy ciała, które
ogrzewamy do wysokiej temperatury.
Prawo przesunięć może być też wyprowadzone z wzoru (34).
Stała Plancka, wprowadzona w modelu ciała doskonale
czarnego, wyznaczona jest na podstawie efektu
fotoelektrycznego, potwierdzającego kwantową naturę
promieniowania. Wynosi ona:
h = 6.625 • 10-34 J • s
Doświadczalne dowody
kwantowej natury
promieniowania
Efekt fotoelektryczny:
a) zewnętrzny, b) wewnętrzny
Zjawisko fotoelektryczne zewnętrzne polega na
wybijaniu elektronów z powierzchni ciała stałego przez
promieniowanie. Zjawisko obserwowane jest w układzie
zawierającym bańkę próżniową z dwiema elektrodami. W
obwodzie zewnętrznym znajduje się źródło zasilania, miernik
prądu i miernik napięcia. Pod wpływem padającego na
katodę promieniowania można zaobserwować przepływ
prądu. Analiza zjawiska fotoelektrycznego obejmuje badanie
zależności natężenia od napięcia oraz wpływu częstotliwości
na przebieg zjawiska fotoelektrycznego. W zakresie napięć
hamujących przepływ prądu tylko te elektrony docierają do
anody, których energia kinetyczna jest większa od energii
pola elektrycznego. Przy pewnej wartości pola prąd zanika,
odpowiadające temu napięcie Uh nazywamy napięciem
hamującym. Możemy zauważyć że maksymalna energia
elektronów równa jest energii hamującego pola.
Ekmax = e Uh
(46)
I
a
b
-
+
0
Różnica potencjałów V [V]
Prąd fotoelektryczny I w zależności od różnicy
potencjałów V. Krzywą b otrzymano przy mniejszym
natężeniu światła niż w przypadku krzywej a. Energia
kwantów jednakowa.
Jeżeli pole przyspiesza elektrony, wówczas obserwujemy
najpierw wzrost prądu, a następnie jego nasycenie
ograniczone zdolnością emisyjną katody.
h
V
I
Układ do
badania
fotoprądu I w
funkcji różnicy
potencjałów V
Wyjaśnienie własności zjawiska fotoelektrycznego jest
możliwe na podstawie kwantowej teorii światła. Zgodnie
z nią energia fotonu padającego na powierzchnię ciała
stałego zostaje pochłonięta przez elektron.
Część tej energii zostaje zużyta na oderwanie się od
elektronu od powierzchni, pozostałą część elektron
zachowuje w postaci energii kinetycznej. Stosując zasadę
zachowania energii możemy napisać:
h =  + Ekmax
Energia
kwantu
Praca
wyjścia
Energia
kinetyczna
(47)
równanie Einsteina
dla zjawiska
fotoelektrycznego.
Wpływ częstotliwości światła na przebieg zjawiska
fotoelektrycznego wyraża się zależnością napięcia
hamującego Vh od częstotliwości światła.
Istnieje pewna częstotliwość progowa 0 poniżej
której zjawisko fotoelektryczne nie zachodzi.
Częstotliwości progowej 0 odpowiada Ekmax = 0.
Zatem
h 0 = 
Energia
kwantu
(48)
Praca
wyjścia
W przypadku (48) foton ma tylko tyle energii, ile
potrzeba do wyjścia elektronu na zewnątrz z zerową
energią kinetyczną. Jeżeli h > , to wybite elektrony
mają energię kinetyczną, która pozwala im dotrzeć do
anody, a jeżeli ta energia jest wystarczająca, mogą
pokonać potencjał hamujący.
Odkrycie zjawiska fotoelektrycznego pozwoliło
na zbudowanie fotokomórki.
Albert Einstein (1879 – 1947)
Albert Einstein – jeden z największych fizyków-teoretyków
XX wieku, twórca ogólnej teorii względnościi, współtwórca
korpuskularno-falowej teorii światła, odkrywca emisji
wymuszonej. Laureat nagrody Nobla za wyjaśnienie efektu
fotoelektrycznego. Opublikował ponad 450 prac, w tym ponad
300 naukowych. Wniósł też swój wkład do rozwoju filozofii
nauki.
Zjawisko Comptona
Zjawisko Comptona polega na zderzeniu kwantu
promieniowania z elektronem słabo związanym z atomem.
Elektron taki traktujemy jako swobodną cząstkę, a samo
oddziaływanie kwantu z elektronem
traktujemy jako
zderzenie sprężyste. Zderzenie to musi podlegać prawu
zachowania energii i prawu zachowania pędu. Przed
zderzeniem elektron ma tylko energię spoczynkową m0c2, a
kwant enegię h0 i pęd pf0 równy
h
c
(49)
Po zderzeniu foton zostaje odrzucony w bok, tworząc kąt 
z pierwotnym swoim kierunkiem, natomiast elektron
uzyskuje pęd pe = mv i porusza się pod kątem .
Wektorowy wykres prawa zachowania pędu
w zjawisku Comptona
AB2 = OB2 + OA2 - 2OB • OAcos
(50)
A
pf
pf0


O
B
pe
Zapisujemy prawo zachowania energii i prawo
zachowania pędu dla zderzenia comptonowskiego.
h 0  m0c  h  m c



h 0 h

 mv
c
c
2
2
(51) Prawo zachowania energii
(52)
Prawo zachowania pędu
Na podstawie związków między bokami trójkąta OAB
można napisać:
h 0 h
2h
m v  2  2  2  0cos
c
c
c
2
2
2
2
2
2 2
(53)
lub
m v c  h  0  h  0  2h 0cos
2 2 2
2
2
2
2
2
(54)
Z równania (51) znajdujemy
mc2  h  0    m0c 2
(55)
skąd
m c  h 0   h   2h2 0
2 4
2
2
(56)
Odejmując od tego związku wyrażenie (53) znajdujemy
2


v
2 4
m c 1  2   m2c 4  2h 2 0 1  cos   2hm0c 2  0  
 c 
ale
(57)
2


v
2
2
m 1  2   m0
 c 
(58)
Wobec tego znajdujemy
h
c 0   
 0 1  cos 
m0 c
(59)
a następnie
c c
h
1  cos  
 
  0 m0c
c
0
c

 o
(61)

(62)
(60)
Wykorzystujemy związki
między prędkością c,
długością fali -  i
częstotliwością -  ,
indeks „0” oznacza
wartości przed zderzeniem
Wobec tego mamy wzór na zmianę długości fali w
zjawisku Comptona.
h
1  cos 
  0 
m0 c
 
h
1  cos   h sin 2 θ
m0 c
m0 c
2
Zwykle oznaczamy:
(63)
lub
(64)

h
 0.0242  10 10 m
m0 c
W zjawisku Comptona obserwujemy fotony rozproszone
pod różnymi kątami. Zmiana długości fali, a co za tym
idzie zmiana energii fotonu zależy od kąta rozproszenia.
Od kąta zależy też energia elektronów, które brały udział
w zderzeniu.
(65)
Ilustracja zjawiska Comtona

e-
’
Ilustracja wewnętrznego zjawiska
fotoelektrycznego

e-
Ilustracja zjawiska tworzenia się
par elektron - pozyton

e-
e+
Widmo kobaltu
60Co
Spektrometr scyntylacyjny
160
Liczba impulsow.
1.17 MeV
Zjawisko
Comptona
140
120
h > 2m0c2
1.33 MeV
100
80
60
Zjawisko
fotoelektryczne
40
20
0
0
100
200
Numer kanalu. Energia.
300
Widmo cezu
137Cs
Spektrometr scyntylacyjny
0.66 MeV
1200
Zjawisko
Comptona
Liczba impulsow.
1000
800
600
Zjawisko
fotoelektryczne
400
200
0
0
100
Numer kanalu. Energia.
h < 2m0c2
200