Krystyna Wosińska
Ewolucja Wszechświata
Wykład 3
1905 – Szczególna Teoria Względności:
•Istotny jest tylko ruch względny
•Skoro nie można stwierdzić, że ktoś się
porusza w przestrzeni, to pojęcie eteru
zbędne
•Prawa fizyki są jednakowe w każdym
układzie inercjalnym, w szczególności
prędkość światła jest stała
Ogólna Teoria Względności (1915):
G = 8T
geometria
Albert Einstein
1879 - 1955
materia
Ogólna Teoria Względności
Równoważność siły grawitacji i siły
bezwładności w układzie nieinercjalnym
•Pole grawitacyjne równoważne zakrzywieniu
czasoprzestrzeni
Przestrzeń i czas dotąd uważane za pasywną
scenę zdarzeń w istocie tworzą czasoprzestrzeń,
która jest dynamicznym uczestnikiem wszystkich
procesów.
Geometria Wszechświata
•Geometria płaska
model: dwuwymiarowa
płaszczyzna
Suma kątów w trójkącie
równa jest 1800
Linie równoległe nie
przecinają się
Geometria Wszechświata
•Geometria sferyczna
model: powierzchnia kuli krzywizna dodatnia
Suma kątów w trójkącie
równa jest większa niż 1800
Linie równoległe przecinają
się (przykład:południki)
Geometria Wszechświata
•Geometria hiperboliczna
model: powierzchnia siodłowakrzywizna ujemna
Suma kątów w trójkącie jest
mniejsza niż 1800
Linie równoległe rozchodzą się
Dr. Stanisław Bajtlik demonstruje powierzchnię o krzywiźnie ujemnej
... i dodatniej
Zakrzywienie czasoprzestrzeni oznacza, że najkrótszą linią
łącząca dwa punkty jest linia krzywa – światło w pobliżu dużej
masy nie porusza się po prostej!
Doświadczalne potwierdzenie Ogólnej Teorii Względności:
W 1919 r. zaobserwowano w czasie zaćmienia Słońca ugięcie
promieni świetlnych biegnących od odległej gwiazdy.
Pozorne położenie gwiazdy
Gwiazda
Słońce
Obserwator
Geometria Wszechświata
k<0
k=0
k>0
Wielkość k opisuje krzywiznę
Wszechświata
Krzywizna
Geometria
Suma
kątów w
trójkącie
Los Wszechświata
k>0
sferyczna
> 1800
Wielki Kolaps
k=0
płaska
= 1800
Wieczna ekspansja
k<0
hiperboliczna
< 1800
Wieczna ekspansja
Krzywizna zależy od gęstości Wszechświata
Gęstość krytyczna k – odpowiada wartości k = 0
8G k
H
3
2
3H 2
k
8G
Równanie Friedmana można przekształcić do postaci:
2
3kc
k
8Ga 2
Jeśli > k , to k > 0,
Jeśli < k , to k < 0,
= /k
- parametr gęstości
Miara płaskości Wszechświata:
k
3kc 2
1
8Ga 2
Gdy dominuje promieniowanie:
1
4
a
a2 t
Wartość 1 rośnie w czasie
Wszechświat z czasem robi się coraz mniej płaski.
= /k
- ten parametr wyznacza przyszłość Wszechświata
<1
=1
>1
Jeśli wyznaczymy , odkryjemy przyszłość Wszechświata
Geometria Wszechświata
Czy nasze istnienie byłoby możliwe we Wszechświecie o
dowolnej wartości ?
Zasada antropiczna
Przez tysiące lat ludzie wierzyli, że Wszechświat jest statyczny.
Einstein dodał do równania stałą kosmologiczną , aby „ratować”
płaski i statyczny Wszechświat.
2
8
G
kc
2
H
2
3
a
3
- reprezentuje siłę odpychającą, równoważącą przyciąganie
grawitacyjne – dzięki niej pojawia się rozwiązanie równania opisujące
statyczny Wszechświat.
W 1922 r. Aleksander Friedman znalazł wszystkie rozwiązania
równania i wykazał, że nawet dodanie stałej kosmologicznej nie
zapewni stałości Wszechświata.
Einstein nazwał dodanie stałej kosmologicznej swoją największą
pomyłką, jednak obecnie wcale nie jest oczywiste, że wynosi ona zero!
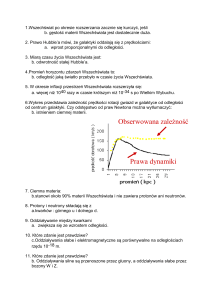
Ekspansja Wszechświata przyspiesza!
Supernowe znajdujące się w
odległości 3/4 drogi od krańca
Wszechświata pomogły odkryć,
że Wszechświat rozszerzał się
w różnym tempie podczas
swojej historii.
Poznamy dzieje Wszechświata, jeśli wyznaczymy trzy
parametry:
k
2
3 H
v
H
r
Pomiar stałej Hubble’a
Supernowe typu 1A stanowią doskonałe obiekty do pomiaru
odległości galaktyk – „świece standardowe”
Znamy dokładnie ich
jasność absolutną.
Jasność obserwowana
wyznacza odległość.
Prędkość ucieczki
galaktyk wyznaczona z
obserwowanego
przesunięcia linii
widmowych ku czerwieni.
Obecna wartość stałej Hubble’a:
H 71
4
km
3 ( s MPc)
Stała Hubble’a
Pomiar gęstości materii Wszechświata
Od gęstości zależy krzywizna Wszechświata
•Pomiar promieniowania świecących gwiazd i materii
międzygwiazdowej –materia świetlista
lum 0,005
Ωlum ~ 0.005
Pomiar gęstości materii Wszechświata
Od gęstości zależy krzywizna Wszechświata
•Pomiar zawartości lekkich pierwiastków powstałych w pierwszych 3
minutach po Wielkim Wybuchu - materia barionowa
b 0,04
•Pomiar oddziaływań grawitacyjnych – rotacja galaktyk - materia
grawitacyjna (ciemna materia)
dm 0,3
Wszechświat jest płaski!
Wynik badania promieniowania reliktowego (2003):
tot 1,02 0,02
Czy płaski Wszechświat
musi być nieskończony?
Karl Schwarzschild (1873 – 1916),
W 1900 pisał:
Wyobraźmy sobie, że w wyniku niezwykle wielkiego astronomicznego
przeglądu, okazałoby się, że cały Wszechświat jest wypełniony
identycznymi kopiami Drogi Mlecznej, że nieskończona przestrzeń może
być podzielona na komórki, z których każda zawiera identyczną kopię
naszej Drogi Mlecznej. Czy upieralibyśmy się przy założeniu, że istnieje
nieskończenie wiele identycznych kopii tego samego świata ? Czy nie
byłoby znacznie rozsądniej przyjąć, że te powtórzenia są iluzją, że w
rzeczywistości przestrzeń na szczególne własności spójności, takie, że
jeśli opuścimy daną komórkę przez jedną ścianę, to natychmiast
wejdziemy do niej przez ścianę przeciwną.
S. Bajtlik, Zjazd Fizyków 2005
S. Bajtlik, Zjazd Fizyków 2005
S. Bajtlik, Zjazd Fizyków 2005
S. Bajtlik, Zjazd Fizyków 2005
Dodecahedron – hipotetyczny
model Wszechświata
S. Bajtlik, Zjazd Fizyków 2005
S. Bajtlik, Zjazd Fizyków 2005
Teoria inflacji
Problemy, które trzeba wyjaśnić:
• Problem horyzontu
• Problem monopoli magnetycznych
• Problem płaskości Wszechświata
Problem horyzontu
Niezależnie od jakości teleskopów, nie możemy obserwować dowolnie
odległych obiektów. Największa odległość, w której światło zdążyło
dotrzeć do obserwatora w czasie istnienia Wszechświata wynosi :
R T c
Gdzie: T – wiek Wszechświata, c – prędkość światła
?
?
13,7 mld lat świetlnych
Horyzont można też zdefiniować
podstawiając do prawa Hubble’a
maksymalną prędkość ucieczki
galaktyk równą prędkości światła:
3·1027 cm
?
1
c H R R c T c
H
Problem horyzontu
Obserwujemy we wszystkich kierunkach wysoką jednorodność
Wszechświata, zarówno w skali wielkoskalowej (galaktyki,
gromady galaktyk), jak i promieniowania mikrofalowego, którego
natężenie i temperatura są identyczne we wszystkich kierunkach z
dokładnością do 1/10000.
A
Nasza galaktyka
B
Punkty A i B nie mogły ze sobą
oddziaływać od początku
istnienia Wszechświata, więc
skąd ta jednorodność...?
Problem horyzontu
T = 3·1028 K
T = 3K
Ekspansja o
czynnik 1028
Obecny horyzont
zdarzeń
Horyzont zdarzeń
3·10-25 cm
Wiek = 10-35 s
Wiek = 1017 s
W wieku 10-35 s Wszechświat składał się z ogromnej liczby niezależnych,
rozdzielonych obszarów?? Sprzeczność z obserwowaną jednorodnością!
Problem monopoli magnetycznych
Gdy Wszechświat miał 10-35 s i temperaturę 3·1028 K występowała
unifikacja trzech oddziaływań: silnego, słabego i elektromagnetycznego.
Teorie opisujące Wszechświat w tych warunkach przewidują powstanie
ogromnej liczby monopoli magnetycznych – cząstek o masach 1016 razy
większych niż masa protonu. Z obliczeń wynika, że monopoli byłoby teraz
tysiące razy więcej niż protonów czy neutronów.
Monopol jest pozostałością po chaosie, jaki istniał we wczesnym
Wszechświecie. Ponieważ Wszechświat był podzielony na obszary nie
oddziaływujące ze sobą, niejednorodności nie mogły się wyrównać i
tworzyły się monopole.
Jednak monopole nie są obserwowane!
Problem płaskości Wszechświata
Względna gęstość materii we Wszechświecie:
k
> 1 Wszechświat zamknięty (rozszerzanie zakończy się i rozpocznie zmniejszanie
< 1 Wszechświat otwarty (rozszerzanie będzie trwać w nieskończoność)
Początkowa wartość było bardzo niestabilna i jakiekolwiek
odchylenie od wartości 1 szybko wzrosłoby w czasie.
Problem płaskości Wszechświata
Aby dzisiejsza mieściła się w żądanym przedziale,
początkowa jej wartość
musiała być równa jedności z
dokładnością większą niż 1 na 10-15.
Początkowy Wszechświat był bardzo płaski!
Warunki początkowe Wszechświata zostały dostrojone z
wielką precyzją, aby mógł powstać dzisiejszy świat. Małe
wahanie na początku ewolucji Wszechświata sprawiłoby,
że zapadłby się w krótkim czasie lub materia tak szybko
by się oddalała, że nie powstałyby gwiazdy i planety.
Skąd to wykalibrowanie warunków początkowych?
Wszechświat inflacyjny
Pierwsze 10-43 s – czas Plancka – brak teorii opisującej Wszechświat
w tym stanie.
Po upływie czasu Plancka Wszechświat o temperaturze 1014 GeV
podlegał Wielkiej Unifikacji Oddziaływań (oddziaływania silne, słabe i
elektromagnetyczne nie różniły się).
Wszechświat zawierał obszary „fałszywej próżni” wypełnione ogromną
energią (pola Higgsa).
„Fałszywa próżnia” to obszar o zadziwiających własnościach:
•jej gęstość nie zmienia się wraz z rozszerzaniem się
•wytwarza ona ujemne ciśnienie
Z ciśnieniem jako formą energii związana jest grawitacja.
Ujemne ciśnienie prowadzi do odpychającej siły grawitacyjnej –
odpowiada tej sytuacji niezerowa stała kosmologiczna .
Nastąpiła ekspansja!
Inflacyjna ekspansja
INFLACJA
at 0
Równanie na przyspieszenie:
a
4G
3p
2
a
3
c
p
c
3
2
Przyspieszenie ekspansji związane jest
z ujemnym ciśnieniem.
Wszechświat inflacyjny
Wzór kosmologiczny:
2
8
G
kc
2
H
2
3
R
3
gdzie:
r
H
r
Te człony maleją gwałtownie
podczas rozszerzania
r
3
r
2
Zostaje:
Rozwiązanie równania:
r
r ( t ) exp
t
3
Ekspansja wykładnicza!
r
3
Wszechświat inflacyjny
Wykładnicza ekspansja zakończyła się w chwili 10-34 s po
Wielkim Wybuchu.
Jak powiększył się w tym czasie Wszechświat?
r ( t ) exp
t exp H t )
3
Załóżmy, że inflacja zaczęła się w chwili T = H-1 = 10-36 s
rkon
expH t kon t pocz e 99 1043
rpocz
Wszechświat powiększył się w ułamku sekundy
do rozmiarów wielokrotnie przekraczających
wszystko co możemy obserwować!
Wszechświat inflacyjny
„Istnieją poważne racje, by sadzić, że proces odłączania się
silnych oddziaływań jądrowych istotnie wpływa na zmianę
kwantowego stanu, zwanego kwantową próżnią, co z kolei
powoduje gwałtowne, niejako nadprogramowe, rozdęcie i tak
już rozszerzającego się Wszechświata. Zjawisko to nazywa
się kosmiczną inflacją. W ciągu małego ułamka sekundy
rozmiary Wszechświata powiększają się 1050 razy!”
M. Heller
Wszechświat inflacyjny
Wszechświat inflacyjny
Inflacja zakończyła się przejściem fazowem – „fałszywa
próżnia” zamieniła się w próżnię prawdziwą wypełnioną
cząstkami. Towarzyszyło temu wyzwolenie ogromnej energii,
która ponownie „podgrzała” Wszechświat
Analogia:
Uwolniona energia
woda
lód
Podczas przejścia fazowego uwalnia się energia
Wszechświat inflacyjny
Po zakończeniu okresu inflacji Wszechświat rozszerzał się dalej
ze stałą kosmologiczną równą zeru.
Teorię inflacji zaproponował w 1981 roku Alan Guth teoretyk
fizyki cząstek elementarnych zajmujący się Teorią Wielkiej
Unifikacji.
Wszechświat inflacyjny
Rozwiązanie problemu jednorodności Wszechświata:
3·10-25 cm
Obserwowalny Wszechświat powstał z bardzo małego
jednorodnego obszaru.
Wszechświat inflacyjny
Rozwiązanie problemu monopoli:
Wszechświat w chwili, gdy podlegał Wielkiej Unifikacji
Oddziaływań, nie był podzielony na obszary nie
oddziaływujące ze sobą.
Monopole nie powstawały.
Wszechświat inflacyjny
Rozwiązanie problemu płaskości Wszechświata:
Z równania Friedmana dla Wszechświata inflacyjnego
można otrzymać związek:
4
( t ) 1 exp
t
3
Oznacza on, że szybko dąży do jedności
Obecny Wszechświat jest płaski!
Światy równoległe?
Teoria inflacji otwiera olbrzymie pole do spekulacji.
Jedna z hipotez (której nigdy nie sprawdzimy!) mówi, że nasz
Wszechświat jest jednym z wielu (może nieskończenie wielu)
wszechświatów zawartych w „metawszechświecie”.
Każdy z tych Wszechświatów powstał z subatomowego obszaru
przestrzeni i stał się większy niż nasz widzialny Wszechświat w czasie
krótszym od 10-30 s. Mogły one powstawać w różnych miejscach i
czasach.
Hipotezy tej nie możemy zweryfikować doświadczalnie, bo nasze
obserwacje nie mogą wyjść poza horyzont zdarzeń w naszym
Wszechświecie!
Inflacja - podsumowanie
Różne odmiany modeli inflacyjnych mają następujące cechy wspólne:
•Pusta przestrzeń, nie będąca prawdziwą próżnią kipi energią.
•Energia ta powoduje, że pęcherzyk przestrzeni rozszerza się z
fantastyczną prędkością w czasie pierwszych chwil istnienia
Wszechświata
•Pod koniec tej fazy rozszerzania, około 10-34 s od Wielkiego Wybuchu,
dochodzi do przejścia fazowego, które tworzy prawdziwą próżnię i
ogromną liczbę cząstek oraz bardzo silnie ogrzewa Wszechświat.
•Po zakończeniu inflacji Wszechświat (który kiedyś był subatomowym
pęcherzykiem przestrzeni) rozszerza się tak, jak przewiduje teoria
Wielkiego Wybuchu, która powstała przed modelem inflacyjnym