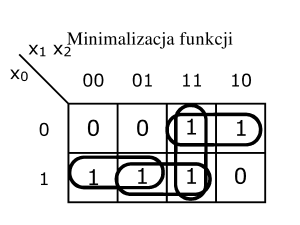
Wykład 7
Interpretacja Copenhagen’ska
Tradycyjna interpretacja procesu pomiaru wprowadzona była przez Bohra z
współautorami i wiadoma jest jako „interpretacja Copenhagenska” mechaniki kwantowej. Pna
może być podsumowana w kilku fundamentalnych założeniach.
Mechanika kwantowa opisuje indywidualne układy.
Mechanika kwantowa w podstawie swojej jest probabilistyczna, tj. ona nie może być
wyprowadzona z teorii deterministycznej (tak jak mechanika statystyczna).
Świat musi być podzielony na dwie części. Obiekt który jest badany musi być opisany
kwantowo-mechanicznie, a pozostała część, która zawiera też aparaturę pomiarową
musi być opisana klasycznie. Rozdzielenie między układem i aparaturą pomiarową
może być dokonane w dowolnym położeniu.
Proces obserwacyjny jest procesem nieodwracalnym.
Komplementarne własności nie mogą być zmierzone jednocześnie.
Interpretacja Copenhagenska ma przewagę nad innymi dzięki swoje prostocie i
wewnętrznej zgodzie. Możliwie ona nie jest przekonującej z estetycznego punktu widzenia,
ponieważ obejmuje dwa różne typy ewolucji: „normalną” unitarną ewolucję opisywaną
równaniem Schrödingera i nieunitarny proces pomiarowy. W ścisłym sensie, to oznacza, że
kwantowo-mechaniczne układy nie mogą posiadać realnych właściwości; rzeczywiście, one
wykazują „tylko” teorię o możliwych wynikach pomiarowych i ich prawdopodobieństwach.
Te niepełności mechaniki kwantowej stymulują wielu badaczy szukać lepszej
alternatywy, albo szukać sprawdzianów słuszności założeń mechaniki kwantowej.
Najszczególniejszy model, który próbuje zintegrować proces pomiarowy z ewolucją unitarna
na podstawie równania Schrödingera i obejść rozszczepienie wszechświata na część
kwantowo-mechaniczną i klasyczną, zaproponował John (znany też jako János albo Johann)
von Neumann.
Model von Neumanna
W tym modelu układ S oddziałuje za aparaturą A . Dla prostego dwupoziomego
układu stanami bazowymi są a i b - stany własne obserwabli układu O S . Pomiar musi
określić znajduje się układ w stanie a
czy w stanie b . Dla tego żeby użyć opisu
kwantowo-mechanicznego dla procesu pomiarowego, opiszmy aparaturę również jako układ
1
dwupoziomy. Własne stany zapiszemy jako a
i b
i one odpowiadają aparaturze
oznaczając odpowiednio, że układ znajduje się w stanie a
i b . Odpowiednia
obserwabla działająca na aparaturę zapiszemy jako O A .
Zgodnie z von Neumannem, proces pomiaru zawiera oddziaływanie układu z
pomiarową aparaturą za pomocą oddziaływania typu
H int OA B ,
(7.1)
gdzie O A - mierzalna obserwabla i B - zmienna aparatury pomiarowej. A zatem układ steruje
ruchem aparatury pomiarowej i w procesie idealizowanym wartości własne A mogą być
odczytywane „pomiarowym wskaźnikiem” (pointer variable) aparatury pomiarowej, którą
rozważamy jako klasyczną. Zwykle zakładamy, że obserwabla O A , którą próbujemy
zmierzyć komutuje z Hamiltonianem układu. W przypadku eksperymentu Sterna-Gerlacha
obserwabla O A jest z - składową operatora spinu S z , a pomiarowy wskaźnik mierzy
położenie z wzdłuż kierunku pola.
Przed procesem pomiarowym, całość (układ i aparatura) może być opisana jako stan
bez korelacji między układem i aparaturą. Dwie części można wtedy opisać indywidualnie za
pomocą stanów ca a cb b
(który nie jest wiadomy) i
oraz jako kombinację
w postaci iloczynu stanów
ca a cb b .
(7.2)
Oddziaływanie między układem i aparaturą musi być takim, żeby ono doprowadziło do
ewolucji
a a a
(7.3)
b b b .
(7.4)
i
Taka ewolucja jest liniową i stan superpozycyjny ewoluuje jak
c
a
a cb b ca a a cb b b .
(7.5)
Jest oczywistym, że kombinowany układ (składający się z układu i aparatury) pozostaje wciąż
w stanie superpozycyjnym, ale teraz dwie części stają się splątane. Model von Neumanna nie
generuje redukcji funkcji falowej, tak jak tego wymaga postulat rzutowy. To jest skutkiem
2
oczywiście unitarnej ewolucji. Redukcja powstaje tylko wtedy, jeżeli załóżmy, że aparatura
jest klasycznym układem, gdzie redukcja musi zachodzić. A zatem redukcja składowej
funkcji falowej aparaturowej w (na przykład) a powoduje redukcję stanu układu w a .
Ponieważ redukcję funkcji falowej nie jest wytłumaczono, znów znajdujemy się
daleko od rozwiązania problemu. Zgodnie z rozumieniem von Neumanna, końcowa redukcja
zachodzi w głowie obserwatora. Chociaż rozumowanie to nie daje całkowitego rozwiązania
paradoksu związanego z pomiarem, ono ulepsza sytuację. Ponieważ aparatura jest bardzo
złożoną dla tego, żeby opisać ją kwantowo-mechanicznie, kolaps jej funkcji falowej jest
bardzo szybki. Dalej, ponieważ to nie włącza bezpośrednie układ, niektóre sprzeczności
można zaakceptować. Ale wszystko jedno, główna teza pozostaje w modelu von Neumanna
nie rozwiązaną (zresztą we wszystkich innych podejściach też): z opisu kwantowomechanicznego otrzymujemy tylko prawdopodobieństwa, tj. nie możemy przepowiedzieć
wynik indywidualnych pomiarów.
Bramki kwantowe
Informacja jest zmagazynowana w zbiorze kubitów (rejestrze kwantowym) i musimy
być w stanie manipulować tymi kubitami. To oznacza, że musimy być w stanie zmienić stan
kubitu albo bezwarunkowo (na przykład, przeprowadzić kubit w stan początkowy, albo
zapisać informację zawartą w kubicie), albo warunkowo, czyli w zależności od poprzedniego
stanu tego samego kubitu (na przykład, operacja NOT) albo stanu innego kubitu (na przykład
kontrolne operacje NOT albo CNOT). Te zadania można wykonać za pomocą bramek
kwantowych. Oczywiście możemy wyobrazić sobie jeszcze więcej skomplikowane bramki,
które zmieniają stan jednego (albo kilku) kubitów w zależności od stanów dowolnej liczby
innych kubitów. Na szczęście wszystkie możliwe operacje można sprowadzić do
skończonego zbioru uniwersalnych bramek kwantowych. Z tych bramek możemy
skonstruować specjalne algorytmy dla procesów informatyki kwantowej. Okazuje się, że dla
skonstruowania uniwersalnych bramek kwantowych wystarczy niewielka liczba bramek jedno
albo dwukubitowych. W przypadku informatyki klasycznej żeby osiągnąć uniwersalność
musimy wykorzystywać trójbitowe operacje. A więc bramki kwantowe są „mocniejsze” niż
bramki klasyczne.
Rotacje dookoła osi współrzędnych
Wszystkie operatory w przestrzeni Hilberta jednego kubitu możemy przedstawić jako
kombinację czterech fundamentalnych operatorów 1, X , Y i Z (macierzy Pauli’jego).
3
Każdej unitarnej macierzy 2 2 odpowiada jedno - kubitowa bramka kwantowa.
Zwróćmy uwagę, że operatory X , Y i Z mają wartości własne 1 , a zatem są unitarne. To
jest oczywistym dla czego X często nazywają w języku informatyki kwantowej „bramką
NOT”; bramka Z generuje przesunięcie fazowe o między dwoma stanami bazowymi, a
Y iXZ jest kombinacją tych dwóch bramek. Dość łatwa jest generacja dowolnego
przesunięcia fazowego (nie tylko o ) między dwoma stanami. Zauważmy, że bramka
e i
exp iZ
0
0
,
e i
(7.6)
generuje względną fazę 2 . Ważnymi specjalnymi przypadkami tej bramki są
exp i
0
0
1
8
,
T 0 exp i exp i
8
0
exp i
4
8
(7.7)
(bramka / 8 ) i
1 0
,
S T 2
0 i
(7.8)
(często nazywana prosto bramką fazową). Zwróćmy uwagę, że S 2 Z .
Można wygenerować też NOT bramkę. Biorąc pod uwagę, że X 2 1 mamy
cos
exp iX 1 cos iX sin
i sin
i sin
,
cos
(7.9)
która interpoluje jak jedynkę, tak i NOT bramki dla 0 i / 2 odpowiednio. Dla / 4
otrzymujemy bramkę „pierwiastek kwadratowy z NOT”.
Ogólne rotacje
Z ogólnej teorii kwantowo-mechanicznej momentu pędu wiemy, że exp iq S (dla
dowolnego wektora q ) ma właściwości operatora rotacji. Rozważmy operator n S dla
dowolnego jednostkowego wektora n . Korzystając z algebraicznych własności spinowych
macierzy łatwo udowodnić, że kwadrat n S jest prosto proporcjonalny do jednostkowego
operatora
4
2
2
2
n S n x X n y Y n z Z 1 ,
(7.10)
a zatem
2
2
2
R exp i n S 1 cos i n S sin .
n
(7.11)
Zauważmy, że
Rn Rn Rn1 .
(7.12)
Ten operator komutuje ze spinową składową n S , a zatem nie zmienia tej specyficznej
komponenty. Można pokazać, że unitarne przekształcenie Rn odpowiada rotacji o kąt 2
dookoła osi n . Podkreślimy, że ten obrót możemy interpretować na kilka sposobów.
Oczekiwana wartość S wektora spinowego pod wpływem Rn przyłożonego do stanu
kubitu rotuje o kąt 2 . Alternatywnie ale ekwiwalentnie możemy uważać, że wektor spinowy
S rotuje przy działaniu na niego unitarnego przekształcenia Rn SRn . Zwróćmy uwagę,
że wektor polaryzacji P na sferze Blocha rotuje jak wektor S .
Pokażemy teraz jawnie, że Rn opisuje rotacje o 2 dla dowolnego n , ale tylko
dla n , który pokrywa się z jednostkowym wektorem wzdłuż osi z
e i
Rz exp iZ
0
0
.
e
i
(7.13)
Dla dowolnego stanu czystego , otrzymujemy
e i
R z ,
0
2
exp i
cos
i ( / 2 )cos( / 2 )
0 e
2
2
, 2 . (7.14)
i i ( / 2 )sin / 2
e e
exp i 2 sin
2
2
Zwróćmy uwagę, że obrót o 2 ( ) zmienia znak dowolnego jedno - kubitowego stanu,
jednak to nie jest słuszne dla oczekiwanych wartości fizycznych obserwabli w tym stanie
Rotacje kompozycyjne
Ponieważ unormowany czysty stan kubitu jest reprezentowany punktem na
powierzchni sfery Blocha, a dwa dowolne punkty na sferze są związane rotacją, to dowolny
unitarny jedno - kubitowy operator możemy zapisać w postaci
5
U e i Rn .
(7.15)
Często dogodniej jest wykorzystywać tylko rotacje dookoła osi współrzędnych zamiast rotacji
dookoła dowolnej osi n . To jest rzeczywiście możliwe; dla dowolnego unitarnego operatora
U jest słuszne przedstawienie
U e i Rz Ry Rz .
(7.16)
Możliwe też jest przedstawienie z zamianą z na x . Drugie przedstawienie, które będziemy
dalej stosować jest dość blisko związane z powyższym jedno - kubitowym Z Y
przedstawieniem. Niech
A R z R y ;
2
B R y Rz
;
2
2
C z Rz
,
2
(7.17)
gdzie , i określa (7.16). Zauważmy, że
ABC 1 .
(7.18)
Dalej relacje między macierzami Pauli’jego
XYX Y ;
XZX Z
(7.19)
mogą być wykorzystane dla tego, żeby pokazać, że
XBX R y R z
,
2 2
(7.20)
a zatem
e i AXBXC e i Rz Ry Rz U .
(7.21)
Wstawiając więc dwa operatory X (bramki NOT) można konwertować operator U w
operator unitarny.
Dwu- kubitowe bramki. Kontrolne bramki
Wszystkie języki programowania zawierają strukturę kontrolne typu: „wykonać
operację Y , jeżeli warunek X jest spełniony”. W kwantowej informatyce te struktury
realizują się za pomocą multi-kubitowych bramek, które mają jeden albo więcej kontrolnych
kubitów i kubitów celowych. Najprostszym przypadkiem jest dwu-bitowa (albo dwu kubitowa) operacja znana jako „kontrolny NOT” (CNOT), która jest określona następującą
tabelą prawdy, przedstawioną niżej. Kontrolny kubit pozostaje bez zmian, ale celowy kubit
6
zmienia się, jeżeli kontrolny kubit jest równy 1. (Dla uproszczenia piszemy 1 zamiast 1 ).
Kolumna „result” tabeli prawdy zawiera jak kontrolny, tak i celowy kubity. Zauważmy, że
wyjściowy celowy kubit jest równy „wyłączające albo- exclusive or” (XOR) między
kontrolnym i celowym kubitami. A zatem operacja CNOT nazywa się również „rewersyjną
XOR”, ponieważ odwracalność wykonuje się za pomocą zachowania wartości kontrolnego
kubitu, w przeciwieństwie do zwykłej (nieodwracalnej) XOR operacji klasycznego
komputera. Faktycznie rewersyjna XOR pokrywa się z jej odwróconą operacją. Symbolicznie
to zostaje osiągnięte następującym mapowaniem
x, x x, xXORy ,
(7.22)
i to może być wykorzystane do kopiowania bitu, ponieważ
x,0 x, x ,
(7.23)
Kombinacja trzech bramek CNOT (w drugiej z których role kontrolnego i celowego bitów są
odwrócone) wymienia (swaps) zawartość dwóch bitów, co można sprawdzić powtarzając
działania (7.22). A więc bramka CNOT może być wykorzystana dla kopiowania i wymiany
bitów. W oznaczeniu macierzowym w zwykłej bazie komputerowej
00 , 01 , 10 , 11 ,
bramka CNOT wygląda następująco
1
0
CNOT
0
0
0 0 0
1 0 0 1
0 0 1 0
0 1 0
0
X
(7.24)
wykorzystując oznaczenie 2 2 blokowej macierzy. Zamieniając X przez dowolny unitarny
jedno-kubitowy operator U , dochodzimy do kontrolowanej- U (CU) bramki.
Bramki kompozycyjne
Rolę kontrolnych i celowych kubitów mogą być przesunięte za pomocą przekształceń
(w indywidualnych kubitowych przestrzeniach Hilberta). Jeden z przykładów jest
przedstawiony na rys.7.1.
7
Tutaj kontrolny i celowy kubity mogą wymienić się swoimi rolami po zastosowaniu
bramki Hadamarda do każdego kubitu do i po działaniu operacji CNOT. To można sprawdzić
zapisując jawnie dwu - kubitową macierz transformacji Hadamarda H1 H 2 i wykonując
mnożenie macierzowe.
Rys.7.1. Nieokreśloność kontrolnego i celowego kubitów
Bramka CU może być zrealizowana za pomocą CNOT i jedno-kubitowej bramki. Idea
polega na zastosowaniu przedstawienia (7.21) i wykorzystaniu U e i AXBXC jeżeli kubit
kontrolny jest określony (set) i ABC 1 w przeciwnym przypadku. Na rys.7.2 obwód
przedstawia ten trik.
Zwykle mnożnik fazowy e i , tak samo jak dwie operacje NOT (= X ) są aktywne
tylko gdy kontrolny kubit jest określony.
Rys.7.2. Obwód dla kontrolnej U - bramki
Bramki CNOT i Hadamard mogą być wykorzystane, na przykład, do tworzenia
maksymalnie splątanych stanów z czterech dwu-kubitowych obliczeniowych stanów
bazowych a, b (gdzie a, b 0,1 ) jako
ab CNOT a, bH (a) a, b .
(7.25)
Jako przykład, rozważmy
H 0,0
1
2
0,0
1,0
8
00
1
2
0,0
1,1 ,
(7.26)
co daje jeden ze stanów Bella. Inne wartości a, b dają pozostałe człony bazy Bella.
W operacjach kontrolnych wyższego rzędu stosują się n kontrolne kubity i k celowe
kubity; ważny przykład jest bramka Toffoli (control-control-NOT albo C2NOT), albo ogólnie
C2U bramka dla niektórego dowolnego jednego kubitu U . Zwykle, C2U bramka może być
zbudowana ze CNOT i jedno-kubitowych bramek. Dla tego, żeby widzieć to, rozważmy
unitarny operator V , dla którego V 2 U (który zawsze istnieje) i zbudujemy obwód
pokazany na rys.7.3.
Rys.7.3. Obwód dla kontrol-kontrol-U bramki: V 2 U
Jeżeli nie jeden kontrolny kubit nie jest określony, nic nie zachodzi. Jeżeli jeden z
kontrolnych kubotów jest wprowadzony, V V 1 i jeden V działa na kubit celowy. Jeżeli
oba kontrolne kubity są wprowadzone, V nie powoduje wymiany, ale obaj V tak.
Interesującym jest fakt, ze z kwantowymi rewersyjnymi bramkami, bramka Toffoli może być
rozłożona na jedno- i dwu-kubitiwe bramki, co nie jest możliwe klasyczne. Bramka Toffoli
(tak jak inne bramki) mogą być zbudowane z bramki Hadamarda, fazowej bramki, CNOT i
bramki / 8 .
Uniwersalny zbór bramek
Ważne jest wiedzieć czy dowolny unitarny operator w interesującej nas przestrzeni
Hilberta może być przedstawiony w postaci sekwencji skończonej standardowych
elementarnych operatorów. Jeżeli to jest tak, czy możliwe jest zbudowanie uniwersalnego
kwantowego komputera, który może rozwiązywać dowolne zagadnienia, podobnie do
zwykłych klasycznych cyfrowych komputerów, które są (w zasadzie) zbudowane z bardzo
małej liczby uniwersalnych klasycznych bramek. Okazuje się, ze istnieje zbiór uniwersalny
bramek kwantowych, w tym sensie, ze dowolny unitarny operator może być przedstawiony z
dowolną dokładnością jako kombinacja tych bramek.
9
Jak już podkreślone wyżej, kolejne cztery bramki spełniają to:
Bramka CNOT,
Bramka / 8
0
1
exp i 1 Z ,
T
8
0 exp i / 4
(7.27)
Bramka fazowa
1 0
S T 2
0 i
(7.28)
(zauważmy, że S 2 Z ) i
Bramka Hadamarda
H
1
2
X Z
1 1 1
.
2 1 1
(7.29)
Można wykazać, że ten zbiór czterech bramek jest uniwersalny w procesie trzech
stopniowym.
1. Dowolny unitarny operator może być przedstawiony (dokładnie) jako iloczyn
unitarnych operatorów zawierających tylko dwa komputerowych bazowych stany :
„dwu-poziome bramki są uniwersalne”
2. Dowolny unitarny operator może być przedstawiony (dokładnie) za pomocą jednokubitowej i CNOT- bramek: „Jedno-kubitowa i CNOT bramki są uniwersalne”.
3. Jedno-kubitowe operacje mogą być aproksymowane z dowolną dokładnością
wykorzystując bramki Hadamarda, fazową i / 8 .
Unitarne operacje
Zaczniemy od kroku 1: Dwu-poziome bramki są uniwersalne; co oznacza, że dowolna
macierz d d unitarna U może być zapisana jako iloczyn (nie więcej niż) d (d 1) / 2 dwupoziomych unitarnych macierzy (macierzy unitarne, które działają nietrywialnie tylko nie
więcej niż na dwie składowe wektora). To można udowodnić następująco. Rozważmy lewy
kąt macierzy unitarnej
a d
U b c .
. .
10
(7.30)
Macierz unitarna 2 2
U1
a*
2
2 b
a b
b*
a
1
(7.31)
eliminuje drugi element w pierwszej kolumnie U
a a/
U 1 .
b 0
(7.32)
(Wykorzystaliśmy, bez dodatkowych oznaczeń, U 1 dopełnioną jednostkową macierzą
rozmiarem (d 2) (d 2) tak aby iloczyn U1U miał sens). Dalej mogą być wykorzystane
unitarne macierzy 2 2 dla eliminacji kolejnych elementów w pierwszej kolumnie U
1 0
U d 1U d 2 U 1U 0 c /
0
0
.
(niezerowe )
(7.33)
Zwróćmy uwagę, że na początku pierwsza kolumna miała normę jedynkę, ponieważ
U jest unitarną. Wykorzystujemy tylko unitarne operacje (tj. zachowujące normę), tak że
końcowy wynik pozostaje jednostkowym wektorem, który ma niezerową składową, która
musi być 1. (Faza musi być wyeliminowana.) Dzięki iloczynu unitarnych macierzy wszystkie
elementy w pierwszej lewej kolumnie muszą też znikać. Proces eliminacji może być
kontynuowany dla drugiej kolumny i ostatecznie mamy
U k U k 1 U 1U 1
d (d 1)
d 1 d 2 1 ,
k
2
(7.34)
skąd
U U 1U 2 U k ,
(7.35)
co udowadnia możliwość przedstawienia dowolnej bramki U przez bramki dwu-poziomowe.
11