Bronisław TOMCZUK, Dariusz KOTERAS
Politechnika Opolska, Katedra Elektrotechniki Przemysłowej
Analiza pola magnetycznego modułowych transformatorów
amorficznych przy wymuszeniu nieskompensowanym
magnetycznie
Streszczenie. W pracy przedstawiono wyniki trójwymiarowych analiz pola magnetycznego w transformatorach amorficznych budowy modułowej
przy zasilaniu uzwojeń prądem jednakofazowym. Do obliczeń zastosowano Metodę Elementów Skończonych. Obliczenia indukcji magnetycznej i
strumieni zweryfikowano pomiarowo i otrzymano dobrą zgodność wyników.
Abstract. The results of 3D magnetic field analysis for modular amorphous transformers under supplying of the windings with uniphase current have
been presented in this work. Finite Element Method has been employed. The magnetic flux density and fluxes calculations have been verified by
measurements and a good agreement of the results was obtained. (Magnetic field analysis in modular amorphous transformers under non
compensated magnetic excitation).
Słowa kluczowe: trójwymiarowa analiza polowa, modułowe transformatory amorficzne, zasilanie jednakofazowe.
Keywords: 3D field analysis, modular amorphous transformer, uniphase supplying.
Wprowadzenie
Wraz z rozwojem różnych dziedzin przemysłu takich jak
energoelektronika, technika komputerowa, stawiane są
nowe wymagania dotyczące współpracy transformatorów z
siecią zasilającą. W ostatnich latach nastąpił znaczny
postęp
w
produkcji
sterowanych
elementów
półprzewodnikowych, takich jak tranzystory i tyrystory.
Zaawansowana technika mikroprocesorowa umożliwia
skomplikowane sterowanie różnego typu przekształtników.
W wielu przypadkach warunki ich pracy uniemożliwiają
bezpośrednie włączenie do sieci i wymagają zastosowania
układów pośredniczących zawierających transformatory lub
autotransformatory [1]. W układach przekształtnikowych
transformatory mogą być umieszczone pomiędzy siecią a
przekształtnikiem lub na wyjściu falownika [1]. W drugim z
w/w przypadków transformatory lub dławiki pracują przy
podwyższonej częstotliwości i silnie odkształconym
napięciu, co powoduje znaczne zwiększenie strat. Napięcia
i prądy o częstotliwościach będących wielokrotnością 3n
(gdzie n∈N) częstotliwości sieciowej są nazywane prądami i
napięciami jednakofazowymi [2]. Strumienie magnetyczne
wytworzone przez tego rodzaju prądy i napięcia mają
zdecydowanie inny rozkład niż strumienie harmonicznych
niepodzielnych przez 3. Dlatego też ich określenie jest
konieczne. Najlepiej wykonać 3-wymiarową symulację pola
magnetycznego, która pozwala wyznaczyć miejsca
szczególnej koncentracji strat z prądów wirowych.
W połowie XX w. odkryto materiały amorficzne, które
charakteryzują się dobrymi własnościami magnetycznymi
takimi jak, niewielka wartość natężenia pola koercji ( około
2,5 [A/m]) oraz stosunkowo wysoka wartość indukcji
nasycenia (1,6 [T]) [3]. Dzięki temu znajdują coraz szersze
zastosowanie do budowy rdzeni magnetycznych. Ich
główną zaletą jest kilkakrotnie mniejsza stratność w
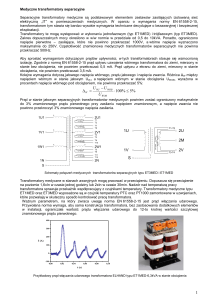
odniesieniu do blach krzemowych (M150-35S) [4]. Na
rysunku 1 przedstawiono stratności wybranego stopu
amorficznego na bazie żelaza (Fe) dla różnych wartości
częstotliwości sygnału zasilającego [5]. Chociaż straty te są
kilkakrotnie mniejsze od strat w tradycyjnie stosowanych
materiałach miękkich magnetycznie to widać, że wzrastają
one szybciej niż liniowo wraz ze wzrostem „f”
Znaczne odkształcenie strumieni magnetycznych
występuje w transformatorach współpracujących z
przekształtnikami, szczególnie tych umieszczonych na
wyjściu
falowników.
W
transformatorach
przekształtnikowych strumienie jarzmowe posiadają w istotnej
części częstotliwość 3-krotnie większą od częstotliwości
96
przemysłowej [6]. Ze względu na nieliniowość materiałów
ferromagnetycznych, sinusoidalny przebieg (w funkcji
czasu) strumieni magnetycznych występuje gdy prąd
magnesujący zawiera wszystkie wyższe harmoniczne. W
pewnych układach połączeń transformatorów, np. gdy
uzwojenie pierwotne skojarzone jest w gwiazdę bez
przewodu zerowego, prąd strony pierwotnej nie zawiera
trzeciej harmonicznej co powoduje odkształcenie strumieni
magnetycznych. Trzecie harmoniczne (będące ze sobą w
fazie) strumieni magnetycznych nazywane są strumieniami
jednakofazowymi [2]. W przypadku, gdy wychodzą one z
jarzm
transformatora
nazywane
są
strumieniami
jarzmowymi. Strumienie te zamykają się poprzez obszar
rozproszeniowy, elementy konstrukcyjne oraz, w przypadku
transformatorów olejowych, przez kadź. Powoduje to
lokalne nagrzewanie się tych elementów i powstawanie
dodatkowych strat mocy. Straty te znacznie wzrastają dla
strumieni jednakofazowych o częstotliwości 3nf, (gdzie
n∈N, a f jest częstotliwością sieci [6]).
Rys.1. Stratności wybranego stopu amorficznego na bazie Fe dla
różnych częstotliwości zasilania [5]
Powstanie strumieni jednakofazowych może wynikać
również z niesymetrii zasilania lub obciążenia. Niesymetria
ta, a szczególnie obciążenia, często występuje w sieci
energetycznej. Do analizy obwodowej takich przypadków
wykorzystuje się metodę składowych symetrycznych, która
pozwala na wyodrębnienie składowych: zgodnej, przeciwnej
i zerowej prądów i napięć [7]. Prądy składowej zerowej nie
występują w przypadku skojarzenia transformatora w
gwiazdę lub zygzak bez przewodu zerowego. Powoduje to
powstanie nieskompensowanego strumienia jednakofazowego. Należy dodać, że takie układy połączeń są
często stosowane w praktyce zarówno w układach połączeń uzwojeń transformatorów małej jak i dużej mocy [7].
PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 85 NR 3/2009
Analizowane obiekty
Analizę polową przeprowadzono dla dwóch typów 3fazowych
transformatorów
amorficznych
budowy
modułowej. Pierwszy z nich to transformator amorficzny z
rdzeniem symetrycznym (TSM -transformator symetryczny
magnetycznie). Natomiast drugi obiekt to transformator z
rdzeniem niesymetrycznym (TNM – transformator
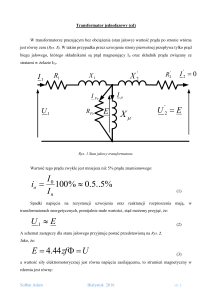
niesymetryczny magnetycznie). Rysunek 2 przedstawia
szkic aksonometryczny transformatora TSM, a na rysunku 3
zamieszczono szkic transformatora TNM. Dodatkowo na
w/w rysunkach podano przyjęte układy współrzędnych
kartezjańskich oraz podstawowe wymiary rdzeni. Ponieważ
układy uzwojeń były jednakowe dla obu obiektów, wymiary
układu uzwojeń podano jedynie na rysunku 3.
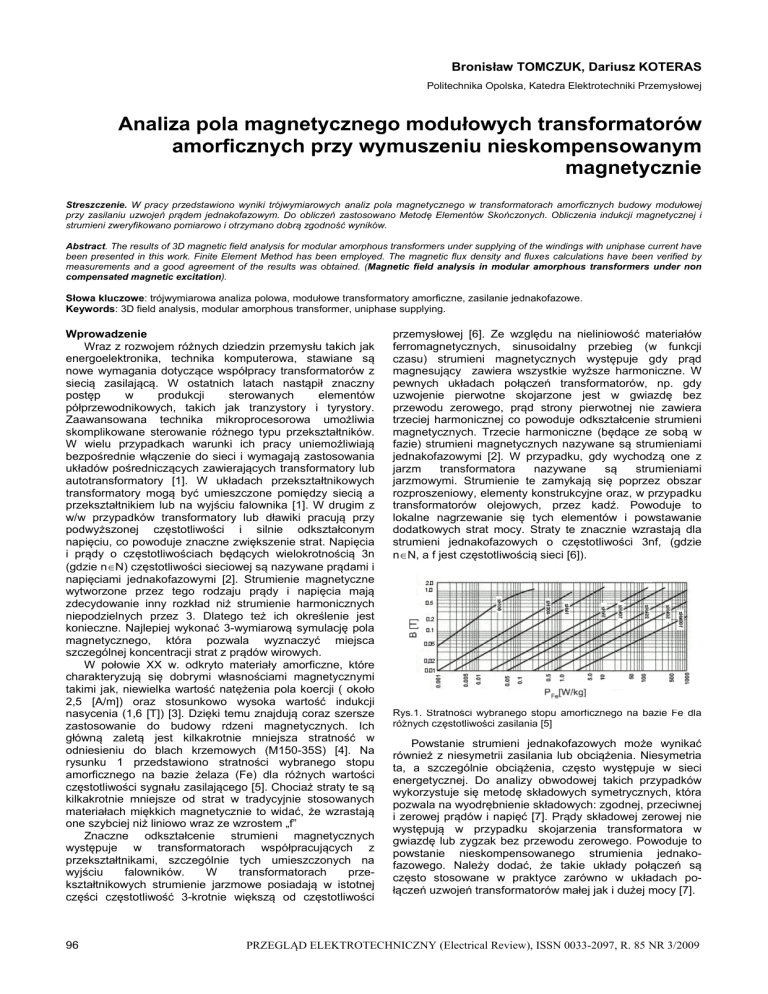
poszczególnych elementów rdzeni wraz z układem
uzwojeń) wykonano konstrukcje transformatorów 1fazowych z jarzmami: zwijanymi toroidalnym i podwójnie
podkowiastym [5]. Transformatory w tej konfiguracji
przedstawiono na rysunkach 4a i 4b.
Rys. 4. Konstrukcje 1-fazowe badanych transformatorów
a) na bazie transformatora TSM, b) na bazie transformatora TNM
Rys.2. Główne wymiary transformatora z rdzeniem symetrycznym
magnetycznie (TSM)
Model obliczeniowy
W niniejszej pracy analizowano przede wszystkim
konstrukcjie 3-fazowe transformatorów budowy modułowej
z rdzeniem amorficznym. Dla 3-fazowego układu połączeń
Yy0 obliczono strumień jednakofazowy powstający w
przypadku 1-fazowego obciążenia strony wtórnej. W takim
przypadku składowe zerowe prądów strony wtórnej dla
wszystkich faz są równe. W przypadku modeli fizycznych
(rys. 2 i 3) wynosiły one kolejno Ia0= Ib0= Ic0=8,67 [A].
Natomiast dla konfiguracji 1-fazowych przyjęto do obliczeń
wartości prądów I=2,4 [A]. Zamodelowe wartości prądów
wynikały z trudności wymuszenia prądu I=8,67 [A] do
weryfikacji pomiarowej.
Do obliczeń polowych wykorzystano Metodę Elementów
Skończonych (MES) zaimplementowaną w komercyjnym
pakiecie Opera 3D. Algorytm obliczeniowy w/w pakietu
oparty jest na opisie równań Maxwella za pomocą dwóch
potencjałów skalarnych: całkowitego-ψ i zredukowanego-φ
[8]. Dlatego, też w obszarach w których nie występują prądy
wymuszające pole, obowiązuje następujące równanie
różniczkowe cząstkowe
(1)
∇ ⋅ (μ∇ψ ) = 0
gdzie: μ – przenikalność magnetyczna.
Natomiast w podobszarach zawierających gęstości
prądów (wymuszenia) rozwiązywane jest poniższe
równanie Poissona
(2)
Rys.3. Główne wymiary transformatora z rdzeniem niesymetrycznym
magnetycznie (TNM)
W celu weryfikacji pomiarowej analizy pola wykonano
modele fizyczne, o jednakowych parametrach (napięcia i
prądy) zasilania i obciążenia. Dane znamionowe
transformatora
TNM
wykonanego
w
Katedrze
Elektrotechniki Przemysłowej Politechniki Opolskiej podano
w tabeli 1.
Tabela 1. Dane znamionowe transforatora TNM
Moc
S=10 [kVA]
Napięcie
U1=380 [V]
U2=220 [V]
Prąd
I1=15,2 [A]
I1=26 [A]
Liczba zwojów
N1=191
N1=116
Wykorzystując
prostotę
i
transformatorów TSM i TNM
szybkość
(skręcenie
montażu
śrubami
(
)
G
∇ ⋅ (μ∇φ ) − ∇ ⋅ μH S = 0
G
Wartość H S wyznacza się z prawa Biota-Savarta i jest
to natężenie pola magnetycznego wytworzonego w
środowisku jednorodnym (powietrze) jedynie przez
wymuszenia prądowe.
Siatki elementów skończonych w analizowanych 3wymiarowych obszarach były tworzone z graniastosłupów.
Nieograniczoność pola dla analizowanych obiektów
wymagała modelowania warunków brzegowych na
granicach obszarów kilkakrotnie większych od wymiarów
zewnętrznych transformatorów. Ze względu na symetrię
transformatora TNM obszar obliczeniowy dotyczył jedynie
połowy strefy rozproszeniowej tego obiektu. Z uwagi na
spakietowanie rdzeni w obliczeniach polowych pominięto w
nich rozkłady prądów wirowych.
Wyniki obliczeń polowych
W wyniku obliczeń polowych otrzymano przestrzenne
rozkłady indukcji magnetycznej zarówno na zewnątrz jak i
wewnątrz rdzenia. Na rysunkach 5 i 6 przedstawiono
PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 85 NR 3/2009
97
rozkłady składowej BZ, w odległości 5 [mm] od powierzchni
żelaza, nad powierzchnią górną jarzm obu transformatorów.
W/w rysunki dotyczą strumieni jarzmowych wytworzonych
przez pole magnetyczne w przypadku jednakofazowych
prądów o wartości I=8,7 [A].
Z przedstawionych histogramów indukcji wynika, że
największe wartości indukcji w powietrzu występują w
okolicy zewnętrznych krawędzi jarzm. W transformatorze
TSM przedstawione rozkłady składowej BZ indukcji są
symetryczne względem osi OZ. Dla transformatora TMN
wartości BZ nad zewnętrznymi kolumnami są około
dwukrotnie większe niż nad kolumną środkową pomimo
jednakowych wartości prądów 3-harmonicznej we
wszystkich kolumnach.
Rys.8. Rozkład składowej BZ dla transformatora 1-fazowego z
jarzmem dwupodkowiastym
Rozkłady składowej BZ indukcji magnetycznej nad
powierzchnią górną w odległości 5 [mm] od rdzenia, dla
konfiguracji 1-fazowych przedstawiono na rysunkach 7 i 8.
Porównanie odpowiednich rysunków (5 i 7 oraz 6 i 8)
prowadzi do wniosku, że strumienie jednakofazowe
rozpływają się podobnie, co potwierdza podobieństwo
rozkładów indukcji. Tak więc, na rozkłady strumienia
jarzmowego ma wpływ jedynie konfiguracja rdzenia,
bowiem stumień zamyka się porzez powietrzną strefę
rozproszeniową.
Obliczono również strumienie magnetyczne w połowie
wysokości kolumn dla 3-fazowych transformatorów. Wyniki
obliczeń przedstawiono w tabeli 2.
Rys.5. Rozkład składowej BZ nad jarzmem transformatora TSM
Tabela 2. Obliczone wartości strumieni magnetycznych w [μWb]
TSM
TNM
Φa
Φb
Φc
Φa
Φb
Φc
ΣΦ
ΣΦ
381 380 380 1141 388 368 387 1143
W transformatorze TSM strumienie rozkładają się
równomiernie na wszystkie trzy kolumny. Z kolei w
transformatorze TNM strumienie kolumn zewnętrznych są
większe od strumienia kolumny środkowej, co świadczy o
prawidłowości obliczeń [7].
Rys.6. Rozkład składowej BZ nad jarzmem transformatora TNM
Rys.7. Rozkład składowej BZ dla transformatora 1-fazowego z
jarzmem toroidalnym
98
Weryfikacja pomiarowa wykonanych obliczeń
Przeprowadzone
obliczenia
polowe
zostały
zweryfikowane pomiarowo. Pomiary indukcji magnetycznej
wykonano teslomierzem hallotronowym typu 4048 firmy
Bell. Dla transformatora TSM linia pomiarowa przebiegała
wzdłuż promienia jarzma zawierającego oś symetrii
pomiędzy kolumnami. Z kolei dla drugiego obiektu (TNM)
linia pomiarowa była równoległa do osi OX i odległa od niej
o 2,5 [cm]. Porównane wartości indukcji dla układów 3fazowych przedstawiono na rysunkach 9 i 10. Z kolei dla
konfiguracji 1-fazowych rozkłady te przedstawiono
rysunkach 11 i 12.
Rys.9. Składowa BZ nad jarzmem transformatora TSM
PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 85 NR 3/2009
zmierzonymi wynoszą około 5 %. Różnice te wynikają z
pewnej niesymetrii modeli fizycznych.
Tabela 3. Zmierzone wartości strumieni magnetycznych w [μWb]
TSM
TNM
Φa
Φb
Φc
Φa
Φb
Φc
ΣΦ
ΣΦ
391 383 402 1176 415 386 403 1204
Rys.10. Składowa BZ nad jarzmem dla transformatora TNM
Rys.11. Składowa BZ nad jarzmem transformatora 1-fazowego z
jarzmem toroidalnym
Rys.12. Składowa BZ nad jarzmem transformatora 1-fazowego z
jarzmem dwupodkowiastym
Uzyskano dobrą zgodność obliczeń i pomiarów.
Największe różnice pomiędzy wartościami zmierzonymi i
obliczonymi wynoszą około 10 %. Wynikają one z
pominięcia w obliczeniach elementów konstrukcyjnych.
Ponadto przy niewielkich mierzonych wartościach indukcji
duży wpływ ma niedokładność pozycjonowania sondy
pomiarowej.
Zweryfikowano
również
obliczenia
strumieni
magnetycznych w kolumnach. Pomiary wykonano za
pomocą sond umieszczonych bezpośrednio na kolumnach.
Otrzymane wartości strumieni zamieszczono w tabeli 3.
Pomimo stosunkowo niewielkich wartości strumieni,
względne różnice pomiędzy wartościami obliczonymi i
Wnioski
Opracowanie nowych konstrukcji modułowych rdzeni
amorficznych wymaga wyznaczenia ich parametrów w
różnych stanach pracy, również w czasie ewentualnej
awarii. Analizowane zagadnienie może mieć znaczenie
praktyczne ze względu możliwość częstego występowania
warunków powodujących powstawanie tych strumieni
Chociaż wartości indukcji magnetycznej w powietrzu
przy wzbudzeniu jednakofazowym są w niniejszej pracy
małe to w przypadku zwarcia awaryjnego są dużo większe i
mogą decydować o dużych siłach elektrodynamicznych [9].
Rozkład pola rozproszenia strumienia jarzmowego nie
zmienia się znacząco w zależności od konfiguracji rdzeni
(np. rys. 6 i 8). Otrzymano dobrą zgodność obliczeń z
pomiarami.
Na podstawie przeprowadzonej analizy wykazano
przydatność MES do obliczeń nieograniczonych strumieni
jednakofazowych. Analizowane zagadnienie może mieć
znaczenie praktyczne ze względu na możliwość częstego
występowania warunków powodujących powstawanie tych
strumieni.
LITERATURA
[1] T u n i a H . i i n n i , Układy energoelektroniczne obliczanie,
modelowanie, projektowanie, WNT, Warszawa, (1982)
[2] T o m c z u k B . Trójwymiarowe modelowanie nieograniczonych
pól magnetycznego rozproszenia transformatorów i dławików z
zastosowaniem metod całkowych, Studia i Monografie, Zeszyty
naukowe WSI, (1994), nr 77
[3] S o i ń s k i M . , Materiały magnetyczne w technice, Centralny
Ośrodek Szkolenia i Wydawnictw SEP, Warszawa, (2001)
[4] T o m c z u k B . , K o t e r a s D . , Nowoczesne konstrukcje
transformatorów małej mocy o rdzeniach amorficznych,
Przegląd Elektrotechniczny, (2003), nr 12, 875-879
[5] T o m c z u k B . , Z a k r z e w s k i K . , K o t e r a s D . W a i n d o k
A . , Z i m o n J . , Badanie właściwości fizycznych i parametrów
energetycznych suchych transformatorów z rdzeniami
amorficznymi, Raport z realizacji pracy badawczej własnej, nr
4T10A 050 24, Opole, V, (2005)
[6] T u r o w s k i J . , Elektrodynamika techniczna, WNT, Warszawa,
Wydanie II zmienione, (1993)
[7] J e z i e r s k i E . , Transformatory, WNT, Warszawa, (1983)
[8] OPERA 3-D User Guide, Vector Fields Limited, Oxford,
England, (1999)
[9] Z a k r z e w s k i K . , T o m c z u k B . , K o t e r a s D . , Simulation
of forces and 3D field arising during power autotransformer
fault due to electric arc in HV winding, IEEE Trans. Magn., 38,
(2002), n. 2, 1153-1156
Autorzy: prof. dr hab. inż. Bronisław Tomczuk, Politechnika
Opolska, Katedra Elektrotechniki Przemysłowej, ul. Luboszycka 7,
456-036 Opole, E-mail: [email protected];, dr inż. Dariusz
Koteras,
Politechnika
Opolska,
Katedra
Elektrotechniki
Przemysłowej, ul. Luboszycka 7, 456-036 Opole, E-mail:
[email protected]
PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 85 NR 3/2009
99