Parametry materiałów półprzewodnikowych Temperatury

Projekt „NEW-TECH Program rozwoju praktycznych kompetencji nauczycieli zawodów branż
nowych technologii” jest współfinansowany przez Unię Europejską
WARSZTAT
Wybrane zagadnienia współczesnej elektroniki
Projekt realizowany przez COMBIDATA Poland sp. z o.o. w ramach umowy o dofinansowanie projektu w ramach Programu Operacyjnego
Kapitał Ludzki 2007-2013, Priorytetu III „Wysoka jakość systemu oświaty”, Działanie 3.4 „Otwartość systemu edukacji w kontekście uczenia
się przez całe życia” , Poddziałanie: 3.4.3 „Upowszechnienie uczenia się przez całe życie - projekty konkursowe”.
Plan warsztatów
•
•
•
Zjawiska termiczne w elementach półprzewodnikowych i układach elektronicznych
(Wykład, 2h)
Modelowanie układów elektronicznych w programie SPICE (Wykład, 2h)
Pomiary charakterystyk elementów półprzewodnikowych (Wykład, 2h)
Siedziba Akademii Morskiej
• Modelowanie układów elektronicznych w programie SPICE
(Laboratorium, 2h, sala C-248)
• Pomiary charakterystyk elementów półprzewodnikowych
(Laboratorium, 1h, sala C-218)
• Technika światłowodowa (Laboratorium, 1h, sala C-135)
• Technika laserowa (Laboratorium, 1h, sala C-135)
• Źródła promieniowania optycznego (Laboratorium, 1h, sala C-135)
• Detektory promieniowania optycznego (Laboratorium, 1h, sala C-135)
• Komputerowe projektowanie obwodów drukowanych układów elektronicznych
(Laboratorium, 5h, sala C-248)
Zjawiska termiczne w elementach
i układach elektronicznych
Plan referatu
 Parametry materiałów półprzewodnikowych
 Status komercyjny elementów półprzewodnikowych
 Charakterystyki izotermiczne elementów
półprzewodnikowych
 Zjawisko samonagrzewania
 Parametry termiczne i metody ich pomiaru
 Charakterystyki nieizotermiczne elementów
półprzewodnikowych
Parametry materiałów półprzewodnikowych
Materiały półprzewodnikowe we współczesnej elektronice
Moc [W]
1000
C?
SiC
100
Si – krzem
SiC – węglik krzemu
SiGe – krzemogerman
GaAs – arsenek galu
GaN – azotek galu
InP – fosforek indu
C – diament, grafen
GaN
Si
10
SiGe
GaAs
InP
100
1
10
Częstotliwość [GHz]
1000
Parametry materiałów półprzewodnikowych
Szerokość przerwy energetycznej (Wg, Eg)
Inne nazwy: wysokość bariery, szerokość obszaru zabronionego
Model pasmowy (*)
Parametr
Wg, Eg [eV]
* http://putwiki.informatyka.org
Si
1,21
InP
1,35
Wartość
GaAs
SiC (4H)
1,42
3,23
GaN
3,39
C
5,6
Parametry materiałów półprzewodnikowych
Szerokość przerwy energetycznej (Wg, Eg)
Zależność szerokości przerwy energetycznej od temperatury:
a)
a  T2
E g (T)  E g (0) 
bT
Eg(0) - szerokość przerwy energetycznej odpowiadająca temperaturze 0 K
Eg T   E g 0  0  T
Eg0 - wartość Eg ekstrapolowana do temperatury 0 K
p arametr
materiał
półprzewodnikowy
Eg(0)
[eV] dla
T=0K
Eg(300)
[eV] dla
T = 300 K
Eg0 [eV]
a [eV·K -1]
b [K]
α0 [eV·K -1]
Si
4H-SiC
GaN
1,170
3,265
3,470
1,1245
3,230
3,393
1,21
3,32
3,54
4,73·10-4
6,5·10-4
7,7·10-4
636
1300
600
0,000285
0,0003
0,00049
1,22
Si
b)
3.5
1,19
3.45
1,16
Eg [eV]
Eg [eV]
3.55
1,13
3.4
3.35
1,1
3.3
1,07
3.25
1,04
3.2
0
100
200
300
400
T [K]
500
600
GaN
4H-SiC
0
100
200
300
400
T [K]
500
600
Parametry materiałów półprzewodnikowych
Koncentracja nośników samoistnych (ni)
Zależność koncentracji samoistnej od temperatury:
Eg0 

3

n i  A 0  T 2  exp  
2

k

T


Parametr
Si
InP
10
1,510
1,3107
-3
ni [cm ]
15 milionów swobodnych
elektronów i dziur w 1 mm3
A0 – parametr materiałowy niezależny od temperatury
k – stała Boltzmanna
Wartość (w 300 K)
GaAs
SiC (4H)
6
2,110
510-9
!
-3
ni [cm ]
6
10
0
10
10-6
10-12
Si
GaAs
4H-SiC
GaN
C
10-18
10-24
10-30
100 200 300 400 500 600 700 800 900 1000
T [K]
C
10-27
1 swobodny elektron i 1 dziura w bryle
o objętości 5000 m3
Uwaga! Koncentracja atomów krzemu = 1023 cm-3
1018
1012
GaN
110-11
!
Parametry materiałów półprzewodnikowych
Ruchliwość nośników
Zależność prędkości nośników od natężenia pola elektrycznego:
vS – prędkość nośników
E – natężenie pola elektrycznego
vS    E
Parametr
n [cm /Vs]
p [cm2/Vs]
vS [cm/s]
2
Si
1400
450
1107
InP
6000
200
2107
Wartość
GaAs
SiC (4H)
8000
900
400
120
7
110
2107
GaN
1000
350
2,5107
10
7
vS [10 cm/s]
4H-SiC
GaAs
1
Si
GaN
6H-SiC
0,1
1
10
E [kV/cm]
100
1000
C
2200
1800
3·107
Parametry materiałów półprzewodnikowych
Ruchliwość nośników
W literaturze podano wiele modeli μ(T, N, E):
1967 r., Caughey i Thomas:
( N)   min 
 max   min
 N

1  
N
 0
1
1977 r., Jacoboni:
max  min 
1999 r., Benda:
5,1  10  92  N
n ( ND ) 
3,75  1015  N
18
   min 
0 , 91
D
0 , 91
D
1  N / N 
2
0

 p  n  / 2  N 0
12
2,9  1015  47,7  N 0A, 76
p ( NA ) 
5,86  1012  N 0A, 76
Często stosowany model ruchliwości (*):
Si
GaN
GaAs
C
InP
μTn0
[cm2/(V∙s)]
1360
1000
8500
2100
4000
μT0 - ruchliwość elektronów lub dziur w temperaturze T0
α - wskaźnik zależny od rodzaju półprzewodnika i rodzaju nośników
a) 10000
parametr
μTp0
αn
[cm2/(V∙s)]
495
2,42
170
2
400
1,1
1700
1,37
180
1,42
αp
2,2
5
2,1
1,5
2,5
elektrony
GaAs
8000
6000
2
materiał

μn [cm /(V∙s)]
T
   T 0   
 T0 
lnP
C
4000
Si
2000
GaN
0
200
* Baliga B. J.: Modern Power Devices. John Wiley and Sons, New York, 1987
250
300
350
400
T [K]
450
500

2

Parametry materiałów półprzewodnikowych
Konduktywność elektryczna (przewodność elektryczna właściwa)
Półprzewodnik samoistny:
Półprzewodnik domieszkowany:
i  q  n i  n   p 
  q  n   n  p   p 
q - ładunek elementarny, n, p - koncentracje swobodnych elektronów i dziur, natomiast, µn, µp - ich ruchliwość
W przypadku konduktywności samoistnej, zakładając niezależność parametrów µ oraz ni od koncentracji domieszek oraz
przyjmując temperaturowe zależności tych parametrów, a także przyjmując taką samą wartość parametru materiałowego α
równą 3/2 we wzorze na μ(T) dla elektronów i dla dziur (αp= αn), otrzymujemy:
Eg0 


i T   B  exp 
2

k

T


gdzie B oznacza parametr niezależny od temperatury, dany wzorem :
T [K]
0
200
400
 n 0  p0 

B  q  A1  
300


600
800
σi [1/Ω·cm]
10-1
10-6
10-11
10
10
-16
-21
10-26
Si
GaN
InP
GaAs
C
1000
w którym A1 jest parametrem
Parametry materiałów półprzewodnikowych
Krytyczne natężenie pola elektrycznego
2,6
EC [kV/cm]
350
4H-SiC [500 K]
InP [500 K]
300
2,4
2,2
250
2
Si [500 K]
200
1,8
Si [300 K]
150
1,6
100
10
17
18
10
b)
4H-SiC [300 K]
InP [300 K]
18
10
N [cm-3]
1019
1020
NB – koncentracja domieszki
1,4
550
500
450
400
350
300
250
200
150
100
C
7
GaAs
6
InP
5
Si
4
GaN
4H-SiC
0
200
400
600
T [K]
800
3
2
1000
EC [MV/cm]
400
EC [MV/cm]
a)
q
3/ 4
 N1B/ 8  E g
S
EC [kV/cm]
E C  1,02  107 
Parametry materiałów półprzewodnikowych
Temperatury charakterystyczne – temperatura wtórnej samoistności
Ważnym parametrem termicznym określającym możliwości wykorzystania materiału półprzewodnikowego w
wysokich temperaturowych jest temperatura wtórnej samoistności TS, w której koncentracja samoistna jest równa
koncentracji domieszki.
1024
ni [cm-3]
4H-SiC
10
15
10
6
10
-3
ND = 1015 cm-3
Si
C
GaAs
GaN
10-12
10-21
10-30
-100 100 300 500 700 900 1100 1300 1500 1700 1900
TS[°C]
T [C]
2000
1750
1500
1250
1000
750
500
250
0
N = 1014cm-3
C
GaN
4H-SiC
6H-SiC
3C-SiC
GaAs
Si
1
2
3
Eg [eV]
4
5
6
Parametry materiałów półprzewodnikowych
Temperatury charakterystyczne – temperatura topnienia
Potencjalne możliwości zastosowania materiału półprzewodnikowego w wysokich temperaturach określa jego
temperatura topnienia Tt.
Temperatura topnienia wybranych elementów półprzewodnikowych.
Tt [°C]
4000
Eg
3300
3100
3000
2000
1690
1510
1740
1800
1210
1000
0
Ge
Si
GaAs
GaP 6H-SiC GaN
C
Parametry materiałów półprzewodnikowych
Przewodność cieplna właściwa
Gęstość strumienia ciepła ΦC przepływającego na skutek przewodnictwa ciepła jest proporcjonalna do gradientu
temperatury
 C    grad T
Współczynnik proporcjonalności λ oznacza przewodność (konduktywność) cieplną właściwą.
Parametr
Si
1,3
30
-1
20
10
13
10
1E+13
14
10
1E+14
15
10
1E+15
N[cm-3]
16
10
1E+16
GaN
1,1
b) 1000
diament
T = 300 K
0 12
10
1E+12
Wartość
SiC (4H)
7
1 1
W?cm ?K 
40
-1
a)
 [W∙cm ∙K ]
th [W/cmK]
GaAs
0,55
17
10
1E+17
C
20
diament
100
10
1
1
10
T [K]
100
1000
Parametry materiałów półprzewodnikowych
Wskaźniki jakości materiałów półprzewodnikowych (Figures of Merit)
Aby ocenić przydatność oraz dokonać optymalnego wyboru materiału półprzewodnikowego do konstrukcji różnych
elementów o różnym przeznaczeniu (na przykład duża moc, wysoka częstotliwość pracy itp.), zdefiniowano szereg tzw.
wskaźników jakości FOMs (Figures of Merit)
1965 r., Johnson:
1972 r., Keyes:
1982 r., Baliga:
1989 r., Baliga:
1989 r., Shenai:
JFOM 
KFOM   
BFOM  s    E3C
BHFOM    EC2
TQFOM    
E C  v sat
2
c  vsat
4    s
Znormalizowane wartości FOMs.
2004 r., Huang:
1000
JFOM
KFOM
BFOM
BHFOM
TQFOM
HTFOM
HCAFOM
HMFOM
4H-SiC
6H-SiC
3C-SiC
GaAs
Si

s  E C
2005 r., Huang:
100
HCAFOM   s    E C2
2005 r., Baliga:
10
1
GaN
HTFOM 
0,1
HMFOM  E C  
Status komercyjny elementów półprzewodnikowych
Czołowi producenci elementów elektronicznych wykonanych
z nowoczesnych materiałów półprzewodnikowych
Status komercyjny elementów półprzewodnikowych
Diody Schottky’ego z węglika krzemu (SiC Schottky)



około 70 typów diod
600 V, 650 V, 1200 V, 1700 V
różne rodzaje obudów
Przykład: dioda o symbolu C3D25170H
zaskakująco niska Tj !
* http://www.cree.com
Status komercyjny elementów półprzewodnikowych
Tranzystory MOS z węglika krzemu (SiC MOSFET)


7 typów tranzystorów
1200 V, 1700 V
Status komercyjny elementów półprzewodnikowych
Tranzystory HEMT z azotku galu (GaN HEMT)

około 40 typów tranzystorów
Status komercyjny elementów półprzewodnikowych



SiC Schottky
około 60 typów
600 V, 650 V, 1200 V


SiC Schottky (około 12 typów)
SiC MOSFET (1 typ)


SiC JFET (4 typy)
Od 2011 r. działalność firmy zawieszona

SiC BJT (2 typy)



SiC Schottky (około 9 typów)
SiC MOSFET (6 typów)
SiC Thyristor (4 typy)
Charakterystyki izotermiczne elementów półprzewodnikowych
 Charakterystyki izotermiczne – tzn. w stałej temperaturze
 Idealne warunki chłodzenia, Tjunction = Tambient
 Pomiary charakterystyk izotermicznych

pomiary impulsowe (problem doboru czasu trwania impulsu)

dodatkowe chłodzenie elementu
 Izotermiczne charakterystyki katalogowe – typowo w 25C
 Charakterystyki izotermiczne nie odzwierciedlają „rzeczywistych”
warunków pracy elementu półprzewodnikowego
Charakterystyki izotermiczne elementów półprzewodnikowych
Dioda Schottky’ego
OnSemiconductor
Cree, Inc.
4,0
MBR1045
Si
pomiary
3,0
model autorski
2,5
model wbudowany
pomiary
3,5
model autorski
3,0
150oC
2,0
CSD10030
4,0
IF [A]
3,5
100oC
1,5
21oC
model wbudowany
2,5
100oC
2,0
150oC
1,5
1,0
1,0
0,5
21oC
0,5
0,0
0,0
0,1
0,2
0,3
0,4
0,5
0,1
0,3
0,5
UF [V]
OnSemiconductor U [V]
R
Si
Cree, Inc.
5
300
0
model autorski
26 C
0,001
model wbudowany
z estymowanymi
parametrami
1
125oC
SiC
150
100
50
0
model wbudowany
1,E-06
pomiary
model autorski
0,01
0,1
200
CSD10030
o
75 C
250
UR [V]
1,E-07
0,0001
o
0,9
UF [V]
85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10
pomiary
0,7
1,E-05
o
100 C
1,E-04
21oC
1,E-03
10
1,E-02
100
MBR1045
1000
1,E-01
o
175 C
1,E+00
IR [mA]
0
IR [mA]
IF [A]
SiC
4,5
Charakterystyki izotermiczne elementów półprzewodnikowych
Dioda Schottky’ego
SiC
Infineon Technologies
SiC
Infineon Technologies
IDW40G65C5
IDW40G65C5
Charakterystyki izotermiczne elementów półprzewodnikowych
Tranzystor MOS
Si
IRF840
Vishay Siliconix




małe uGS - T↑ iD↑
duże uGS - T↑ iD↓
punkt autokompensacji
termicznej
SiC – zależności analogiczne
Charakterystyki izotermiczne elementów półprzewodnikowych
Tranzystor MESFET
California Eastern Laboratories
5
iD [A]
b)
NE650103M
6
Cree, Inc.
Ta= 293 K
4
-1 V
3
2
-2 V
1
Ta= 297 K
2
-2 V
1,5
-4 V
1
-6 V
0
0
2
4
6
8
10
0
12
10
3
UDS= 13 V
NE650103M
2,5
b)
UDS= 2 V
30
1,5
CRF24010
SiC
UDS= 30 V
B
1,2
GaAs
Ta= 399 K
1,5
Ta= 293 K
1
iD [A]
2
20
uDS [V]
uDS [V]
iD [A]
UGS= 0 V
Ta= 468 K
0,5
-2,5 V
0
a)
SiC
CRF24010
3
2,5
Ta= 413 K
UGS= 0 V
iD [A]
a)
GaAs
UDS= 5 V
Ta= 295 K
0,9
0,6
Ta= 420 K
A
A
0,5
0,3
0
B
0
-4
-3
-2
uGS [V]
-1
0
-12
-9
-6
uGS [V]
-3
0
Charakterystyki izotermiczne elementów półprzewodnikowych
Tranzystor bipolarny (BJT)
3,5
IB=150 mA
25C
60C
100C
3
iC [A]
Panasonic
Si
2SC5294
4
2,5
IB=50 mA
2
1,5
1
0,5
0
0
1
2
3
4
5
6
uCE [V]
BTSiC1206
9
7,5
25C
60C
100C
6
iC [A]
TranSiC
SiC
IB=150 mA
4,5
IB=50 mA
3
1,5
0
0
1
2
3
uCE [V]
4
5
6
Zjawisko samonagrzewania
Mechanizm zjawiska samonagrzewania
energia elektryczna
ciepło
temperatura wnętrza
parametry elektryczne
napięcia i prądy zaciskowe
Jednym z istotnych zjawisk zachodzących w elementach półprzewodnikowych jest zjawisko samonagrzewania,
skutkujące wzrostem temperatury wnętrza elementu powyżej temperatury otoczenia. Przyrost temperatury jest
spowodowany zamianą energii elektrycznej wydzielanej w tym elemencie na ciepło przy nieidealnych warunkach
chłodzenia.
Zjawisko samonagrzewania
Skutki zjawiska samonagrzewania
wzrost temperatury wnętrza
ograniczenie SOA
zmiana wartości parametrów elementów oraz układów
pogorszenie niezawodności elementów oraz układów
Zjawisko samonagrzewania
Mechanizmy odprowadzania (dostarczania) ciepła
 Konwekcja
 Promieniowanie
 Przewodnictwo
Zakładając, że dominującym mechanizmem w odprowadzaniu ciepła z wnętrza elementu jest
przewodnictwo, to czasowo-przestrzenny rozkład temperatury w elemencie półprzewodnikowym lub
układzie scalonym można uzyskać z modelu termicznego w postaci równania przewodnictwa ciepła
(model mikroskopowy). Równanie przewodnictwa ciepła wiąże przestrzenno-czasowy rozkład gęstości
g(r, t) generowanej mocy cieplnej z przestrzenno-czasowym rozkładem temperatury T(r, t) w strukturze
elementu, gdzie r oznacza wektor położenia.
div  grad Tr, t   gr, t   c d
Tr, t 
t
gdzie: λ - przewodność cieplna, c - ciepło właściwe materiału, d - gęstość materiału,
g - gęstość generowanej mocy cieplnej
Zjawisko samonagrzewania
Skupiony model termiczny
W praktyce inżynierskiej stosuje się modele termiczne o stałych skupionych, które stanowią uproszczenie
modeli o stałych rozłożonych, bowiem nie uwzględniają one przestrzennego rozkładu temperatury w
elemencie. Przy formułowaniu takiego modelu zakłada się, że temperatura całego obszaru czynnego w
elemencie jest jednakowa.
Wykorzystując skupiony model termiczny, zależność temperatury wnętrza elementu dyskretnego od mocy
wydzielanej w tym elemencie można opisać za pomocą całki splotu o postaci:
t
Tj ( t )  T0   Zth ( t  x )  p th ( x ) dx
0
gdzie T0 jest temperaturą odniesienia, Zth’(t) oznacza czasową pochodną przejściowej impedancji
termicznej, natomiast pth(t), to czasowy przebieg mocy cieplnej
Równanie dla stanu termicznie ustalonego upraszcza się do postaci:
Tj  T0  R th  p th
gdzie pth oznacza moc cieplną wydzielaną w elemencie w stanie ustalonym, natomiast Rth - rezystancję
termiczną tego elementu.
Tak więc, podstawowymi parametrami modeli termicznych o stałych skupionych są: przejściowa
impedancja termiczna oraz rezystancja termiczna, opisujące właściwości cieplne elementu odpowiednio
w stanach przejściowych i w stanie ustalonym.
Parametry termiczne i metody ich pomiaru
Parametry termiczne – definicje
Przejściową impedancję termiczną Zth(t) definiuje się jako odpowiedź termiczną elementu na pobudzenie
mocą w postaci uskoku Heaviside'a, to znaczy p(t) = P0∙1(t). Tak więc:
Z th ( t ) 
T( t ) Tj (t )  T0

P0
P0
gdzie ΔT(t) oznacza nadwyżkę temperatury wnętrza Tj(t) elementu ponad temperaturę odniesienia T0.
W zależności od przyjętej we wzorze wartości T0, można zdefiniować dwie, przydatne w praktyce,
przejściowe impedancje termiczne. Dla T0 = TC, co oznacza przyjęcie stałej temperatury obudowy, z
równania otrzymuje się przejściową impedancję termiczną złącze-obudowa Zthj-c(t). Natomiast w przypadku,
gdy T0 = Ta – stała temperatura otoczenia, wyznaczana jest przejściowa impedancja termiczna złączeotoczenie Zthj-a(t).
Rezystancja termiczna Rth elementu definiowana jest podobnie, jako iloraz nadwyżki temperatury wnętrza
ponad temperaturę odniesienia w stanie termicznie ustalonym, do wywołującej tę nadwyżkę mocy P0.
Zatem rezystancja termiczna elementu stanowi wartość asymptotyczną przejściowej impedancji termicznej
dla t →∞.
Na przykład, tranzystor IRF840: Rthj-c = 1C/W, Rthj-a = 62,5C/W
Jeżeli moc P0 = 2 W (PTOT = 125 W), a temperatura otoczenia wynosi 27C, temperatura wnętrza
tranzystora pracującego bez radiatora (w stanie termicznie ustalonym) może dochodzić do 152C.
(Uwaga! Tjmax = 150C)
Zjawisko samonagrzewania
Skupiony model elektrotermiczny – zasada formułowania


F1 u, i, par Tj   0
MODEL
ELEKTRYCZNY
Tj  f1 part, p th 
Tj
u, i
ETM
MODEL
GENERACJI
CIEPŁA
MODEL
TERMICZNY
pth
p th  f 2 u, i 
Parametry termiczne i metody ich pomiaru
Metody pomiaru parametrów termicznych
 metody niszczące

optyczne

chemiczne
 metody nieniszczące

elektryczne
Parametry termiczne i metody ich pomiaru
Metody optyczne
 wielopunktowe (kamery i skanery termowizyjne)
Zalety: - uzyskanie rozkładu temperatury, - przegląd dużych powierzchni, - odnajdywanie punktowych
źródeł ciepła
Wady: - różne współczynniki emisyjności różnych materiałów (chropowatość i barwa), -konieczność
pokrywania elementu badanego czarną farbą
Parametry termiczne i metody ich pomiaru
Metody optyczne
 jednopunktowe (pirometry optyczne)
Wady: - analogiczne, jak w przypadku czujników wielopunktowych, - uzyskiwana uśredniona wartość
temperatury ze stosunkowo dużej powierzchni, np.. koła o średnicy 5 mm.
Parametry termiczne i metody ich pomiaru
Metody chemiczne
Badany element (układ) pokrywany jest mieszaniną ciekłych kryształów
Zalety: - uzyskanie rozkładu temperatury
Wady: - niższa dokładność oraz zdolność rozdzielcza w porównaniu do metody optycznej
Parametry termiczne i metody ich pomiaru
Metody elektryczne
Określenie temperatury wnętrza elementu półprzewodnikowego w metodach elektrycznych przeprowadza
się z wykorzystaniem tzw. parametru termoczułego, tzn. wybranego elektrycznego parametru elementu
półprzewodnikowego, którego wartość zależy od temperatury. Przykładowo, parametrami termoczułymi
tranzystora bipolarnego mogą być: napięcie na złączu baza-emiter spolaryzowanym w kierunku
przewodzenia, współczynnik wzmocnienia prądowego oraz prądy zerowe. Z kolei, parametrami
termoczułymi tranzystora MOS mogą być: napięcie progowe, rezystancja dren-źródło w stanie włączenia,
prąd drenu w stanie włączenia oraz napięcie na przewodzącym złączu źródło-podłoże lub dren-podłoże
przy ustalonej wartości prądu drenu.
Rodzaje metod elektrycznych
metody stałoprądowe
Pomiar wartości parametru termoczułego (w zasadzie temperatury)
przeprowadza się w trakcie wydzielania mocy cieplnej.
Metoda kłopotliwa w realizacji.
metody impulsowe
Pomiar realizowany w trakcie wyłączenia mocy cieplnej.
Wiele odmian tej metody.
Parametry termiczne i metody ich pomiaru
Przykład metody elektrycznej
Metoda pomiaru wg. Oettingera i Blackburna (*) wykorzystująca tzw. krzywe chłodzenia na przykładzie
tranzystora MESFET z arsenku galu (NE650103M) oraz węglika krzemu (CRF24010).
Etap I – kalibracja charakterystyki termometrycznej
0,7
0,6
uGS [V]
b)
NE650103M
0,9
CRF24010
0,8
1
1
uGS[V]
a)
2
0,5
3
0,4
0,7
2
3
0,6
4
4
0,5
5
5
0,3
0,4
10
50
90
Ta [°C]
Nr
charakterystyki
1
2
3
4
5
130
170
10
NE650103M (rys. a)
Prąd bramki IG
[mA]
0,22
0,4
1
3
8
Parametr a
[mV/K]
-1,8
-1,79
-1,77
-1,64
-1,51
40
70
100
130
Ta [°C]
CRF24010 (rys. b)
Prąd bramki IG
[mA]
0,1
0,4
1
5
10
* Oettinger F. F., Blackburn D. L.: Semiconductor Measurement Technology: Thermal Resistance
Measurements, U. S. Department of Commerce, NIST/SP-400/86, 1990.
Parametr a
[mV/K]
-1,46
-1,33
-1,27
-1,17
-1,02
160
190
Parametry termiczne i metody ich pomiaru
Przykład metody elektrycznej – realizacja układowa metody
Układ polaryzacji tranzystora
Źródła
sterujące
S
D1 D2
MESFET
D
G
S
IH, IM, E
Ta=const
R
E
Przetwornik A/C
D
S1
S
G
D
S
G
D3 D4
IM
IH
W.P.
ADC574AKH
Sygnał z portu
równoległego komputera
Układ sterujący
Program
Port równoległy
(IEEE 1284)
RAM
HDD
PC
Etap II – nagrzewanie tranzystora badanego mocą o wartości P0
Klucz S1 i S2 rozwarty – przez tranzystor badany (dren-źródło) płynie prąd o wartości IM+IH
Etap III – studzenie tranzystora badanego – pomiar Tj(t)
Klucz S1 i S2 zwarty – przez tranzystor (złącze bramka-źródło) płynie prąd pomiarowy IM
S
S2
D
G
Parametry termiczne i metody ich pomiaru
Przykładowe wyniki pomiarów
Przebiegi Tj(t)
410
P0= 2,21 W
390
Tj [K]
b)
NE650103M
bez radiatora
P0= 1,46 W
370
P0= 0,61 W
330
P0= 0,31 W
Ta= 293 K
Ta= 293 K
P0= 2,03 W
P0= 1,29 W
P0= 1,06 W
370
P0= 0,35 W
310
290
290
0
200
400
600
800
1000
0
t [s]
NE650103M
70
60
50
40
30
20
10
0
200
400
600
800
1000
t [s]
Z th ( t ) 
Przebiegi Zthj-a(t)
T( t ) Tj ( t )  T0

P0
P0
b) 100
bez radiatora
Ta= 293 K
Zthj-a [K/W]
Zthj-a [K/W]
bez radiatora
P0= 2,72 W
410
330
a)
CRF24010
450
P0= 0,96 W
350
490
Tj [K]
a)
1
1. P0 = 0,31 W
2. P0 = 0,6 W
3. P0 = 0,96 W
4. P0 = 1,46 W
5. P0 = 2,21 W
5
CRF24010
bez radiatora
1
Ta= 293 K
80
60
1. P0 = 0,35 W
2. P0 = 0,51 W
3. P0 = 1,06 W
4. P0 = 1,49 W
5. P0 = 2,72 W
40
20
5
0
0
200
400
600
t [s]
800
1000
0
200
400
600
t [s]
800
1000
Parametry termiczne i metody ich pomiaru
Przykładowe wyniki pomiarów
68
Rthj-a [K/W]
c)
NE650103M
Ta= 293 K
bez radiatora
64
Rthj-a [K/W]
a)
343 K
60
56
363 K
94
bez radiatora
88
343 K
82
76
363 K
70
395 K
395 K
64
52
0
0,5
1
1,5
2
2,5
0
3
0,5
1
28
26
radiator A
Rthj-a [K/W]
Rthj-a [K/W]
d)
NE650103M
Ta= 293 K
343 K
24
22
20
363 K
Ta= 293 K
22
3
4
pth [W]
3
5
6
7
radiator A
343 K
20
18
363 K
2
2,5
CRF24010
16
1
2
24
395 K
18
0
1,5
pth [W]
pth [W]
b)
CRF24010
Ta= 293 K
0
395 K
2
4
6
pth [W]
8
10
Charakterystyki nieizotermiczne elementów półprzewodnikowych
Dioda Schottky’ego
kierunek przewodzenia
4,5
4,0
160
pomiary
3,0
1,5
o
Tc [oC]
2,0
model autorski
izotermiczny
150 C
120
25oC
100
99oC
80
60
1,0
RTH1 = 66 K/W
40
25oC
99oC
0,5
0,0
0,05
150oC
140
model autorski ETM
2,5
MBR1045
180
RTH1 = 66 K/W
3,5
pomiary
20
model autorski ETM
0
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0,5
0,1
0,2
0,2
0,3
0,3
UF [V]
0,4
0,4
0,5
0,5
UF [V]
kierunek zaporowy
UR [V]
70
65
60
55
50
45
40
35
30
25
20
15
10
5
0
180
0,0001
MBR1045
model autorski
izotermiczny
RTH1 = 66 K/W
model autorski ETM
MBR1045
160
125oC
0,001
140
pomiary
0,1
75oC
Tc [oC]
0,01
26oC
IR [mA]
IF [A]
200
MBR1045
120
100
pomiary
80
1
26oC
model autorski ETM
60
RTH1 = 66 K/W
10
40
100
20
o
125 C
0
10
20
30
40
UR [V]
50
60
70
Charakterystyki nieizotermiczne elementów półprzewodnikowych
Tranzystor bipolarny
Si
4
9
Ta=25 C
IB=250 mA
IB=100 mA
2
IB=50 mA
SiC
Ta=25 C
IB=150 mA
6
iC [A]
iC [A]
7,5
izotermiczne
nieizotermiczne
3
izotermiczne
nieizotermiczne
4,5
IB=100 mA
3
A
1
IB=50 mA
1,5
0
0
0
1
2
3
4
5
uCE [V]
dodatnie termiczne sprzężenie zwrotne
6
Tj= 51C
0
1
2
3
uCE [V]
ujemne termiczne sprzężenie zwrotne
4
Charakterystyki nieizotermiczne elementów półprzewodnikowych
Tranzystor MESFET
a)
6
izotermiczna
iD [A]
5
C1
NE650103M
radiator B
C2
4
D2
3
D3
D1
radiator A
2
UGS= 0 V
bez radiatora
1
Ta= 295 K
0
0
3
6
9
12
15
uDS [V]
Tj [K]
c)
NE650103M
640
590
540
490
440
390
340
290
Ta= 295 K
radiator A
bez radiatora
Tjmax
radiator B
UGS= 0 V
0
1
2
3
4
uDS [V]
5
6
7
Pomiary charakterystyk elementów
półprzewodnikowych
Plan referatu
 Laboratorium pomiarowe – koncepcja realizacji
 Charakterystyka i parametry wybranych urządzeń pomiarowych
 Przykładowe stanowiska pomiarowe
Laboratorium pomiarowe – koncepcja realizacji
Laboratorium umożliwia zrealizowanie pomiarów wielu rodzajów charakterystyk i
parametrów elementów półprzewodnikowych, w tym m. in.:
 pomiary izotermicznych oraz nieizotermicznych charakterystyk statycznych i
dynamicznych, a także charakterystyk pojemnościowych C(u) elementu
półprzewodnikowego,
 system pomiarowy 4200-SCS Semiconductor Characterization System
 źródła mierzące typu 2602A oraz 2410
 pomiary parametrów termicznych elementu półprzewodnikowego,
rezystancji termicznej oraz przejściowej impedancji termicznej,
 systemy pomiarowe własnej konstrukcji
 przetworniki pomiarowe
w
tym
 pomiary temperatury wnętrza elementu półprzewodnikowego oraz jego obudowy,
jak również badanie rozkładu temperatury na powierzchni obudowy elementu lub w
przypadku elementów nieobudowanych - rozkładu temperatury jego wnętrza,
 skaner termowizyjny
 pirometry
 czujniki temperatury (np. Pt-100).
Charakterystyka i parametry wybranych urządzeń pomiarowych
System pomiarowy 4200-SCS firmy Keithley
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – widok tylnej ścianki jednostki centralnej
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – testbox
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – przewody łączeniowe
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – Source Measure Units (SMUs)
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – przykłady układów pomiarowych charakterystyk elementów elektronicznych
 dioda
 tranzystor
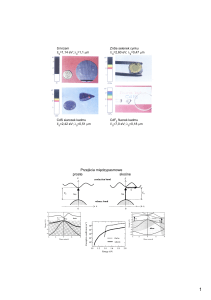
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – przykład impulsowego pomiaru charakterystyk tranzystora
Charakterystyka i parametry wybranych urządzeń pomiarowych
4200-SCS – przykład pomiaru pojemności tranzystora MOS
Charakterystyka i parametry wybranych urządzeń pomiarowych
Źródło mierzące 2602A System Source Meter
Charakterystyka i parametry wybranych urządzeń pomiarowych
Źródło mierzące 2602A System Source Meter
Charakterystyka i parametry wybranych urządzeń pomiarowych
Przykładowa konfiguracja pomiaru