ARYTMETYKA MODULARNA Grzegorz Szkibiel

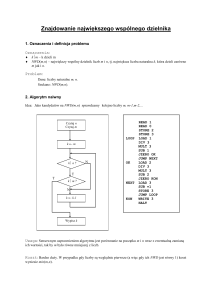
ARYTMETYKA MODULARNA
Grzegorz Szkibiel
Wiosna 2014/15
Spis tre±ci
1 Denicja kongruencji i jej podstawowe wªasno±ci
3
2 Systemy pozycyjne
8
3 Elementy odwrotne
12
4 Pewne zastosowania elementów odwrotnych
17
5 Maªe Twierdzenie Fermata
20
6 Twierdzenie Eulera
23
7 Twierdzenie Lagrange'a
27
8 Chi«skie Twierdzenie o Resztach
30
9 RSA i gra w orªa i reszk¦ przez telefon
34
10 Kongruencje wy»szych stopni
38
11 Liczby pseudopierwsze
44
12 Pierwiastki pierwotne
49
13 Istnienie pierwiastków pierwotnych
53
14 Logarytm dyskretny
58
15 Pewne zastosowania pierwiastków pierwotnych
61
2
Wykªad 8
Chi«skie Twierdzenie o Resztach
Twierdzenie, które tu przedstawimy zostaªo odkryte i wykorzystywane w ±redniowiecznych Chinach. Przyczyn¡ tego odkrycia byªy trudno±ci z mno»eniem i dodawaniem du»ych liczb ªatwiej jest nauczy¢ si¦ na pami¦¢ kilku
kombinacji, ni» wykonywa¢ dziaªania arytmetyczne w pami¦ci.
A dokªad-
nie, kiedy dowódca chciaª zliczy¢ swoje wojsko, kazaª ustawi¢ si¦ »oªnierzom
w dwu-szeregu, nast¦pnie w trzy-szeregu, potem w pi¦cio-szeregu itd. Liczba
,,niesparowanych »oªnierzy w ka»dym z tych ustawie« (czyli reszty z dzielenia
ogólnej liczby »oªnierzy przez 2, 3, 5, . . . ) dawaªy liczb¦ wszystkich »oªnierzy.
›eby skonkretyzowa¢ nasze my±lenie, rozwa»my nast¦puj¡cy przykªad.
8.1 Przykªad.
Po ustawieniu caªego wojska w 3-, 5- i 7-szeregu dostali±my,
odpowiednio 2, 1 oraz 6 niesparowanych »oªnierzy. Jaka jest liczebno±¢ oddziaªu, je»eli wiadomo, »e »oªnierzy jest mniej ni» 100?
Formalizuj¡c zadanie, niech
lenia
x
x b¦dzie liczb¡ »oªnierzy.
Zatem reszty z dzie-
przez 3, 5 oraz 7, to 2, 1 i 6. St¡d
x≡2
x≡1
x≡6
(mod 3)
(mod 5)
(mod 7)
(8.1)
(8.2)
(8.3)
Powy»szy ukªad trzech kongruencji rozwi¡»emy w nast¦puj¡cy sposób. Z kon-
x = 3k + 2. Podstawiaj¡c do (8.2), otrzymujemy 3k +
2 ≡ 1 (mod 5), czyli 3k ≡ −1 (mod 5). Znajdujemy liczb¦ odwrotn¡ do 3
modulo 5 i rozwi¡zujemy ostatni¡ kongruencj¦ otrzymuj¡c k ≡ −2 (mod 5).
Zatem k = 5r −2 oraz x = 3·(5r −2)+2 = 15r −4. Podstawiaj¡c t¦ posta¢ x
do (8.3) dostajemy 15r − 4 ≡ 6 (mod 7), a nast¦pnie r ≡ 3 (mod 7). St¡d
gruencji (8.1) mamy
30
mamy
r = 7s + 3,
czyli
x = 15 · (7s + 3) − 4 = 105s + 41.
Zatem wszystkich
»oªnierzy jest 41 (nast¦pna mo»liwo±¢ to 146, ale jak zaznaczyli±my, »oªnierzy
jest mniej ni» 100).
Dowódca, oczywi±cie, nie musiaª przeprowadza¢ powy»szych rachunków,
a jedynie zapami¦ta¢, »e ukªadowi 2-1-6 odpowiada liczba 41. Pami¦taª on
te» zapewne, jakim ukªadom odpowiadaj¡ s¡siednie liczby:
ukªad
liczba
ukªad
liczba
2-0-0
35
2-1-6
41
0-1-1
36
0-2-0
42
1-2-2
37
1-3-1
43
2-3-3
38
2-4-2
44
0-4-4
39
0-0-3
45
1-0-5
40
1-1-4
46
Ide¦ powy»szego przykªadu uogólnimy i podamy w dowodzie nast¦puj¡cego twierdzenia.
8.2 Twierdzenie
m2 , . . . , mr
(Chi«skie twierdzenie o resztach)
.
Przypu±¢my, »e
x ≡ a1 (mod m1 )
x ≡ a2 (mod m2 )
..................
x ≡ ar (mod mr )
ma jednoznaczne rozwi¡zanie modulo
xi = Mi−1 mod mi
dla
1 ≤ i ≤ r.
(8.4)
m1 m2 . . . mr .
Dowód. Wprowad¹my nast¦puj¡ce oznaczenia:
oraz
m1 ,
s¡ parami wzgl¦dnie pierwsze. Wówczas ukªad kongruencji
M = m1 m2 . . . mr , Mi =
M
,
mi
Rozwa»my teraz liczb¦
x = a1 M1 x1 + a2 M2 x2 + · · · + ar Mr xr .
j ̸= i zachodzi Mj ≡ 0 (mod xi ), wi¦c x ≡ ai Mi xi (mod mi )
dla ka»dego i. Ale Mi xi ≡ 1 (mod mi ), wi¦c x ≡ ai (mod mi ) dla 1 ≤ i ≤ r .
′
′′
Pozostaje jeszcze udowodni¢ jednoznaczno±¢.
Niech x oraz x b¦d¡
′
′′
dwoma rozwi¡zaniami ukªadu (8.4). Zatem x ≡ x (mod mi ) dla 1 ≤ i ≤ r .
′
′′
St¡d mi | x − x , a poniewa» m1 , m2 , . . . mr s¡ parami wzgl¦dnie pier′
′′
wsze, wi¦c M | x − x . Zatem dwa rozwi¡zania ukªadu (8.4) ró»ni¡ si¦ o
wielokrotno±¢ M i ukªad ten ma jednoznaczne rozwi¡zanie modulo M .
Poniewa» dla
31
W odró»nieniu od dowodów wielu innych podobnych twierdze«, dowód
chi«skiego twierdzenia o resztach daje wzór na rozwi¡zanie ukªadu kongruencji typu (8.4).
8.3 Przykªad.
Rozwa»my ukªad kongruencji z przykªadu 8.1.
oznaczenia dowodu twierdzenia 8.2, mamy
M = 105
i
mi
ai
Mi
xi
1
3
2
35
2
2
5
1
21
1
3
7
6
15
1
Stosuj¡c
oraz
St¡d
x ≡ 2 · 35 · 2 + 1 · 21 · 1 + 6 · 15 · 1
≡ 140 + 21 + 90
≡ 251
≡ 41
(mod
(mod
(mod
(mod
105)
105)
105)
105).
Zaªo»enie o kopierwszo±ci moduªów jest do±¢ istotnym ograniczeniem.
Rozwa»my dla przykªadu, ukªad kongruencji
x ≡ 3 (mod 8)
x ≡ 7 (mod 12).
(8.5)
Nie mo»na go rozwi¡za¢ stosuj¡c twierdzenie 8.2, poniewa» 8 oraz 12 nie s¡
wzgl¦dnie pierwsze. Nie oznacza to jednak, »e ukªad ten nie ma rozwi¡zania.
Rozwi¡»emy go w nast¦pnym przykªadzie.
8.4 Przykªad.
12 = 4 · 3
Aby rozwi¡za¢ ukªad kongruencji (8.5) zapiszmy najpierw
i rozbijmy drug¡ kongruencj¦ ukªadu na dwie kongruencje
x ≡ 7 ≡ 3 (mod 4)
i
x ≡ 7 ≡ 1 (mod 3).
Mamy zatem ukªad trzech kongruencji
x≡3
x≡3
x≡1
(mod 8)
(mod 4)
(mod 3).
32
(8.6)
Ale rozwi¡zanie pierwszej kongruencji ukªadu (8.6) speªnia te» drug¡ kongruencj¦, wi¦c druga kongruencja jest niepotrzebna.
Otrzymujemy wi¦c
równowa»ny (8.5) ukªad kongruencji
x≡3
x≡1
(mod 8)
(mod 3).
Ostatni ukªad rozwi¡zujemy stosuj¡c chi«skie twierdzenie o resztach (8.2) i
otrzymujemy
x ≡ 19 (mod 24).
Podamy teraz uogólnienie chi«skiego twierdzenia o resztach, które pozwala rozwi¡zywa¢ ukªady kongruencji podobne do (8.5).
8.5 Twierdzenie.
Przypu±¢my, »e
m1 , m2 . . . , mr
s¡ liczbami naturalnymi.
Wówczas ukªad kongruencji (8.4) ma rozwi¡zanie wtedy i tylko wtedy, gdy
(mi , mj ) | ai − aj dla i ̸= j .
modulo NWW(m1 , m2 , . . . , mr ).
NWD
Otrzymane rozwi¡zanie jest jednoznaczne
Dowód. Rozwa»my najpierw przypadek, gdy mi
= pei , gdzie 1 ≤ i ≤ r, ei jest
p jest liczb¡ pierwsz¡. Mo»emy, oczywi±cie, zaªo»y¢,
»e e1 ≥ e2 ≥ · · · ≥ er . Przypu±¢my teraz, »e taki ukªad kongruencji ma
e
rozwi¡zanie x0 i niech i < j . Zatem NWD(mi , mj ) = mj = p j . Skoro zachodz¡
ei
ej
e
kongruencje x0 ≡ ai (mod p ) oraz x0 ≡ aj (mod p ), wi¦c p j dzieli x0 −aj
e
e
e
e
oraz, poniewa» p j | p i , p j dzieli tak»e x0 − aj . St¡d p j | ai − aj .
e
W drug¡ stron¦, je±li i < j , to rozwi¡zanie kongruencji x0 ≡ ai (mod p i )
ej
jest te» rozwi¡zaniem kongruencji x0 ≡ aj (mod p ), wi¦c, w szczególe
no±ci, rozwi¡zanie pierwszej kongruencji (jednoznaczne modulo p 1 ) jest te»
liczb¡ nieujemn¡, a
rozwi¡zaniem pozostaªych kongruencji. Aby zako«czy¢ t¦ cz¦±¢ dowodu, zae
uwa»my jeszcze, »e p 1 = NWW(m1 , m2 , . . . , mr ).
Przejd¹my teraz do ogólnego przypadku. Zapiszmy
m1 = pe111 pe212 . . . pke1k
m2 = pe121 pe222 . . . pke2k
..................
mr = pe1r1 pe2r2 . . . pekrk .
Wówczas ukªad kongruencji (8.4) jest równowa»ny ukªadowi, skªadaj¡cemu
33
si¦ z podukªadów postaci
x ≡ a1 (mod pes1s )
x ≡ a2 (mod pes2s )
..................
x ≡ ar (mod pesrs ),
es = max {ets : 1 ≤ t ≤ r}. Ka»dy z pode
ukªadów (8.7) ma jednoznaczne modulo pss rozwi¡zanie wtedy i tylko wtedy,
( eis ejs )
gdy NWD ps , ps
| ai − aj dla i ̸= j , co wynika z pierwszej cz¦±ci dowodu.
Co wi¦cej, rozwi¡zanie ys tego podukªadu jest rozwi¡zaniem kongruencji o
e
module pss , wi¦c ukªad (8.4) jest równowa»ny ukªadowi
gdzie
1 ≤ s ≤ k.
(8.7)
Oznaczmy
x ≡ y1 (mod pe11 )
x ≡ y2 (mod pe22 )
..................
x ≡ yk (mod pekk ).
(8.8)
Ostatni ukªad ma rozwi¡zanie z uwagi na chi«skie twierdzenie o resztach
oraz, je±li rozwi¡zanie istnieje, to jest ono jednoznaczne modulo
pe11 pe22 . . . pekk = NWW(m1 , m2 , . . . , mr ).
Poniewa» rozwi¡zanie ukªadu (8.4) przy zaªo»eniach dowodzonego twierdzenia
jest równowa»ne rozwi¡zaniu ukªadu (8.8), wi¦c twierdzenie jest udowodnione.
Powy»szy dowód podaje te» sposób na rozwi¡zanie ukªadu kongruencji.
Sposób ten zostaª ju» zademonstrowany w przykªadzie (8.4). Dla utrwalenia
rozwi¡»my jeszcze jeden ukªad kongruencji.
8.6 Przykªad.
Ukªad kongruencji
x ≡ 5 (mod 8)
x ≡ 7 (mod 14)
x ≡ 21 (mod 35)
34
ma rozwi¡zanie, poniewa» zachodzi NWD(8,
(8, 14) | 5 − 7.
NWD
35) = 1,
NWD
(14, 35) | 7 − 21
oraz
Aby rozwi¡za¢ nasz ukªad zapisujemy
8 = 23 · 50 · 70
14 = 21 · 50 · 71
35 = 20 · 51 · 71
i zast¦pujemy ukªadem równowa»nym (przy czym pomijamy kongruencje o
module 1)
x ≡ 5 (mod 8)
x ≡ 7 (mod 2)
x ≡ 21 (mod 5)
x ≡ 7 (mod 7)
x ≡ 21 (mod 7)
Rozwi¡zaniami trzech podukªadów s¡ odpowiednio 5, 1 oraz 0. Zatem nasz
ukªad kongruencji sprowadza si¦ do ukªadu
x≡5
x≡1
x≡0
(mod 8)
(mod 5)
(mod 7),
który rozwi¡zujemy stosuj¡c chi«skie twierdzenie o resztach i otrzymujemy
rozwi¡zanie
x = 21
jednoznaczne modulo 280.
35