6. OBWODY PRĄDU ZMIENNEGO - WIADOMOŚCI PODSTAWOWE

6. OBWODY PRĄDU ZMIENNEGO - WIADOMOŚCI PODSTAWOWE
6.1. Klasyfikacja prądów ze względu na zmienność w czasie
Prąd zmienny jest to taki prąd, którego natężenie zmienia się w czasie. Podstawowymi
parametrami służącymi do opisywania podobnych, zależnych od czasu zjawisk fizycznych, są
wartości charakteryzujących je wielkości w konkretnej, rozważanej chwili czasowej, zwane
wartościami chwilowymi. W technice przyjęto jako normę, że wartości chwilowe oznacza się
małymi literami (np.: i, u, v, e, j). Istnieją jednak zwyczajowe wyjątki od tej reguły. Na przykład
wartości chwilowe wielkości opisujących pole magnetyczne oznacza się dużymi literami „H”
(natężenie), „B” (indukcja), „Φ” (strumień magnetyczny). Aby uniknąć ewentualnych
nieporozumień (możliwych zwłaszcza
wtedy, gdy wartość chwilowa oznaczona
jest dużą literą) zastosowany symbol
można uzupełnić literą „t” w nawiasie
(np.: i(t), u(t), v(t), e(t), j(t), H(t), B(t),
Φ(t)). Otrzymany w ten sposób symbol
jest jednocześnie symbolem wartości
chwilowej (w chwili czasowej „t”) oraz
symbolem zależności funkcyjnej danej
wielkości od czasu.
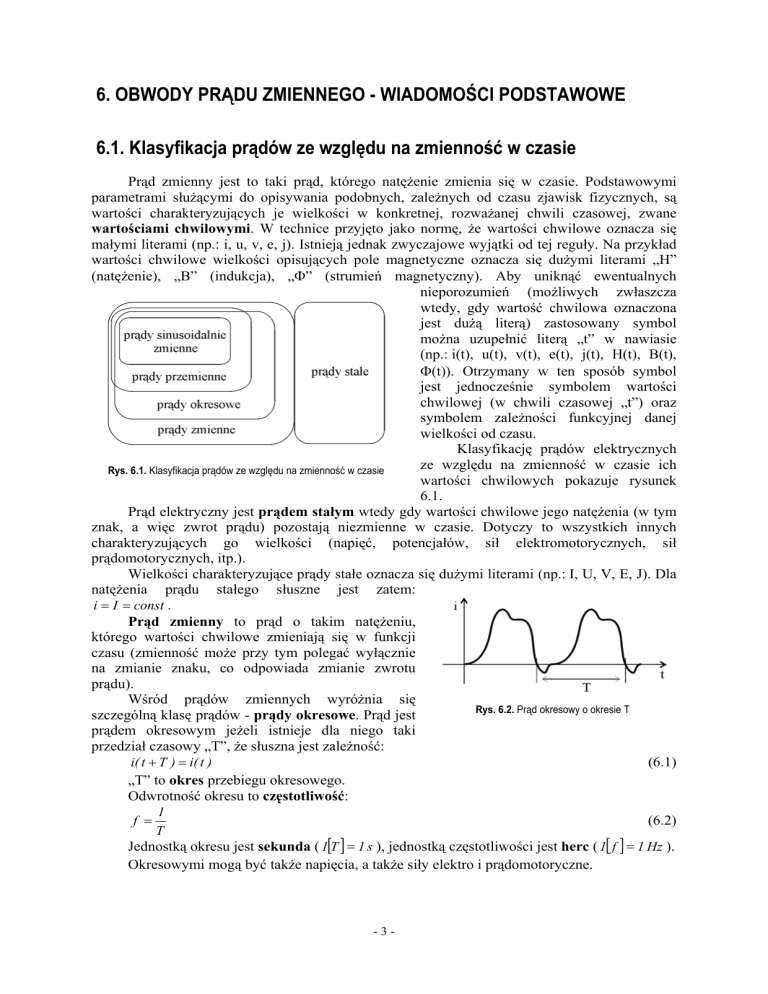
Klasyfikację prądów elektrycznych
ze
względu
na zmienność w czasie ich
Rys. 6.1. Klasyfikacja prądów ze względu na zmienność w czasie
wartości chwilowych pokazuje rysunek
6.1.
Prąd elektryczny jest prądem stałym wtedy gdy wartości chwilowe jego natężenia (w tym
znak, a więc zwrot prądu) pozostają niezmienne w czasie. Dotyczy to wszystkich innych
charakteryzujących go wielkości (napięć, potencjałów, sił elektromotorycznych, sił
prądomotorycznych, itp.).
Wielkości charakteryzujące prądy stałe oznacza się dużymi literami (np.: I, U, V, E, J). Dla
natężenia prądu stałego słuszne jest zatem:
i = I = const .
Prąd zmienny to prąd o takim natężeniu,
którego wartości chwilowe zmieniają się w funkcji
czasu (zmienność może przy tym polegać wyłącznie
na zmianie znaku, co odpowiada zmianie zwrotu
prądu).
Wśród prądów zmiennych wyróżnia się
Rys. 6.2. Prąd okresowy o okresie T
szczególną klasę prądów - prądy okresowe. Prąd jest
prądem okresowym jeżeli istnieje dla niego taki
przedział czasowy „T”, że słuszna jest zależność:
(6.1)
i( t + T ) = i( t )
„T” to okres przebiegu okresowego.
Odwrotność okresu to częstotliwość:
1
(6.2)
f =
T
Jednostką okresu jest sekunda ( 1[T ] = 1 s ), jednostką częstotliwości jest herc ( 1[ f ] = 1 Hz ).
Okresowymi mogą być także napięcia, a także siły elektro i prądomotoryczne.
-3-
Prąd przemienny to taki prąd zmienny okresowy, którego natężenie przyjmuje wartości
dodatnie i ujemne (płynie raz w jedną raz w drugą stronę) i dla którego słuszna jest zależność:
T
∫ i( t )dt = 0
(6.3)
0
6.2. Wartość średnia, wartość skuteczna
Dla przebiegów okresowych można zdefiniować wartości opisujące przebieg „całościowo”,
za cały okres. Takimi wartościami są wartości średnie i wartości skuteczne danych wielkości
(natężeń, napięć, potencjałów, itp).
Wartość średnia wielkości okresowej jest to średnia arytmetyczna przebiegu czasowego
tej wielkości za okres. Dla prądu, fizycznie jest to natężenie takiego umyślonego prądu stałego,
który w czasie jednego okresu przenosi taki sam ładunek jak dany prąd okresowy.
Wartość średnią oznacza się dużą literą z indeksem „av” albo z umieszczoną u góry kreską
(np.: I av albo I ).
Wyznacza się ją (tu przykładowo wartość średnią natężenia prądu) z zależności:
T
I av ≡ I =
1
⋅ i( t )dt
T ∫
(6.3)
0
Dla przebiegu sinusoidalnego, a takie przebiegi okresowe najczęściej występują w praktyce,
jest:
I av =
1
2π
2π
⋅
∫ I m sin( ωt )dωt =
0
Im
2π
2π
⋅ ( − cos( ωt )
=
0
Im
2π
⋅ [− 1 − ( −1 )] = 0
(6.3a)
Wartość średnia przebiegu sinusoidalnego wynosi zatem zero. Z tego powodu pojęcie
wartości średniej niezbyt nadaje się do opisywania prądów sinusoidalnie zmiennych. Wynikła
stąd potrzeba znalezienia wielkości bardziej do tego przydatnej. Taką „bardziej przydatną”
wielkością jest wartość skuteczna.
Historycznie koncepcja wartości skutecznej związana jest z przyrządami pomiarowymi
cieplikowymi (cieplnymi), obecnie stosowanymi bardzo rzadko. Są to przyrządy, które do pomiaru
wielkości elektrycznych wykorzystują zjawisko nagrzewania się przewodnika na skutek
przepływu prądu. Najważniejszą ich częścią jest drucik grzejny, przez który przepływa mierzony
prąd. Temperatura do jakiej nagrzewa się taki
drucik zależy od natężenia prądu. W tradycyjnych
rozwiązaniach miernika, do jej pomiaru
wykorzystywane jest zjawisko rozszerzalności
cieplnej materiału (por. rys. 6.3.). Temperatura ta,
a w związku z tym także wskazanie miernika, nie
zależy od zwrotu prądu. Stąd przyrząd cieplikowy
można wyskalować prądem stałym, a następnie
używać do pomiaru prądu zmiennego. To co
wskazuje taki przyrząd nazwano wartością
skuteczną (bo daje taki sam skutek energetyczny
Rys. 6.3. Budowa miernika cieplikowego
1. drucik grzejny, 2. tzw. „mostek”,
jak prąd stały, którego użyto do skalowania
3. nić jedwabna, 4. rolka ze wskazówką,
przyrządu). Jeszcze w latach 1930-tych wartości
5. sprężyna napinająca
skuteczne określane bywały jako „wartości
wskazywane przez przyrządy cieplikowe”.
Zgodnie ze współczesną definicją, wartość skuteczna natężenia prądu okresowego jest to
natężenie takiego umyślonego prądu stałego, który, przepływając przez rezystor o nie
zmieniającej się rezystancji, wydzieliłby na nim, w czasie jednego okresu, lub jego
-4-
wielokrotności, taką samą ilość energii cieplnej, jaką, w tym samym czasie, wydziela dany prąd
okresowy.
Z definicji tej wynika wzór na obliczanie wartości skutecznej natężenia prądu okresowego:
Stąd otrzymuje się poszukiwany wzór:
energia cieplna pobrana przez rezystor
o rezystancji R, w którym płynie prąd
okresowy i( t ) o okresie T:
energia cieplna pobrana przez rezystor
o rezystancji R, w którym płynie
umyślony prąd stały I:
WT = R ⋅ I 2 ⋅ T
T
=
⇓
WT = ∫ R ⋅ i( t )2 dt
0
T
2
R ⋅ I ⋅ T = ∫ R ⋅ i( t )2 dt
0
Stąd:
T
1
⋅ ∫ i( t )2 dt
I=
T
(6.4)
0
Podobnie oblicza się wartości skuteczne innych wielkości charakteryzujących prąd
elektryczny. Na przykład wartość skuteczną napięcia wyznacza się z wzoru:
T
1
⋅ ∫ u( t )2 dt
U=
T
(6.4a)
0
Matematycznie wartość skuteczna jest więc pierwiastkiem ze średniej z wielkości
podnoszonej do kwadratu - po angielsku: „root mean square”. Pierwsze litery tego
anglojęzycznego terminu używane są w tym języku (a więc w międzynarodowym języku nauki i
techniki) jako stawiany przy jednostkach indeks oznaczający wartość skuteczną. Przykładowo
wartość skuteczną napięcia równą 230 V zapisuje się jako 230 Vrms.
Wartość skuteczna danej wielkości to wartość tej wielkości dla prądu stałego równoważna
jej skutkami energetycznymi, stąd wartości skuteczne oznacza się tak jak wielkości prądu stałego,
a więc dużymi literami (np.: I, U, V, E, J).
Jak to wynika z definicji, wartość skuteczna jest zawsze rzeczywistą liczbą dodatnią.
Dzieląc wartość maksymalną (amplitudę) przebiegu przez jego wartość skuteczną
otrzymuje się pewien współczynnik, który może być użyty do obliczania tej wartości
maksymalnej na podstawie znajomości wartości skutecznej. Jest to współczynnik szczytu:
W
(6.5a)
k sz = maks
Wsk
Definiuje się też współczynnik kształtu:
W
(6.5b)
k = sk
Wśr
Znajduje on zastosowanie przy skalowaniu mierników magnetoelektrycznych
wykorzystywanych do pomiarów wielkości sinusoidalnych. Mierzą one wartości średnie
przebiegów wyprostowanych, a wyskalowane są w wartościach skutecznych.
-5-
6.3. Moc czynna, moc pozorna, współczynnik mocy
Wartości chwilowe mocy z jaką energia jest pobierana lub wydawana przez dwójnik, równe
są iloczynowi wartości chwilowych natężenia prądu płynącego w dwójniku i napięcia
charakteryzującego pole elektryczne wymuszające ten prąd:
p = u ⋅i
(6.6)
Wynika to z definicji napięcia i natężenia (por. pkt. 1.4 rozdz. 1. pierwszej części
niniejszego skryptu: „Elektrotechnika Teoretyczna. Prąd stały.”).
Jeżeli przebiegi prądu i napięcia są zmienne w czasie to zmienny jest także przebieg mocy.
Jeżeli przebiegi te są okresowe, to również przebieg mocy jest okresowy (okres tego przebiegu na
ogół jest inny niż okresy napięcia i prądu). Można zatem wyznaczyć jego matematyczną wartość
średnią. Wartość tę nazwano mocą czynną. Oznacza się ją dużą literą „P” i wylicza z takiego
samego wzoru jak inne wartości średnie przebiegów okresowych:
T
P=
T
1
1
⋅ ∫ p( t )dt = ⋅ ∫ u( t ) ⋅ i( t )dt
T
T
0
(6.7)
0
Moc czynną można także definiować fizycznie jako taką nie zmieniającą się w czasie moc,
która w ciągu jednego okresu spowoduje przepływ energii równy przepływowi energii
rozważanego przebiegu okresowego.
Jednostką mocy czynnej jest wat ( 1[P ] = 1 W ).
Status mocy czynnej w elektrotechnice trafnie określa jej anglojęzyczna nazwa „true
power” - moc prawdziwa.
Iloczyn wartości skutecznych napięcia i prądu danego dwójnika elektrycznego nosi nazwę
mocy pozornej tego dwójnika. Oznacza się ją symbolem „ S ”:
(6.8)
S =U ⋅I
Pojęcia moc pozorna i moc czynna nie są stosowane w teorii obwodów prądu stałego. Dla
tych prądów moc pozorna jest równa mocy czynnej (i jest nazywana mocą, bez dodatkowych
dookreśleń). Inaczej jest w niektórych obwodach prądu zmiennego. Przesył energii z daną mocą
czynną (tj. daną mocą średnią) i przy danej wartości skutecznej napięcia, wymaga w tych
obwodach zastosowania natężenia prądu o większej wartości skutecznej niżby to było konieczne
gdyby moc czynna była równa mocy pozornej (i jak byłoby w obwodach prądu stałego).
Zazwyczaj dzieje się tak dlatego, że część energii dopływającej do odbiornika nie zamienia się w
nim na energię użyteczną, lecz jest tam magazynowana (w polach magnetycznych cewek i w
polach elektrycznych kondensatorów), a następnie zwracana do źródła. Oscyluje w ten sposób
bezproduktywnie pomiędzy odbiornikiem a źródłem, powodując zwiększenie wartości skutecznej
natężenia prądu.
Z tego powodu słuszna jest zależność:
(6.8)
S≥P
Moc pozorna nie jest zatem wielkością opisującą rzeczywistą moc z jaką energia przepływa
pomiędzy odbiornikiem a źródłem. Jest ona maksymalną wartością mocy średniej (mocy
czynnej), z jaka energia mogłaby przepływać, przy danych wartościach skutecznych napięcia i
prądu, gdyby w obwodzie nie zachodziło zjawisko oscylacji energii, lub inne zjawiska
pogarszające ten przepływ. Określa więc jedynie optymalne warunki odniesienia dla procesów
rzeczywiście zachodzących przy transferze energii.
Aby wyraźnie podkreślić, że moc pozorna nie jest rzeczywistą, „prawdziwą” mocą
fizyczną, nie mierzy się jej w watach. Jednostką mocy pozornej jest woltamper ( 1[S ] = 1VA ).
Stosunek mocy czynnej danego dwójnika do jego mocy pozornej nosi nazwę
współczynnika mocy:
-6-
T
λ=
P
P
=
=
S U ⋅I
1
⋅ u( t )i( t )dt
T ∫
0
T
T
0
0
(6.10)
1
1
⋅ ∫ i(2t )dt ⋅
⋅ ∫ u(2t )dt
T
T
Z definicji współczynnika mocy i z zależności (6.8.) wynika, że współczynnik ten może
przyjmować wartości z przedziału (domkniętego) 0,1 :
(6.10a)
0≤λ ≤1
Występowanie wartości współczynnika mocy mniejszej od jedności oznacza, że przepływ
energii odbywa się przy większych wartościach skutecznych prądu (lub napięcia) niż byłoby to
konieczne w warunkach optymalnych. Tak, jak gdyby źródło musiało generować jakąś dodatkową
energię transferowaną następnie do odbiornika, lecz nie zmieniającą się w energię użyteczną. Moc
z jaką przesyłana jest ta hipotetyczna dodatkowa energia nosi nazwę mocy biernej. Będzie ona
szczegółowiej omawiana w dalszych rozdziałach niniejszego podręcznika. W obwodach prądu
sinusoidalnie zmiennego tą nieużyteczną energią, występowanie której opisuje moc bierna, jest
energia rzeczywiście oscylująca pomiędzy odbiornikiem i źródłem. Jednak występowanie mocy
biernej może mieć za przyczynę także inne zjawiska fizyczne.
PRZYKŁAD
Rozważmy
obwód
rezystancyjny
z
wirującym łącznikiem o schemacie zastępczym
przedstawiony na rys. 6.4. Łącznik wiruje z
prędkością kątową ω = 2π / T , gdzie „T” to czas
jednego obrotu łącznika. Podczas każdego obrotu
obwód jest zamknięty jedynie przez czas „ τ ”. W
związku z tym, w obwodzie płynie prąd zmienny
okresowy, mimo iż zasilany jest on przez źródło
Rys. 6.4. Obwód rezystancyjny z wirującym łącznikiem
prądu stałego.
Należy wyznaczyć moce pozorną i czynną
źródła, a także jego współczynnik mocy.
Z opisu funkcjonowania łącznika wynika, że przebieg wartości chwilowych prądu
płynącego w obwodzie, w tym przez źródło, dla jednego okresu zmienności opisuje zależność:
 E
0 < t ≤τ

i( t ) =  Rs + Ro
 0
τ <t ≤T
2
τ

τ
1 
E
E

 dt =
⋅
Jego wartość skuteczna wynosi: I =
∫
T  Rs + Ro 
Rs + Ro T
0
Napięcie źródła:
Stąd jego wartość skuteczna:
Moc czynna źródła:
u źr ( t ) = e( t ) = E
U źr = E
τ
τ
0
0
τ
1
1
E
E2
⋅
Pźr = ⋅ ∫ u źr ( t ) ⋅ i( t ) dt = ⋅ ∫ E ⋅
dt =
T
T
Rs + Ro
Rs + Ro T
τ
E2
⋅
Rs + Ro T
Moc pozorna źródła:
S źr = E ⋅ I =
Współczynnik mocy:
P
τ
λ źr = źr =
, ( λ źr < 1 gdy τ < T )
S źr
T
-7-
Współczynnik mocy jest mniejszy od jedności, co wskazuje na fakt nieoptymalnego
wykorzystywania źródła. W obwodzie występuje zatem moc bierna. Jednak nie jest tu ona
związana z oscylacyjnym przepływem jakiejkolwiek energii. W tym wypadku nieoptymalność
polega na przerwach w przesyle energii. Właśnie dlatego natężenie prądu jest większe niż byłoby
to potrzebne do przesyłania energii z daną mocą czynną (mocą średnią) gdyby źródło było
wykorzystywane bez przerw (a więc optymalnie).
Z punktu widzenia źródła odbiornik jest rezystorem o zmiennej rezystancji (równej Ro lub
∞ ). Jak widzimy obciążenie źródła stałego takim odbiornikiem, a więc odbiornikiem
niestacjonarnym, daje efekt występowania mocy biernej.
Podobne rozważania przeprowadzone w odniesieniu do odbiornika (rezystora Ro ) dają
wynik Podb = S odb , z czego wynika, że współczynnik mocy ma tu wartość λ = 1 .
Gdy rozważać zjawiska energetyczne z punktu widzenia odbiornika, liniowy, stacjonarny
rezystor zasilany jest zmiennym napięciem o przebiegu prostokątnym. Moc bierna nie występuje.
Zatem powodem występowania mocy biernej w rozważanym przykładzie jest
niestacjonarność odbiornika.
6.4. Prąd sinusoidalnie zmienny
Na zaciskach wykonanej z materiału przewodzącego ramki, umieszczonej w polu
magnetycznym i wirującej z prędkością kątową „ω” (rys. 6.5a), skutkiem zjawiska indukcji
elektromagnetycznej, występuje napięcie (ściślej - pole elektryczne o napięciu) o przebiegu
czasowym pokazanym na rys. 6.5b.
Rys. 6.5. Napięcie sinusoidalnie zmienne a) powstawanie, b) przebieg w funkcji czasu
Przebieg ten opisuje wyrażenie matematyczne:
u( t ) = U m sin[ ω ( t + τ u )]
(6.11)
gdzie:
U m - to amplituda napięcia;
τ u - to czas jaki minął od chwili gdy napięcie miało wartość chwilową równą zero
(„przebieg przechodził przez zero”) do chwili kiedy rozpoczęto mierzenie czasu (chwili t = 0 ).
Zmienną niezależną jest tu czas (mierzony w jednostkach czasu, tj. w sekundach), zaś do
analitycznego zapisu musi zostać użyta funkcja trygonometryczna sinus (lub kosinus). Dziedziną
funkcji trygonometrycznych są kąty (mierzone w jednostkach miary kąta płaskiego, tj. w
radianach). Stąd zachodzi potrzeba przeliczania czasu na kąty - sekund na radiany. Stosowany tu
współczynnik przeliczeniowy nosi nazwę pulsacji (oznacza się go małą grecką literą „ ω ”). Jego
wartość wynika z zależności ω ⋅ T = 2π - okres funkcji sinus, równy „2π”, musi być równoważny
okresowi przebiegu czasowego „T”. Równoważność uzyskuje się za pomocą mnożenia przez
współczynnik przeliczeniowy.
-8-
Stąd wynika wzór na wyznaczanie pulsacji:
1
ω = 2π = 2πf
T
Jednostką pulsacji jest radian na sekundę ( 1[ω ] =
(6.12)
1[ < ]
rad
=1
).
1[ t ]
s
Konkretna wartość pulsacji danego
przebiegu sinusoidalnego wynika z prędkości
kątowej (też oznaczanej symbolem „ ω ” - por.
rys. 6.5a) z jaką kręci się wirnik prądnicy
generującej ten przebieg (Sprawa jest nieco
bardziej złożona, tak jest tylko wtedy gdy
pole magnetyczne prądnicy ma jedną parę
biegunów).
W elektrotechnice przyjęło się, że
przebiegi sinusoidalne przedstawiane są
Rys. 6.6. Napięcie sinusoidalne w funkcji kąta ωt
graficznie nie w funkcji czasu lecz w funkcji
iloczynu „ ωt ”, czyli odpowiadającego czasowi kąta - argumentu funkcji sinus (por. rys. 6.6). Kąt
ten nosi nazwę kąta fazowego. Zmienia się on w funkcji czasu - υ ( t ) = ωt +Ψ I . Nazwa pochodzi
stąd, że od wartości tego kąta zależy w jakiej fazie znajduje się w danej chwili czasowej przebieg
(czy jest to faza narastania, czy faza osiągania wartości maksymalnej, czy faza malenia, itd.).
Okresem tak przedstawianego przebiegu jest kąt pełny (2π), a zamiast czasu τu , jaki minął od
chwili gdy przebieg „przechodził przez zero” do chwili gdy rozpoczęto obserwację przebiegu (tj.
do chwili gdy t = 0 ), występuje odpowiadający temu czasowi kąt Ψ u = τ ⋅ ω , nazywany
początkowym kątem fazowym.
Rys. 6.7. Prąd sinusoidalnie zmienny, wyprostowany a) jednopołówkowo b) dwupołówkowo
Przebieg sinusoidalny (przykładowo - natężenia prądu) charakteryzują zatem następujące
parametry:
- amplituda:
- pulsacja:
I max , I m ;
ω = 2πf ;
2π
;
- okres:
T=
ω
1 ω
- częstotliwość:
;
f = =
T 2π
- kąt fazowy w funkcji czasu υ ( t ) = ωt +Ψ I ;
υ ( 0 ) = ω ⋅ 0 +Ψ I =Ψ I ;
- początkowy kąt fazowy:
I av = 0 ;
- wartość średnia:
-9-
Różna od zera jest wartość średnia przebiegu sinusoidalnego wyprostowanego
(jednopołówkowo i dwupołówkowo - por. rys. 6.7):
π
π
Im
I
1
1
⋅ ∫ I m sin( ωt )dωt =
⋅ ( − cos( ωt ) = m ⋅ [− ( −1 ) − ( −1 )] = I m
I av( j . p .) =
π
2π
2π
2π
0
(6.13a)
0
I av( d . p .) =
π
π
I
I
1
2
⋅ 2 ∫ I m sin( ωt )dωt = m ⋅ ( − cos( ωt ) = m ⋅ [− ( −1 ) − ( −1 )] = I m
π
π
π
2π
0
(6.13b)
0
- wartość skuteczna:
I=
1
⋅
2π
2π
2
2
∫ I m sin ( ωt )dωt = I m ⋅
0
1
⋅
2π
2π
∫ sin
0
2 ( ωt )dωt = I
m
I
1
⋅π = m
2π
2
(6.14)
Dla przebiegów sinusoidalnych słuszny jest więc wzór:
I
(6.14a)
I= m
2
(To NIE JEST definicja wartości skutecznej, a jedynie wzór na jej wyliczanie dla
przebiegów sinusoidalnych! - por. pkt 6.2)
W Europie napięcie znamionowe instalacji elektroenergetycznych niskiego napięcia ma
wartość skuteczną U = 230 V ( U = 230 Vrms ). Wartość maksymalna tego napięcia wynosi więc
U m = 2 ⋅ 230 V ≈ 325 V . Częstotliwość ma wartość f = 50 Hz . Odpowiada to okresowi
rad
1
= 0 ,02 s = 20 ms . Stąd wartość pulsacji - ω = 2π ⋅ 50 ≈ 314
.
T=
50
s
W Stanach Zjednoczonych i w niektórych innych krajach wartości te są następujące:
U = 110 Vrms , U m ≈ 155,6 V ,
f = 60 Hz ,
rad
.
T = 0 ,01( 6& ) s ≈ 16,7 ms , ω ≈ 377
s
Przebiegi sinusoidalne mające taką
samą pulsację (np. przebiegi natężenia prądu i
wymuszającego ten prąd napięcia) noszą
nazwę przebiegów synchronicznych.
Dla
przebiegów
synchronicznych
można wyznaczać przesunięcie fazowe
jednego przebiegu względem drugiego. Na
ogół oznacza się je małą grecką literą „ ϕ ”. W
Rys. 6.8. Dwa synchroniczne przebiegi sinusoidalne
przypadku przebiegów z rys. 6.8 wynosi ono:
ϕ =ΨU −Ψ I
(6.15)
Mówimy, że napięcie wyprzedza prąd o kąt „ ϕ ”, albo, że prąd opóźnia się o kąt „ ϕ ” w
stosunku do napięcia.
Suma przebiegów sinusoidalnych synchronicznych (o tej samej pulsacji) jest też
przebiegiem sinusoidalnym. Jej przebieg można wyznaczyć dodając do siebie wyrażenia
opisujące przebiegi składowe. Nie jest to jednak zbyt proste.
- 10 -
Niech prądy i1 i i2 z rys. 6.9. mają przebiegi:
i1( t ) = I1m sin( ωt + Ψ1 ) i i2 ( t ) = I 2m sin( ωt + Ψ2 ) . Prąd i3 jest ich
sumą: i3 = i1 + i2 .
Jego przebieg czasowy można wyznaczyć jako:
Rys. 6.9. Sumowanie prądów
i3 ( t ) = I1m sin( ωt + Ψ1 ) + I 2m sin( ωt + Ψ2 ) = I 3m sin( ωt + Ψ3 )
Wartości I 3m i Ψ3 można wyznaczyć wykorzystując
tożsamości trygonometryczne:
i3 ( t ) = I1m sin( ωt +Ψ1 ) + I 2m sin( ωt +Ψ 2 )
= I1m [sin( ωt ) cosΨ1 + cos( ωt ) sinΨ1 ] +
+ I 2m [sin( ωt ) cosΨ 2 + cos( ωt ) sinΨ 2 ] =
= sin( ωt )[ I 1m cosΨ 1 + I 2 m cosΨ 2 ]
+ cos( ωt )[ I 1m sinΨ 1 + I 2 m sinΨ 2 ] =
= sin( ωt )[ I 1m cosΨ 1 + I 2 m cosΨ 2 ]
+ cos( ωt )[ I 1m sinΨ 1 + I 2 m sinΨ 2 ]
To wyrażenie daje się przekształcać dalej, aż do postaci:
i3 (t) = ( I1m cosΨ1 + I 2m cosΨ 2 )2 + ( I1m sinΨ1 + I 2m sinΨ 2 )2 ⋅
I sinΨ1 + I 2m sinΨ 2
⋅ sin( ωt + ar tg 1m
)
1m cosΨ1 + I 2m cosΨ 2
Jak widać, obliczenia takie są pracochłonne nawet dla bardzo prostego przypadku. Właśnie
z tego powodu, już w XIX w. (pod jego koniec) elektrycy wymyślili metodę skutecznie je
upraszczającą. Jest nią metoda wskazów.
6.5. Metoda wskazów
Metoda wskazów odwołuje się do koła trygonometrycznego i do pojęcia wskazu
wirującego.
Rys. 6.9. Prąd sinusoidalny i wskaz wirujący wartości maksymalnej
Wskaz wirujący wartości maksymalnej jest rodzajem ruchomego (wirującego) wektora,
który odwzorowuje przebieg czasowy wielkości sinusoidalnie zmiennej. Na rys. 6.9. pokazano
przykładowo wskaz wartości maksymalnej natężenia prądu. Ma on długość równą amplitudzie
odwzorowywanego przebiegu, umieszczony jest w początku układu współrzędnych i obraca się w
kierunku przeciwnym do ruchu wskazówek zegara z prędkością kątową „ ω ”, równą pulsacji
przebiegu. Rzutując koniec takiego wektora na oś rzędnych („oś igreków”), można na niej
odczytywać wartości chwilowe natężenia prądu dla chwil „t”, odpowiadających kątom
„ ωt + ΨI ”. W chwili „t = 0”, a więc w umownej chwili rozpoczęcia pomiaru czasu, wskaz
nachylony jest w stosunku do osi odciętych („osi iksów”) pod kątem „ ΨI ”. Na tzw. wykresach
- 11 -
wskazowych, wykorzystywanych jako rodzaj graficznego odwzorowania przebiegów
sinusoidalnych, rysowany jest on właśnie w tym położeniu.
Takie odwzorowanie, dzięki swojej prostocie, przydatne jest przy porównywaniu wielu
przebiegów, zwłaszcza przy określaniu ich wzajemnych przesunięć fazowych. Jednak największą
zaletą tej metody przedstawiania przebiegów sinusoidalnych jest to, że dodane do siebie
geometrycznie wskazy dwu synchronicznych przebiegów sinusoidalnych dają wskaz przebiegu
sinusoidalnego będącego ich sumą. Pokazano to na rys. 6.10.
Rys. 6.10. Dodawanie prądów sinusoidalnych
jako wskazów wirujących wartości maksymalnej
Długość wskazu otrzymanego w wyniku geometrycznego dodawania wskazów składowych
jest równa amplitudzie tego sumarycznego przebiegu, kąt jaki ten wskaz tworzy z osią odciętych
(osią „iksów”) w chwili „t = 0” jest jego początkowym kątem fazowym.
Gdy wskaz ten obracać ze zwrotem przeciwnym do ruchu wskazówek zegara (jak na
rysunku), jego rzuty na oś rzędnych („oś igreków”), dla kolejnych kątów jaki wskaz tworzy z osią
odciętych („oś iksów”) odpowiadających kolejnym chwilom czasowym, dają wartości chwilowe
prądu i3 ( t )
W praktyce stosowane są nie wskazy wartości maksymalnych, a wskazy wartości
skutecznych. Różnią się one od wskazów wartości maksymalnych tym, że mają długość równą
2 razy krótsze od wskazów wartości
wartości skutecznej danej wielkości. Są zatem
maksymalnej, stąd uzyskane za ich pomocą wartości chwilowe przebiegów czasowych trzeba
przemnażać przez 2 .
PRZYKŁAD I:
Dane są dwa synchroniczne prądy sinusoidalne o natężeniach:
i1( t ) = 3 2 sin( 314t ) A i i 2( t ) = 5,657 cos(314t ) A
Należy wyznaczyć przebieg wartości chwilowych prądu będącego ich sumą:
i3 ( t ) = i1( t ) + i2 ( t )
Zastosujmy metodę wskazów wartości skutecznej:
Jest:
I
3 2
= 3 A , Ψ 1 = 0 rad ;
I 1 = 1 max =
2
2
π
i2( t ) = 5 ,657 cos( 314t ) A = 4 2 sin( 314t + ) A ;
2
I 2 max 5 ,657
π
=
= 4 A , Ψ 2 = rad ;
I2 =
2
2
2
Wskazy są nawzajem prostopadłe, do wyznaczania
długości będącego ich sumą wskazu warto więc zastosować
Rys. 6.11. Dodawanie wskazów prądu
twierdzenie Pitagorasa:
- 12 -
I 3 = I12 + I 22 = 3 2 + 4 2 = 5 A
Początkowy kąt fazowy Ψ3 można wyliczać stosując funkcje trygonometryczne:
I
4
Ψ3 = arc tg 2 = arc tg ≈ 0,927 rad (≈ 53,13o )
I1
3
Jest zatem:
i 3 ( t ) = I 3 2 sin(ωt + Ψ3 ) ≈ 5 2 sin(314 t + 0,927 ) ≈ 5 2 sin(314 t + 53,13o ) A
Kąt jaki się otrzyma mnożąc pulsację przez czas ma wartość wyrażoną w radianach jednostkach układu SI. Stąd kąt początkowego przesunięcia fazowego także powinien być
wyrażony w radianach (aby jedne dane wymiarami pasowały do drugich). Jednak podawane w
radianach wartości kątów nie są „intuicyjne” - wiemy „mniej więcej” jaki to jest kąt „ 53,13o ”,
mało kto ma podobne wyobrażenie o kącie „ 0,927 rad ”. Stąd elektrycy do określania wielkości
kątów stosują również stopnie (może nawet częściej od radianów).
PRZYKŁAD II:
Niech prądy i1( t ) i i2 ( t ) mają przebiegi:
π
i1( t ) = 3 2 sin( 314t + ) A
3
π
i i2 ( t ) = 5,657 sin( 314t + ) A
6
Należy wyznaczyć: i3 ( t ) = i1( t ) + i2 ( t )
Jest:
π
π
I1 = 3 A Ψ1 = rad i I 2 = 4 A
Ψ2 = rad
3
6
Tym razem wskazy reprezentujące prądy i1( t ) i
i2 ( t ) nie są wzajemnie prostopadłe, stąd obliczenia nie
będą już tak proste jak w poprzednim przykładzie. Do
wyznaczenia wartości I 3 i Ψ3 potrzebna jest znajomość
twierdzeń trygonometrycznych i - co ważniejsze - wymaga
to sporego nakładu pracy. Najprościej wylicza się te
parametry dodając do siebie rzuty wskazów na osie
odciętych i rzędnych. Takie rzuty nazywane są w
elektrotechnice
składowymi
ortogonalnymi
(prostopadłymi).
π
I1x = I1 cos Ψ1 = 3 ⋅ cos( ) = 1,5 A ,
3
π
I1 y = I1 sin Ψ1 = 3 ⋅ sin( ) ≈ 2,598 A
3
π
I 2 x = I 2 cos Ψ2 = 4 ⋅ cos( ) ≈ 3,464 A ,
6
π
I 2 y = I 2 sin Ψ2 = 4 ⋅ sin( ) = 2 A
6
Rys. 6.12a. Dodawanie wskazów prądu
I 3 x = I1x + I 2 x ≈ 1,5 + 3,464 = 4,964 A ,
I 3 y = I1 y + I 2 y ≈ 2 ,598 + 2 = 4,598 A
I 3 = I 32x + I 32y ≈ 4 ,964 2 + 4 ,598 2 ≈ 6 ,766 A
- 13 -
Rys. 6.12b. Dodawanie wskazów prądu metodą
dodawania ich składowych
I
4,964
Ψ 3 = arc tg 3x ≈ arc tg
≈ 0,747 rad ( ≈ 42,8 o )
I 3y
4,598
Jest zatem: i3 ( t ) ≈ 6 ,766 2 sin( 314t + 0 ,747 ) A
6.6. Metoda symboliczna
Metoda wykresów wskazowych ułatwia obliczanie przebiegów sinusoidalnych. Zamiast
dodawać funkcje czasu, co jest zajęciem dość skomplikowanym i pracochłonnym, dodaje się do
siebie (geometrycznie) reprezentujące je wskazy. Najprościej robi się to dodając do siebie rzuty
wskazów na osie układu współrzędnych, zwane ich składowymi ortogonalnymi.
Elektrycy znaleźli sposób, by jeszcze uprościć, „zautomatyzować” te obliczenia. Efekt ten
daje zastosowanie liczb zespolonych.
Reprezentacją liczby zespolonej Z = Z e jα = a + ib na płaszczyźnie liczb zespolonych jest
wektor o długości „Z” i o początku w początku układu współrzędnych, nachylony względem osi
liczb rzeczywistych pod kątem równym „ α ”. Dodawanie liczb zespolonych polega na dodawaniu
(geometrycznym) reprezentujących je wektorów.
Wszystko to idealnie pasuje do wskazów odwzorowujących przebiegi sinusoidalne. Można
je zatem utożsamiać z wektorami reprezentującymi liczby zespolone i nadawać im wartości
zespolone. Metoda, w której wskazy zapisuje się używając liczb zespolonych nosi nazwę metody
symbolicznej. Jej autorem był irlandzki uczony Arthur Edwin Kennelly (był synem oficera
pokładowego, sam przez krótki czas pracował jako elektryk okrętowy).
Stosując metodę symboliczną wskazowi wartości skutecznej odwzorowującemu przebieg
w( t ) (gdzie w( t ) to przebieg czasowy sinusoidalnego napięcia, natężenia, sem itd.), o długości
W
W = max i o kącie nachylenia względem osi odciętych (początkowym kącie fazowym
2
przebiegu) równym ΨW przyporządkowuje się liczbę zespoloną W ⋅ e jΨW o module W i
argumencie ΨW (reprezentuje ona wskaz, „symbolizuje go” - stąd nazwa metody). Wartość ta
nosi nazwę wartości skutecznej zespolonej. W efekcie takiego przyporządkowania,
geometryczne dodawanie wskazów wartości skutecznych zostaje zastąpione arytmetycznym
dodawaniem wartości skutecznych zespolonych.
W elektrotechnice, w odniesieniu do liczb zespolonych, zwyczajowo stosuje się nieco inne
oznaczenia niż w matematyce.
Przede wszystkim liczba urojona jest tu oznaczana literą „j”, a nie „i” - litera „i”
zarezerwowana jest dla oznaczania natężenia prądu.
Istnieją też trzy różne konwencje oznaczania wartości zespolonych wielkości
elektrycznych, przy czym dwie z nich występują „równolegle”. Rzadziej spotyka się i inne.
Tabela 6.1
konwencja
przestarzała, używana do połowy lat 1960-tych,
spotykana w starych podręcznikach
aktualna, spotykana w niektórych podręcznikach
(np. Cholewicki T.: Elektrotechnika teoretyczna.
WNT. 1973 i inne wyd..), a także w publikacjach
zagranicznych
aktualna, najpopularniejsza, ta którą będziemy
stosować
wartość zespolona
Î = I ⋅ e jΨ
symbol „z daszkiem”
I = I ⋅ e jΨ
bez wyróżniania
I = I ⋅ e jΨ
symbol podkreślony
- 14 -
moduł wartości zespolonej
I
bez wyróżniania
I
symbol wartości bezwzględnej
- na ogół niekonsekwentnie
I
bez wyróżniania
Niektóre kalkulatory wykonują działania na liczbach zespolonych. Pracujący w zawodzie
inżynier elektryk powinien mieć taki kalkulator. Powinien jednak także umieć radzić sobie i bez
niego.
W bardziej zaawansowanych rozważaniach teoretycznych, reprezentację sinusoidalnej
funkcji czasu poprzez wartość skuteczną zespoloną wyprowadza się przy pomocy tzw.
transformacji Fouriera. Zapoznamy się z nią w dalszym toku studiowania elektrotechniki
teoretycznej.
PRZYKŁAD III:
Wyznaczmy raz jeszcze prąd i3 ( t ) z poprzedniego przykładu. Tym razem zastosujmy
metodę symboliczną.
π
π
Jest:
i1( t ) = 3 2 sin( 314t + ) A i i2 ( t ) = 5,657 sin( 314t + ) A
3
6
Należy wyznaczyć: i3 ( t ) = i1( t ) + i2 ( t )
Przedstawmy przebiegi za pomocą ich wartości skutecznych zespolonych:
π
I1 = 3 A Ψ1 = rad
3
π
I 2 = 4 A Ψ 2 = rad
6
stąd:
π
I1 = 3 ⋅ e 3 A
stąd:
π
I2 = 4 ⋅ e 6 A
j
j
π
π
j
3
+ 4 ⋅ e 6 ≈ 4,9641 + j4,598 A
I 3 = I1 + I 2 = 3 ⋅ e
j
Aby można było wyznaczyć przebieg wartości chwilowych prądu i3 ( t ) trzeba
przekształcić I 3 z postaci algebraicznej do postaci wykładniczej:
I 3 ≈ 4,9641 + j4,598 ≈ 6 ,7664 ⋅ e j 0 ,747 A
Prąd i3 ( t ) ma przebieg: i3 ( t ) = 6 ,7664 2 sin( 314t + 0,747 ) A
6.7. Odbiornik liniowy, pasywny - impedancja, admitancja, prawo Ohma
Odbiornik liniowy, pasywny jest to taki odbiornik, który nie zawiera ani elementów o
charakterystykach nieliniowych, ani elementów źródłowych. Jeżeli do zacisków takiego
odbiornika przyłożyć napięcie sinusoidalne (ściślej - pole elektryczne o napięciu sinusoidalnie
zmiennym):
u( t ) = U 2 sin( ωt + ΨU )
to również płynący pod wpływem tego napięcia prąd jest prądem okresowym,
sinusoidalnym, o takiej samej pulsacji (a więc synchronicznym z napięciem):
i( t ) = I 2 sin( ωt + ΨI )
Rys. 6.13. Odbiornik liniowy, pasywny w obwodzie
prądu zmiennego
- 15 -
Rys. 6.14. Prąd i napięcie odbiornika liniowego,
pasywnego w obwodzie prądu zmiennego
Wartość skuteczna prądu jest przy tym wprost proporcjonalna do wartości skutecznej
napięcia:
U
I
(6.16a)
zaś przesunięcie fazowe miedzy prądem i napięciem jest (dla danego odbiornika) stałe i nie
zależy od wartości skutecznej napięcia:
ΨU −Ψ I = const = ϕ
(6.16b)
Dla wielkości nawzajem proporcjonalnych można wyznaczać współczynnik
proporcjonalności. Współczynnik proporcjonalności pomiędzy wartościami skutecznymi prądu i
U
nosi nazwę impedancji. Termin ten pochodzą od łacińskiego impedio napięcia Z =
I
przeszkadzam, tamuję, stoję na zawadzie.
Odbiornik pasywny, liniowy w obwodzie prądu zmiennego charakteryzują więc jego
impedancja „Z” i przesunięcie fazowe pomiędzy prądem i napięciem „ ϕ ”. Znając te wielkości
można na podstawie znajomości przebiegu prądu wyznaczyć wartość skuteczną wymuszającego
ten prąd napięcia, a także jego początkowy kąt fazowy:
U = Z ⋅ I
(6.17)

ΨU = Ψ I + ϕ
Zależności te stanowią prawo Ohma dla obwodów prądu sinusoidalnie zmiennego.
Jeżeli na podstawie znajomości przebiegu napięcia wyznaczony ma być prąd wygodniej jest
stosować inną postać prawa Ohma dla przebiegów sinusoidalnych:
I = Y ⋅ U
(6.18)

Ψ I = ΨU − ϕ
1 I
=
to
współczynnik
Z U
proporcjonalności, który nazwano admitancją.
I ta nazwa ma łaciński źródłosłów. Pochodzi od
czasownika admitto - dozwalam, przyjmuję.
Impedancja i admitancja, definiowane jako
współczynniki proporcjonalności pomiędzy napięciem i
prądem oraz prądem i napięciem, mają takie same
jednostki jak rezystancja i konduktancja, definiowane
identycznie, lecz dla obwodów prądu stałego:
[Z ] = 11V = 1Ω , [Y ] = 11A = 1S
1V
1A
Rys. 6.15. Odbiornik liniowy, pasywny - wykres
wskazowy napięcia i prądu
Sinusoidalnie zmienne napięcie i sinusoidalnie
zmienny prąd mogą być reprezentowane za pomocą
wskazów swoich wartości skutecznych. Wskazy te, narysowane w skali i umieszczone na jednym
rysunku, tworzą tzw. wykres wskazowy (rys. 6.15).
Wskazy można zapisać za pomocą liczb zespolonych, jako wartości skuteczne zespolone:
gdzie:
Y=
U = U ⋅ e jΨU
i I = I ⋅ e jΨ I
Jeżeli do wyrażenia na wartość skuteczną zespoloną napięcia podstawić zależności z prawa
Ohma (6.15) otrzymuje się:
U = U ⋅ e jΨU = Z ⋅ I ⋅ e j( ΨI + ϕ ) = Z ⋅ e jϕ ⋅ I ⋅ e jΨI
Wprowadzając oznaczenie Z = Z ⋅ e jϕ i uwzględniając, że I = I ⋅ e jΨI
wyrażenie na prawo Ohma w zapisie symbolicznym:
U = Z ⋅I
otrzymuje się
(6.19)
- 16 -
Wielkość Z = Z ⋅ e jϕ to impedancja zespolona. Jest ona współczynnikiem
proporcjonalności pomiędzy wartościami skutecznymi zespolonymi napięcia i prądu:
U
U
(6.20)
Z = = Z ⋅ e jϕ = ⋅ e j(ΨU −Ψ I )
I
I
Jej modułem jest impedancja, czyli współczynnik proporcjonalności pomiędzy wartościami
U
skutecznymi napięcia i prądu danego odbiornika ( Z = ), zaś argumentem - stałe (dla danego
I
odbiornika) przesunięcie fazowe pomiędzy przebiegami czasowymi napięcia i prądu
( ϕ =ΨU −Ψ I ). Impedancja zespolona opisuje właściwości odbiornika liniowego, pasywnego
jako elementu obwodu prądu sinusoidalnie zmiennego.
Równoważną („dualną”) postać prawa Ohma w zapisie symbolicznym otrzymuje się
wyznaczając napięcie na podstawie znajomości natężenia prądu:
I = I ⋅ e jΨI = Y ⋅ U ⋅ e j(ΨU − ϕ) = Ye − jϕ ⋅ Ue jΨU
Wprowadzając oznaczenie Y = Y ⋅ e − jϕ i uwzględniając, że U = U ⋅ e jΨU otrzymuje się
wyrażenie:
I = Y ⋅U
(6.21)
Wielkość Y = Y ⋅ e − jϕ to admitancja zespolona. Jest ona współczynnikiem
proporcjonalności pomiędzy wartościami skutecznymi zespolonymi prądu i napięcia:
I
I
(6.22)
Y = = Y ⋅ e − jϕ = ⋅ e j(Ψ I −ΨU )
U
U
Jej modułem jest admitancja - współczynnik proporcjonalności pomiędzy wartościami
I
skutecznymi prądu i napięcia występujących w danym odbiorniku - Y = , zaś argumentem stałe
U
przesunięcie fazowe pomiędzy przebiegami czasowymi prądu i napięcia - Ψ I −ΨU .
Admitancja zespolona jest odwrotnością impedancji zespolonej. Zatem zawiera te same co
tamta informacje o odbiorniku liniowym, pasywnym w obwodzie prądu sinusoidalnie zmiennego,
jedynie inaczej zapisane.
PRZYKŁAD
π
) A przy
6
napięciu o przebiegu u( t ) = 230 2 sin( 314t ) V . Do odbiornika tego przyłożono napięcie o
π
przebiegu czasowym u' ( t ) = 24 2 sin( 314t + ) V . Należy wyznaczyć przebieg prądu przy tym
3
nowym napięciu, a także wskazania woltomierza i amperomierza mierzącego napięcie i natężenie
prądu.
Wartości skuteczne zespolone napięcia i prądu wynoszą:
Rozważmy odbiornik, którego prąd ma przebieg czasowy i( t ) = 5 2 cos( 314t +
2
j π
j
0
U = 230 ⋅ e = 230 V oraz I = 5 ⋅ e 3 A
Admitancja zespolona odbiornika ma więc wartość:
2
j π
5⋅e 3
2
j π
I
Y= =
≈ 0 ,02174 ⋅ e 3 S
230
U
Nowe napięcie ma wartość skuteczną zespoloną:
π
j
U ' = 24 ⋅ e 6 V
- 17 -
Wartość skuteczną zespoloną nowego prądu można wyliczyć jako:
2
5
π
j π
j
j π
I' = Y ⋅ U ' ≈ 0 ,02174 ⋅ e 3 ⋅ 24 ⋅ e 6 = 0 ,52 ⋅ e 6 A
Tak więc wartość skuteczna prądu wynosi I' ≈ 0 ,52176 A ;
5
Jego początkowy kąt fazowy ma wartość Ψ I' = π
6
Stąd nowy prąd ma następujący przebieg wartości chwilowych:
5
5
i' ( t ) ≈ 0 ,52 ⋅ 2 sin( 314t + π ) ≈ 0,164 ⋅ sin( 314t + π ) A
6
6
Woltomierz i amperomierz mierzą wartości skuteczne odpowiednio napięcia i prądu, zatem
ich wskazania wynoszą: UV = 24 V i I A ≅ 0 ,52 A
- 18 -