Fizyka 8

Zagadnienia
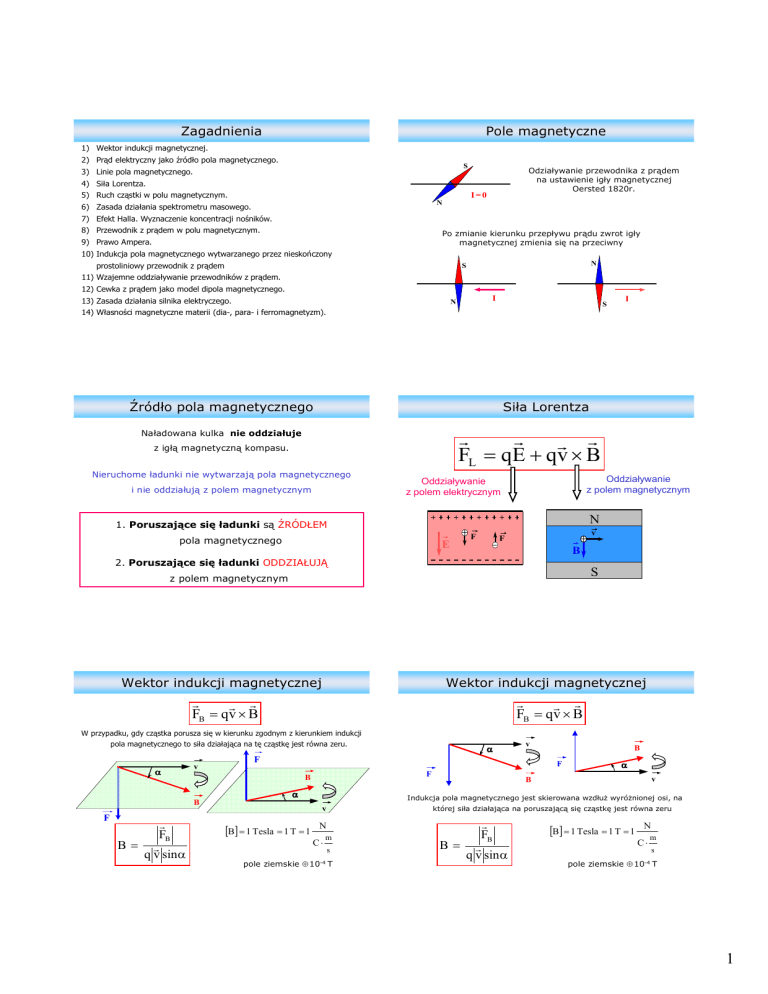
Pole magnetyczne
1) Wektor indukcji magnetycznej.
2) Prąd elektryczny jako źródło pola magnetycznego.
S
3) Linie pola magnetycznego.
Odziaływanie przewodnika z prądem
na ustawienie igły magnetycznej
Oersted 1820r.
4) Siła Lorentza.
I=0
5) Ruch cząstki w polu magnetycznym.
N
6) Zasada działania spektrometru masowego.
7) Efekt Halla. Wyznaczenie koncentracji nośników.
8) Przewodnik z prądem w polu magnetycznym.
Po zmianie kierunku przepływu prądu zwrot igły
magnetycznej zmienia się na przeciwny
9) Prawo Ampera.
10) Indukcja pola magnetycznego wytwarzanego przez nieskończony
prostoliniowy przewodnik z prądem
N
S
11) Wzajemne oddziaływanie przewodników z prądem.
12) Cewka z prądem jako model dipola magnetycznego.
13) Zasada działania silnika elektryczego.
I
N
S
I
14) Własności magnetyczne materii (dia-, para- i ferromagnetyzm).
Źródło pola magnetycznego
Siła Lorentza
Naładowana kulka nie oddziałuje
r
r
r r
FL = qE + qv × B
z igłą magnetyczną kompasu.
Nieruchome ładunki nie wytwarzają pola magnetycznego
i nie oddziałują z polem magnetycznym
Oddziaływanie
z polem magnetycznym
Oddziaływanie
z polem elektrycznym
N
N
1. Poruszające się ładunki są ŹRÓDŁEM
pola magnetycznego
E
F
v
F
B
2. Poruszające się ładunki ODDZIAŁUJĄ
S
z polem magnetycznym
Wektor indukcji magnetycznej
Wektor indukcji magnetycznej
r
r r
FB = qv × B
r
r r
FB = qv × B
W przypadku, gdy cząstka porusza się w kierunku zgodnym z kierunkiem indukcji
pola magnetycznego to siła działająca na tę cząstkę jest równa zeru.
α
v
F
r
FB
B= r
q v sin α
v
B
F
F
B
B
α
F
α
v
B
Indukcja pola magnetycznego jest skierowana wzdłuŜ wyróŜnionej osi, na
v
[B] = 1 Tesla = 1 T = 1
α
której siła działająca na poruszającą się cząstkę jest równa zeru
N
C⋅
m
s
pole ziemskie ≈ 10-4 T
r
FB
B= r
q v sin α
[B] = 1 Tesla = 1 T = 1
N
C⋅
m
s
pole ziemskie ≈ 10-4 T
1
Linie pola magnetycznego
Linie pola magnetycznego
1. Krzywe, do których styczne w kaŜdym punkcie pokrywają się z
kierunkiem wektora indukcji pola magnetycznego
2. Liczba linii na jednostkę powierzchni mierzona w płaszczyźnie
prostopadłej do linii jest proporcjonalna do wartości wektora indukcji
pola magnetycznego
I
I
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
I
Linie pola magnetycznego są zawsze liniami
zamkniętymi, obejmującymi przewodnik z prądem
Ze względu na analogię między polami magnetycznymi
magnesów trwałych i solenoidów Ampere (1821-22)
sformułował hipotezę o uwarunkowaniu właściwości
magnesów trwałych występującymi w nich mikroprądami.
Pola skrzyŜowane
Zadanie 1
Uszereguj przedstawione cztery
Wiązka
elektronów
działającej na poruszającą się,
B
E
v2
B
przypadki pod względem wartości siły
v3
E
naładowaną dodatnio cząstkę, przy
załoŜeniu, Ŝe cząstka znajduje się w
v1
obszarze jednorodnego pola
r r
v⊥B
kierunki pokazano na rysunku.
FE
evB sin 90 o = eE
⇒
v=
1
FE
v1
FB=0
Fd = ma = m
r r
v⊥B
4
FE
FE
V3
V4
FB=0
FB
Cząstka w polu magnetycznym
B
v
FB
vp = ve ⇒
2
v
r
FB
rp
re
v = ωr =
o
T=
FB
FB
rp
v
FB
v2
evB sin 90 = m
r
v
eB = m
r
B
mv
eB
r=
v
mv
r=
eB
3
FE
V2
FB
E
B
FB
2
v
Poruszająca się cząstka w polu magnetycznym
r
r r
FB = qv × B
r
r
FB = Fd
v4
elektrycznego i magnetycznego, których
r
r
FB = − FE
v
me
2π
r
T
2 πm 1
=
eB
ν
Tp
Te
=
mp
=
≈ 1840
F
neutron
v
v
F
v
mp
me
re
v
2
Spektrometr masowy
Ruch cząstki po torze śrubowym
Pole elektryczne dostarcza naładowanej
cząstce energii, która jest przekształcana
w energię kinetyczną:
Tor ruchu cząstki, która porusza się
w polu magnetycznym z prędkością
tworzącą kąt α z wektorem indukcji
tego pola
α vII
v
v⊥
B
r
d
T=
d=
v
2qU
m
v=
U
+
v
-
W komorze cząstka porusza się w jednorodnym
polu magnetycznym o indukcji B po półokręgu
o promieniu r i uderza w płytę światłoczułą w
odległości x od punktu wejścia do komory:
2 πm
eB
2πmv cos α
eB
x = 2r = 2
Zjawisko Halla
mv 2 2mU
=
qB B
q
Ź
m B2 x 2
=
q
8U
stąd
Wyznaczenie koncentracji nośników
r
r
FB = −FE
B
B
I
Powstawanie
r
cząstka wpada więc do komory z prędkością:
d = Tv II = Tv cos α
B
B
mv 2
= qU
2
I
evB sin 90 o = eE
dodatkowego
I
pola
elektrycznego
VA
(róŜnicy
F
v
VB
VA
F
vB = E
VB
potencjałów)
vB =
v
w umieszczonym
VA
w polu
FB
FE
VB − VA U
=
d
d
j
v=
ne
E=
U
d
VB
v
magnetycznym
n=
przewodniku,
przez który
jBd IBd
=
eU eUS
S = hd
przepływa prąd
VA > VB
VA < VB
Oddziaływanie pola magnetycznego na
przewodnik z prądem
FB = qv d B sin 90 o
n=
h
Doświadczenie to moŜe być wykorzystane do wyznaczenia znaku większościowych
nośników prądu (znak nośników decyduje o kierunku polaryzacji płytki)
d
Moment siły działający na ramkę z prądem
I=0
F2
r r r r r
τ = r1 × F1 + r2 × F2
B
B
r r r r
r1 × F1 = r2 × F2
B
I
q = It = I
r
r
v d II L
L
FB
vd
L
vd
FB = ILB
r
r r
FB = IL× B
I
FB
S
r r
r
τ = 2 r1 × F1
r1
N
r2
I
I
I
b
τ = 2 FB sin α = b IaB
{ sin α
2
F
B
b
F1
τ = IBS sin α
FB
BI
Uhe
r r
r
τ = I S× B
r1
a
3
Zasada działania silnika
Dipol magnetyczny
Para sił działająca na
pętlę wytwarza
moment sił i powoduje
obrót ramki
Najbardziej podstawową strukturę magnetyczną stanowi dipol magnetyczny.
Elektron poruszający się po orbicie kołowej moŜna traktować jako prąd płynący w pętli.
Pętla z prą
prądem jako model
dipola magnetycznego
r r
µ = IS
µ
oddziaływanie pola
magnetycznego na
przewodnik z
prądem
Pętla z prądem
umieszczona w polu
magnetycznym
doświadcza
oddziaływania dwóch
przeciwnie
skierowanych sił
B
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
r r
r
τ = I S× B
r r r
τ = µ×B
magnetyczny
moment dipolowy
S
W praktyce silniki posiadają
wiele uzwojeń, co zapewnia
bardziej jednolite warunki
obrotu. Pole magnetyczne
jest wytwarzane przez
elektromagnes
Moment sił
sił dział
działają
ający
na ramkę
ramkę umieszczoną
umieszczoną
w polu magnetycznym
F
I
F
r
τ = µB sin Θ
Moment sił
sił ma wartość
wartość maksymalną
maksymalną, gdy
moment magnetyczny jest prostopadł
prostopadły do
kierunku pola magnetycznego, natomiast
dla Θ=0o lub Θ= 180o jest ró
równy zero.
Zadanie
Prawo Ampera
Elektron poruszają
poruszający się
się po orbicie koł
kołowej moŜ
moŜna traktować
traktować jako prą
prąd pł
płyną
ynący w
pętli. Oblicz orbitalny moment magnetyczny elektronu przy tym zał
załoŜeniu.Wyraź
eniu.Wyraź
orbitalny moment magnetyczny za pomocą
pomocą orbitalnego momentu pę
pędu.
KrąŜenie wektora indukcji magnetycznej wzdłuŜ dowolnej
r r
µ = IS
µ orb =
krzywej otaczającej prąd jest równe iloczynowi natęŜenia
tego prądu i przenikalności magnetycznej próŜni
e
πr 2
2π r / υ
µ orb
eυr
=
2
L = r ×p
I
L = mυr sin 90
µ orb =
υ
L
e
mυr
2m
∆l i
∑ B ⋅ ∆l
i
i
po krzywej zamkn .
Bi
I
µ
o
i
= µo I
przenikalność
magnetyczna
próŜni
∆li→0
r
e r
µ orb = −
L
2m
Zadanie 2
Prąd płynący w przewodniku
wytwarza wirowe pole
magnetyczne.
∫ B ⋅ dl = µ I
o
Prawo to stosowane jest do obliczeń indukcji pola
magnetycznego w pewnych szczególnych przypadkach
Nieskończony, prostoliniowy przewodnik jako źródło pola
magnetycznego
Obliczyć krąŜenie wektora indukcji po krzywych 1, 2 i 3
∫ B ⋅ dl = µ I
dl
1)
3
∫ B ⋅ dl = −µ o I1
r
I2
2
o
B
2)
I3
∫ B ⋅ dl = µ
o
(− I1 + I 3 )
∫ B cos0
o
dl = µ o I
B ∫ dl = µ o I
I
I1
B2 πr = µ o I
1
3)
∫ B ⋅ dl = µ
o
(I 2 + I 3 )
B=
µoI
2 πr
4
Siły działające między dwoma przewodnikami z prądem
r
r r
F12 = I 2 L 2 × B1
1
I1
Oddziaływanie dwóch przewodników z prądem
r
r
L 2 ⊥ B1
d
F12 = I 2 L 2 B1
B1 =
2
F12
I2
F12 =
B1
I1 F
21
F12 I2
I2
I1
F21
F12
µ o I1
2 πd
µo
I1I 2 L 2
2 πd
1 Amper oznacza natęŜenie prądu stałego, który płynąc w
dwóch równoległych, prostoliniowych, nieskończonych
przewodach wywołuje siłę oddziaływania o wartości 2—10-7 N na
kaŜdy metr długości przewodu
F21
B2
B1
F12
B2
B1
F21
F12
Przewody w których płyną
prądy w kierunkach przeciwnych
odpychają się
Przewody w których płyną
prądy w kierunkach zgodnych
przyciągają się
Podstawowe typy materiałów magnetycznych
Diamagnetyzm
diamagnetyki
Do diamagnetykó
diamagnetyków zalicza się
się: gazy szlachetne, prawie wszystkie metale i
Samorzutnie nie wykazują właściwości magnetycznych. Po umieszczeniu
w zewnętrznym polu magnetycznym powstaje w nich pole magnetyczne, skierowane
przeciwnie do pola zewnętrznego. Diamagnetyk jest wypychany z obszaru pola
magnetycznego (odpychanie przez magnes, zjawisko lewitacji).
paramagnetyki
Posiadają trwałe dipolowe momenty magnetyczne, które zmieniają swoją
orientację przestrzenną pod wpływem zewnętrznego pola magnetycznego z
chaotycznej na częściowo uporządkowaną. Proces porządkowania jest zakłócany
przez drgania termiczne. Wewnętrzne pole magnetyczne skierowane jest zgodnie z
zewnętrznym polem magnetycznym.
ferromagnetyki
Grupy dipoli magnetycznych, ukierunkowanych równolegle, tworzą obszary
spontanicznego namagnesowania, zwane domenami magnetycznymi. W
nieobecności pola momenty magnetyczne wszystkich, bezładnie zorientowanych
domen znoszą się, dając zerowy bądź zbliŜony do zera wypadkowy moment
magnetyczny całego ciała.
Zastosowanie zewnętrznego pola magnetycznego powoduje uporządkowanie domen
– wewnątrz ciała ferromagnetycznego powstaje pole o kierunku zgodnym z
kierunkiem pola zewnętrznego, które moŜe setki, nawet tysiące razy przewyŜszać
przyłoŜone pole zewnętrzne
metaloidy nie wykazują
wykazujące wł
własnoś
asności parapara- lub ferromagnetycznych (np
(np::
bizmut, krzem, cynk, magnez, zł
złoto, miedź
miedź) a takŜ
takŜe fosfor, grafit, woda oraz
wiele zwią
związkó
zków chemicznych. Diamagetyczne są teŜ
teŜ DNA i wiele biał
białek.
Diamagnetyki nie wykazują
wykazują samorzutnie
właściwoś
ciwości magnetycznych.
Pole magnetyczne diamagnetyka jest
skierowane przeciwnie do pola zewnę
zewnętrznego.
trznego.
Diamagnetyk jest wypychany z obszaru pola
magnetycznego (odpychanie przez magnes,
zjawisko lewitacji).
B=0
B
http://www.hfml.sci.kun.nl/levitation-movies.html
Diamagnetyk w polu magnetycznym
Diamagnetyk w nieobecności pola magnetycznego
v
FE
FE
v
v
B=0
r
ωo
ωo
FB
v
r
r
µ orb = − 2em L
r
FB FE
FE
ωo-∆
∆ω
I
µ
L
I
Brak namagnesowania dla B=0.
Atomy nie mają
mają wypadkowego momentu magnetycznego
(tyle samo elektronó
y w kaŜ
elektronów krąŜ
krąŜy
kaŜdym z kierunkó
kierunków)
NiezaleŜ
NiezaleŜnie od kierunku ruchu elektronu
wytwarza się
się dodatkowo indukowany
magnetyczny moment dipolowy ∆µ
skierowany przeciwnie do kierunku pola
magnetycznego o wartoś
wartości:
∆µ = 12 er∆ω
ωo+∆
∆ω
-µ
µ+∆
∆µ
µ
L
lewitująca Ŝaba ( Bo= 16 T)
Nijmegen High Field Magnet Laboratory
ω − ωo = ∆ω = 2eB
m
B
I
∆µ = 12 er 2 ∆ω =
I
µ+∆
∆µ
B = 2T
∆µ =
(1.6 ⋅10
e2r 2B
4m
C ) (5.3 ⋅10 −11 m ) 2T
= 4 ⋅10 −29 A ⋅ m 2
4 ⋅ 9.1 ⋅10 −31 kg
−19
2
2
5
Paramagnetyzm
Paramagnetyzm
Właściwoś
ciwości paramagnetyczne posiadają
posiadają substancje o niesparowanych
elektronach. Ich atomy obdarzone są niezerowym momentem magnetycznym
(np. cyna, platyna).
platyna).
Trwał
Trwałe dipole magnetyczne paramagnetyka pod wpł
wpływem zewnę
zewnętrznego pola
magnetycznego zmieniają
zmieniają swoją
swoją orientację
orientację przestrzenną
przestrzenną z chaotycznej na
częś
ciowo uporzą
częściowo
uporządkowaną
dkowaną (dąŜą
(dąŜą do ustawienia zgodnego z kierunkiem
zewnę
zewnętrznego pola magnetycznego). Wewnę
Wewnętrzne pole magnetyczne
skierowane jest zgodnie z zewnę
zewnętrznym polem magnetycznym.
magnetycznym.
Proces porzą
porządkowania jest zakł
zakłócany przez drgania termiczne. Paramagnetyk
jest przycią
przyciągany przez magnes,
magnes, jednak znacznie sł
słabiej niŜ
niŜ ferromagnetyk.
ferromagnetyk.
B
r
Magnetyzacja
(namagnesowanie) to
moment magnetyczny
jednostki objętości próbki
M=
∑µ
i
i
V
Maksymalna wartość
wartość
wypadkowego momentu magnetycznego pró
próbki:
Mmax=Nµ
=Nµ
N - liczba wszystkich momentó
momentów magnetycznych pró
próbki
Prawo Curie
M=C
Bo
T
Magnetyczne własności materii
• Wzrost indukcji pola magnetycznego B
prowadzi do wzrostu uporządkowania
dipoli magnetycznych
Dla materiałów diamagnetycznych i paramagnetycznych indukowane pole magnetyczne
(o indukcji magnetycznej Bind) jest proporcjonalne do przyłoŜonego zewnętrznego pola
o indukcji Bo. Wypadkowa indukcja magnetyczna B jest sumą Bo i Bind
• Wzrastająca temperatura T
przeciwdziała porządkowaniu
Bind
67
8
B = B o + χ M Bo
stała
Krzywa namagnesowania dla siarczanu chromowo-potasowego. Zakres
liniowy, w którym spełnione jest prawo Curie: Bo/T < 0.5 [T/K]
1
przenikalność
magnetyczna ośrodka
B = µ Bo
0,5
M/Mmax
zakres temperatur
1÷4K
diamagnetyki
paramagnetyki
ferromagnetyki
0
0
1
2
3
podatność
magnetyczna
µ = 1 + χM
µ
<1
>1
>> 1
χM
<0
>0
>> 1
4
Bo/T [T/K]
Podatność magnetyczna χM
Diamagnetyki
Paramagnetyki
ołów
-1.5⋅⋅10-6
cyna
2⋅⋅10-6
woda
- 8.8 ⋅10-6
aluminium
13⋅⋅10-6
miedź
- 9 ⋅10-6
magnez
15⋅⋅10-6
złoto
- 34 ⋅10-6
chrom
315⋅⋅10-6
bizmut
- 176 ⋅10-6
mangan
1021⋅⋅10-6
Ferromagnetyki
Istnieje wiele krystalicznych przedstawicieli ferromagnetyków: Ŝelazo, kobalt,
nikiel oraz w niŜszych temperaturach równieŜ gadolin, terb, dysproz, holm i erb
wśród pierwiastków oraz wiele stopów i związków chemicznych.
Charakterystyczną cechą ferromagnetyków jest występowanie uporządkowania
magnetycznego w makroskopowych obszarach zwanych domenami.
Utrzymanie domen magnetycznych, czyli wytworzenie pola magnetycznego w
duŜym obszarze, jest stanem charakteryzującym się bardzo duŜą energią.
ObniŜenie energii kryształu w nieobecności pola magnetycznego realizowane
jest poprzez zmianę namagnesowania tak, by magnetyczne momenty dipolowe
utworzonych domen równowaŜyły się wzajemnie, a pole magnetyczne na
zewnątrz ciała było jak najmniejsze.
Zastosowanie zewnętrznego pola magnetycznego powoduje uporządkowanie
domen – wewnątrz ciała ferromagnetycznego powstaje pole o kierunku
zgodnym z kierunkiem pola zewnętrznego, które moŜe setki, nawet tysiące razy
przewyŜszać przyłoŜone pole zewnętrzne
B
W przypadku ferromagnetyków wartość χM>>1 (a takŜe µ>>1) i zaleŜy od Bo.
6
Histereza magnetyczna ferromagnetyków
ZaleŜność namagnesowania od indukcji pola magnetycznego
Nasycenie
http://pl.wikipedia.org/wiki/Histereza#Histereza_magnetyczna
Magnetyzacja
Materiał
nienamagnesowany
Indukcja zewnętrznego
pola magnetycznego
Wraz ze wzrostem indukcji zewnętrznego pola
magnetycznego wzrasta namagnesowanie próbki, aŜ
do momentu osiągnięcia stanu nasycenia, gdy
kryształ jest jednorodnie namagnesowany (wszystkie
dipole są ustawione równolegle)
ZaleŜność pola indukowanego (BM) od pola
zewnętrznego (B0) jest nieliniowa dla
ferromagnetyków, a więc wartość χM (a
takŜe µ) zaleŜy od B0.
Wraz ze wzrostem natęŜenia pola magnetycznego Bo
wzrasta namagnesowania (wzrost BM), które w punkcie
b osiąga stan nasycenia. Pomimo zmniejszenia Bo do
zera utrzymuje się stan namagnesowania. Dopiero po
przyłoŜeniu przeciwnie skierowanego pola Bk (tzw. pole
koercji) namagnesowanie znika całkowicie.
Bk
Rodzina pętli histerezy B=f(H) dla orientowanej blachy elektrotechnicznej,
na wykresie zaznaczono pozostałość magnetyczną BR oraz koercję HC.
DuŜa wartość
pozostałości
magnetycznej
Nasycenie
Prawo Curie -Weissa
Mała powierzchnia
pętli histerezy oznacza
niewielką wartość
energii rozproszonej
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Materiały magnetycznie
półtwarde - zapis
informacji komputerowych
(twarde dyski, dyskietki,
taśmy magnetyczne, karty
kredytowe)
Materiały
magnetycznie
miękkie – poŜądana
minimalizacja energii
rozproszonej w
transformatorach,
silnikach
W zaleŜności od materiału kierunek namagnesowania oraz granice domen mogą
zmieniać się łatwo (ferromagnetyki miękkie) lub trudno (ferromagnetyki twarde).
Materiały
magnetycznie
twarde
(magnesy trwałe)
W odpowiednio wysokiej temperaturze intensywne
drgania sieci krystalicznej ferromagnetyka powodują
rozpad domen na pojedyncze momenty magnetyczne
i ferromagnetyk staje się paramagnetykiem.
Temperatura, w której zachodzi to zjawisko, nazywa
się temperaturą Curie i np. dla Ŝelaza wynosi
TC=1043° K. a namagnesowanie powyŜej TC jest
opisane przez prawo Curie-Weissa:
M=C
B
T − TC
STRUMIEŃ INDUKCJI POLA MAGNETYCZNEGO
Prawo Gaussa dla pól magnetycznych
jest równy iloczynowi
r
r skalarnemu indukcji pola
magnetycznego B i wektora powierzchni S
Linie indukcji magnetycznej magnesu wychodzą z bieguna północnego,
a wchodzą do południowego. Są zawsze liniami zamkniętymi.
Jest to konsekwencja faktu iŜ nie istnieją w przyrodzie
odizolowane monopole magnetyczne - dzieląc magnes trwały na
części nie moŜna oddzielić jego biegunów.
Dla pola jednorodnego (B = const,
linie pola są równoległe)
S
r r
Φ = B⋅S
Φ = B S cosΘ
Θ
Wartość strumienia indukcji pola magnetycznego
przechodzącego przez dowolną zamkniętą
powierzchnię jest równa zero
∑ B ⋅ ∆S
B
i
Dla pola niejednorodnego
Φ=
∑B
i
i
⋅ ∆ Si
∆S
B
Fig.
a
Fig.
b
I
i
=0
i
∆Si→0
∫ B ⋅ dS = 0
7
Doświadczenie Faradaya
Reguła Lenza
NatęŜenie prądu płynącego
w pierwszym zwoju wzrasta
Iind
Iind
Iind
S
N
I1↑
Prąd indukowany płynie w takim
kierunku, Ŝe strumień pola
magnetycznego wytworzonego przez
ten prąd przeciwdziała zmianie
strumienia magnetycznego, który
ten prąd indukuje
S
N
I1↓
Iind
G
G
G
1. Prąd płynie gdy pętla i magnes poruszają się względem siebie
I1=const
2. Szybszy ruch wytwarza prąd o większym natęŜeniu
G
3. PrzybliŜanie bieguna północnego magnesu indukuje prąd w
kierunku przeciwnym niŜ w przypadku jego oddalania
Prawo indukcji Faradaya
Sposoby wzbudzania SEM
Wartość SEM indukowanej w obwodzie równa
jest szybkości, z jaką strumień indukcji
magnetycznej przechodzący przez ten
obwód zmienia się w czasie
ε
dΦ B
=−
dt
ΦB =
ε
r r
∫ B ⋅ dS
S
ε = − N dΦdt
Dla cewki o N zwojach
⇓
ε=0
1. Zmiana wartości indukcji pola magnetycznego w cewce
(zmiana połoŜenia magnesu względem cewki, zmiana
natęŜenia prądu w cewce - samoindukcja lub w sąsiednim
obwodzie – indukcja wzajemna)
2. Zmiana powierzchni cewki (powiększanie rozmiarów cewki
lub przesuwanie jej względem obszaru, gdzie istnieje pole)
B
3. Zmiana kąta pomiędzy wektorem indukcji magnetycznej
i wektorem powierzchni (obracanie cewki)
Zasada działania prądnicy prądu przemiennego
I
ν
Φ B = const
d
= − ∫ BdS cosΘ
dt S
[Φ
ΦB]=1 Wb=1T—1m2
Matematyczny zapis
reguły Lenza
B
NatęŜenie prądu płynącego
w pierwszym zwoju maleje
Iind=0
R
ε = − dΦdt
Prądnica prądu przemiennego
Θ=0
Φ = max
B
ε =0
Θ = π/2
Φ=0
Φ B = B a b cosΘ
b
a
Zmiana kąta miedzy wektorem indukcji
magnetycznej i wektorem powierzchni
powoduje wytworzenie SEM
Θ = ωt =2πνt
ε = max
Φ B = Bab cos(2 πνt )
Θ
B↑
S
ε = −Bab dtd (cos 2πνt )
ε = Bab
πν sin (2 πνt )
1
4224
3
ε
ε =ε
0
o
sin (2 πνt )
ε
Φ
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Φ B = Φ max cos (2 πνt )
ε = ε sin (2πνt )
o
0
1
2
3
4
5
6
7
8
ϕ [rad]
-2
8