euroelektra

„EUROELEKTRA”
OLIMPIADA ELEKTRYCZNA I ELEKTRONICZNA
Rok szkolny 2006/2007 - Etap drugi - Grupa elektroniczna
Rozwiązania zadań
Zadanie 1
Zaprojektować realizację translatora 4-bitowego, naturalnego kodu binarnego (kod binarny prosty) na kod
Gray’a, z minimalną ilością użytych, prostych bramek logicznych.
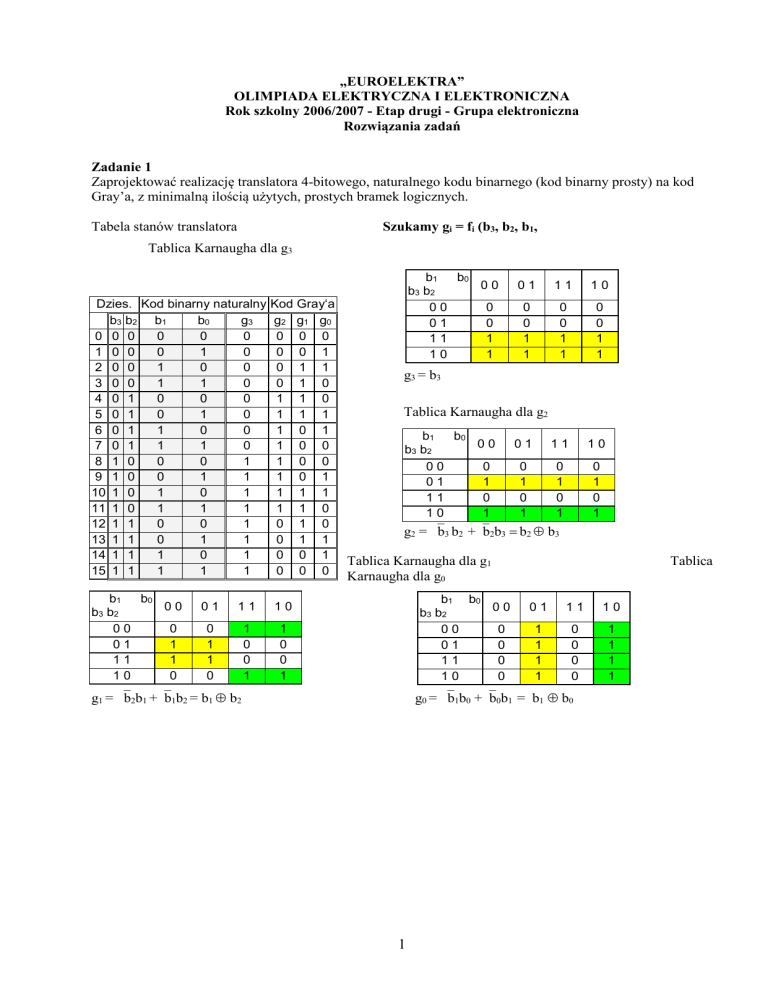
Tabela stanów translatora
Szukamy gi = fi (b3, b2, b1,
Tablica Karnaugha dla g3
Dzies. Kod binarny naturalny
b3 b2 b1
b0
g3
0 0 0
0
0
0
1 0 0
0
1
0
2 0 0
1
0
0
3 0 0
1
1
0
4 0 1
0
0
0
5 0 1
0
1
0
6 0 1
1
0
0
7 0 1
1
1
0
8 1 0
0
0
1
9 1 0
0
1
1
10 1 0
1
0
1
11 1 0
1
1
1
12 1 1
0
0
1
13 1 1
0
1
1
14 1 1
1
0
1
15 1 1
1
1
1
b1
b0
00
b3 b2
00
0
01
1
11
1
10
0
b1
b0
00
b3 b2
00
0
01
0
11
1
10
1
01
11
Kod Gray‘a
0
0
g2 g1 g0
0
0
0 0 0
1
1
0 0 1
1
1
0 1 1
g3 = b3
0 1 0
1 1 0
Tablica Karnaugha dla g2
1 1 1
1 0 1
b1
b0
00 01 11
1 0 0
b3 b2
1 0 0
00
0
0
0
1 0 1
01
1
1
1
1 1 1
11
0
0
0
1 1 0
10
1
1
1
0 1 0
g2 = b3 b2 +b2b3 b2 b3
0 1 1
0 0 1
Tablica Karnaugha dla g1
0 0 0 Karnaugha dla g
10
0
0
1
1
10
0
1
0
1
Tablica
0
01
11
10
0
1
1
0
1
0
0
1
1
0
0
1
b1 b0
00
b3 b2
00
0
01
0
11
0
10
0
g1 = b2b1 +b1b2 = b1 b2

01
11
10
1
1
1
1
0
0
0
0
1
1
1
1
g0 = b1b0 +b0b1 = b1 b0

1
UCY 7486 (3/4)
G3
1
3
G2
2
7486
4
6
G1
5
7486
9
8
G0
10
B3
B2
B1
B0
7486
Zadanie 2
Narysować przebiegi na wyjściach A, B, C, D, gdy na wejściu Set jest jedynka logiczna. Jaką rolę pełni
pokazany układ? Na wejście „wej” podawane są impulsy prostokątne.
1
1
1
1
c)
SET
J
A
Q
K
Q
K
CLR
B
SET
J
SET
Q
J
Q
K
CLR
Q
SET
C
J
Q
Q
K
CLR
D
Q
CLR
Wej
Przebiegi czasowe
wej
QA
QB
QC
QD
Jest to licznik asynchroniczny modulo 10, zliczający w kodzie binarnym naturalnym (BCD) do przodu.
Graf układu jest następujący
0  1  2  3  4  5  6  7  8  9  0  1
itd.
Zad. 3.
Przyjąć, że dla obu tranzystorów =100 (współczynnik wzmocnienia prądowego w konfiguracji ze
wspólnym emiterem) oraz, że UBE = 0,6 V i nie zależy od prądu emitera. Obliczyć napięcie UO na wyjściu
układu pokazanego na rysunku.
Dane:
UCC
UCC = 5 V
UCC
UBE = 0,6 V
R3 IB2
IB2
RT
R1
= 100
T2
T2
IC1
R1 = 300 k
IB1
IE2
IE2
R2 = 1 k
T1
R3 = 3 k
UT
UO
UO
R4 = 50 
R4
R4
R2
2

Rys. A
Rys. B
Z punktu widzenia tranzystora T2, część układu z rys. A położona po jego lewej stronie (na lewo od linii
przerywanej) może być zastąpiona źródłem Thevenina, co prowadzi do schematu pokazanego na rys. B.
Parametry UT i RT źródła Thevenina można wyznaczyć w oparciu o schemat z rys. A. Stosując prawa
Kirchoffa i prawo Ohma można napisać równanie:
U CC  I B1 R1  U BE  I B1 (1   ) R2 ,
z którego wynika wartość prądu bazy tranzystora T1:
I B1 
U CC  U BE
 1,1mA
R1  R2 (1   )
Napięcie UT jest napięciem na kolektorze T1 względem masy gdy IB2 = 0 (odłączony tranzystor T2) i wynosi:
UT  U CC  I C1 R3  1,7V
Rezystancja RT źródła Thevenina (przy pomięciu rezystancji kolektor-emiter tranzystora T1) jest równa:
RT  R3  3k
Znając wartości UT i RT można w oparciu o schemat z rys. B obliczyć IB2, a następnie UO. Prąd IB2 przyjmuje
wartość:
I B2 
U T  U BE
 0,1375 mA ,
RT  R4 (1   )
natomiast szukane napięcie UO wartość:
U O  I B2 (1   ) R4  687 ,5mV
Zad. 4
W układzie pokazanym na rysunku, służącym do obniżania poziomu napięcia stałego, idealne przełączniki S1
oraz S2 są przełączane naprzemiennie, tzn. gdy S1 jest zwarty, S2 jest rozwarty i na odwrót. Czas trwania
stanu zwarcia S1 (rozwarcie S2) w każdym cyklu przełączania wynosi tON, a cały cykl (załączenie i
wyłączenie S1) trwa TS (okres sygnału sterującego przełączaniem). Elementy R, L, C tworzą filtr
dolnoprzepustowy. Przyjmując, że stała czasowa RC tego filtru jest znacznie większa od TS wyznaczyć i
narysować napięcie wyjściowe Uwy jako funkcję stosunku tON/TS (współczynnik wypełnienia sygnału
sterującego) dla stałej wartości napięcia Uwe.
S1
L
U1
C
R
Uwy
S2
Uwe
Rys. A
Napięcie na wejściu filtru, oznaczone przez U1, jest wynikiem cyklicznego przełączania kluczy S1 i S2 i ma
przebieg czasowy pokazany na rys. B.
U1
Uwe
Uśr
0
t
tON
TS
Rys. B.
Można łatwo pokazać, że transmitancja napięciowa filtru RLC z rys. A, zdefiniowana jako T=Uwyj/U1, ma
charakter dolnoprzepustowy. Dla bardzo dużej wartości stałej czasowej filtru można przyjąć, że spełniona
jest także nierówność:
LC  TS
3
Przy spełnieniu tego warunku filtr tłumi składowe zmienne i przenosi na wyjście tylko składową stałą
napięcia U1, tj. tylko wartość średnią tego napięcia.
Z rys. B widać, że wartość średnia napięcia U1 jest opisana wzorem:
U śr 
t
1 TS
U1dt  U we ON ,

TS 0
TS
Ostatecznie daje to liniową zależność Uwy od stosunku tON/TS w postaci:
t
U wy  U śr  U we ON ,
TS
co zilustrowano graficznie na rysunku poniżej.
Uwy
Uwe
tON/TS
0
1
Zad. 5
W pokazanym układzie źródła napięć stałych U1, U2 oraz UDD są tak dobrane, że prąd stały płynący przez
kanały obu tranzystorów jest równy ID = 1mA. Obliczyć wzmocnienie napięciowe na obu wyjściach, tzn. A1
= uO1/ui oraz A2 = uO2/ui, dla sygnałów sinusoidalnie zmiennych małej częstotliwości. Przyjąć, że prąd drenu
każdego z tranzystorów jest związany z jego napięciem bramka-źródło zależnością ID =K(VGS -VP)2,
UDD
R = 2,4 k
gdzie:
K = 2,5x10-2 A/V,
VP = 1 V .
uO2
T2
U2
uO1
T1
ui
ID
U1
Z zależności:
I D  K VGS  VP 2
wynika wzór na transkonduktancję tranzystora polowego:
gm 
I D
 2 K VGS  V P   2 K I D
VGS
Dla podanych w treści zadania wartości ID = 1mA oraz K = 2,5x10-2 A/V daje to wartość:
g m1  g m2  5mS ,
identyczną dla obu tranzystorów T1 i T2.
Wzmocnienie napięciowe stopnia wzmacniającego zbudowanego z tranzystora MOS pracującego w
konfiguracji ze wspólnym źródłem i obciążonego rezystorem R opisane jest ogólnym wzorem:
AV  g m R
W przypadku pierwszego wyjścia (napięcie uO1) obciążeniem R jest rezystancja wejściowa drugiego stopnia,
tj. rezystancja widziana ze źródła tranzystora T2. Rezystancja ta jest równa:
Ri 2 
1
g m2
 0,2k ,
co daje wzmocnienie napięciowe równe:
u
A1  O1  g m1 Ri 2  1
ui
4
Prąd drenu obu tranzystorów jest identyczny (zarówno prąd stały, jak i zmienny). Oznacza to, że
transkonduktancja zdefiniowana jako pochodna prądu ID tranzystora T2 po napięciu UGS tranzystora T1 jest
równa transkonduktancji gm1. Uwzględniając fakt, że obciążeniem tranzystora T2 jest rezystor R=2,4kdaje
to następujące wzmocnienie napięciowe na wyjściu drugim:
u
A2  O 2  g m1 R  12
ui
Zad. 6
Dla idealnego wzmacniacza operacyjnego charakterystyka przejściowa układu pokazanego na rys. A ma
przebieg pokazany na rys. B. Wykorzystując dodatkowy wzmacniacz operacyjny i rezystory rozbuduj układ
z rys. A tak, by uzyskać charakterystykę przejściową pokazaną na rys. C.
R
D2
Uwy
R
D1
Uwe
R
Uwy
Uwe
Rys. A.
Rys. B
Uwy
Uwe
Rys. C
Napięcia na katodzie diody D2 i na anodzie diody D1 są w przeciwfazie. By uzyskać pożądaną
charakterystykę wystarczy zastosować rozważany układ uzupełniony o sumator, który będzie odejmował
od napięcia na anodzie diody D1 napięcie na katodzie diody D2. Funkcję tę realizuje układ pokazany na
rys.1.
5
R
D2
R
R
R
R
D1
Uwy
R
Uwe
Rys.1.
6
R