Uploaded by
common.user4509
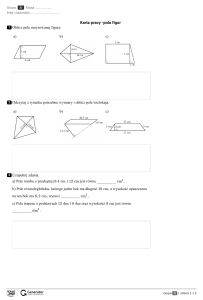
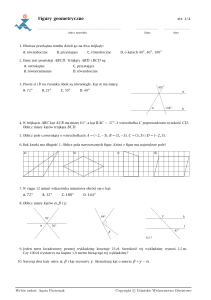
Klasówka z geometrii: czworokąty, pola, obwody
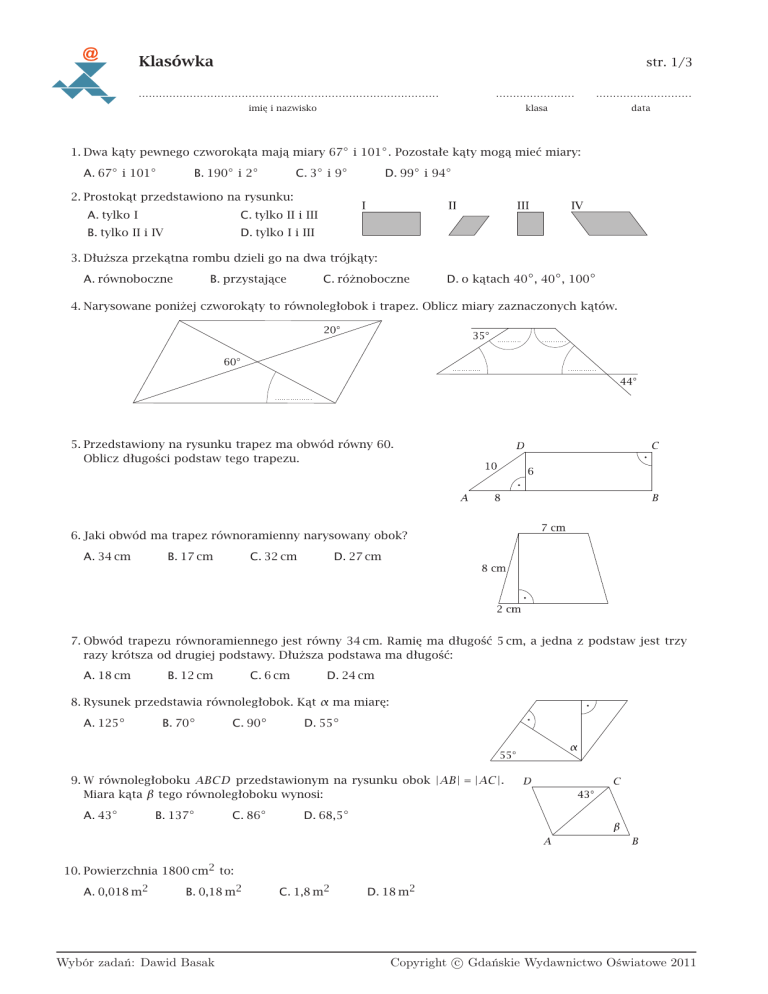
Klasówka str. 1/3 ....................................................................................... ....................... imię i nazwisko ............................ klasa data 1. Dwa kąty pewnego czworokąta mają miary 67◦ i 101◦ . Pozostałe kąty mogą mieć miary: A. 67◦ i 101◦ B. 190◦ i 2◦ C. 3◦ i 9◦ D. 99◦ i 94◦ 2. Prostokąt przedstawiono na rysunku: A. tylko I C. tylko II i III B. tylko II i IV D. tylko I i III 3. Dłuższa przekątna rombu dzieli go na dwa trójkąty: A. równoboczne B. przystające C. różnoboczne D. o kątach 40◦, 40◦, 100◦ 4. Narysowane poniżej czworokąty to równoległobok i trapez. Oblicz miary zaznaczonych kątów. 5. Przedstawiony na rysunku trapez ma obwód równy 60. Oblicz długości podstaw tego trapezu. 6. Jaki obwód ma trapez równoramienny narysowany obok? A. 34 cm B. 17 cm C. 32 cm D. 27 cm 7. Obwód trapezu równoramiennego jest równy 34 cm. Ramię ma długość 5 cm, a jedna z podstaw jest trzy razy krótsza od drugiej podstawy. Dłuższa podstawa ma długość: A. 18 cm B. 12 cm C. 6 cm D. 24 cm 8. Rysunek przedstawia równoległobok. Kąt α ma miarę: A. 125◦ B. 70◦ C. 90◦ D. 55◦ 9. W równoległoboku ABCD przedstawionym na rysunku obok |AB| = |AC|. Miara kąta β tego równoległoboku wynosi: A. 43◦ B. 137◦ C. 86◦ D. 68,5◦ 10. Powierzchnia 1800 cm2 to: A. 0,018 m2 B. 0,18 m2 Wybór zadań: Dawid Basak C. 1,8 m2 D. 18 m2 Copyright c Gdańskie Wydawnictwo Oświatowe 2011 str. 2/3 a 11. 25 000 m2 to: A. 2,5 ha B. 25 ha C. 25 a D. 2500 a 12. Prostokąt o wymiarach 0,7 m na 12 cm ma pole równe: A. 8,4 m2 B. 8,4 cm2 C. 0,084 m2 D. 84 cm2 13. Bok kwadratu o polu 81 dm2 ma długość: A. 9 cm B. 90 m C. 81 cm D. 9 dm 14. Która z podanych powierzchni jest największa? A. 0,9 ha B. 1 km2 C. 800 a D. 8000 m2 15. Jeden metr kwadratowy pewnej wykładziny kosztuje 23 zł. Szerokość tej wykładziny wynosi 2,5 m. Czy 100 zł wystarczy na kupno 1,9 metra bieżącego tej wykładziny? 16. Jeden bok prostokąta jest o 4 cm dłuższy od drugiego. Obwód tego prostokąta wynosi 4 dm. Oblicz jego pole. 17. Pan Jan planuje wyłożyć ścianę w przedpokoju panelami o wymiarach 250 cm × 15 cm. Jedno opakowanie zawiera 10 takich paneli. Ile opakowań paneli powinien kupić, jeśli ściana ma kształt prostokąta o wymiarach 2,5 m × 4 m? 18. Oblicz pole czworokąta o wierzchołkach A = (−4, −2), B = (2, −2), C = (2, 4) i D = (−4, 4). 19. Pole trójkąta ABC, gdzie A = (−3, 4), B = (3, 4) i C = (0, 6) jest równe: A. 18 B. 6 C. 12 D. 24 20. Pole trapezu przedstawionego na rysunku obok możemy obliczyć, korzystając ze wzoru: A. (p + t)·u 2 B. (a +2b)·h C. 1 2 (r + p) · t D. r +p 2 ·u 21. Pole trójkąta przedstawionego na rysunku jest równe: A. 8 B. 16 C. 28 D. 14 22. Oblicz pola i obwody narysowanych wielokątów. a) równoległobok Wybór zadań: Dawid Basak b) trapez równoramienny Copyright c Gdańskie Wydawnictwo Oświatowe 2011 str. 3/3 a 23. Bok kratki ma długość 1. Oblicz pola narysowanych figur. Która z figur ma największe pole? 24. Dłuższa podstawa trapezu ma 10 cm, wysokość trapezu jest równa 8 cm, a pole wynosi 56 cm2 . Jaką długość ma krótsza podstawa trapezu? A. 7 cm B. 4 cm C. 3,2 cm D. 8 cm 25. Pole rombu jest równe 24 cm2 . Krótsza przekątna ma 6 cm, a dłuższa ma długość: A. 16 cm B. 4 cm C. 12 cm D. 8 cm 26. Oblicz pole figury przedstawionej na rysunku. 27. Jaką część równoległoboku ABCD stanowi trójkąt AED? 13 A. 20 B. 5 8 7 C. 10 7 D. 20 28. W trapezie równoramiennym każde z ramion ma 13 cm, a wysokość 5 cm. Obwód trapezu jest równy 70 cm. Oblicz pole trapezu. 29. Oblicz pola figur: a) b) c) 30. Całą powierzchnię działki w kształcie trapezu o wymiarach przedstawionych na rysunku należy obsiać trawą. Ile opakowań nasion trawy trzeba kupić, jeżeli jedno opakowanie wystarcza na obsianie 2 m2 powierzchni? Wybór zadań: Dawid Basak Copyright c Gdańskie Wydawnictwo Oświatowe 2011