w postaci sinusoidalnego napięcia

Elektrotechnika elektronika miernictwo
Franciszek Gołek ([email protected])
www.pe.ifd.uni.wroc.pl
Wykład 3.
Obwody prądu sinusoidalnego
(Omówimy jak powstają sinusoidalne wymuszenia,
jak analizujemy obwody prądu zmiennego z pomocą
liczb i funkcji zespolonych)
Obecnie powszechnie dostępna energia elektryczna jest
produkowana w postaci sinusoidalnego napięcia
wymuszającego sinusoidalne natężenie prądu
elektrycznego.
Częstotliwość tego zmiennego (mówimy też
przemiennego) napięcia wynosi 50 Hz w Europie lub 60
Hz w Ameryce północnej.
Dzięki transformatorom łatwo można zmieniać wielkość
amplitud napięć i prądów zmiennych.
Energia elektryczna (= Usk•Isk•t) w postaci dużych
zmiennych napięć przy małych natężeniach prądów jest
łatwa do ekonomicznego transportu przy użyciu sieci linii
transmisyjnych krajowego systemu energetycznego.
Wszędzie gdzie pożądane jest napięcie stałe stosowane
są układy konwersji nazywane prostownikami.
Generowanie napięć zmiennych w elektrowniach polega
na zamianie innych rodzajów energii na energię
elektryczną z wykorzystaniem prawa Faradaya ∇×E =
-dB/dt czyli SEM = - dΦ/dt (jedno z równań Maxwella).
Dostępną energię (wiatrową, wodną, jądrową czy
cieplną) wykorzystuje się do wirowania odpowiednimi
zwojnicami w silnym polu magnetycznym.
Idea źródła napięcia sinusoidalnego:
Uzwojenie w postaci ramki wiruje ze stałą
prędkością kątową ω w stałym polu
magnetycznym o indukcji B. Końce ramki
połączone są z pierścieniami, które ocierają się
(ślizgają) o dociskane sprężynowo szczotki.
Oznaczając przez „A” pole powierzchni
obejmowanej ramką możemy określić
zależność czasową strumienia Φ
przenikającego ramkę jako: Φ = B·A·cos(ωt).
Generowana siła elektromotoryczna (SEM) e
-dΦ/dt = ωBAsin(ωt) = Emaxsin(ωt)
=
W elektrotechnice podstawowym przebiegiem napięć i prądów (wymuszeń i
skutków) jest przebieg sinusoidalny. Takie przebiegi są generowane przez
wirujące maszyny elektryczne zwane generatorami prądu zmiennego. Z
podstaw trygonometrii wiadomo, że przebieg sinusoidalny można otrzymać
przez rzutowanie promienia koła trygonometrycznego, wirującego ze stałą
prędkością kątową ω na nieruchomą oś. Wynik rzutowania na oś y jest
identyczny z rzutowaniem na oś x, ale przesunięty w czasie.
Liczby zespolone
Dysponując tylko liczbami rzeczywistymi mamy problem z
rozwiązaniem takich równań jak np.:
X2 + 1 = 0.
Jeżeli jednak za X podstawimy coś co nie jest liczbą rzeczywistą:
√-1, to podnosząc do kwadratu tę dziwną wielkość otrzymujemy
liczbę rzeczywistą -1. Zatem to coś spełnia równanie:
X2 + 1 = 0. Podobnie możemy podstawić za X wartość -√-1.
Jeżeli uznamy wielkość „√-1” za coś „realnego” i oznaczymy przez
„j” to z łatwością rozwiążemy wiele innych równań, przykładowo
równanie X2 + 9 = 0 spełniają rozwiązania: X = - 3j oraz +3j.
W elektronice stosujemy symbol: j = √-1 = (-1)0.5, chociaż
w matematyce używany jest symbol i = (-1)0.5.
Powód: bo „i” w elektronice to prąd elektryczny.
Liczby i funkcje zespolone w elektrotechnice i elektronice.
Liczby zespolone mają postać dwuskładnikową (zespoloną): Z = x
+ jy. Gdzie j = √-1 jest pierwiastkiem kwadratowym z liczby -1.
Taka notacja przypomina zapis położenia punktu na płaszczyźnie
przy pomocy dwóch (równoprawnych) współrzędnych: Z = (x, y).
W dziedzinie liczb zespolonych jest jednak pewna asymetria np.
kwadrat liczby czysto rzeczywistej (x + j0) jest wielkością czysto
rzeczywistą dodatnią (x2 + j0) a kwadrat liczby czysto urojonej (0 +
jy) jest wielkością czysto rzeczywistą ujemną (-y2 + j0) bo j2 = -1.
Dlatego liczby zespolone traktujemy jako zapis położenia punktu
na płaszczyźnie zespolonej. Wielkości zespolone (liczby i funkcje)
są wyjątkowo udaną abstrakcją stosowaną w opisie oscylacyjnych
przebiegów napięć i prądów w elektryczności oraz elektronice.
Dobrym tego przykładem są tzw. wykresy wskazowe, które
zastosujemy przy analizie układów RLC zasilanych napięciami
sinusoidalnymi. Zapis przebiegów sinusoidalnych w
postaci funkcji zespolonych jest niezastąpiony przy
analizie zależności amplitudowych i fazowych.
Przypomnijmy równość Eulera:
ejx = cos(x) + jsin(x)
oraz równoważność formuł:
Aej(ωt + φ) = Acos(ωt + φ) + jAsin(ωt + φ)
z obrazem punktu wirującego na płaszczyźnie
zespolonej z prędkością kątową ω - zwaną też
pulsacją.
Równość Eulera po raz pierwszy pojawiła się w 1714 roku w
postaci:
Przy pomocy rozwinięć w szereg potęgowy można pokazać:
Mnożenie wielkości zespolonych jest łatwe
gdy zastosujemy postać wykładniczą!
Przykładowo zapis prawa Ohma jako iloczynu zespolonego prądu I i tzw.
zawady Z (Z to zespolona - uogólniona oporność, jak zobaczymy niebawem):
U = I · Z = Iej(ωt + α) · Zejβ = ZIej(ωt + α+ β) = Uej(ωt + θ)
Mamy tu doskonałą ilustruję relacji amplitudowej i fazowej:
amplitudowa: U = IZ
i faz początkowych: α oraz θ
=α+β
Faza wyniku mnożenia to suma faz czynników!
Zapis zespolony ilustruje też zależności faz od czasu:
faza U = argument U = ωt + α + β = ωt + θ.
Zilustrujmy iloczyn z poprzedniej strony:
U = I × Z = Iej(ωt + α) × Zejβ = ZIej(ωt + α+ β) = Uej(ωt + θ)
Przy pomocy obrazów:
W iloczynie mamy sumę argumentów i iloczyn modułów.
Zatem dowolną wielkość np. napięcie u = Umcos(ωt + ϕ) o amplitudzie A = Umax
możemy rozumieć jako część rzeczywistą napięcia zapisanego w postaci
zespolonej U = Umaxej(ωt + ϕ). Ze względu na zmienną t – czas, dobrą ilustracją
może być animacja/film pokazująca jak z upływem czasu wektor U wiruje bo
rośnie jego argument, czyli kąt między nim a osią odciętych: ωt + ϕ.
Przy analizie i obliczeniach
wybieramy jednak sytuację
„zatrzymaną w kadrze” czyli
wybieramy jakąś dogodną
chwilę np. t = 0. Dla wybranej
dowolną wielkość zespoloną
A możemy i będziemy
zapisywać na 4 równoważne
sposoby:
http://faraday.ee.emu.edu.tr/EENG224/lecture_notes.htm
http://staff.southwest.tn.edu/kfoster/links_4.htm
Zajmiemy się teraz pojemnością i indukcyjnością,
które znane są między innymi z tego, że napięcia i
prądy w nich występujące nie są zgodne w fazie.
Początek ładowania kondensatora to duży prąd i małe
napięcie, a koniec to zero prądu i maksymalne napięcie!
Tu prąd jest potrzebny do zmian napięcia.
W cewce aby „rozpędzić” prąd zaczynamy
od dużego napięcia i powoli rosnącego prądu. Gdy prąd
osiągnie maksimum i przestaje się zmieniać mamy
zerowe napięcie. Tu napięcie jest potrzebne do zmian
natężenia prądu.
Kondensatory w obwodach elektronicznych (podobnie
jak oporniki i cewki) są elementami biernymi, nie mogą wzmacniać czyli
zwiększać moc sygnału elektrycznego. Kondensator jest dwójnikiem (dwa
zaciski) i składa się z dwóch okładzin przewodzących o dużej powierzchni
odizolowanych dielektrykiem o dużej przenikalności elektrycznej.
Kondensatory realizują koncepcję magazynowania energii w postaci pola
elektrycznego między naładowanymi elektrycznie okładkami. Ich efektywność
zależy od powierzchni i kształtu okładek, od odstępu oraz materiału między
okładkami. Żywotność zależy od takich parametrów pracy jak:
przykładane napięcia czy temperatura. Stosowane konstrukcje i
materiały są rozmaite i nadal ulepszane. Kondensatory, podobnie jak rezystory
należą do grupy podstawowych elementów elektroniki.
Schemat
zastępczy
Uwagi o odczycie parametrów kondensatorów
Kondensatory o dużych pojemnościach (podobnie jak rezystory dużej mocy) są na tyle
duże, że na ich obudowie wystarcza miejsca na napisanie wartości pojemności razem z
jednostkami. Przykład: kondensatory elektrolityczne.
Napis: +500MF oznacza, że końcówka bliższa znaku + musi mieć potencjał nie niższy
od potencjału drugiej końcówki (w przeciwnym wypadku kondensator ulegnie
zniszczeniu), pojemność kondensatora wynosi 500 µF. Znak - oznacza końcówkę, dla
której przewidziany jest niższy potencjał. Kondensatory o mniejszych rozmiarach to np.
kondensatory tantalowe. Napis +4R7µ oznacza 4.7µF (R oznacza miejsce dziesiętne).
Taki sam kondensator może być oznaczony napisem: +475k, k oznacz tu tolerancję
(±10%) natomiast cyfry 475 oznaczają 47×10 do potęgi 5 pF. Jednostki należy
odgadnąć na podstawie następujących wskazówek.
1) Przeważnie stosujemy mikro i pikofarady a unikamy mili- i nano-faradów,
największe wśród typowych pojemności to około 500 μF i znaczne rozmiary
kondensatora. Przykładowo napis: “680” musi zatem oznaczać 680 pF.
2) Pikofarad jest bardzo małą wartością i zwykle spotykamy kondensatory o
pojemności większej od 1 pF. Oznacza to, że znajdując napis: “.01” należy go
odczytać jako 0.01µF. Zatem wcześniejszy napis: “475” oznacza 4.7×105pF.
Przykładowo napis “.02M 1kV” oznacza 0.02 mikrofaradów, “M” – oznacza tu
tolerancję 20%, a “1kV” oznacza, że kondensator wytrzymuje naładowanie do napięcia
1000V.
Napis: “560M 1kV” oznacza 560pF o tolerancji 20% i napięcie 1kV.
Napis: “101k 200V” oznacza 100pF i kondensator na 200V.
Kody tolerancji: Z - +80%,-20%, M - ±20%, K - ±10%, J - ±5%, G - ±2%, F - ±1%, D ±0.5%, C - ±0.25%, B - ±0.1%, A - ±0.05%, N - ±0.02%.
Spotykamy i stosujemy kondensatory o różnej budowie. Np. kondensatory
Mylarowe (mailarowe) występują w postaci długich, zwiniętych folii metalowych
oddzielonych folią z mylaru. Znak paska oznacza końcówkę folii zewnętrznej.
Kondensatory te nie nadają się do pracy w układach wysokiej częstotliwości, gdyż długie
zwinięte folie stanowią zbyt dużą indukcyjność dla napięć w. cz.. Kondensatory
ceramiczne wyglądają jak płaskie kostki lub dyski (“lizaki”) i w przeciwieństwie do
kondensatorów mylarowych dobrze pracują w układach wysokiej częstotliwości.
Kondensatory ferroelektryczne: tanie i o dużej pojemności, są nieprecyzyjne i
stosowane do odsprzęgania i filtracji. Ogólnie produkowane są kondensatory o
pojemnościach od 0,1pF do około 5F w szeregach E6 i E12.
Największe dostępne obecnie pojemności to kondensatory UltraCap do 3000F.
Ładunek i napięcie na idealnym kondensatorze
spełniają następujący związek:
Q = CU.
Różniczkując obie strony „po czasie”
otrzymujemy
dQ/dt = CdU/dt.
dQ/dt jest oczywiście prądem ładowania I.
Z równości I = CdU/dt widać, że stały prąd (ładowania)
oznacza stałe tempo zmian napięcia na kondensatorze.
Prąd jest wprost proporcjonalny nie do napięcia, jak dla
opornika, lecz do szybkości zmian napięcia!
Brak proporcjonalności między wartościami
chwilowymi napięcia i prądu wyklucza zastosowanie
prawa Ohma w dziedzinie liczb rzeczywistych.
Zobaczymy też, że:
Dla amplitud lub wartości skutecznych jednak prawo
Ohma obowiązuje, a prawa Kirchhoffa NIE!!!
Okazuje się, że dla wartości chwilowych pochodną
można zastąpić mnożeniem w sytuacji, gdy mamy do
czynienia z przebiegami sinusoidalnymi i ich
zapisem zespolonym.
Zobaczmy to dokładniej. Z definicji pojemności mamy:
Q = CU
Przy zmianach ładunku:
dQ/dt = CdU/dt
I = CdU/dt
U = Umaxcos(ωt+φ) uzyskamy:
I = CdU/dt = CUmaxd(cos(ωt+φ))/dt =
ωCUmax (-sin(ωt+φ)) = ωCUmax(cos(ωt+φ +90o))
Mając napięcie sinusoidalne
Czyli prąd w kondensatorze uzyskaliśmy mnożąc przez ωC napięcie, któremu
zmieniliśmy fazę o 90o. To oznacza, że mając prąd wystarczy podzielić go
przez ωC i przesunąć (cofnąć) jego fazę o -90o i otrzymamy napięcie.
nie ma tu współczynnika
proporcjonalności między chwilowymi
!wartościami prądu i napięcia
Widać, że
Jeżeli jednak funkcję U = Umaxcos(ωt+φ) potraktujemy jako część
rzeczywistą wielkości zespolonej Umaxej(ωt+φ) to:
U = Re(Umaxej(ωt+φ))
I = Cd(Umaxej(ωt+φ))dt = jωCUmaxej(ωt+φ)
I = jωCU = BCU
gdzie
BC = jωC
U = I/jωC = XCI
gdzie XC=
albo
1/jωC
Zatem w zapisie zespolonym dla wartości chwilowych jest
współczynnik! Jest prawo Ohma dla pojemności!
BC – taka przewodność
to susceptancja
Ilustracja. Jeżeli przez kondensator płynie jakiś prąd
zmienny to na tym kondensatorze mamy też zmienne
napięcie. Prawo Ohma dla kondensatora, którego reaktancją jest
XC= 1/jωC = -j/ωC = [1/ωC] e-jπ/2 ,
i w którym mamy prąd I = Imaxej(ωt+φ) wyrażamy tak:
U = I⋅XC = Imaxej(ωt+φ) ⋅ 1/ωCe-jπ/2 = Imax/ωC ej(ωt+φ-π/2);
widzimy tu iloczyn modułów Imax i 1/ωC jako moduł napięcia a w
wykładniku do aktualnego kąta prądu dodany kąt ujemny: –π/2
Zatem napięcie U ma tu w każdej chwili fazę przesuniętą o –π/2
względem fazy prądu.
Wniosek:
Pomnożenie prądu
przez impedancję Xc daje
napięcie opóźnione o ćwierć kąta pełnego (koresponduje to z prostym
stwierdzeniem, że ładując kondensator na początku ładowania mamy duży
prąd i zerowe napięcie, a po naładowaniu zerowy prąd i maksymalne napięcie).
Cewki indukcyjne.
Modelem indukcyjności jest cewka,
czyli też element z dwoma zaciskami
– dwójnik. Ze względu na rodzaj
rdzenia wyróżniamy cewki: ferrytowe,
metalowe, powietrzne.
Cewka realizuje ideę magazynowania
energii kinetycznej prądu elektrycznego,
który wytwarza pole magnetyczne.
Schemat zastępczy
Indukcyjność ma taką własność,
że prędkość zmian jej prądu jest
proporcjonalna do panującego na niej napięcia.
Tu stałe napięcie wymusza stały wzrost prądu.
L jest indukcyjnością cewki.
Z takiej relacji między prądem a napięciem wynika, że
dla wartości chwilowych prądu i napięcia na cewce
też nie działa prawo Ohma.
Mamy związek: U = LdI/dt, załóżmy że
wymuszamy prąd sinusoidalny w cewce:
I = Imaxcos(ωt+φ)
U = LdI/dt = LImaxd(cos(ωt+φ))/dt =
ωLImax (-sin(ωt+φ)) = ωLImax(cos(ωt+φ+90o))
Czyli napięcie na cewce uzyskaliśmy mnożąc przez ωL prąd, któremu jeszcze
zmieniliśmy fazę o 90o. To oznacza, że mając prąd wystarczy pomnożyć go
przez ωL i przesunąć jego fazę o 90o i
otrzymamy napięcie. Widać, że
nie ma tu współczynnika proporcjonalności
między prądem a napięciem!
Jeżeli jednak funkcję I = Imaxcos(ωt+φ) potraktujemy jako
część rzeczywistą wielkości zespolonej Imaxej(ωt+φ) to:
I = Re(Imaxej(ωt+φ))
U = Ld(Imaxej(ωt+φ))dt = jωLImaxej(ωt+φ)
U = jωLI = XLI gdzie XL= jωL albo I =
(1/jωL)U = BLU gdzie BL = 1/jωL
Jest współczynnik!
Jest prawo Ohma dla indukcyjności!
Zatem w zapisie zespolonym:
XL – reaktancja cewki
BL – susceptancja cewki
Ilustracja. Jeżeli przez cewkę płynie jakiś prąd
zmienny to na jej zaciskach mamy też zmienne
napięcie. Prawo Ohma dla indukcyjności, której impedancją jest
XL= jωL = ωLejπ/2
i w której mamy prąd I = Imaxej(ωt+φ) wyrażamy następująco:
U = I⋅XL = Imaxej(ωt+φ) ⋅ ωLejπ/2 = ImaxωLej(ωt+φ+π/2);
widzimy tu iloczyn modułów Imax i ωL jako moduł napięcia a w
wykładniku do aktualnego kąta prądu dodany kąt dodatni: π/2
Zatem napięcie U ma tu w każdej chwili fazę przesuniętą o π/2
względem fazy prądu.
Wniosek:
Pomnożenie prądu
przez impedancję XL daje
napięcie wyprzedzające o ćwierć kąta pełnego prąd. Koresponduje to z
prostym stwierdzeniem, że na początku rozpędzania ładunku mamy jeszcze
zerowy prąd a maksymalne napięcie. Gdy prąd osiągnie maksymalną wartość
to napięcie odpowiedzialne za jego zerowe zmiany jest zerowe!
Chociaż i tu nie występuje proporcjonalność między chwilowymi
wartościami napięcia i prądu. Zachodzi jednak proporcjonalność między
wartościami skutecznymi lub amplitudami (tj. modułami czyli
wartościami maksymalnymi, ale pojawiającymi się niejednocześnie występuje przesunięcie fazowe). Jak widać dla indukcyjności i
pojemności współczynniki XL i XC są czysto urojone zatem wektory
prądu z wektorami napięcia tworzą kąty proste. To oznacza, że iloczyn
skalarny U • I - moc tracona w idealnym kondensatorze lub
indukcyjności jest zerem?! Ten efekt odróżnia kondensatory i cewki od
rezystorów. W rzeczywistości mamy do czynienia z pewnymi stratami
mocy w dielektryku kondensatora i rdzeniu cewki. W obwodach LC
dominujące są jednak straty mocy na rezystancji uzwojenia cewki.
Zachowanie się cewek i kondensatorów zależy od częstotliwości
sygnału elektrycznego bo impedancje XL i XC zależą od ω.
„Dławik” to solenoid o dużej indukcyjności pełniący rolę dużej
impedancji dla prądów zmiennych.
Szeregowy obwód RLC.
Stosując napięciowe prawo Kirchhoffa
do pojedynczego „oczka” na rysunku
obok, możemy napisać równanie:
u(t) = uR(t) + uL (t) + uC(t)
Przykładając sinusoidalne napięcie:
u(t) = Umej(ωt+φ) musimy otrzymać prąd:
i(t) = Imej(ωt+ψ) (periodyczna przyczyna
to i periodyczny skutek).
Wstawmy zatem do równania obwodu wyrażenie: i(t) = I mej(ωt+ψ). Otrzymamy:
Umej(ωt+φ) = RImej(ωt+ψ) + (1/C)∫Imej(ωt+ψ) dt + Ld(Imej(ωt+ψ))/dt.
Umej(ωt+φ) = RImej(ωt+ψ) + (1/jωC)Imej(ωt+ψ) + jωLImej(ωt+ψ)
Umej(ωt+φ) = Imej(ωt+ψ)(R+ 1/jωC + jωL)
Umej(ωt+φ) = Imej(ωt+ψ)(R+ j(ωL – 1/ωC))
Umej(ωt+φ) = Imej(ωt+ψ)(R2 + (ωL – 1/ωC)2)0,5ej·arctg((ωL – 1/ωC)/R) ->
U = I Z czyli:
UZespolone napięcie = IZespolony prąd ·ZImpedancja zespolona.
Umej(ωt+φ) = Imej(ωt+ψ)(R2 + (ωL – 1/ωC)2)0,5ej·arctg((ωL – 1/ωC)/R)
U = I Z czyli:
UZespolone napięcie = IZespolony prąd ·ZImpedancja zespolona.
Zespolona impedancja szeregowo połączonych R, L i C ma zatem postać:
Z = R+ j(ωL – 1/ωC) = R + j(XL – XC) = R +X = Zejθ,
możemy też zapisać:
Z = R + XL + XC, Z = Z1 + Z2 + Z3. Ponadto U = I Z po rozpisaniu:
U = IZ1 + IZ2 + IZ3
opisuje dzielnik napięcia zależny od ω.
Dzielniki napięcia zawierające elementy typu C lub L mogą dzielić napięcie zależnie od częstotliwości. Zatem
mogą zmieniać kształt sygnału, sygnał wyjściowy jest
inny od wejściowego, chociaż są to elementy liniowe!
Podobnie działają dzielniki prądu zawierające elementy
typu C lub L – dzielą prąd zależnie od częstotliwości.
Dla układów R L C obowiązuje uogólnione prawo Ohma:
U = I⋅Z, I = Y⋅U, gdzie Y = 1/Z, Z - impedancja, Y –
admitancja, i wszystkie wielkości są wyrażane w postaci
zespolonej.
Obliczanie wypadkowej impedancji Zw dla układu
złożonego z elementów Z1, Z2, ....Zn, odbywa się
podobnie jak obliczanie wypadkowej rezystancji układu
złożonego z elementów R1, R2,.... Rn. Różnicę daje tylko
samo zastosowanie liczb zespolonych.
Należy pamiętać,
że rzeczywistą wartością chwilową napięcia jest: U(t) = Re(U(t)).
Rzeczywistą wartością chwilową prądu jest I(t) = Re(I(t)).
Impedancję wyrażamy jako:
Z = R + X,
zawada = oporność czynna + oporność bierna =
rezystancja + reaktancja,
gdzie: X = XL + XC, XL = jωL i XC = 1/jωC.
R jest rezystancją, a jωL i 1/jωC nazywamy
reaktancjami, impedancjami biernymi.
Admitancje to (odwrotności impedancji = „drożności”)
Y = 1/Z = G+jB, G = 1/R - konduktancja, B = 1/X susceptancja, YC = jωC, YL= 1/jωL.
Jednostką admitancji jest Simens 1S = 1/Ω.
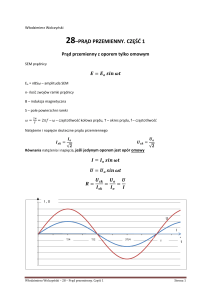
Przykład 3.1. Wiedząc, że w układzie obok jest prąd
zmienny o natężeniu I = 5cosωt A, ω = 2π50 rad/s =
314 rad/s, R = 0,5 Ω, L = 1 mH, C = 4 mF, obliczyć
wszystkie napięcia.
Rozw. UR = IR = (5cosωt A)(0,5 Ω) = 2,5cosωt V, lub
UR = [5(cosωt +jsinωt) A](0,5 Ω) = 2,5(cosωt +jsinωt) V,
albo: UR = (5ejωt A)(0,5 Ω) = 2,5ejωt V = 2,5∠0 V
UL = IXL = I (jωL) = [5(cosωt + jsinωt) A](j0,314 Ω) =
1,57(- sinωt + jcosωt) V = 1,57[cos(ωt + π/2) + jsin(ωt +
π/2)] V, albo
UL = 5ejωt0,314ejπ/2 AΩ = 1,57ej(ωt+π/2) V = 1,57∠π/2 V.
UC = IXC = I(1/jωC) = I(-j/ωC) = (5ejωt A)(-j/1,26 Ω) =
5ejωt0,796e-jπ/2 = 3,98ej(ωt-π/2) V = 3,98∠-π/2 V.
U = UR + UL + UC, dla t = 0: U = 2,5 V + 1,57[jsin(0 +
π/2)] V + 3,98[jsin (0 - π/2)] V =[2,5 + j1,57 - j3,98] V =
2,5 V – j 2,41 V. Arctan(-2,41/2,5) = -0,767rad.
(2,52 + 2,412)0,5=3,47 -> U = 3,47ej(ωt - 0,767) V=
3,47∠-0,767 V.
U = 3,47ej(ωt - 0,767) V
graficzna ilustracja tego wyniku : ->
Wykresy wskazowe
Wskaz, fazor (ang. phasor) jest liczbą
zespoloną AejΦ i wektorem na płaszczyźnie
zespolonej reprezentującym sinusoidalny
przebieg Acos(ωt +Φ).
Np. u(t) = Umaxcos(ωt +Φ) = Re[Umaxej(ωt +Φ)] =
Re[UmaxejΦ ejωt]. Wskazem napięcia jest tu
UmaxejΦ (taki wskaz bywa zapisywany jako:
Umax∠Φ) czyli jest to zespolona postać
napięcia U w pewnej dogodnej chwili t
(zwykle t = 0).
Zatem wykres wskazowy do poprzedniego
przykładu można przedstawić jak obok:
Podkreślmy, że fazorem (wskazem) F = Fmejφ nazywamy wielkość zespoloną,
która reprezentuje funkcję sinusoidalnie zmieniającą się w czasie. Zbiorem
wartości F = Fmej(ωt+φ) jest okrąg o promieniu Fm ze środkiem w początku układu
płaszczyzny zespolonej (Re, Im). Wykresem wskazowym nazywamy graficzną
prezentację napięć i prądów sinusoidalnych w danym układzie prądu
zmiennego o zadanej częstotliwości. Wykres ilustruje wielkości amplitud
prądów i napięć oraz ich relacje fazowe w układzie w stanie stacjonarnym (tj.
po czasie od włączenia źródeł znacznie dłuższym od okresu oscylacji T).
Pojedynczy wykres dotyczy jednej wybranej częstotliwości. Wykresy wskazowe
są też graficzną ilustracją równań jakie dają nam prawa Kirchhoffa oczywiście
zapisane w postaci zespolonej. Dlatego początkujący często wykreślają
wskazy na płaszczyźnie zespolonej z zaznaczonymi osiami Im i Re. W
rzeczywistości na takiej płaszczyźnie wszystkie wektory powinny wirować
zgodnie z pulsacją ω, natomiast wykres jest uchwyceniem ułożenia wektorów
w określonej, dogodnej chwili (np. gdy jakiś prąd lub napięcie przechodzi przez
swoje maksimum). Z wykresu znajdujemy relacje między długościami wektorów
(tj. amplitudami) napięć i prądów oraz ich względne przesunięcia fazowe.
Wykresy wskazowe są szeroko stosowane w elektrotechnice (tu zamiast
amplitud można spotkać wartości skuteczne przy analizie przekazu mocy).
Przy analizie filtrów mogą stanowić dogodną ilustrację relacji między sygnałem
wejściowym i wyjściowym danego filtra dla wybranej częstotliwości.
Ważne!
W przykładach, w których zastosujemy zapis
wielkości w postaci zespolonej należy zauważyć, że:
1) Do zapisu równań będących prawami Kirchhoffa
wstawiamy wszystkie napięcia, prądy i impedancje w
postaci zespolonej. Prawa Kirchhoffa nie obowiązują
dla wartości skutecznych i dla modułów czyli
amplitud. Oczywiście po napisaniu równania
możemy wziąć moduły obu stron (całych stron!).
2) Gdy prawo Ohma jest treścią równania (jedna
wielkość = iloczyn lub iloraz dwu innych) to możemy
go zapisać nie tylko dla wielkości zespolonych ale
również dla modułów i dla wartości skutecznych.
Przykład 3.2. Obliczyć zawadę układu
oraz natężenie prądu po przyłożeniu
Napięcia U = 240cos(314t).
Rozw.
Z = XL+ R + XC = R + jωL – j/ωC =
1Ω + j(ω10-6 - 1/ω10-6)Ω =
1Ω + j(3,1410-4 - 1/(3,14⋅10-4))Ω =1Ω + j3183Ω =
3183∠89,98° Ω.
I = U/Z = 240∠0°/ 3183∠89,98° A =
75,4mV∠-89,98° A.
Przykład 3.3. Obliczyć zależność zawady od ω.
Rozw. Z = XL + XCR/(R + XC) =
jωL – j(R/ωC)/(R – j/ωC) =
jω – j(1012/ω)/(106 – j106/ω) = jω – j106/(ω – j)
= 106/(ω2 + 1) + jω(1 – 106/(ω2 + 1)).
Przykład 3.4. Znajdź zastępczy układ Thevenina
podanego układu.
Rozw. Z punktu widzenia zacisków: Z1 II Z2,
Jeżeli Z1 i Z2 są równoległe to ZT obliczymy
ze wzoru na zastępczą impedancję połączenia
równoległego:
Równoległy obwód RLC.
Aby wyznaczyć częstotliwość rezonansową tego układu
pomożemy sobie wykresem wskazowym, na którym
umieścimy prądy i niektóre napięcia w tym obwodzie.
Wymuszenie: u = U0ej(ωt + 0),
IC = u/(-j/ωC) = juωC,
IRL = u/(R + jωL) = u(R - jωL)/(R2 + ω2L2)
Wybierając moment gdy u jest czysto
rzeczywiste czyli wektor u leży na osi „Re”
narysujemy: u = u = U0,
IRL = u(R - jωL)/(R2 + ω2L2)
IC = juωC,
Re(IRL) = uR/(R2 + ω2L2)
Im(IRL) = -uωL/(R2 + ω2L2).
Z wykresu wskazowego widać, że dla uzyskania zgodności fazy wypadkowego
prądu (czyli sumy IC i IRL) z fazą napięcia wymuszającego Im(IC) + Im(IRL) = 0
czyli: Im(I ) = - Im(I ).
Równoległy obwód RLC.
IRL = u(R - jωL)/(R2 + ω2L2)
IC = juωC,
Re(IRL) = uR/(R2 + ω2L2)
Im(IRL) = -uωL/(R2 + ω2L2).
| Im(IC) | = | Im(IRL) |
Im(IC) = -Im(IRL)
uωC = uωL/(R2 + ω2L2);
C = L/(R2 + ω2L2);
R2 + ω2L2 = L/C
ω2L2 = L/C – R2
ω2= 1/LC – R2/L2
ωr = (1/LC – R2/L2)1/2
E-E-M. Lista-03
1. Mając dwie liczby zespolone A = 3 + j3, B = 1 + j√3, oblicz AB oraz A/B.
2. Narysować wykres wskazowy dla szeregowo połączonych rezystora 10Ω i
kondensatora 1mF, przez które płynie prąd I = 2sin(2π50t) A. Oblicz całkowite
napięcie przyłożone do układu RC oraz różnice faz między prądem i wszystkimi
napięciami.
3. Do indukcyjności L = 1 mH o rezystancji uzwojenia 1Ω należy dołączyć
szeregowo kondensator tak aby uzyskać rezonans dla częstotliwości 1MHz.
Narysować wykres wskazowy dla zasilania napięciem U = 1Vsin(2π106t).
4. Obliczyć zawadę układu dla częstotliwości kątowej
(pulsacji) 1rad/s i 1Mrad/s. Obliczyć różnicę faz między
przyłożonym napięciem a prądem w tym układzie.
5. Oblicz zawadę układu dla pulsacji 1rad/s i 1Mrad/s.
Oblicz różnicę faz między napięciem i prądem w tym
układzie.
6. Narysuj wykres wskazowy i obliczyć wartości przepięcia
w rezonansie układu dla R = 1 Ω, i R = 0,1 Ω przy zasilaniu
napięciem o amplitudzie 1 V.
7. Znajdź częstotliwość rezonansową dla układu.
Dodatek dla opornych.
Co znaczą następujące zapisy?
1) I = Icos(ωt +β) = Iamplitudacos(ωpulsacja tczas + βkąt początkowy dla t = 0s)
jest to zapis kosinusoidalnego (sinusoidalnego) przebiegu
natężenia prądu.
2) I = Icos(ωt +β) + jIsin(ωt +β) = Iej(ωt +β) oznacza ten sam prąd co w punkcie
poprzednim ale zapisanym w postaci zespolonej pozwalającej łatwo czynić
poprawne obliczenia!
Jeżeli zamiast informacji, że I = 5cos(ωt + π/2) otrzymamy informacje że w
pewnej chwili t = 0 s prąd miął natężenie I = 0 A to nie wiemy czy w następnych
chwilach prąd będzie niezerowy. Gdy jednak informacją będzie, że danej
chwili I = 0 + j5 [A] = j5 A to wiemy, że chociaż teraz I = 0 A to po chwili już
I ≠ 0 A, a w pewnej chwili będzie 5 A!!!
Na elementach obwodu prądu sinusoidalnie zmiennego występują
napięcia dające się zapisać jako U = Umaxcos(ωt+φ). Funkcje takie
możemy traktować jako części rzeczywiste periodycznych funkcji
zespolonych U = Umaxej(ωt+φ) czyli U = Re(U = Umaxej(ωt+φ)). Gdy tak
zapisane napięcie pojawi się na kondensatorze to z relacji między
prądem i napięciem dla kondensatora:
I = CdU/dt
wynika, że dla prądów zmiennych impedancja kondensatora czyli
współczynnik („proporcjonalności”) między prądem i napięciem
wyraża się funkcją zespoloną:
ZC = XC = 1/jωC.
bo podstawiając zespoloną postać napięcia: U =
Umej(ωt+φ) do wyrażenia I = CdU/dt otrzymujemy: I =
CjωU, mamy mnożenie zamiast pochodnej! Z tego, że I =
CjωU mamy: U = I/jωC,
U = (1/jωC)I, albo krócej: U = XCI, XC= 1/jωC
U = XCI jest prawem Ohma dla kondensatora zapisanym przy
pomocy funkcji zespolonych! Mamy to dzięki temu, że operator
różniczkowania działając na ejωt daje tyle co proste pomnożenie
przez stałą jω (tj. współczynnik przy t wykładnika w ejωt)* . W
dziedzinie liczb zespolonych mnożenie daje, oprócz zmiany
modułu, również obrót wektora! Wielkość 1/jωC nazywamy
reaktancją (lub impedancją) kondensatora. Zespolony spadek
napięcia na idealnym kondensatorze jest iloczynem zespolonego
natężenia prądu i impedancji XC (czysto urojonej).
Istotną wadą rzeczywistych kondensatorów jest ich upływność i
tzw. straty w dielektryku a dla prądów o wysokiej częstotliwości
dodatkowy problem stanowi indukcyjność doprowadzeń i okładek.
Do zamiany równań różniczkowo-całkowych na równania
algebraiczne w wielu dziedzinach techniki stosowana jest
transformata Laplace’a. W bieżącym wykładzie ograniczamy się
do stosowania liczb zespolonych.
*