Weryfikacja założeń modelu Gaussa

Weryfikacja założeń modelu Gaussa-Markowa
Przypomnienie: W modelu Gaussa-Markowa Y = X
jedynym losowym elementem jest wektor .
2
Zakładamy, że jest wektorem niezależnych zmiennych losowych o jednakowym rozkładzie N ,
,
2
gdzie
jest nieznane.
Weryfikacja założeń modelu Gaussa-Markowa sprowadza się do weryfikacji założeń o wektorze . Ponieważ
wektor jest nieznany, nieznana jest też realizacja wektora . Wobec tego testowanie weryfikacja założeń
modelu Gaussa-Markowa opiera się na wektorze reszt e= Y − X , który traktujemy jako swoisty estymator
wektora błędów .
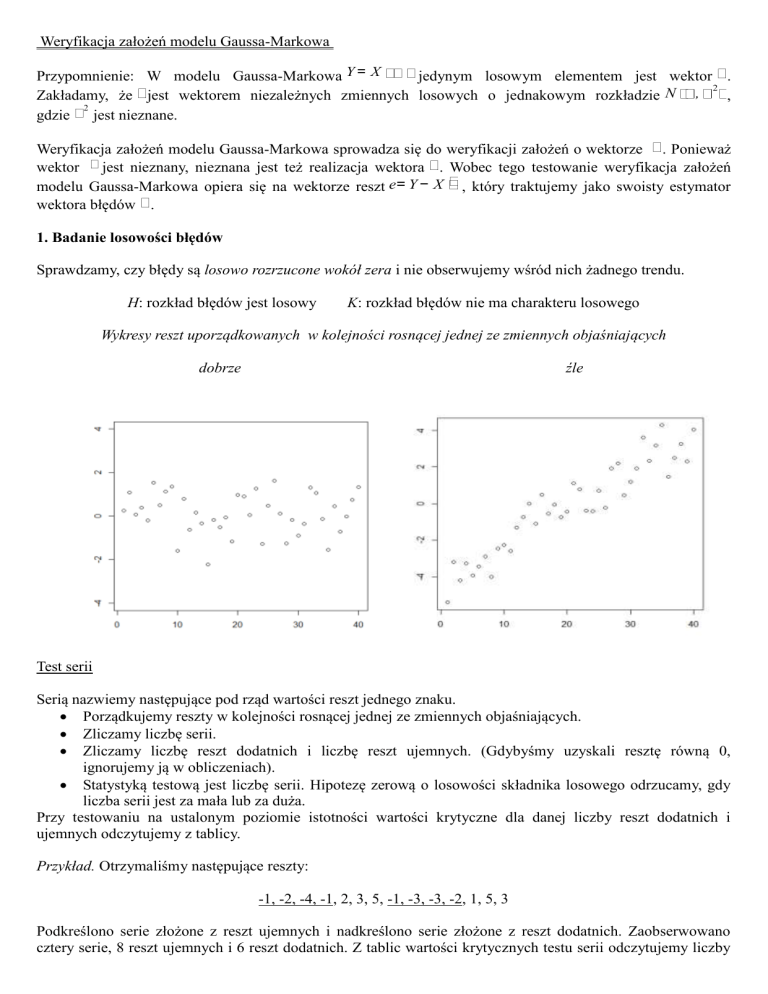
1. Badanie losowości błędów
Sprawdzamy, czy błędy są losowo rozrzucone wokół zera i nie obserwujemy wśród nich żadnego trendu.
H: rozkład błędów jest losowy
K: rozkład błędów nie ma charakteru losowego
Wykresy reszt uporządkowanych w kolejności rosnącej jednej ze zmiennych objaśniających
źle
dobrze
Test serii
Serią nazwiemy następujące pod rząd wartości reszt jednego znaku.
 Porządkujemy reszty w kolejności rosnącej jednej ze zmiennych objaśniających.
 Zliczamy liczbę serii.
 Zliczamy liczbę reszt dodatnich i liczbę reszt ujemnych. (Gdybyśmy uzyskali resztę równą 0,
ignorujemy ją w obliczeniach).
 Statystyką testową jest liczbę serii. Hipotezę zerową o losowości składnika losowego odrzucamy, gdy
liczba serii jest za mała lub za duża.
Przy testowaniu na ustalonym poziomie istotności wartości krytyczne dla danej liczby reszt dodatnich i
ujemnych odczytujemy z tablicy.
Przykład. Otrzymaliśmy następujące reszty:
-1, -2, -4, -1, 2, 3, 5, -1, -3, -3, -2, 1, 5, 3
Podkreślono serie złożone z reszt ujemnych i nadkreślono serie złożone z reszt dodatnich. Zaobserwowano
cztery serie, 8 reszt ujemnych i 6 reszt dodatnich. Z tablic wartości krytycznych testu serii odczytujemy liczby
4 i 11. Liczba serii należy do zbioru krytycznego {s : s 4∧ s 11} , a zatem na poziomie istotności 0,05 (na
takim poziomie istotności jest sporządzona tablica) odrzucamy hipotezę o losowości składnika losowego na
rzecz hipotezy o tym, że składnik losowy nie ma charakteru losowego.
Uwaga: Należy zwrócić baczną uwagę, czy w tablicy, z jakiej korzystamy, podano wartości krytyczne z ostrymi
czy słabymi nierównościami tzn. czy zbiór krytyczny jest postaci
{s : s s L∧ s sU } czy też {s : s s L∧ s sU } .
Wykazany brak losowości błędów świadczy o tym, że badana zależność nie ma charakteru liniowego
(przynajmniej względem jednej zmiennej, przy porządkowaniu względem której odkryto brak losowości
błędów) bądź też że brak jest w modelu istotnych zmiennych niezależnych, lub też że występuje autokorelacja
składnika losowego (patrz: dalsza część wykładu). Testowanie losowości błędów może być więc traktowane
jako testowanie słuszności struktury przyjętego modelu.
2. Badanie normalności błędów
Wykres kwantylowo-kwantylowy
Wykres kwantylowo-kwantylowy w ogólności
Przypomnijmy:
Dystrybuantą
zmiennej
F
t
=
P
X
t
X
wzorem
.
Niech X 1, X 2,
losowa X .
Def.
losowej X
funkcję F X :ℝ [0,1] zadaną
nazywamy
, X n będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie takim jak zmienna
Dystrybuantą
empiryczną
wyznaczoną
na
1
funkcję F n : R [0,1] zadaną wzorem F n t = n ∣{i : X i t}∣ .
postawie
próby
X 1, X 2,
, X n nazywamy
Tw. (Gliwenko-Cantelli)
P lim n ∞ s u p t ∈ℝ∣F n t − F X t ∣ = 1
(tzn. dystrybuanta empiryczna jest z prawdopodobieństwem 1 zbieżna jednostajnie do dystrybuanty).
−1
Def. Funkcją kwantylową rozkładu zmiennej losowej X nazywamy funkcję F X : 0,1
F −X1 u = inf {t ∈ℝ : F x t u } .
ℝ daną wzorem
Jeśli dystrybuanta zmiennej losowej X jest funkcją ciągłą i ściśle rosnącą, to wówczas funkcja kwantylowa
zmiennej losowej X jest funkcją odwrotną w zwykłym sensie do dystrybuanty zmiennej losowej X .
Def. Empiryczną funkcją kwantylową wyznaczoną na
−1
−1
funkcję F n : 0,1 ℝ zadaną wzorem F X u = inf {t ∈ℝ : F n t
postawie
u} .
próby
X 1, X 2,
, X n nazywamy
Tw.
∀ 0 a b 1 P lim n ∞ s u pu∈[a ,b]∣F −n 1 u − F −X1 u ∣ = 1
(tzn. empiryczna funkcja kwantylowa jest z prawdopodobieństwem 1 zbieżna niemal jednostajnie do funkcji
kwantylowej).
Dystrybuanta empiryczna jest funkcją schodkową, prawostronnie ciągłą. Jej kolejne skoki wypadają
w punktach X 1 , X 2 , , X n , gdzie X 1 , X 2 , , X n oznaczają statystyki pozycyjne (porządkowe) z próby
1 2
n− 1
, , ,
, 1 . Ściślej mówiąc,
X 1, X 2, , X n , a zbiór wartości zawiera się w zbiorze
n n
n
{
∀ k ∈ {1, 2,
, n− 1} ∀ t ∈ [ X
}
k
,X
k 1
Fn t =
k
n.
Empiryczna funkcja kwantylowa jest funkcją schodkową, lewostronnie ciągłą. Jej kolejne skoki wypadają
1 2
n− 1
, , ,
, 1 , a zbiór wartości zawiera się w zbiorze {X 1 , X 2 , , X n } .
w punktach ze zbioru
n n
n
Ściślej mówiąc,
k− 1 k
∀ k ∈ {1, 2, , n− 1} ∀ u ∈
,
F −n 1 u = X k .
n n
{
}
]
Ze względu na zbieżność empirycznej funkcji kwantylowej do funkcji kwantylowej w każdym punkcie
−1
−1
(własność słabsza od zbieżności niemal jednostajnej), punkty postaci F n u , F X u , u∈ 0,1 powinny
leżeć mniej więcej na prostej o równaniu y= x .
−1
2
−1
Niech m, będzie funkcją kwantylową rozkładu N m ,
zaś
– funkcją kwantylową rozkładu N 0,1 .
Zachodzi tożsamość:
−1
−1
∀ u∈ 0,1
u =m
u .
m,
X 1, X 2, , X n pochodzi z rozkładu normalnego, to punkty postaci
Wobec tego jeśli próba
−1
−1
Fn u ,
u , u ∈ 0,1 leżą na prostej.
2
2
k−
Niech u =
k
n
1
2
, k = 1, 2,
F −n 1 u k = X
, n . Wówczas
k
.
−1
u k , k= 1, 2, , n , nazywamy wykresem kwantylowo-kwantylowym
Def. Zbiór punktów postaci X k ,
zgodności z rozkładem normalnym, sporządzonym na podstawie próby X 1, X 2, , X n .
Jeśli punkty na wykresie kwantylowo-kwantylowym nie układają się w prostą, świadczy to o tym, że
obserwacje X 1, X 2, , X n nie pochodzą z rozkładu normalnego.
Wykres kwantylowo-kwantylowy w badaniu normalności błędów
W układzie współrzędnych zaznaczamy punkty postaci e k ,
−1
k−
uk
, gdzie u =
k
1
2
, k = 1, 2,
n
punkty nie układają się w prostą, świadczy to o tym, że błędy nie mają rozkładu normalnego.
, n . Jeśli
Test Shapiro–Wilka
Test Shapiro–Wilka w ogólności
X 1, X 2, , X n – niezależne zmienne losowe o jednakowym rozkładzie
H: rozkład ów jest rozkładem normalnym
K: rozkład ów nie jest rozkładem normalnym
Statystyka testowa:
T=
n
[
]
∑2 a
i= 1
i
n
X
∑ i= 1
n− i 1
−X
X i− X
2
i
2
gdzie X 1 , X 2 , , X n oznaczają statystyki pozycyjne (porządkowe) z próby X 1, X 2, , X n . Hipotezę
zerową odrzucamy dla małych wartości statystyki testowej. Liczby a 1, a 2, oraz punkt krytyczny dla
testowania na ustalonym poziomie istotności odczytujemy z tablic.
Konstrukcja testu Shapiro–Wilka
Niech
2
= Var X 1 . Wówczas przy hipotezie zerowej zmienne losowe
X 1− X X n− X
,
,
,
X n− X
są mniej
więcej niezależnymi zmiennymi losowymi o rozkładzie N 0,1 . Niech
X 1− X X 2 − X
X n− X
X=
'
Przy hipotezie zerowej jest to mniej więcej wektor statystyk pozycyjnych z próby z rozkładu N 0,1 .
Y 1, Y 2, , Y n
Niech
będą niezależnymi zmiennymi losowymi o rozkładzie N 0,1 . Niech
mn ' (czyli m jest wektorem statystyk pozycyjnych z rozkładu
mi= EY i , i= 1, 2, , n . Niech m= m1 m2
N 0,1 ). Niech V będzie macierzą kowariancji wektora m .
Niech
1
a= − 1 V − 1 m .
∥V m∥
a
Możemy powiedzieć, że
jest wektorem statystyk pozycyjnych z rozkładu N 0,1 poddanym pewnemu
przekształceniu związanemu z macierzą kowariancji wektora statystyk pozycyjnych z rozkładu
N 0,1 i unormowaniu (tzn. ∥a∥= 1 ). Zauważmy, że a n− i 1= − a i , i= 1,2 , , n .
2
n
X i− X
2
∑ i = 1 ai⋅
a° X 2
a° X 2
a° X
2
cos
a, X =
=
=
=
2 =
∥a∥2⋅∥ X ∥ 2 ∥ X∥2
∥a∥2⋅∥ X∥2
n
Xi− X
[
1
n
∑ i= 1 a i⋅
2⋅
=
1
n
]
2
X i− X
2⋅ ∑ i = 1 X i − X
2
n
=
∑ i= 1 a i⋅ X i − X
n
2
∑ i= 1 X i − X
∑ i=1
2
n
=
∑ i = 1 a i⋅ X i − X
n
2
∑ i= 1 X i − X
O niespełnieniu hipotezy zerowej świadczy duża miara kąta
tego kąta.
2
=
n
[
]
∑2 a
i= 1
i
n
X
∑ i= 1
n− i 1
−X
X i− X
2
i
2
a , X a więc mała wartość kwadratu cosinusa
Test Shapiro–Wilka w testowaniu normalności błędów
H: błędy są niezależnymi zmiennymi losowymi o tym samym rozkładzie normalnym
K: błędy nie są niezależnymi zmiennymi losowymi o tym samym rozkładzie normalnym
Statystyka testowa:
[n ]
∑ i=2 1 a i e n− i 1 − e i
T=
n
∑ i= 1 e 2i
2
.
Hipotezę zerową odrzucamy dla małych wartości statystyki testowej. Liczby a 1, a 2,
testowania na ustalonym poziomie istotności odczytujemy z tablic.
oraz punkt krytyczny dla
3. Badanie niezależności błędów
Mówienie o potencjalnej zależności błędów jest najbardziej zasadne, gdy obserwacje indeksowane są czasem.
Wówczas może się zdarzyć, że błąd w chwili i jest zależny od przeszłości tzn. od błędów w chwilach
i− 1, i− 2, . Najczęściej zakładamy, że błędy tworzą proces autoregresji rzędu p ( AR p )tzn.
i = 1 i− 1
2 i− 2
p i− p .
Ponieważ zmienne losowe o rozkładzie normalnym są niezależne wtedy i tylko wtedy, gdy są nieskorelowane,
a w modelu Gaussa-Markowa błędy mają rozkład normalny, więc brak podstaw do odrzucenia hipotezy o braku
korelacji z przeszłością (autokorelacji) jest w rozważanym modelu równoważne brakowi podstaw do
odrzucenia hipotezy o niezależności błędów.
Test Durbina–Watsona
Zakładamy, że błędy mają rozkład normalny o stałej wariancji i tworzą proces AR 1 tzn.
=
1 i− 1 .
Możliwe są dwa problemy testowania hipotez:
 brak autokorelacji przeciwko dodatniej autokorelacji rzędu 1 tzn.
H: 1= 0 K: 1 0 ,
 brak autokorelacji przeciwko ujemnej autokorelacji rzędu 1 tzn.
H: 1= 0 K: 1 0 .
i
W obu przypadkach statystyka testowa jest postaci:
∑ i= 2 e i− ei − 1 2
T=
n
.
∑ t= i e 2i
n
n
n
e 2i − 2 e i e i− 1 e 2i− 1 ∑ i = 2 e 2i
∑ i= 2 ei e i− 1 ∑ i= 2 e 2i− 1
= n
− 2⋅
≈
n
n
n
∑ t= i ei2
∑ t = i e 2i
∑ t= i ei2
∑ t= i ei2
n
∑ i = 2 ei − e ei − 1− e
1= 2− 2⋅
= 2− 2 1 = 2 1− 1
n
2
∑ t= i e i− e
n
∑ i= 2 e i− ei − 1 2 ∑ i= 2
T=
=
n
∑ t= i e 2i
n
∑ i= 2 ei e i− 1
≈ 1− 2
n
∑ t= i e 2i
n
n
(Estymator 1 występuje w teorii szeregów czasowych). Ponieważ 1 ∈[− 1,1] , więc T ∈[0,4] . O wyraźnej
dodatniej autokorelacji rzędu 1 świadczy 1 bliskie 1 czyli wartości statystyki testowej bliskie 0. O wyraźnej
ujemnej autokorelacji rzędu 1 świadczy 1 bliskie − 1 czyli wartości statystyki testowej bliskie 4.
Przeprowadzając test na ustalonym poziomie istotności, odczytujemy z tablic liczby d U i d L . Następnie
sytuujemy statystykę testową w jednym z trzech obszarów.
Przypadek 1. H:
0
K:
1
0
dL
odrzucamy H na rzecz K
Przypadek 2. H:
0
=0
1
=0
1
K:
1
brak podstaw do odrzucenia H na rzecz K
obszar niekonkluzywny
dU
brak podstaw do odrzucenia H na rzecz K
4
0
4− d U
obszar niekonkluzywny
4− d L
odrzucamy H na rzecz K
4
Test posiada obszar niekonkluzywności czyli obszar, w którym nie można rozstrzygnąć o braku podstaw do
odrzucenia hipotezy H na rzecz hipotezy K lub też o odrzuceniu hipotezy H na rzecz hipotezy K. Dzieje się tak
dlatego, że nie jest możliwe wyznaczenie dokładnego rozkładu statystyki testowej przy hipotezie zerowej
a zatem nie można wyznaczyć dokładnie obszaru krytycznego. Można jedynie oszacować z dołu i z góry punkt
krytyczny. Punkt krytyczny należy do obszaru niekonkluzywnego.
Uwaga: W tablicach statystycznych w wypadku testu Durbina–Watsona liczba zmiennych w modelu oznacza
zazwyczaj liczbę zmiennych nie licząc wyrazu wolnego.
Uwaga: Test Durbina–Watsona charakteryzuje się bardzo małą odpornością na niespełnienie założenia
o normalności rozkładu błędów, dlatego przy wątpliwościach co do spełniania tego założenia przy testowaniu
niezależności błędów należy skorzystać z innego testu, który wykazuje większą odporność na niespełnienie
założenia o normalności.
Ze względu na konieczny wymóg normalności rozkładu błędów oraz możliwość testowania autoregresji tylko
rzędu 1 test Durbina–Watsona ma dziś niewielkie praktyczne zastosowanie. Podajemy go jednak ze względów
historycznych.
Test Breuscha–Godfreya
Zakładamy, że błędy mają rozkład normalny o stałej wariancji i tworzą proces AR p tzn.
i
=
1 i− 1
2 i− 2
p i− p
,
gdzie p jest ustalone i zakładamy o nim, że jest znane.
H:




=
1
=
2
=
p
=0
K:
=0 ∨
=0 ∨
1
∨
2
=0
p
Dokonujemy estymacji parametrów wyjściowego modelu metodą najmniejszych kwadratów
i wyznaczamy wektor e reszt.
Dokonujemy estymacji parametrów modelu:
e i= 0 1 e i− 1
i= p 1, p 2, n .
2 e i− 2
p ei − p ,
2
2
Obliczamy współczynnik determinacji R tego modelu. Statystyka testowa ma postać T = nR .
O prawdziwości hipotezy K świadczy dobre dopasowanie reszt do rozważanego modelu liniowego czyli
2
duża wartość współczynnika determinacji R a zatem duża wartość statystyki testowej.
2
Przy hipotezie H statystyka testowa pod względem rozkładu dąży wraz z n ∞ do rozkładu p .
2 −1
1−
p
Odrzucamy hipotezę H na rzecz K na poziomie istotności , gdy T
.
Uwaga: Ponieważ przy wyznaczaniu obszaru krytycznego bierzemy pod uwagę rozkład graniczny statystyki
testowej przy hipotezie H, więc możliwa jest modyfikacja statystyki testowej o czynnik zbieżny do 1, tak by
2
graniczny rozkład się nie zmienił. Stąd też w literaturze można znaleźć statystykę testową postaci n− k R .
4. Badanie homoskedastyczności (równości wariancji) błędów
H: błędy mają taką samą wariancję (tzn. Var
K: wariancje błędów różnią się
1
= Var
2
=
= Var
n
)
Test Goldfelda–Quandta
Typowa sytuacja, w której zastosowanie ma test Goldfelda-Quandta, to taka, w której po uporządkowaniu reszt
względem którejś zmiennej objaśniającej widzimy, że ich rozrzut jest inny dla małych i dużych wartości tej
zmiennej, względem której odbywa się uporządkowanie.
brak podejrzenia o heteroskedastyczność



podejrzenie o heteroskedastyczność
Porządkujemy reszty w kolejności rosnącej takiej zmiennej objaśniającej, przy porządkowaniu
względem wartości której na wykresie reszt obserwujemy efekt taki jak na rysunku po prawej.
Wybierany n 1 początkowych obserwacji i n 2 końcowych obserwacji (zbiory rozłączne) zgodnie z tym
n1 n2 2
n≈n
≈
uporządkowaniem ( n 1 n 2 n , często w literaturze spotyka się sugestie, by
n
3 i 1 2 ).
Na podstawie każdego z dwóch podzbiorów obserwacji dokonujemy niezależnie estymacji modelu
liniowego, a następnie dokonujemy estymacji wariancji składnika losowego w tych modelach.
2



2
Wyznaczone estymatory wariancji składnika losowego oznaczmy przez 1 i 2 .
2
2
2
2
F n − 1, n − 1 .
Jeśli 1
1 / 2 i przy hipotezie zerowej ma rozkład
1 , to statystyka testowa ma postać
2
2
2
2
F n − 1, n − 1 .
Jeśli 1
2 / 1 i przy hipotezie zerowej ma rozkład
1 , to statystyka testowa ma postać
Odrzucamy hipotezę zerową dla dużych wartości statystyki testowej tzn. testując na poziomie istotności
, odrzucamy hipotezę zerową na rzecz alternatywy, gdy statystyka testowa jest większa od kwantyla
rzędu 1− odpowiedniego rozkładu.
1
2
2
1
Rezygnacja z części obserwacji ( n 1 n 2 n ) ma na celu wyraźniejsze oddzielenie zbiorów, dla których
wariancje składnika losowego są różne. Jeśli jednak usuniemy zbyt dużo obserwacji, obie grupy będą mało
liczne i wnioskowanie będzie przez to niepewne.
Test White'a
H: wariancja błędów jest stała
K: wariancja błędów ma postać wielomianu stopnia 2 zmiennych niezależnych




Dokonujemy estymacji parametrów wyjściowego modelu metodą najmniejszych kwadratów
i wyznaczamy wektor e reszt.
Dopasowujemy do kwadratów reszt wielomian stopnia 2 zmiennych niezależnych.
2
2
Obliczamy współczynnik determinacji R tego modelu. Statystyka testowa ma postać T = nR .
O prawdziwości hipotezy K świadczy dobre dopasowanie reszt do rozważanego modelu liniowego czyli
2
duża wartość współczynnika determinacji R a zatem duża wartość statystyki testowej.
2
Przy hipotezie H statystyka testowa pod względem rozkładu dąży wraz z n ∞ do rozkładu p ,
gdzie p jest liczbą kolumn w macierzy planu modelu, w którym dopasowujemy wielomian. Odrzucamy
2 −1
1−
p
hipotezę H na rzecz K na poziomie istotności , gdy T
.
Uwaga: Niejednokrotnie przy dopasowywaniu wielomianu można pominąć wyrażenia liniowe i w macierzy
planu pozostawić jedynie kolumny odpowiedzialne za wyraz wolny, kwadraty i iloczyni zmiennych
niezależnych.
Uwaga: Jeśli mamy podejrzenie co do tego, które zmienne niezależne mogą być odpowiedzialne za
heteroskedastyczność, do kwadratów reszt możemy dopasować wielomian tylko tych zmiennych.
Uwaga: Testy White'a jako test, w których statystyka testowa jest oparta na współczynniku determinacji, ma
zastosowanie głównie w modelach tylko ze zmiennymi jakościowymi, gdyż w modelach ze zmiennymi
ilościowymi współczynnik determinacji z samej swej natury nie przyjmuje dużych wartości.
Inny test homoskedastyczności powszechnie spotykany w literaturze: test Breuscha-Pagana.
Wykazana heteroskedastyczność błędów może świadczyć również o tym o tym, że badana zależność nie ma
charakteru liniowego bądź też że brak jest w modelu istotnych zmiennych niezależnych. Testowanie
homoskedastyczności błędów może być więc traktowane jako testowanie słuszności struktury przyjętego
modelu.