Potrzeby własne w liniach elektroenergetycznych.

inż. Mieczysław Konstanciak
Potrzeby własne w liniach
elektroenergetycznych.
Wrocław - 2001 r.
-2Spis treści
str.
1. Potrzeby w liniach elektroenergetycznych.........................................................................................................4.
1.1. Potrzeby stanu jałowego...............................................................................................................................4.
1.2. Potrzeby stanu obciążenia............................................................................................................................4.
2. Potrzeby stanu jałowego....................................................................................................................................4.
2.1. Potrzeby z upływu w liniach..........................................................................................................................4.
2.1.1. Linie napowietrzne wysokiego napięcia.....................................................................................................4.
2.1.2. Linie napowietrzne niskiego napięcia........................................................................................................6.
2.1.3. Wewnętrzne linie zasilające.......................................................................................................................9.
2.1.4. Odbiorcze instalacje wewnętrzne..............................................................................................................9.
2.2. Potrzeby z ulotu w liniach napowietrznych...................................................................................................9.
2.3. Potrzeby dielektryczne w liniach kablowych..............................................................................................15.
2.4. Potrzeby baterii kondensatorów ...............................................................................................................18.
2.5. Potrzeby innych źródeł mocy biernej ........................................................................................................18.
3. Potrzeby stanu obciążenia.............................................................................................................................19.
3.1. Zużycie energii na potrzeby własne w przewodach roboczych linii............................................................19.
3.2. Rezystancja przewodów linii.......................................................................................................................20.
3.2.1. Wpływ temperatury na rezystancję..........................................................................................................21.
3.2.2. Wpływ zjawiska naskórkowości na rezystancję.......................................................................................21.
3.2.3. Wpływ korozji przewodów........................................................................................................................22.
3.2.4. Wpływ budowy linii...................................................................................................................................23.
3.2.5. Uwagi końcowe........................................................................................................................................23.
3.3. Wyznaczenie zużycia energii na potrzeby własne zależnie od obciążenia................................................23.
3.3.1. Czas trwania maksymalnego obciążenia.................................................................................................24.
3.3.2. Czas trwania maksymalnych potrzeb......................................................................................................24.
3.4.
Obliczenie poboru mocy i zużycia energii przez przewody odgromowe na pokrycie potrzeb własnych
w liniach napowietrznych wysokich napięć. ...........................................................................................25.
-3-
3.5.
Pobór mocy
na
potrzeby
własne
uchwytów
podtrzymujących
przewody
w liniach
elektroenergetycznych.........................................................................................................................................26.
4. Moc naturalna linii..........................................................................................................................................27.
5. Literatura .......................................................................................................................................................28.
-4-
Potrzebami własnymi linii elektroenergetycznych nazywamy zużycie energii przez
przewody tych linii na skutek różnych zjawisk towarzyszących przyłożeniu napięcia i
przepływowi w nich prądu.
1. Potrzeby w liniach elektroenergetycznych dzielimy na:
-
potrzeby stanu jałowego,
-
potrzeby stanu obciążenia.
1.1. Potrzeby stanu jałowego dzielimy na:
-
potrzeby z ulotu w napowietrznych liniach elektroenergetycznych najwyższych napięć,
-
potrzeby z upływu w liniach napowietrznych niskiego i wysokiego napięcia,
-
potrzeby dielektryczne w liniach kablowych.
1.2. Potrzeby stanu obciążenia dzielimy na:
-
potrzeby w przewodach roboczych linii elektroenergetycznych,
-
potrzeby w przewodach odgromowych napowietrznych linii elektroenergetycznych,
-
potrzeby w uchwytach podtrzymujących przewody robocze.
2. Potrzeby stanu jałowego.
Potrzeby stanu jałowego głównie zależą od wartości przyłożonego napięcia oraz od izolacji rozpatrywanej
linii elektroenergetycznej.
2.1. Potrzeby z upływu w liniach.
2.1.1. Linie napowietrzne wysokiego napięcia.
Z chwilą załączenia napowietrznej linii elektroenergetycznej pod napięcie na skutek niedoskonałości
izolacji, do ziemi popłynie pewien prąd. Wielkość tego prądu, a więc i wielkość poboru energii zależy
od:
-
stanu pogody,
-
gęstości powietrza,
-
jakości izolacji,
-
zanieczyszczeń i uszkodzeń izolacji,
-
przyłożonego napięcia.
-5Jednostkowy pobór energii na potrzeby z upływu wyznaczamy ze wzoru:
∆Aupł. = U2 ⋅ ( G’ ⋅ t1 + G” ⋅ t2 ) ⋅ 10-3
[ kW⋅h / km ]
(1)
gdzie:
U [ kV ]
– napięcie międzyprzewodowe
G [ S / km ] – konduktywność
t [ godz. ]
– czas trwania stanu załączenia linii.
Przy czym literatura podaje wielkości konduktywności:
G’ ≈ 0,02 S / km – dla dobrej pogody,
G” ≈ 0,05 S / km – dla złej pogody,
Roczne czasy trwania odpowiedniej pogody wg badań przeprowadzonych dla Dolnego Śląska wynoszą:
t1 = 6900 godz. – dla dobrej pogody,
t2 = 1800 godz. – dla złej pogody.
W praktyce roczny jednostkowy pobór energii na pokrycie potrzeb z upływu możemy określać wg
wzoru:
∆Aupł. = 0,228 ⋅ U2
[ kW⋅h / km i rok ]
(2)
Należy zaznaczyć, że wielkość średniorocznych poborów mocy na potrzeby z upływu określone wg
powyższego wzoru, za wyjątkiem linii 110 kV znacznie odbiegają od wielkości uzyskanych drogą pomiarową,
a mianowicie:
Napięcie sieci
w kV
Średnioroczna moc
obliczona wg wzoru
w W / km
Średnioroczna moc
uzyskana z pomiarów
w W / km
10
2,62
11,5
110
317,0
350,0
220
1268,0
209,0
a więc konieczne są tu dodatkowe badania umożliwiające bardziej precyzyjne określanie tych wielkości.
2.1.2. Linie napowietrzne niskiego napiecia.
Podobnie z chwilą załączenia pod napięcie napowietrznej linii niskiego napięcia popłynie do ziemi pewien
prąd. Wielkość tego prądu, a więc i wielkość poboru mocy i energii zależy od:
-
przyłożonego napięcia ( Rysunki: 1; 2 ),
-6-
wilgotności względnej powietrza ( Rysunek 3 ),
-
temperatury powietrza ( Rysunek 4 ),
-
gestości powietrza.
Jednostkowy pobór mocy na potrzeby z upływu wyznaczamy ze wzoru:
∆Pupł. = 0,6 ⋅ U2 ⋅ δ ⋅ Fw ⋅ Ft ⋅ 10-6
[ W / km ]
(3)
gdzie:
U [ V ] – napięcie międzyprzewodowe,
δ
– względna gęstość powietrza,
Fw
– funkcja określająca zależność poboru mocy na upływność od wilgotności względnej
powietrza,
Ft
– funkcja określająca zależność poboru mocy na upływność od temperatury powietrza.
Względną gęstość powietrza wyznaczamy ze wzoru:
δ
0 , 385 ⋅ p
273 + t
(4)
gdzie:
t [ °C ]
– temperatura powietrza w warunkach dowolnych,
p [ mmHg ] – ciśnienie atmosferyczne.
W celu określenia średniego jednostkowego zużycia energii na potrzeby linii niskiego napięcia z upływu
przeprowadzono na terenie Dolnego Śląska pomiary wielkości mocy z upływu. Przy czym pomiary te zostały
przeprowadzone w różnych warunkach atmosferycznych i na różnych liniach niskiego napięcia. Następnie
uwzględniając wpływ poszczególnych czynników oraz czasy ich występowania w ciągu roku określono średnią
roczną wielkość poboru mocy na potrzeby upływu w wysokości:
∆Pupł.śr. = 0,048 W / km
(5)
a nie 50 W / km , jak podaje dostępna literatura.
Natomiast jednostkowe roczne zużycie energii na pokrycie potrzeb z upływu dla linii niskiego napięcia
wynosi:
∆Aupł. = 0,420 kW⋅h / km i rok
(6)
∆ Pupł. [ W / km ] na trzy fazy
-70,7
0,6
0,5
0,4
2
0,3
0,2
0,1
3
1
0
0
100
200
300
400
500
600
Napięcie fazowe [ V ]
∆ Pupł. [ W / km ] na trzy fazy
Rysunek 1.
Pobór mocy na skutek upływności w zależności od zmian napięcia.
1. Pomiar z dnia 8 maja 1973 r. temp. pow. +6 °C, wilgotność pow. 100 %.
2. Pomiar z dnia 31 stycznia 1973 r. temp. pow. +5 °C, wilgotność pow. 100 %.
3. Przebieg teoretyczny.
0,4
0,3
0,2
2
0,1
3
1
0
0
100
200
300
400
500
600
Napięcie fazowe [ V ]
Rysunek 2.
Pobór mocy na skutek upływności w zależności od zmian napięcia.
1. Pomiar z dnia 13 lutego 1973 r. temp. pow. +2 °C, wilgotność pow. 100 %.
2. Pomiar z dnia 1 marca 1973 r. temp. pow. +1 °C, wilgotność pow. 100 %.
3. Przebieg teoretyczny.
Wartość funkcji Fw
-8-
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
0
10
20
30
40
50
60
70
80
90
100
Wilgotność względna powietrza [ % ]
Wartość funkcji Ft
Rysunek 3. Wartość funkcji Fw w zależności od wilgotności względnej powietrza .
1,0
0,9
0,8
0,7
0,6
0
5
10
15
20
25
30
35
40
Temperatura powietrza [ °C ]
Rysunek 4. Wartość funkcji Ft w zależności od dodatnich temperatur otoczenia.
-9-
2.1.3. Wewnętrzne linie zasilające.
W tym przypadku, pod pojęciem wewnętrznej linii zasilającej rozumiemy odcinek linii zawarty pomiędzy
izolatorami na stojaku lub na ścianie budynku, a licznikiem służącym do określania wielkości energii pobranej
przez odbiorcę.
Na podstawie przeprowadzonych na terenie Dolnego Śląska licznych pomiarów stwierdzono, że średnia
wielkości poboru mocy na potrzeby z upływności prądu do ziemi w wewnętrznych liniach zasilających waha się zależnie od stanu wewnętrznej linii zasilającej i warunków atmosferycznych – w bardzo szerokich granicach, a
mianowicie:
∆Pupł. ≈ ( 0,02 ÷ 0,15 ) W / WLZ
(7)
co daje średnio – rocznie około:
∆Aupł.W.L.Z . = 1,00 kW⋅h / WLZ i rok
(8)
2.1.4. Odbiorcze instalacje wewnętrzne.
Wykonując pomiary upływnosci pradu do ziemi w liniach napowietrznych niskiego napięcia mierzono
również upływność w instalacjach u odbiorców , a więc w instalacjach zalicznikowych.
Pobór mocy na pokrucie potrzeb upływności w instalacjach u odbiorców waha się w bardzo szerokich
granicach, bo aż od ( 0,1 ÷ 1,0 ) W na jedną instalację. Przy czym ciekawa wydaje się być następująca
prawidłowość,że w nowych instalacjach upływność jest większa. Mówimy o poborze ( stracie ) mocy dlatego, że
w tym czasie gdy odbiorca nie pobiera żadnej mocy, licznik energii elektrycznej nie będzie wykazywał tego
poboru – bowiem jest to tak mała wielkość, że nie spowoduje jego rozruchu i wówczas zuzyta energia obciąża
dostawcę ( energetykę ). Określenie wielkości rocznego poboru energii przez instalację u obiorców jest bardzo
trudna tak, jak jest trudne okreslenie rocznego czasu poboru mocy przez odbiorców.
Po wielu analizach stwierdzono, że średnia wielkość zużycia energii na potrzebu z upływności na jedną
instalację odbiorczą można ocenić na około:
∆Aupł.inst. = 2,00 kW⋅h / inst. i rok
(9)
2.2. Potrzeby z ulotu w liniach napowietrznych.
Ulotem nazywamy zjawisko samodzielnego niezupełnego wyładowania skupionego, polegające na ruchu
jonów dookoła powierzchni gołych przewodów wiodących prąd.
- 10 Czynniki wpływające na wielkość potrzeb zulotu:
-
stan pogody,
-
gęstość powietrza,
-
wymiary przewodów i linii ( Rysunki: 5 i 6 ),
-
kształt i stan powierzchni przewodów,
-
przyłożone napięcie ( Rysunek 7 ).
Rysunek 5. Zależność wielkości poboru mocy od parametrów linii.
Obliczenia wykonano wg wzorów Petersona dla linii 400 kV przy nap. rob. 415 kV i dla dobrej pogody.
* skala 1 – zmienny promień ( r w [ cm ] ), stałe a i d;
* skala 2 – zmienna odległość przewodów w wiązce ( a w [ cm ] ), stałe r i d;
* skala 3 – zmienna odległość pomiędzy fazami ( d w [ m ] ), stałe r i a.
- 11 -
∆ Pul. [ kW / km ] na trzy fazy
100,0
10,0
1,0
0,1
1
2
3
4
5
6
Ilość przewodów - n
Rysunek 6. Zależność wielkości poboru mocy od ilości przewodów w wiązce jednej fazy.
Obliczenia wykonano wg wzorów Petersona dla linii 400 kV przy napięciu roboczym 415 kV i przy dobrej
pogodzie zakładając, że: r = 1,395 [ cm ] ; a = 40,0 [ cm ] i d = 1298,0 [ cm ].
∆ Pul. [ kW / km ] na trzy fazy
1000,0
100,0
10,0
1,0
0,1
300
325
350
375
400
425
450
475
500
525
550
Ilość przewodów - n
Napięcie [ kV ]
Rysunek 7. Zależność wielkości zużycia mocy powstałej na skutek ulotu od zmian napięcia roboczego linii.
Obliczenia przeprowadzono wg wzorów Petersona dla linii 400 kV wykonanej z przewodów wiązkowych
2 ⋅ 400 AFL i dla dobrej pogody.
- 12 Zgodnie z ocenami wielu autorów najbardziej zbliżone do pomiarów doświadczalnych wielkości potrzeb z
ulotu uzyskuje się określając je wg metody opracowanej przez Petersona, wykorzystując następujące wzory:
-
dla linii wykonanej z przewodów pojedynczych:
2
3 , 49 ⋅ U
∆P ul
4
 d 
 r 


10 ⋅  log 
-
2
⋅F
[ kW / km ]
( 10 )
[ kW / km ]
( 11 )
dla linii z przewodami wiązkowymi:
2
3 , 49 ⋅ U
∆P ul
4


 d 
 rn  
2
⋅F
10 ⋅  log 
gdzie:
U [ kV ] – napięcie międzyprzewodowe linii,
d [ cm ] – średnia geometryczna odległość pomiędzy przewodami lub wiązkami przewodów różnych
faz tej samej linii – określamy ją wg zależności:
3
d
d12 ⋅ d 23 ⋅ d31
( 12 )
cyfry: 1, 2, 3 – oznaczają kolejne fazy rozpatrywanej linii,
r [ cm ] – promień przewodu rozpatrywanej linii,
rn [ cm ] – promień zastępczy wiązki przewodów w jednej fazie linii – określamy go wg zależności:
rn
n
r ⋅ (γ ⋅ a )
n− 1
( 13 )
we wzorze tym:
n
– ilość przewodów we wiązce,
a [ cm ] – odstęp pomiędzy przewodami we wiązce,
γ
– współczynnik podany w załączonej tablicy.
Ιlość przewodów w wiązce jednej fazy n
2
3
4
5
6
Współczynnik γ
1,00
1,00
1,12
1,27
1,44
- 13 -
 U
 Uj 
F=ƒ 
– a więc jest to funkcja określająca stosunek napiecia roboczego do
napięcia jonizacji ( Rysunek 8 ),
Uj [ kV ]
– międzyprzewowdowe napięcie jonizacji linii,
Skuteczną wartość międzyprzewodowego napięcia jonizacji obliczamy ze wzoru:
-
dla liniii z przewodami pojedynczymi:
d
Uj = 84,145 ⋅ m1 ⋅ m2 ⋅ m3 ⋅ δ2/3 ⋅ r ⋅log  
r
-
[ kV ]
( 14 )
dla linii z przewodami wiązkowymi:
Uj = 84,145 ⋅ m1 ⋅ m2 ⋅ m3 ⋅ m4 ⋅ δ2/3 ⋅ r ⋅ n ⋅log  d 
r
[ kV ]
( 15 )
Obliczając napięcie jonizacji dla różnych stanów pogody wzory podstawowe nie ulegają zmianie – zmieniają się
jedynie odpowiednie współczynniki.
gdzie:
m1 – współczynnik uwzględniający wpływ stanu powierzchni przewodów ( dla celów praktycznych
obliczeń przyjmuje się: 0,7 ÷ 0,9 ),
m2 – współczynnik uwzględniający wpływ stanu pogody, przyjmuje się:
1,0 – dla dobrej pogody,
0,8 – dla złej pogody,
m3 – współczynnik uwzględniający budowę przewodu, przyjmuje się około: 0,7 ,
m4 – współczynnik uwzględniający wpływ ilości przewodów we wiązce, przyjmuje się: 0,9 ,
δ
– względna gęstość powietrza.
Względną gęstość powietrza wyznaczamy ze wzoru:
δ
0 , 385 ⋅ p
273 + t
gdzie:
t [ °C ]
– temperatura powietrza w warunkach dowolnych,
p [ mmHg ] – ciśnienie atmosferyczne.
( 16 )
- 14 -
Rysunek 8. Wartość funkcji F w zależności od stosunku napięcia roboczego do napięcia jonizacji
wg Petersona.
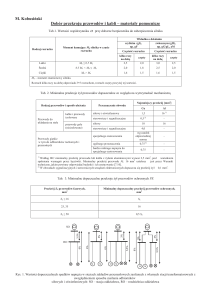
- 15 Tablica 1.
Jednostkowy średnioroczny pobór mocy na ulot.
L.p.
Wyszczególnienie
Napięcie linii
w kV
1
Jednostkowa moc
Jednostkowa moc
pobrana na ulot
pobrana na ulot przy
przy złej pogodzie
dobrej pogodzie
w kW / km
w kW / km
Średnioroczna
jednostkowa moc
pobrana na ulot
w kW / km
110,0
0,021
0,087
0,035
118,0
0,034
0,175
0,063
3
125,0
0,055
0,421
0,131
4
220,0
0,238
2,851
0,779
235,0
0,407
7,594
1,894
6
250,0
0,921
12,890
3,397
7
400,0
2,798
48,121
12,175
415,0
4,788
58,050
15,808
430,0
8,352
70,670
21,245
Linia 110 kV
2
Linia 220 kV
5
Linia 400 kV
8
9
2.3. Potrzeby dielektryczne w liniach kablowych.
Pobrana energia czynna przez linię kablową prądu przezmiennego na pokrycie potrzeb wynikających z
niedoskonałości izolacji i histerezy dielektrycznej nazywamy potrzebami dielektrycznymi. Energia ta zamienia
się na ciepło i podwyższa temperaturę izolacji kabla.
Potrzeby dielektryczne zależą od:
-
przyłożonego napięcia,
-
częstotliwości,
-
pojemności roboczej,
-
intensywności wewętrznej jonizacji.
Jednostkowy pobór mocy na potrzeby dielektryczne wyznaczamy ze wzoru:
∆P’diel. = Qc ⋅ tgδ
[ kW / km ]
( 17 )
- 16 gdzie:
Qc [ kvar / km ] - jednostkowa moc ładowania trójfazowej linii kablowej,
tgδ
- współczynnik stratności dielektrycznej, jest to tangens kąta ( δ ) dopełniającego
do 90 ° kąt ( ϕ ) przesunięcia fazowego pomiędzy prądem a napięciem, to znaczy,
że w idealnym dielektryku kąt ( ϕ ) powinien się równać 90 ° i wówczas stratność
byłaby równa zeru, czyli im gorszy dielektryk, tym większy kąt ( δ ), a więc i tgδ.
Zwykle tgδ w zależności od napięcia znamionowego kabla mieści się w granicach: 0,005 ÷ 0,022 , im wyższe
napięcie, tym mniejszy tgδ.
Natomiast dla trójfazowych – czteroprzewodowych kabli niskiego napięcia można przyjmować wartość
potrzeb dielektrycznych równą:
∆Pdiel. = ( 1,5 ÷ 2,5 ) kW⋅h / km i rok
( 18 )
3. Potrzeby stanu obciążenia.
Potrzeby stanu obciążenia zależą od wartości ( w kwadracie ) przepływającego prądu – a to oznacza, że
jeżeli rozpatrywaną linią nie będzie przesyłana żadna moc, to potrzeby nie wystąpią – oraz przekroju i materiału
z jakiego zostały wykonane przewody linii.
3.1. Zużycie energii na potrzeby własne w przewodach roboczych linii.
Pobór mocy czynnej na pokrycie potrzeb zależnych od obciążenia w przewodzie roboczym linii
elektroenergetycznej określamy wg zależności:
∆P = Ι 2 ⋅ R
[W]
( 19 )
zaś zużycie energii wg zależności:
∆A = ∆P ⋅ τ = Ι 2 ⋅ R ⋅ 10 -3
[ kW⋅h ]
( 20 )
Dla linii trójfazowej czteroprzewodowej potrzeby zależne od obciążenia stanowią:
∆P = Ι12 ⋅ R1 + Ι22 ⋅ R2 + Ι32 ⋅ R3 + Ι02 ⋅ R0
[W]
( 21 )
W przypadku, gdy przewody fazowe będą wykonane z przewodów o tym samym materiale i przekroju:
∆P = ( Ι12 + Ι22 + Ι32 ) ⋅ R + Ι02 ⋅ R0
[W]
( 22 )
- 17 Tablica 2.
Moce generowane przez kable produkcji krajowej wg Danych Bydgoskiej Fabryki Kabli z lat 90 - tych.
Napięcie Uf / U w kV
L.p.
Przekrój żył kabla
w mm2
6 / 10
8,7 / 15
12 / 20
18 / 30
Moc generowana w kvar / km
1
50
8,46
14,88
24,48
42,66
2
70
9,54
16,44
27,00
45,90
3
95
10,44
18,53
29,88
51,84
4
120
11,52
19,31
31,32
53,00
5
150
12,60
20,62
33,84
57,78
6
185
13,50
22,71
36,72
61,02
7
240
14,94
25,06
40,68
66,96
8
300
16,20
26,88
43,56
73,44
9
400
18,54
30,54
48,96
82,62
10
500
20,34
33,41
52,00
88,56
11
630
22,32
37,06
59,76
97,74
12
800
25,02
42,02
66,60
106,92
13
1000
27,72
45,68
73,08
116,40
- 18 Tablica 3.
Moce generowane ( pojemnościowe ) przez linie napowietrzne średnich napięć.
Napięcie linii w kV
Przekrój
L.p.
przewodu
AFL w mm2
10
15
20
30
Moc generowana w kvar / km
1
25
0,287
0,646
1,110
2,497
2
35
0,296
0,666
1,143
2,571
3
50
0,305
0,686
1,175
2,644
4
70
0,313
0,705
1,207
2,702
5
95
0,323
0,728
1,244
2,799
6
120
0,333
0,745
1,280
2,881
7
150
0,339
0,746
1,304
2,933
Tablica 4.
Moce generowane ( pojemnościowe ) przez linie napowietrzne o napięciu 110 kV .
L.p.
Przekrój przewodu AFL w mm2
Moc generowana w kvar / km
1
95
32,153
2
120
32,786
3
150
33,153
4
185
33,848
5
240
34,562
6
300
35,123
- 19 Tablica 5.
Moce generowane ( pojemnościowe ) przez linie napowietrzne o napięciu 220 kV .
L.p.
Przekrój przewodu AFL w mm2
Moc generowana w kvar / km
1
185
127,534
2
240
129,736
3
300
132,132
4
350
133,729
5
400
135,133
6
525
138,472
7
675
140,892
Tablica 6.
Moce generowane ( pojemnościowe ) przez linie napowietrzne o napięciu 400 kV .
L.p.
Przekrój przewodu AFL w
Moc generowana w kvar / km
2
mm
Przewody pojedyncze
przewody podwójne
1
350
409,120
542,560
2
400
409,600
542,880
3
525
416,960
549,280
4
675
425,440
556,640
- 20 zaś w przypadku, gdy przewody fazowe i zerowy są o takim samym przekroju i z takiego samego materiału to:
∆P = ( Ι12 + Ι22 + Ι32 + Ι02 ) ⋅ R
[W]
( 30 )
W przypadku linii trójfazowej trójprzewodowej, zależność będzie następująca:
∆P = ( Ι12 + Ι22 + Ι32 ) ⋅ R
[W]
( 31 )
rozpatrując linię trójfazową trójprzewodową obciążoną symetrycznie ( zwykle będzie to linia wysokiego
napięcia ) – otrzymamy:
∆P = 3 ⋅ Ι2 ⋅ R
[W]
( 32 )
Natomiast zużycie energii na pokrycie potrzeb własnych linii określamy wg zależności:
∆A = ∆P ⋅ τ = 3 ⋅ Ι 2 ⋅ R ⋅ τ
[ W⋅h ]
( 33 )
gdzie:
∆A [ W⋅h ] - zużycie energii czynnej na pokrycie potrzeb własnych,
∆P [ W ]
- pobór mocy czynnej na potrzeby własne,
Ι
[A]
- prąd płynący w przewodach linii,
R
[Ω]
- rezystancja przewodów linii,
τ
[h]
- czas trwania maksymalnych potrzeb.
3.2. Rezystancja przewodów linii.
Rezystancja przewodów linii przy przepływie prądu zależy od materiału, przekroju poprzecznego i
długości przewodu.
Rezystancję jednostkowa przewodu określamy z zależności:
Ro
1000
γ ⋅S
[ Ω / km ]
gdzie:
Ro [ Ω / km ] - rezystancja jednostkowa przewodu,
S
γ
[ mm2 ]
- rzeczywisty przekrój poprzeczny przewodu,
m
Ω ⋅ mm
2
- konduktancja jednostkowa przewodu.
( 34 )
- 21 W praktyce jednak nie zaleca się wykonywania obliczenia rezystancji jednostkowej przewodów wg
podanej metody, lecz korzystać z wartości rezystancji jednostkowych podanych w tablicach ( publikowanych w
różnych kalendarzykach czy katalogach ).
Dodatkowo zwracam uwagę, że wartości rezystancji jednostkowej podawane w tablicach są określane
dla prądu stałego i temperatury +20 °C.
Tak więc określając rezystancję dla całego przewodu linii postępujemy w sposób następujący:
R = Ro ⋅ 
[Ω]
( 35 )
gdzie:
R [ Ω ] - rezystancja całego przewodu,
 [ km ] - długość przewodu.
Zwracam uwagę, że wykonując obliczenia potrzeb powodowanych przepływem prądu przemiennego w
przewodach linii elektroenergetycznych wskazane jest uwzględnienie dodatkowych czynników wpływających na
zmiany rezystancji przewodów. Do czynników wpływających na zmiany rezystancji przewodów przy przepływie
prądu przemiennego należą:
-
temperatura,
-
naskórkowość,
-
korozja przewodu,
-
wpływ budowy linii,
-
wpływ wyższych harmonicznych.
3.2.1. Wpływ temperatury na rezystancję.
Przy przyroście temperatury przewodów miedzianych , aluminiowych czy stalowo – aluminiowych
następuje przyrost rezystacji tych przewodów po około 0,4 % na jeden stopień przyrostu ich temperatury ,
natomiast przy zmniejszaniu temperatury – zmniejsza się ich rezystancja. Dla przykładu podaję, że dla
przewodów w przekroju 840 AFL , graniczna dopuszczalna temperatura wynosi +80 °C , a więc różnica
pomiędzy temperaturami wynosi 60 °C. I w tym przypadku rezystancja przewodów wzrośnie aż o 24 %.
3.2.2. Wpływ zjawiska naskórkowości na rezystancję.
Przy przepływie prądu stałego gęstość prądu w poprzecznym przekroju przewodu jest równomierna, to
znaczy, że ma tą samą wartość we wszystkich punktach przekroju. Natomiast przy przepływie prądu przemien -
- 22 nego, wytwarza się wewnątrz przewodu zmienne pole magnetyczne, które powoduje nierównomierny rozkład
gęstośći prądu w poprzecznym przekroju przewodu, a mianowicie gęstość prądu zwiększa się w kierunku od osi
przewodu do jego powierzchni. Przy czym przyrost gęstości prądu jest tym większy, im większa jest
częstotliwość prądu i im większa jest przenikalność magnetyczna materiału oraz przekrój poprzeczny przewodu
– zjawisko to nazywamy naskórkowością.
Naskórkowość wyraża się zależnością:
k
Rop
( 36 )
Ros
gdzie:
Rop [ Ω / km ] – jednostkowa rezystancja przy przepływie prądu przemiennego,
Ros [ Ω / km ] – jednostkowa rezystancja przy przepływie prądu stałego,
k
– współczynnik naskórkowości lub współczynnik przyrostu rezystancji przewodu.
Dodatkowo zaznaczam, że przyrost rezystancji przewodu przy przepływie prądu przemiennego
powodowany zjawiskiem naskórkowości maleje wraz ze wzrostem temperatury i rośnie wraz ze zmniejszaniem
temperatury przewodu. Jeżeli chodzi o wartości przyrostu rezystancji na skutek zjawiska naskórkowości, to
waha się ona od 0,064 % - dla przekroju przewodu 120 AFL do 3,570 % - dla przekroju przewodu 840 AFL .
Natomiast zmniejszenie temperatury przewodu o 60 °C ( za podstawę przyjęto: +20 °C ) do temperatury:
-40 °C - powoduje zwiększenie przyrostu rezystancji o około 16,0 %, a przy zwiększeniu temperatury przewodu
o 60 °C do temperatury +80 °C - powoduje zmniejszenie przyrostu rezystancji o około 50 %.
Należy jednak zaznaczyć, że o ile naskórkowość powoduje niezbyt duży przyrost rezystancji przewodów
linii elektroenergetycznych, to powoduje duże przyrosty stanu obciążenia szczególnie w transformatorach
dużych lub bardzo dużych mocy.
3.2.3. Wpływ korozji przewodów.
Przewody linii napowietrznych narażone są na korozję, co oczywiście powoduje przyrost ich rezystancji.
Przy czym zwracam uwagę, że przyrost rezystancji waha się w bardzo szerokich granicach i zależy od wielu
czynników, a mianowicie:
-
budowa przewodu – przewody AFL ,
-
wiek linii,
- 23 -
atmosfera, a zwłaszcza agresywna pod względem chemicznym.
W wyniku przeprowadzonych wielu badań różnych linii o niejednakowym okresie eksploatacji,
stwierdzono, że przyrost rezystancji na skutek korozji waha się średnio: ( 8 ÷ 10 ) %.
3.2.4. Wpływ budowy linii.
Określając wartość rezystancji linii elektroenergetycznych zwykle dysponujemy długością tej linii, a nie
długością przewodów prąd wiodących, dlatego też należy pamiętać o uwzględnieniu przyrostu rezystancji , a
mianowicie:
-
dla linii napowietrznych niskiego napięcia, zwiększyć o około: 0,2 % ,
-
dla linii napowietrznych wysokiego napięcia, zwiększyć o około: 0,5 % ,
-
dla linii kablowych, zwiększyć o około: 0,3 % .
3.2.5. Uwagi końcowe.
Z przeprowadzonych rozważań wynika, że w zasadzie wszystkie omówione zjawiska zachodzące przy
przepływie prądu przemiennego powodują przyrosty rezystancji przewodów – dlatego też wykonyje się
wykonując obliczenia potrzeb zależnych od obciążenia, należy uzyskany wynik powiększyć o około 10,0 %.
3.3. Wyznaczenie zużycia energii na potrzeby własne zależnie od obciążenia.
Rozpatrując przebiegi obciążenia linii, rozdzielni, rejonu czy zakładu elektroenergetycznego, możemy
wyróżnić następujące pojęcia:
-
moc maksymalna ( Pmax ),
-
moc minimalna ( Pmin ),
-
energia wprowadzona,
-
moc średnia ( Pśr ).
Definicje.
Mocą maksymalną ( Pmax ) nazywamy największą moc, jaka została wprowadzona do systemu w
rozpatrywanym okresie czasu.
Mocą minimalną ( Pmin ) nazywamy najmniejszą moc, jaka została wprowadzona do systemu w
rozpatrywanym okresie czasu.
- 24 Energią wprowadzoną lub zużytą w czasie ,, t ‘’ wyrażamy:
⌠t
 P t dt
⌡0
A
[ W⋅h ]
( 37 )
a więc jest to pole powierzchni ograniczone krzywą przebiegu obciążenia i czasem trwania tego przebiegu,
gdzie:
Pt [ W ]
t
- moc chwilowa,
[ godz. ] - czas trwania poboru mocy.
Mocą średnią ( Pśr ) nazywamy moc niezmieniającą się w czasie, przy której do systemu została
wprowadzona taka sama ilość energii elektrycznej, jak przy rzeczywistym przebiegu w rozpatrywanym okresie
czasu, a więc:
Psr
A
t
[W]
( 38 )
3.3.1. Czas trwania maksymalnego obciążenia.
Czasem trwania maksymalnego obciążenia nazywamy czas, przy którym wprowadzając do systemu
elektroenergetycznego moc maksymalną, wprowadzona zostanie taka sama ilość energii elektrycznej, jak przy
rzeczywistym przebiegu obciążenia i w rzeczywistym okresie czasu, a więc:
T
A
Pmax
[ godz. ]
( 39 )
( jest to przebieg prostokątny ).
3.3.2. Czas trwania maksymalnych potrzeb.
Czasem trwania maksymalnych potrzeb nazywamy czas, w którym przepływający maksymalny prąd
powoduje takie same zużycie energii, jak przy rzeczywistym przebiegu obciążenia i w rzeczywistym okresie
czasu, a więc:
τ
∆A
∆P max
[ godz. ]
( 40 )
Czas trwania maksymalnych potrzeb określamy wg wzoru empirycznego ( doświadczalnego ):
τ
T 
T
⋅ 1 + 2 ⋅
3 
t 
[ godz. ]
( 41 )
- 25 -
3.4. Obliczenie poboru mocy i zużycia energii przez przewody odgromowe
na pokrycie potrzeb własnych w liniach napowietrznych wysokich napięć.
Zużycie własne przewodów odgromowych linii napowietrznych powstaje na skutek przepływu w nich
prądu, wywołanego przez siłę elektormotoryczną pochodzącą od prądu płynącego w przewodach roboczych
linii.
Jednostkowe zużycie mocy w przewodzie odgromowym obliczamy zgodnie z zależnością:
∆Po = Ιo2 ⋅ Ro
[ W / km ]
( 42 )
gdzie:
Ιo [ A ]
- prąd w przewodzie odgromowym,
Ro [ Ω / km ] - rezystancja jednostkowa przewodu odgromowego.
Jednostkowe zużycie energii w przewodach odgromowych określamy wg zależności:
∆Ao = ∆Po ⋅ τ
[ W⋅h / km ]
( 43 )
Wykonując obliczenia potrzeb w przyrządach odgromowych linii elektroenergetycznych postępujemy w
sposób następujący:
-
dla linii elektroenergetycznych z jednym przewodem odgromowym – rozpatrujemy jeden obwód,
-
dla linii elektroenergetycznych z dwoma przewodami odgromowymi – rozpatrujemy dwa obwody.
Po przeprowadzeniu szeregu analiz potrzeb przewodów odgromowych na różnych typach linii
jednotorowych i dwutorowych, przedstawiam następujące wnioski:
a) Zastępując przewody odgromowe wykonane z linek stalowo – aluminiowych, przewodami stalowymi
o tym samym przekroju – możemy uzyskać nawet wielokrotne zmniejszenie potrzeb.
b) Stwierdzono również, że udziały procentowe potrzeb w przewodach odgromowych w stosunku do
potrzeb w przewodach roboczych stanowi:
-
dla linii 110 kV: 0,26 %,
-
dla linii 220 kV: 0,86 %,
-
dla linii 400 kV: 4,39 %.
Zaznaczam, że stosunek ten jest stały i nie zależy od obciążenia linii.
- 26 c) Natomiast średnie jednostkowe wartości potrzeb w przewodach odgromowych napowietrznych linii
elektroenergetycznych obciążonych mocą naturalną w przybliżeniu stanowią:
dla linii 110 kV: 40 W / km
( 44 )
dla linii 220 kV: 200 W / km
( 45 )
dla linii 400 kV: 1800 W / km
( 46 )
3.5. Pobór mocy na potrzeby własne uchwytów podtrzymujących przewody
w liniach elektroenergetycznych.
Płynący prąd przemienny w przewodach linii napowietrznych wywołuje powstanie wokół tych przewodów
pola elektromagnetycznego. Pole to powoduje grzanie się - na skutek wystąpienia prądów wirowych - uchwytów
podtrzymujących przewody robocze linii, to oznacza, że jeżeli uchwyty te będą wykonane z materiałów
ferromagnetycznych, wystąpi zużycie pewnej ilości energii elektrycznej ( potrzeby własne uchwytów ).
Natomiast, jeżeli uchwyty będą wykonane z materiałów nie magnetycznych - potrzeby prawie nie wystąpią ( są
pomijalne ). Analizując wartości potrzeb w uchwytach dla różnych potrzeb linii napowietrznych wysokich napięć
stwierdzono, że:
a) Udziały procentowe potrzeb w uchwytach w stosunku do potrzeb w przewodach roboczych stanowi:
-
dla linii 110 kV: 0,32 %,
-
dla linii 220 kV: 0,81 %,
-
dla linii 400 kV: 1,20 %.
Podobnie i w tym przypadku stosunek ten jest stały i nie zależy od obciążenia linii.
b) Zaś średnie jednostkowe wartości potrzeb w uchwytach podtrzymujących przewody robocze linii
obciążonych mocą naturalną w przybliżeniu stanowią:
dla linii 110 kV: 50 W / km
( 47 )
dla linii 220 kV: 140 W / km
( 48 )
dla linii 400 kV: 450 W / km
( 49 )
Reasumując powyższe analizy należy stwierdzić, że zarówno potrzeby przewodów odgromowych, jak i
uchwytów są na tyle małe, że w praktycznych obliczeniach potrzeb zależnych od obciążenia przewodów
roboczych linii elektroenergetycznych są pomijalne.
- 27 -
4. Moc naturalna linii.
Każda linia elektroenergetyczna będąca pod napięciem wytwarza pewną moc bierną pojemnościową
( moc ładowania ), a przy przesyle mocy ,, pobiera ‘’ pewną moc bierną indukcyjną ( zużycie mocy biernej
indukcyjnej ). Wobec tego może zaistnieć taki przypadek moc bierna ( pojemnościowa ) wytworzona będzie się
równała mocy biernej ( indukcyjnej ) pobranej przez linię i wówczas otrzymamy zależność:
Ι2 ⋅ ω ⋅ L = U2 ⋅ ω ⋅ C
( 50 )
dla linii trójfazowej:
3 ⋅ Ι 2 ⋅ ω ⋅ L = U2 ⋅ ω ⋅ C
( 51 )
gdzie:
U [ V ] - napięcie międzyprzewodowe.
Gdy zależność ta zostanie spełniona – linia prądu przemiennego zachowa się tak, jak linia prądu stałego
– a to znaczy, że wystąpi w niej tylko pobór mocy czynnej, a moc, przy której to wystąpi nazywamy mocą
naturalną linii, którą określa zależność:
2
PN
U
Zf
[ kW lub kV⋅A ]
( 52 )
gdzie:
Zf [ Ω ] - impedancja falowa linii ( dla linii napowietrznych Zf = 50 Ω , a dla linii kablowych Zf = 400 Ω ).
Najczęściej dla obliczenia mocy naturalnej linii są spotykane następujące zależności:
-
-
dla linii napowietrznych:
PN = 2,5 ⋅ U 2
[ kW lub kV⋅A ] – jeden przewód we fazie
( 53 )
PN = 3,2 ⋅ U 2
[ kW lub kV⋅A ] – dwa przewody we fazie
( 54 )
dla linii kablowych:
PN = 20,0 ⋅ U 2
[ kW lub kV⋅A ]
( 55 )
Z powyższego rozważania wynika, że moc naturalna linii elektroenergetycznej zależy tylko od
znamionowego napięcia, natomiast nie zależy ani od długości linii ani od jej przekroju.
- 28 -
5. Literatura.
1. Potrzeby własne linii elektroenergetycznych
M. Konstanciak – 1995 r.
2. Obliczanie potrzeb własnych oraz ocena sprawności sieci elektroenergetycznych.
M. Konstanciak – 1996 r.
3. Kompensacja mocy i energii biernej w sieciach elektroenergetycznych.
M. Konstanciak – 1999 r.
4. Wykonywanie bilansów energii czynnej i biernej oraz ocena potrzeb w obszarach sieciowych.
M. Konstanciak – 2001 r.