Cwiczenie 12

8
ĆWICZENIE NR
POMIAR REZYSTANCJI MOSTKIEM
THOMSONA
11.1. Cel ćwiczenia
Celem ćwiczenia jest poznanie zasady i właściwości pomiaru rezystancji
mostkiem Thomsona.
11.2. Podstawy teoretyczne pomiaru
11.2.1. Zasada pomiaru mostkiem Thomsona
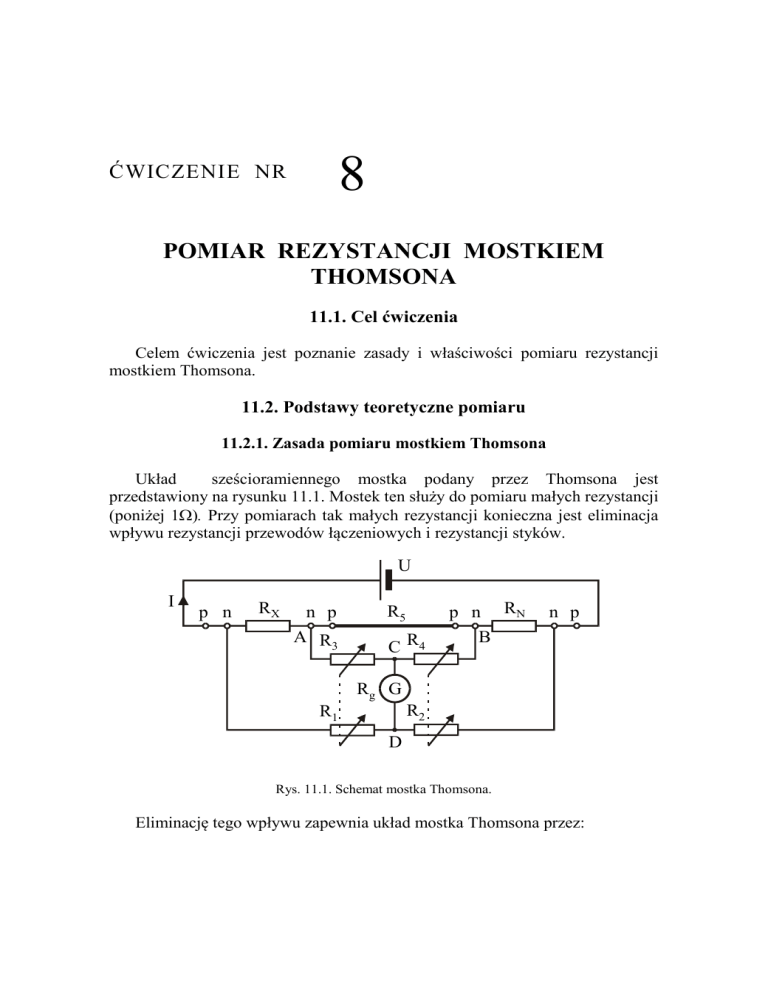
Układ
sześcioramiennego mostka podany przez Thomsona jest
przedstawiony na rysunku 11.1. Mostek ten służy do pomiaru małych rezystancji
(poniżej 1). Przy pomiarach tak małych rezystancji konieczna jest eliminacja
wpływu rezystancji przewodów łączeniowych i rezystancji styków.
U
I
p n
RX
n p
A R3
R5
C R4
Rg G
R1
p n RN
B
n p
R2
D
Rys. 11.1. Schemat mostka Thomsona.
Eliminację tego wpływu zapewnia układ mostka Thomsona przez:
169
- zastosowanie rezystorów stosunkowych R3 i R4 mechanicznie sprzężonych
odpowiednio z rezystorami R1 i R2,
- dobór wartości rezystancji R1, R2, R3, i R4, tak dużych (większych od 10), że
można pominąć rezystancje przewodów łączących.
Przez rezystancję R5 oznaczono sumę rezystancji styków i przewodów łączących
punkty A i B. Wskaźnikiem równowagi jest galwanometr magnetoelektryczny G
o rezystancji Rg. Mostek jest zasilany ze źródła o napięciu U.
Stanem równowagi mostka nazywa się taki stan, w którym napięcie między
punktami C i D jest równe zeru, przy niezerowej wartości prądu zasilającego
mostek.
Analizę działania i ocenę właściwości mostka można uprościć przez
przekształcenie układu sześcioramiennego w układ czteroramienny. W tym celu
trójkąt ABC, utworzony przez rezystory R3, R4,i R5, zastępuje się równoważną
gwiazdą o rezystorach R6, R7 i R8.
U
RX
R6
R7
RN
R8
R1
G Rg
R2
Rys. 11.2. Schemat zastępczy mostka Thomsona
Wartości rezystancji R6, R7,R8 oblicza się ze wzorów (11.1)
R6 
R5  R3
R3  R 4  R5
R7 
R5  R 4
R3  R 4  R5
R8 
R3  R 4
R3  R 4  R5
(11.1)
170
Dla stanu równowagi mostka słuszne są zależności (11.2) i (11.3)
I1  I2 ,
I3  I4
I 1 R x  R6   I 3  R1
I 2  R N  R7   I 4  R 2
(11.2)
(11.3)
Dzieląc stronami równania (11.3) i uwzględniając zależności (11.2)
otrzymuje się warunek równowagi mostka o schemacie zastępczym
przedstawionym na rysunku 11.2.
Rx  R6
R
 1
RN  R7
R2
(11.4)
Z warunku równowagi mostka, po uwzględnieniu zależności (11.1),
wyznacza się wartość rezystancji mierzonej Rx
Rx  R N
 R1
R 
R1
R4

 R5
 3
R2
R3  R4  R5  R2
R4 
(11.5)
Ponieważ, w budowanych mostkach zwykle wykonuje się R1 = R3 oraz
R2 = R4 ( jednoczesna regulacja odpowiednich rezystorów), to wówczas
rezystancję Rx oblicza się według wzoru
Rx  R N
R1
R2
(11.6)
Przy bardzo dokładnych pomiarach należy korzystać ze wzoru (11.5)
ponieważ rezystory R1, R2, R3 i R4 są wykonywane z określoną dokładnością i
założenie jednakowych wartości rezystancji R1 i R3 oraz R2 i R4 może nie być
spełnione. Należy przy tym zauważyć, że im mniejsza jest wartość rezystancji
R5, tym mniejsza jest różnica między wartościami rezystancji obliczanymi z
wzorów (11.6) i (11.7). W celu zmniejszenia R5 , punkty A, B łączy się
przewodem o bardzo małej rezystancji.
171
11.2.2. Dokładność pomiaru mostkiem Thomsona
Przyczyny powstawania błędów przy pomiarach rezystancji mostkiem
Thomsona są następujące:
- ograniczona dokładność wykonania rezystorów mostka, a w szczególności
trudność zachowania R1 = R3 i R2 = R4,
- niedostateczna czułość galwanometru,
- siły termoelektryczne,
- skończona wartość rezystancji R5,
- zmiany rezystancji gałęzi mostka wskutek zmian ich temperatury.
Ograniczona dokładność wykonania rezystancyjnych elementów mostka jest
źródłem błędów pomiaru mostkiem B. Względną wartość tego błędu określa
zależność




R5
    RN   R3   R4 
 R1   R2   R3   R4  (11.7)
Rx  RN


R
max
gdzie:
 R ,  R , ... R
N
1
4
- względne wartości błędów granicznych odpowiednich
rezystorów.
Przy pomiarach metodą zerową należy liczyć się z błędem czułości.
Bezwzględny błąd czułości jest to taka zmiana rezystancji mierzonej Rx w
zrównoważonym mostku, która powoduje zauważalne odchylenie  organu
ruchomego galwanometru (w praktyce   0,1dz ). Przybliżoną wartość
względnego błędu czułości  cz można obliczyć z wzoru (11.8).
 cz 
R 
x 0 ,1dz
Rx

 1
ci R1 
1 


2  Rg 
10 Iz Rx 
R1 R2  



(11.8)
gdzie:
ci - stała prądowa galwanometru,
Rg - rezystancja wewnętrzna galwanometru,
Rx  0,1dz - zmiana rezystancji Rx powodująca odchylenie  równe 0,1dz ,
Iz - natężenie prądu zasilającego mostek.
172
Z wzoru (11.8) wynika, że aby uzyskać mały błąd czułości, należy
zastosować odpowiednio czuły wskaźnik równowagi o małej wartości
rezystancji wewnętrznej Rg , zasilać mostek prądem Iz o odpowiednio dużym
natężeniu oraz wybrać odpowiednie wartości rezystancji R1, R2.
Względny błąd czułości mostka można określić doświadczalnie. W tym celu
w zrównoważonym mostku należy zakłócić równowagę zmieniając rezystancję
R1 o taką wartość R1 , aby uzyskać określone odchylenie galwanometru  , a
następnie obliczyć wartość  R1  0,1dz odpowiadającą odchyleniu o 0,1 dz.
R1  0,1dz

R1
10
(11.9)
Względny błąd czułości oblicza się z zależności
 cz 
R1  0,1dz
R1
(11.10)
Na dokładność pomiaru mostkiem Thomsona mogą mieć wpływ siły
termoelektryczne powstające w miejscach połączeń przewodów z elementami
mostka. Wpływ ten eliminuje się wykonując połowę pomiarów przy jednej
biegunowości źródła, a drugą połowę przy przeciwnej. Wynik pomiaru to
średnia arytmetyczna obliczona z wyników tak przeprowadzonych pomiarów.
Zmiana temperatury powoduje zmianę rezystancji elementów mostka. Jeżeli
temperatura dowolnego rezystora nie jest określona (nie jest kontrolowana), to
jego rezystancja jest w pewnym zakresie nieokreślona.
Wpływ rezystancji R5 na dokładność pomiaru mostkiem widać wyraźnie
przy porównaniu wzorów (11.6) i (11.5) oraz analizie wyrażenia (11.7). Należy
zapewnić możliwie najmniejszą wartość rezystancji R5.
11.2.3. Dobór elementów mostka
Z punktu widzenia wymaganej dokładności pomiaru mostkiem dokonuje się
doboru:
a) wartości rezystancji w poszczególnych gałęziach mostka,
b) wskaźnika stanu równowagi,
c) wartości natężenia prądu zasilającego mostek.
173
Przy doborze wartości rezystancji w poszczególnych gałęziach mostka
należy kierować się kryterium czułości oraz ograniczeniem wpływu przewodów
łączących. Mając to na uwadze zwykle dobiera się
R1 , R3 , R4 , R2  10
oraz
(11.11)
0,1Rx  RN  10Rx
Dobór galwanometru magnetoelektrycznego polega na zastosowaniu
galwanometru o takiej czułości, aby względny błąd czułości układu mostkowego
był dziesięciokrotnie mniejszy od wartości względnego błędu systematycznego
granicznego (względny błąd czułości wyznacza się doświadczalnie - wzór
(11.10)). Rezystancja zewnętrzna krytyczna galwanometru powinna być
zbliżona do rezystancji mostka "widzianej" z punktów C i D mostka.
Wartość natężenia prądu zasilającego mostek jest ograniczona
dopuszczalnymi wartościami mocy wydzielanych na rezystorach Rx i RN.
11.3. Wykonanie ćwiczenia
11.3.1. Pomiar rezystancji technicznym mostkiem Thomsona
Układ połączeń
Rx
MT
Rys. 11.3. Układ połączeń do pomiaru rezystancji technicznym
mostkiem Thomsona.
Oznaczenia
Rx - rezystancja mierzona,
MT- techniczny mostek Thomsona.
174
Uwaga: w czasie ćwiczenia należy wpisać obok podanych oznaczeń,
określenia i wartości charakteryzujące użyte przyrządy.
Postępowanie podczas pomiaru
Za pomocą technicznego mostka Thomsona pomierzyć rezystancje dwóch
rezystorów wskazanych przez prowadzącego ćwiczenie.
Protokół wyników pomiaru
Rx1 =..... - rezystancja.....................,
Rx2 =.... - rezystancja.......................
11.3.2. Badanie czułości układu mostkowego
Układ połączeń
A
r
w
U
p
RX
G
G
R5
RX
RN
RN
MT
Rys. 11.4. Schemat połączeń do pomiaru rezystancji
za pomocą laboratoryjnego mostka Thomsona
175
Oznaczenia
G - galwanometr,
RN - opornik wzorcowy,
r - opornik suwakowy,
w - wyłącznik,
Rx - rezystancja mierzona,
p - przełącznik,
MT - laboratoryjny mostek Thomsona,
U - źródło napięcia.
Uwaga: w czasie ćwiczenia należy wpisaći obok podanych oznaczeń,
określenia i wartości charakteryzujące użyte przyrządy.
Postępowanie podczas pomiaru
W układzie połączeń przedstawionym na rysunku 11.4 zbadać czułość
układu mostkowego, mierząc rezystancję rezystora wskazanego przez
prowadzącego ćwiczenie. Wykonać pomiary dla dwóch wartości rezystorów
stosunkowych przy trzech wartościach prądu zasilającego mostek.
W warunkach określonych wartościami podanymi w tabeli zrównoważyć
mostek przez zmianę wartości rezystancji Rp. Następnie w zrównoważonym
mostku należy zmieniać wartość rezystancji Rp o wartości “+Rp” i “- Rp”
podane w tabeli i odczytać odpowiadające tym zmianom odchylenia
galwanometru “-” i +”.
Dla określenia błędu czułości obliczyć
 śr 
  
2
R p 0,1  R p
śr
Wyniki pomiarów zamieścić w tabeli 11.1.
Uwaga: Oznaczenia w tabeli 11.1 są zgodne z oznaczeniami umieszczonymi na
płycie mostka MWT-77a.
Na podstawie wyników pomiarów i obliczeń błędu czułości wybrać
najkorzystniejsze warunki pomiaru, w których zostanie przeprowadzony pomiar
w następnym punkcie ćwiczenia.
176
Protokół wyników pomiaru
Lp
1.
2.
3.
4.
5.
6.
R1  R2

1000
1000
1000
100
100
100
I
A
0,2
0,4
1,0
0,2
0,4
1,0
Rp

R p

10
10
10
1
1
1
Rx



 sr
dz
dz
dz
R 
Tabela 11.1
cz
p 0,1dz
/dz
%
Wzory i przykłady obliczeń
Układ mostkowy ma największą czułość przy
R1= R2 = ... , oraz
I = ...A.
Błąd czułości układu mostkowego w tych warunkach wynosi
 cz 
R 
p
Rp
0 ,1
.... 
11.3.3. Pomiar rezystancji Rx
Postępowanie podczas pomiarów
W układzie połączeń jak dla punktu 11.3.2. oraz w warunkach maksymalnej
czułości, wyznaczonych w tym punkcie ćwiczenia zmierzyć wartość rezystancji
Rx. Wykonać po pięć pomiarów dla obu położeń przełącznika p.
177
Protokół wyników pomiarów
R1= R2=...,
I =...A
Tabela 11.2
Lp.
R p pr
R plew
R pś r
Rix
Rx
 i Rx
 i R x 2






2
Uwaga: Rppr i Rplew - to dwie wartości dekady Rp w zrównoważonym mostku
otrzymane przy dwóch przeciwnych kierunkach prądu zasilania mostka.
Wzory i przykłady obliczeń

1
R ppr  R plew
2
R pśr
Rix  R N
R1
R pśr 

R x - średnia wartość rezystancji z pięciu pomiarów,
R xś r 
1
n
n
R
i 1
ix
 i R x  Ri x  R x
Niepewność standardowa typu A
uA 
1
 i Rx 2

nn  1
Niepewność standardowa typu B ( wynikająca z dokładności użytego
mostka) określa zależność
178
uB 
M g
3

m g  Rx
100 3
gdzie:
mg - względny błąd graniczny mostka.
Niepewność standardowa łączna
u  uA2  uB2
Niepewność całkowita
u c  k  u
Wartość zmierzonej rezystancji
R x  R xś r  u c
11.4. Uwagi o wynikach pomiarów
11.5. Literatura
[1]
[2]
Chwaleba A., Poniński M., Siedlecki A.: Metrologia elektryczna. WNT,
Warszawa 1998.
Kalus-Jęcek B., Nowicki R.: Podstawy miernictwa elektrycznego dla
elektroników . Wydawnictwo Politechniki Łódzkiej, Łódź 1995.