1
1. OPIS ZAGADNIENIA
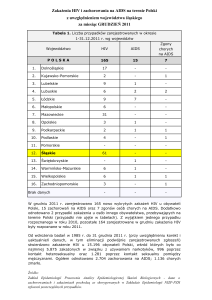
Przedmiotem projektu jest analiza liczby zachorowań na Aids w latach 1990-1996 w Polsce.
Pierwsze przypadki AIDS rozpoznano w Stanach Zjednoczonych w 1980 roku. Obecnie
AIDS ma charakter pandemii, która obejmuje swym zasięgiem wszystkie kontynenty świata.
Jeżeli utrzyma się obecne tempo rozwoju epidemii, to do końca 2000 roku liczba osób
żyjących z HIV sięgnie 40 mln.osób. W Polsce w porównaniu z innymi krajami stwierdzenie
pierwszych przypadków zachorowania na AIDS nastąpiło z kilkuletnim opóżnieniem.
Pierwsze zachorowania zarejestrowano w 1986 roku.
- Drogi szerzenia się zakażenia HIV
HIV należy do wirusów pierwotnie przenoszonych drogą seksualną (w nomenklaturze
międzynarodowej są to choroby określane skrótem STD: sexually transmitted diseases).
Zakażenie może nastąpić także przez krew i sprzęt nią skażony (niedostateczna sterylizacja), a
także od matki na płód (wewnątrzmacicznie, okołoporodowo i prawdopodobnie w związku z
karmieniem piersią).
Zakażenie w zależności od żródła:
MĘŻCZYZNI
36%
ponad 8%
narkomani
KOBIETY
53,9%
kontakty heteroseksualne
34,3%
homo- i biseksualiści
--
ok. 46 %
Poniżej zamieszczam tabelę z danymi dotyczącymi zakażeń HIV obywateli polskich,
zgłoszonych do Zakładu Epidemiologii Państwowego Zakładu Higieny w latach 1985-1994.
Grupa badanych
Zakażeni w związku z używaniem środków
odurzających
Homo i biseksualiści
Dawcy krwi
Zakażeni drogą kontaktów heteroseksualnych
Liczba
zakażeń
2270
224
173
70
Odsetek ogółu
zakażeń
69,1 %
6,8%
5,3%
2,1%
2
Chorzy na hemofilię
Osoby trudniące się prostytucją
16
14
0,5%
0,4%
Jak powszechnie wiadomo pojawienie się choroby powoduje obecność wirusa HIV w
organizmie. Im więcej nosicieli tegoż wirusa tym więcej zachorowań na AIDS .
Liczba zachorowań na AIDS jest ściśle zależna od ilości zakażeń wirusem HIV, czym
uzasadniam właśnie wybór czynników objaśniających:
-
liczba zakażonych wirusem HIV homo- i biseksualistów (na 500 przebadanych)
liczba zakażonych wirusem HIV narkomanów (na 500 przebadanych)
odsetek zarażonych wirusem HIV drogą kontaktów heteroseksualnych (na 500
przebadanych)
liczba leczonych w ośrodkach rehabilitacyjnych dla narkomanów.
Narkomani, homo- i biseksualiści oraz heteroseksualiści często zmieniający partnerów to
grupy ”największego ryzyka”. Osoby należące do tych grup są niewątpliwie najbardziej
narażone na niebezpieczeństwo zakażenia.
Również czynnik - liczba leczonych w ośrodkach rehabilitacyjnych dla narkomanów uważam,
istotnie objaśnia badane zjawisko. Tendencja rosnąca tej zmiennej nasuwa następujące
przypuszczenia : wzrastająca liczba leczonych jest skutkiem zwiększającej się ilości
narkomanów, a co za tym idzie, zwiększa się liczba potencjalnych nosicieli wirusa HIV, który
to wirus, jak już wcześniej wspomniałam, jest czynnikiem chorobotwórczym w przypadku
AIDS.
Wartości czynników objaśniających (liczba zakażonych wirusem HIV homo- i
biseksualistów, liczba zakażonych wirusem HIV narkomanów, odsetek zarażonych wirusem
HIV drogą kontaktów heteroseksualnych ) zostały przeliczone dla 500 -osobowej grupy
przebadanych w celu zapewnienia porównywalności wyników we wszystkich grupach..
Do grupy czynników objaśniających planowałam również włączyć dane o liczbie zakażeń
HIV wśród dawców krwi, osób trudniących się prostytucją i chorych na hemofilię.
Niestety wartości odnośnie danych ( chorzy na hemofilię, osoby trudniące się prostytucją) po
przeliczeniu dla 500 – osobowej grupy były zbyt małe; ich wpływ byłby znikomy dla takiej
grupy. Dane o dawcach krwi z kolei, były niekompletne we wszystkich latach co
uniemożliwiłoby prawidłowe wnioskowanie. W związku z tym danych tych nie mogłam
wykorzystać.
1.1 DANE STATYSTYCZNE:
Zmienna objaśniana Y w moim modelu to liczba zachorowań na Aids w Polsce w latach
1990-1996.
Zmienne objaśniające:
- X 1 liczba zakażonych wirusem HIV homo- i biseksualistów (na 500 przebadanych)
- X 2 liczba zakażonych wirusem HIV narkomanów (na 500 przebadanych)
3
-
Lata
X 3 odsetek zarażonych wirusem HIV drogą kontaktów heteroseksualnych (na 500
przebadanych)
X 4 liczba leczonych w ośrodkach rehabilitacyjnych dla narkomanów.
(Y)
Zachorowania
Na Aids
( X1 )
Zakażeni
wirusem HIV
homo- i
biseksualiści
/500
przebadanych
( X2 )
Zakażeni
wirusem HIV
narkomani
/500
przebadanych
( X3)
Odsetek
zarażonych HIV
drogą kontaktów
heteroseksualnych
/500
przebadanych
1990
21
28
27
0,00029
1991
35
26
25
0,00052
1992
50
22
20
0,00046
1993
68
21
15
0,0009
1994
102
33
18
0,0012
1995
114
25
24
0,0014
1996
136
41
25
0,0012
1997
167
50
48
0,0013
*dane zaczerpnięte z kwartalników ‘Przegląd epidemiologiczny’
*dane zaczerpnięte z roczników statystycznych z lat 1990-1997.
( X4 )
Liczba leczonych
w ośrodkach
rehabilitacyjnych
dla narkomanów
1088
1270
2142
1965
2027
2274
3110
3870
W tabeli umieszczam również dane z roku 1997, jednak nie wykorzystuję ich do budowy
modelu, gdyż będą mi one potrzebne do przeprowadzenia prognozy.
2. SELEKCJA CZYNNIKÓW OBJAŚNIAJĄCYCH:
Dla poszczególnych czynników objaśniających obliczam współczynniki zmienności. W
przypadku gdy wartość współczynnika danej zmiennej jest poniżej 0.1(10%), wówczas ją
odrzucam.
Korzystam z następujących wzorów:
V S / X * 100% (współczynnik zmienności)
przy czym:
X 1 n1 x
n
(średnia arytmetyczna)
2
S= 1 n1 x x (odchylenie standardowe)
n
4
Otrzymałam następujące wartości współczynników zmienności dla poszczegółnych
czynników objaśniających:
X 1 : 25%
X 2 : 20%
X 3 : 51%
X 4 : 35%
Wszystkie współczynniki mają wartość powyżej 10%, tak więc nie odrzucam żadnego
czynnika.
3. BUDOWA MODELU EKONOMETRYCZNEGO:
Budowę modelu rozpoczynam od doboru zmiennych. Do tego posłużę się procedurą StepWise-Regression pakietu STATGRAPH. Odbywa się to metodą forward lub backward (ze
stałą lub bez). Metoda forward polega na wyborze zmiennych poprzez dołączanie ich
kolejno do optymalnie wybranego zbioru. Metodą Backward natomiast, wybór zmiennych
odbywa się poprzez stopniową eliminację zmiennych z modelu.
Do badania istotności parametrów otrzymanego modelu przyjmuję współczynnik istotności
= 0.05.
METODA FORWARD:
Stepwise Selection for AIDS11.zachorow
-------------------------------------------------------------------------------Selection: Forward
Maximum steps: 500
F-to-enter: 4.00
Control: Manual
Step: 3
F-to-remove: 4.00
R-squared: .99884
Adjusted: .99768
MSE: 4.31174
d.f.: 3
Variables in Model
Coeff. F-Remove Variables Not in Model P.Corr. F-Enter
-------------------------------------------------------------------------------1. AIDS11.leczeni 0.02381 150.2229 4. AIDS11.narkoma
.6846 1.7643
2. AIDS11.shetero 60421.4 464.5258
3. AIDS11.shomo
1.03227 52.4635
Do modelu wchodzą trzy zmienne.
Model fitting results for: AIDS11.zachorow
-------------------------------------------------------------------------------Independent variable
coefficient std. error t-value sig.level
-------------------------------------------------------------------------------CONSTANT
-52.485753 3.609775 -14.5399
0.0007
AIDS11.leczeni
0.023808 0.001942 12.2565
0.0012
AIDS11.shetero
60421.368599 2803.403786 21.5529
0.0002
AIDS11.shomo
1.032266 0.142516
7.2432
0.0054
-------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9977 SE=
2.076472 MAE=
1.169095 DurbWat= 2.672
5
Previously: 0.9977
2.076472
1.169095
2.672
7 observations fitted, forecast(s) computed for 1 missing val. of dep. var.
Nie zdecydowałam się jednak na wybór tego modelu, gdyż:
-pakiet STATGRAPH wykazał aż trzy punkty wpływowe, co jest zjawiskiem
niekorzystnym, tym bardziej w moim przypadku gdy liczba lat obserwacji jest
niewielka ( 7 lat ).
Flagged Observations for AIDS11.zachorow
------------------------------------------------------------------Obs. Number Stnd. Residual Leverage Mahalanobis Dist. DFITS
3
0.90257
0.74073
13.4517
1.52559
4
-2.09694
0.37682
2.19001
-1.63059
6
2.36839
0.60136
6.70921
2.90889
------------------------------------------------------------------Number of flagged observations (residual, leverage or DFITS) = 3
-macierz korelacji obrazująca stopień skorelowania między zmiennymi była również
niesatysfakcjonująca (stopień skorelowania między zmiennymi niezależnymi był
dosyć wysoki).
Sample Correlations
-------------------------------------------------------------------------------zachorow leczeni shetero
shomo
zachorow
1.0000
.8901
.9380
.6038
( 7) ( 7) ( 7) ( 7)
.0000
.0072
.0018
.1511
leczeni
.8901 1.0000 .7147
.5206
( 7) ( 7) ( 7) ( 7)
.0072
.0000
.0711
.2309
shetero
.9380
.7147 1.0000
.4029
( 7) ( 7) ( 7) ( 7)
.0018
.0711
.0000
.3702
shomo
(
.6038
.5206
.4029 1.0000
7) ( 7) ( 7) ( 7)
.1511
.2309
.3702
.0000
-------------------------------------------------------------------------------W celu polepszenia budowanego przeze mnie modelu wartości czynnika- odsetek zarażonych
wirusem HIV drogą kontaktów heteroseksualnych na 500 osób podnoszę do kwadratu,
natomiast wartości czynnika- liczba zakażonych homo- i biseksualistów logarytmuję.
6
METODA FORWARD:
Stepwise Selection for AIDS10.zachorow
-------------------------------------------------------------------------------Selection: Forward
Maximum steps: 500
F-to-enter: 4.00
Control: Manual
Step: 3
F-to-remove: 4.00
R-squared: .99737
Adjusted: .99473
MSE: 9.80065
d.f.: 3
Variables in Model
Coeff. F-Remove Variables Not in Model P.Corr. F-Enter
-------------------------------------------------------------------------------1. AIDS10.hetero 3.05419E7 194.1027 4. AIDS10.nar
.1000 .0202
2. AIDS10.leczeni 0.03150 150.7455
3. AIDS10.homo
21.4053 11.7284
Do modelu weszły trzy zmienne.
Model fitting results for: AIDS10.zachorow
-------------------------------------------------------------------------------Independent variable
coefficient std. error t-value sig.level
-------------------------------------------------------------------------------CONSTANT
-84.309434 19.434287 -4.3382
0.0226
AIDS10.hetero
3.054193E7 2.192203E6 13.9321
0.0008
AIDS10.leczeni
0.031503 0.002566 12.2778
0.0012
AIDS10.homo
21.405307 6.250304
3.4247
0.0417
-------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9947 SE=
3.130600 MAE=
1.740210 DurbWat= 2.081
Previously: 0.9947
3.130600
1.740210
2.081
7 observations fitted, forecast(s) computed for 0 missing val. of dep. var.
METODA BACKWARD:
Stepwise Selection for AIDS10.zachorow
-------------------------------------------------------------------------------Selection: Backward
Maximum steps: 500
F-to-enter: 4.00
Control: Manual
Step: 1
F-to-remove: 4.00
R-squared: .99737
Adjusted: .99473
MSE: 9.80065
d.f.: 3
Variables in Model
Coeff. F-Remove Variables Not in Model P.Corr. F-Enter
-------------------------------------------------------------------------------2. AIDS10.leczeni 0.03150 150.7455 1. AIDS10.narkoma .7385 2.3999
3. AIDS10.hetero 3.05419E7 194.1027
4. AIDS10.homo
21.4053 11.7284
7
Model fitting results for: AIDS10.zachorow
-------------------------------------------------------------------------------Independent variable
coefficient std. error t-value sig.level
-------------------------------------------------------------------------------CONSTANT
-84.309434 19.434287 -4.3382
0.0226
AIDS10.leczeni
0.031503 0.002566 12.2778
0.0012
AIDS10.hetero
3.054193E7 2.192203E6 13.9321
0.0008
AIDS10.homo
21.405307 6.250304
3.4247
0.0417
-------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9947 SE=
3.130600 MAE=
1.740210 DurbWat= 2.081
Previously: 0.0000
0.000000
0.000000
0.000
7 observations fitted, forecast(s) computed for 0 missing val. of dep. var.
Zarówno za pomocą metody FORWARD jak i BACKWARD otrzymuję taki sam wynik.
Decyduję się na ten model.
Postać modelu:
Liczba zachor na Aids= -84.309434 + 0.031503*leczeni + 3.054193E7*hetero +
21.40530-7*homo
Y= -84.309434 + 0.031503*X4 + 3.054193E7*X3 + 21.405307*X1
Jak widać powyższy model objaśnia w 99% kształtowanie się zmiennej objaśnianej, świadczy
o tym wartość adjustowanego współczynnika determinacji R-SQ.(ADJ)=0.9947. Różni się
on nieznacznie od współczynnika determinacji R-squared, którego wartość wynosi :0.99737,
z czego wynika, że wielkość próbki nie ma wielkiego wpływu na współczynnik determinacji.
Ponadto na poziomie istotności α= 0.05 współczynniki przy zmiennych X 4 , X 3 i X 1 a także
wyraz wolny są istotne gdyż sig.level<0.05.
-współczynnik zbieżności, korelacji wielorakiej, zmienności losowej:
Współczynnik zbieżności 2 =1-R 2
2 =1-0.9947=0.0053
Oznacza to, że około 1% zmienności zmiennej objaśnianej nie zostało wyjaśnione przez
model (jest to wynikiem działania czynników przypadkowych, które nie zostały
uwzględnione w modelu).
Miarą siły związku liniowego zmiennej objaśnianej Y ze zmienną objaśniającą modelu
ekonometrycznego jest pierwiastek kwadratowy z R 2 określany mianem współczynnika
korelacji wielorakiej R.
8
W moim przypadku R=0.9973, co można uznać za satysfakcjonujące.
Współczynnik zmienności losowej We informuje jaki % średniej arytmetycznej zmiennej
objaśnianej Y modelu stanowi odchylenie standardowe reszt S e . Im mniejszy współczynnik
tym lepsze dopasowanie modelu do danych empirycznych.
S
We e
Y
W moim przypadku:
S e =2.213667
Y =75.14286
stąd:
We =2.9%
Jeżeli dla założonej z góry krytycznej wartości współczynnika zmienności losowej W * =20%
zachodzi We W * to model można uznać za dostatecznie dopasowany do danych
empirycznych.
Obliczony współczynnik zmienności losowej wynosi 2.9%, nierówność We W * zachodzi,
tak więc badany model uznaję za dostatecznie dopasowany do danych empirycznych.
4.ANALIZA OBSERWACJI:
Analizę obserwacji przeprowadzę za pomocą opcji Influence measures. Dostarcza ona
informacji o liczbie obserwacji oznaczonych (flagged) jako izolowane lub wywierające duży
wpływ na wyniki estymacji. W jej wyniku uzyskujemy następujące informacje o oznaczonych
obserwacjach: numer obserwacji (Obs. Number), studentyzowana reszta (Stnd. Residual),
miara wpływu h i (Leverage), odległość Mahalanobisa (Mahalanobis Dist.) oraz miara
wpływu DFITS (i ) (DFITS).
Flagged Observations for AIDS10.zachorow
------------------------------------------------------------------Obs. Number Stnd. Residual Leverage Mahalanobis Dist. DFITS
5
2.20638
0.36847
2.08399
1.68534
------------------------------------------------------------------Number of flagged observations (residual, leverage or DFITS) = 1
Został wykazany jeden punkt wpływowy: obserwacja o numerze 5. Właściwie powinno się
rozważyć jego usunięcie z modelu, ja jednak postanowiłam pozostawić wymieniony punkt do
dalszej obserwacji.
5. MACIERZ KORELACJI:
9
Poniżej przedstawiam macierz współczynników korelacji , którą skopiowałam z programu
STATGRAPH:
Sample Correlations
------------------------------------------------------------------------------zachorow leczeni hetero
homo
zachorow 1.0000
.8901
.9076
.5675
( 7) ( 7) ( 7) ( 7)
. 0000
.0072
.0047
.1839
leczeni
.8901 1.0000
.6378
.4511
( 7) ( 7) ( 7) ( 7)
.0072
.0000
.1233
.3096
hetero
.9076
.6378 1.0000
.4223
( 7) ( 7) ( 7) ( 7)
.0047
.1233
.0000
.3453
homo
.5675
.4511
.4223
( 7) ( 7) ( 7) (
.1839
.3096
.3453
1.0000
7)
.0000
Powyższa macierz pozwala nam określić powiązania pomiędzy zmienną objaśnianą a
zmiennymi objaśniającymi a także samymi zmiennymi objaśniającymi. Korelacje pomiędzy
zmiennymi objaśniającymi a zmienną objaśnianą są wysokie natomiast pomiędzy zmiennymi
objaśniającymi stosunkowo niskie. Jest to zjawisko korzystne.
5.1 ZASADA KOINCYDENCJI:
Model ekonometryczny posiada własność koincydencji, jeśli dla każdej zmiennej
objaśniającej znak współczynnika stojącego przy zmiennej w modelu jest równy
współczynnikowi korelacji ze zmienną objaśnianą. Oznacza to, że dla każdego i=1,...m
gdzie m-liczba zmiennych w modelu, spełniony jest warunek:
sgn bi = sgn ri
dla badanego modelu:
sgn b x 4 = sgn rx4
sgn b x 3 = sgn rx 3
sgn bx1 = sgn rx1
zatem posiada on własność koincydencji.
10
6. ANALIZA WARIANCJI :
6.1 TESTOWANIE UKŁADU WSPÓŁCZYNNIKÓW REGRESJI:
Analiza wariancji dostarcza danych dotyczących m.in. podziału całkowitej sumy kwadratów
zmiennej zależnej na część wyjaśnioną i niewyjaśnioną regresją, wartości odpowiednich
średnich kwadratów odchyleń i wartość statystyki F, która służy do weryfikacji hipotezy o
braku wpływu uwzględnionych w modelu zmiennych niezależnych na zmienną zależną.
Wartość przedstawionej analizy wygląda następująco:
.
Analysis of Variance for the Full Regression
-------------------------------------------------------------------------------------------Source
Sum of Squares DF Mean Square
F-Ratio P-value
-------------------------------------------------------------------------------------------Model
11131.5
3
3710.49
378.596 .0002
Error
29.4020
3
9.80065
-------------------------------------------------------------------------------------------Total (Corr.)
11160.9
6
R-squared = 0.997366
R-squared (Adj. for d.f.) = 0.994731
Stnd. error of est. = 3.1306
Durbin-Watson statistic = 2.08135
Z powyższych danych wynika następujący podział całkowitej sumy kwadratów odchyleń
zmiennej zależnej od średniej, która wynosi 11160.9:
-Suma kwadratów wyjaśniona za pomocą modelu: 11131.5
-Resztowa suma kwadratów: 29.4020
Odpowiednie dla obu sum kwadratów liczby stopni swobody wynoszą 3 i 3.
Średni kwadrat odchyleń resztowych (MSE), który jest oceną wariancji składnika
losowego 2 , wynosi 9.80065.
A teraz zbadam istotność wpływu wszystkich zmiennych objaśniających łącznie na zmienną
objaśnianą, czyli istotności całego wektora parametrów strukturalnych.
Stawiam następująca hipotezę zerową:
H0: a 0
wobec hipotezy alternatywnej:
H1 : a 0
gdzie a – oznacza współczynniki przy zmiennych objaśniających modelu
Sprawdzianem hipotezy H 0 jest statystyka F- Fishera-Snedecora:
F
R2 n k
1 R2 k 1
Wartość krytyczna powyższej statystyki, odczytana z tablic dla przy = 0.05 i dla
odpowiednich stopni swobody równych 3 i 3 wynosi : F*= 9.28.
11
Wartość statystyki testowej dla naszego modelu wynosi F(F-ratio)= 378.596. Ponieważ
zachodzi nierówność F F * hipotezę H 0 : a 0 należy odrzucić na rzecz hipotezy H1 : a 0 .
Oznacza to, że wektor ocen parametrów strukturalnych ( jako całości ) jest istotnie różny od
zera. Zatem trzy zmienne objaśniające łącznie wywierają istotny wpływ na zmienną
objaśnianą.
6.2 TESTOWANIE POSZCZEGÓLNYCH WSPÓŁCZYNNIKÓW REGRESJI:
Zbadam teraz, czy zmienne objaśniające modelu wpływają w istotny sposób na zmienną
objaśnianą, tzn. czy parametry strukturalne istotnie różnią się od zera.
W tym celu stawiam następujące hipotezę:
H 0 : i =0
wobec hipotezy alternatywnej:
H1 : i 0
Przy testowaniu skorzystam ze statystyki:
tai
ai
gdzie a i - ocena i-tego parametru
Dai
Dai - błąd średni szacunku parametru
Powyższa statystyka ma rozkład t-Studenta o n-k stopniach swobody (n- liczba obserwacji,
k-liczba zmiennych).
Wartość t odczytana z tablic dla 7-3 =4 stopni swobody i przy współczynniku istotności
α=0.05 wynosi:
t =2,132
Jeżeli spełniona jest nierówność t ai > t to hipotezę H 0 odrzucamy na rzecz hipotezy
alternatywnej H1 (czyli dany parametr jest statystycznie istotny). Natomiast w przypadku gdy
t ai t , nie ma podstaw do odrzucenia hipotezy H 0 o nieistotności parametru.
W moim przypadku:
dla stałej:
ta0
=
84.309434
19.434287
= 4.3381799
dla zmiennych objaśniających:
t a1 =
0.031503
0.002566
= 12.277084
12
3.054193E 7
=13.93207
2.192203E 6
21405307
.
=
= 3.4246825
6.250304
t a2 =
ta3
Ponieważ dla wszystkich parametrów spełniona jest zależność t ai > t to hipotezę zerową
H 0 należy odrzucić na korzyść alternatywnej H1 , tak więc wszystkie parametry strukturalne
modelu są statystycznie istotne.
7. ANALIZA WYBRANYCH WŁASNOŚCI SKŁADNIKA LOSOWEGO:
Ważną rolę w procesie weryfikacji modelu odgrywa analiza jego składnika losowego, który
jest zmienną losową o określonym rozkładzie. Badanie własności rozkładu składnika
losowego oraz wybranych parametrów tego rozkładu dostarcza ważnych informacji, będących
podstawą oceny „dobroci” weryfikowanego modelu oraz podejmowania decyzji o
konieczności jego modyfikacji.
Wartości składnika losowego nie są bezpośrednio obserwowalne. Można jednak otrzymać
oceny wartości składnika losowego za pomocą reszt. W związku z tym, wnioski uzyskane z
badania reszt są przenoszone na wnioski o własnościach rozkładu składnika losowego lub
wybranych parametrach tego rozkładu.
Poniżej zamieszczam wyniki dotyczące reszt :
Regression results for AIDS
--------------------------------------------------------------------------------------Observation
Observed
Fitted
Residuals
Standardized
Number
Values
Values
Residuals
1
21.0000
23.8616
-2.86159
-1.89148
2
35.0000
33.6990
1.30096
0.44121
3
50.0000
49.3355
0.66452
0.33847
4
68.0000
67.5026
0.49743
0.17001
5
102.000
98.3722
3.62782
2.20638
6
114.000
116.093
-2.09256
-1.39962
7
136.000
137.137
-1.13658
-1.10154
--------------------------------------------------------------------------------------0 residuals beyond 3 sigma.
Residual Summary
-----------------------------------------------------------------------------Number of observations = 7 (0 missing values excluded)
Residual average = -5.68434E-14
Residual variance = 9.80065
Residual standard error = 3.1306
Coeff. of skewness = 0.350624 standardized value = 0.378717
Coeff. of kurtosis = -0.264967 standardized value = -0.143098
13
Durbin-Watson statistic = 2.08135
7.1 BADANIE LOSOWOŚCI:
Dla modelu z trzema zmiennymi oraz przy siedmiu latach obserwacji zbadanie losowości
reszt za pomocą testu serii jest niemożliwe. W tablicy dla tego testu dla =0.05 przy n 1 =4
oraz k emp =3 gdzie n 1 -liczba reszt dodatnich, k emp -liczba serii, wartość krytyczna k nie jest
podana.
7.2 BADANIE SYMETRII:
Obserwacje odchylające się in minus(in plus) od wartości modelowych powinny stanowić
połowę ( w sensie probabilistycznym) wszystkich obserwacji.
Formułujemy zatem hipotezę, że składnik resztowy ma rozkład symetryczny:
1
H 0 : p
2
wobec hipotezy alternatywnej, że rozkład składnika nie jest symetryczny:
1
H1 : p
2
m
gdzie p , przy czym m jest liczbą reszt odchylających się in plus, a n liczbą wszystkich
n
obserwacji.
Do weryfikacji hipotezy zerowej służy statystyka:
m 1
n 2
t emp =
= 0.353
m m
1
n
n
n 1
W przypadku gdy n 30, powyższa statystyka ma przy założeniu prawdziwości H 0 rozkład
Studenta o n-1 stopniach swobody.
Dla n = 7 i m = 4 oraz α = 0.05 i 7-1= 6 stopniach swobody odczytujemy z tablic wartość
t = 1.943.
Ponieważ t emp =0.353< t =1.943, tak więc nie ma podstaw do odrzucenia hipotezy zerowej o
symetrii składnika losowego.
7.3 BADANIE AUTOKORELACJI:
W celu zbadania czy występuje zjawisko autokorelacji reszt, posłużę się testem von
Neumanna.
14
( nie mogłam użyć w tym celu testu Durbina-Watsona ze względu na brak odpowiednich
wartości krytycznych w tablicach kiedy n =7 i k =3, gdzie n- liczba lat obserwacji, k- liczba
zmiennych w modelu)
Stawiam następujące hipotezy:
H 0 :ξ =0 ( brak autokorelacji)
H 1 : ξ >0
Na podstawie reszt u t oblicza się wartość statystyki Q:
nt 2 ut ut 1
n
Q=
2
n 1t 1 ut 2
n
Obliczoną wartość Q porównujemy z krytyczną wartością Q , taką że zachodzi
P Q Q .
Jeżeli spełniona jest nierówność Q Q to hipotezę H 0 odrzucamy, tzn. występuje
autokorelacja reszt w modelu regresji.
W przeciwnym wypadku ( Q > Q ) nie ma podstaw do odrzucenia hipotezy zerowej.
W moim przypadku dla n =7 i =0.05:
- wartość krytyczna z tablic: Q =1.09
- obliczona wartość: Q =2.42
Ponieważ Q = 2.42> Q =1.09, tak więc nie ma podstaw do odrzucenia hipotezy H 0 o braku
autokorelacji.
7.4 BADANIE ŚREDNIEJ WARTOŚCI :
W celu zbadania średniej wartości reszt posłużę się testem w pakiecie STATGRAPH:
One-Sample Analysis Results
-------------------------------------------------------------------------------WORKAREA.RESIDS
Sample Statistics: Number of Obs.
8
Average
2.27374E-11
Variance
6.70756E6
Std. Deviation
2589.9
Median
-1158.17
Confidence Interval for Mean:
95 Percent
Sample 1
-2165.83 2165.83
7 D.F.
15
Confidence Interval for Variance:
Sample 1
0
Percent
Hypothesis Test for H0: Mean = 0
Computed t statistic = 2.48315E-14
vs Alt: NE
Sig. Level = 1
at Alpha = 0.05 so do not reject H0.
W tabeli umieszczone zostały podstawowe statystyki dla reszt. Obliczona średnia, która
wyniosła 2.48315E-14, jest bardzo bliska zeru. Wobec powyższego nie podstaw do
odrzucenia hipotezy o tym, że średnia reszt równa jest zero.
7.5 BADANIE NORMALNOŚCI ROZKŁADU :
Wykorzystam do tego test pustych cel Davida- Hellwiga.
Stawiam hipotezę H0, że rozkład odchyleń od funkcji trendu jest rozkładem normalnym,
N (0,2.213).
Gdy zostanie spełniona jedna z nierówności:
P(K=k 1 ) < α
P(K=k 2 ) > 1- α, gdzie α - współczynnik istotności
k 1 , k 2 -wartości krytyczne odczytane z tablic
RESZTY
RESZTY
UPORZĄDKOWANE STANDARYZOWANE
NIEMALEJĄCO
ut
-2,86159
-1,29269
-2,09256
-0,94529
-1,13658
-0,51344
0,49743
0,224709
0,66452
0,30019
1,30096
0,587695
3,62782
1,638829
ut
0,0985
0,1711
0,3050
0,5871
0,6179
0,9441
0,9495
CELE
0-0,1429
0,1429-0,2858
0,2858-0,4287
0,4287-0,5716
0,5716-0,7145
0,7145-0,8574
0,8574-1
gdzie ut - wartość dystrybuanty rozkładu normalnego
Odchylenie standardowe reszt = 2.213667
W celu zweryfikowania hipotezy zerowej:
-uporządkowałam reszty rosnąco
-dokonałam standaryzacji reszt według wzoru:
reszta 0
odchylenie. s tan dardowe. reszt
LICZNOŚ
Ć
CEL
*
*
*
**
**
16
-odczytałam z tablic wartości dystrybuanty rozkładu normalnego ut
-podzieliłam odcinek 0,1 na n = 7 równych części tzw. cel
-wyznaczyłam liczbę K=2 cel pustych tj. cel, do których nie trafiła żadna z wartości
odczytanych dystrybuant
-dla n = 7 i = 0,05 odczytałam z tablic wartości krytyczne k1 =0 i k 2 =4
Ponieważ zachodzi nierówność: k1 <K< k 2 ( k1 = 0< K = 2< k 2 = 4), tak więc nie ma podstaw
do odrzucenia hipotezy H 0 o normalności rozkładu reszt.
7.6 BADANIE STAŁOŚCI WARIANCJI W CZASIE:
Do badania stałości wariancji odchyleń losowych w czasie, może być wykorzystany test
istotności współczynnika korelacji t , t między modułami odchyleń losowych a
zmienną czasową t.
W tym przypadku weryfikuje się hipotezę zerową :
H 0 : t 0
przeciwko:
H1 : t 0
Sprawdzianem H 0 jest statystyka :
I
rt n 2
= 0.151
1 rt2
gdzie rt - współczynnik korelacji między modułami reszt a zmienną czasową t
rt
n
t 1
n
t 1
e
t
e
t
e t t
e
t t
2
n
= 0.067
2
t 1
e i t - średnie arytmetyczne et i t.
Z tablic t - studenta odczytuję wartość I * = 2.571 przy =0.05 oraz dla n-2 =7-2 = 5 stopni
swobody.
Jeżeli zachodzi I I * to nie ma podstaw do odrzucenia hipotezy H 0 , tzn. wariancje są stałe
w czasie. W przeciwnym wypadku gdy I I * odrzucamy H 0 na korzyść hipotezy
alternatywnej H1 .
W moim przypadku I 0.0151 I * 2.571 tak więc możemy uznać stałość wariancji w
czasie.
8. PROGNOZA:
Do przeprowadzenia prognozy wykorzystuję dane z roku 1997.
17
Rok
Y
X1
X2
1997 167 50 48
X3
X4
0,0013 3870
Wynik uzyskany za pomocą STATGRAPGA:
Regression results for AIDS10.zachorow
--------------------------------------------------------------------------Observation
Observed
Fitted Lower 95% CL Upper 95% CL
Number
Values
Values for forecasts for forecasts
1
21.0000
23.8616
2
35.0000
33.6990
3
50.0000
49.3355
4
68.0000
67.5026
5
102.000
98.3722
6
114.000
116.093
7
136.000
137.137
8
170.214
152.517
187.911
--------------------------------------------------------------------------Powyższa tabela przedstawia , że dla zadanych wartości zmiennych objaśniających (liczba
zakażonych wirusem HIV homo- i biseksualistów, odsetek zarażonych wirusem HIV drogą
kontaktów heteroseksualnych, liczba leczonych w ośrodkach rehabilitacyjnych dla
narkomanów) prognozowana liczba zachorowań na AIDS w 1997 roku w Polsce wynosi
170.214. Przedział ufności dla prognozowanej wielkości , przy poziomie istotności 0.95-(152.517 , 187.911 ). Rzeczywista liczba zachorowań na AIDS w 1997 roku to 167, tak więc
prognozowana liczba zachorowań nieznacznie różni się od rzeczywistej, bo o 3.214, oraz
mieści się w wyznaczonym przedziale ufności.
Błąd prognozy obliczam w następujący sposób:
I p I p*
Ip
100%
I p - prognozowana liczba zachorowań na AIDS w 1997 roku
I p* - rzeczywista liczba zachorowań na AIDS w 1997 roku
I p = 170.214
I p* = 167
otrzymuję:
170.214 167
100% 19%
.
167
18
9. WNIOSKI:
Model, który otrzymałam nie pokrywa się całkowicie z moimi przypuszczeniami odnośnie
jego wyglądu, które miałam zanim jeszcze przystąpiłam do pracy nad projektem.
Zbudowany przeze mnie model opiera się na trzech zmiennych objaśniających tzn.:
liczba zakażonych wirusem HIV homo- i biseksualistów, odsetek zarażonych wirusem HIV
drogą kontaktów heteroseksualnych oraz liczba leczonych w ośrodkach rehabilitacyjnych dla
narkomanów. Wpływ tych wielkości na liczbę zachorowań na AIDS nie ulega wątpliwości.
Jeżeli wzrośnie ilość zakażeń wśród homo- i biseksualistów a także heteroseksualistów
często zmieniających swych partnerów, wówczas zwiększy się zachorowalność na AIDS.
Również na podstawie zmiennej -leczeni w ośrodkach rehabilitacyjnych narkomanów można
wywnioskować, że skoro leczonych przybywa to z pewnością będzie to miało wpływ na
liczbę chorych na AIDS.
Otrzymany model nie uwzględnia natomiast liczby zakażeń stwierdzonych wśród
narkomanów, który to czynnik wydawał mi się najbardziej obrazujący wpływ na badane
zjawisko, gdyż jest to najliczniejsza z grup badanych.
Żałuję, że nie mogłam wykorzystać danych o dawcach krwi a także o osobach trudniących się
prostytucją i chorych na hemofilię, wtedy bowiem wnioski wypływające z analizy mogłyby
więcej wyjaśnić i zobrazować badany przeze mnie problem.
Ważne jest także zwrócenie uwagi na wielkość próbki. Dane wykorzystane w modelu
obejmowały jedynie 7 lat, była to zbyt mała próbka, co ogranicza stosowalność modelu.
Ponadto w związku z małą liczbą lat obserwacji nie mogłam zweryfikować hipotezy odnośnie
losowości reszt, co jest bardzo istotnym elementem weryfikacji modelu. Również z tego
powodu w celu zbadania zjawiska autokorelacji reszt musiałam posłużyć się testem von
Neumanna, który pod względem ” przydatności ” jest drugi po teście Durbina –Watsona.