Piotr Kowalski

Piotr Kowalski
Grupa nr V
Ćwiczenie nr 8
Zasady kalorymetrii: wyznaczanie pojemności cieplnej
kalorymetru i ciepła właściwego ciał stałych.
1 > Wstęp teoretyczny.
Całą kalorymetrią rządzą trzy główne zasady:
1. Ilość ciepła Q potrzebna do ogrzania ciała o masie m o T [ K ] lub  [ C ] wyraża
się wzorem: Q = cmT lub Q = cm
2. Ilość ciepła oddanego przez ciało jest równa ilości ciepła pobranego przez ciała
otaczające.
3. Ilość ciepła pobrana przez ciało przy podgrzewaniu od temperatury T1 do T2 jest
równa ilości ciepła oddanego przy chłodzeniu w tym samym zakresie temperatur,
jeżeli ciało przechodzi przez te same stany pośrednie w odwrotnym porządku.
nazywamy stosunek ilości ciepła pobranego przez ciało do wywołanego
tym przyrostu temperatury: C = QT. Pojemność cieplna zależy od rodzaju i masy ciała, jego
stanu skupienia, sposobu ogrzewania (pod stałym ciśnieniem lub w stałej objętości)
i temperatury. Jednostką pojemności cieplnej jest [ J/K ].
Pojemnością cieplną
Ciepłem właściwym nazywamy ilość ciepła potrzebną do ogrzania 1 kg dowolnego ciała o 1K.
Jego jednostką jest [ J / kg*K ]
jest to przyrząd do pomiaru ilości ciepła wydzielonego lub pochłoniętego podczas
przemiany fizycznej lub chemicznej. W kalorymetrach nieizotermicznych ilość ciepła określa
się na podstawie zmiany temperatury ciała o znanej pojemności cieplnej, np. określonej
objętości cieczy , w kalorymetrach izotermicznych - na podstawie masy substancji, która
uległa przemianie fazowej (np. topnieniu) w stałej temperaturze.
Kalorymetr
2 > Opracowanie wyników.
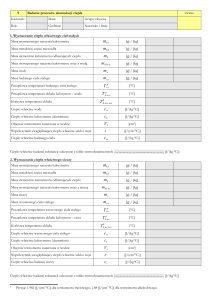
Pojemność cieplna kalorymetru
c – temperatura wody ciepłej = 24.7 [ C ]
z – temperatura wody zimnej = 5.0 [ C ]
m – temperatura wody po wymieszaniu = 16.7 [ C ]
m1 – masa pustego kalorymetru = 258 [ g ]
m2 – masa kalorymetru wraz z wodą ciepłą = 470 [ g ]
m3 – masa kalorymetru z wodą ciepłą i zimną = 681 [ g ]
mc – masa wody ciepłej ( m2 – m1 ) = 212 [ g ]
mz – masa wody zimnej ( m3 – m2 ) = 211 [ g ]
c – ciepło właściwe wody = 4,81 [ kJ / kg * K ] = 4,81 [ J / g * K ]
C – pojemność cieplna kalorymetru
1
   z

C  c m z m
 mc 
 c  m

- wzór na pojemność cieplną
kalorymetru
Aby otrzymać w miarę dokładną temperaturę wody zimnej odczytu dokonałem tuż przed
wlaniem wody do kalorymetru. Temperaturę wody ciepłej oraz „po wymieszaniu”
odczytałem z wykresu interpolacji temperatury ( wykres znajduje się na stronie nr 4 ).
16,70  5,00
J


C  4.81211.00 *
 212,00  464,59
24,70  16,70
K


Ciepło właściwe ciała stałego
c – temperatura ciała tuż przed wprowadzeniem go do kalorymetru = 100 [ C ]
w – temperatura początkowa w kalorymetrze = 11,5 [ C ]
k – temperatura końcowa w kalorymetrze = 15,5 [ C ]
mp – początkowa masa kalorymetru = 258 [ g ]
mk – masa kalorymetru wraz z wodą = 534 [ g ]
mw – masa wody ( mk – mp ) = 276 [ g ]
mc – masa ciała = 219 [ g ]
C – pojemność cieplna kalorymetru = 464,59 [ J / K ]
cw – ciepło właściwe wody = 4,81 [ kJ / kg * K ] = 4,81 [ J / g * K ]
cc – ciepło właściwe badanego ciała
cc 
c w mw  C  k   w
mc
c  k
- wzór na ciepło właściwe
ciała stałego
Podobnie jak w poprzednim przypadku aby uzyskać temperatury w i k skorzystałem z
wykresu interpolacji temperatury ( wykres 2, strona 5 ).
cc 
4,81 * 276  464,59 15,5  11,5
J
J
 0,38737
 387,37
219
100  15,5
g*K
kg * K
3 > Rachunek błędów.
Aby obliczyć błąd pojemności cieplnej { C } kalorymetru, oraz błąd ciepła właściwego {
cc } ciała stosuję wzór na tzw. przeniesienie niepewności:
2
2
2
2
  c   m z     m     z    c    mc 
 
 
    
 

C
 c   m z    m    z    c   mc 
C
 cc
cc
2
2
2
2
  c    m    C   mc    k
  
  w    w   
  
 c w   m w   C   mc    k
2
2
2
2
2
    w    c 
  
  

  w   c 
2
Gdzie:
 C – szukany błąd pojemności cieplnej kalorymetru.
 c – błąd ciepła właściwego wody ( ponieważ wartość ciepła właściwego wziąłem z
„Tablic matematyczno – fizycznych” za błąd przyjmuję 0 ).
 mz , mc– błąd masy wody zimnej/ciepłej. Przyjmuję dokładność wagi, czyli 1 [ g ].
 m , c , z – błąd temperatury wody wymieszanej/ciepłej/zimnej. Przyjmuję
dokładność termopary, czyli 0.1 [oC].
 cc – szukany błąd ciepła właściwego ciała stałego.
 cw – błąd ciepła właściwego wody ( ponieważ wartość ciepła właściwego wziąłem z
„Tablic matematyczno – fizycznych” za błąd przyjmuję 0 ).
 mw , mc– błąd masy wody/ciała stałego. Przyjmuję dokładność wagi, czyli 1 [ g ].
 C – błąd pojemności cieplnej kalorymetru obliczony powyżej.
 k , w , c – błąd temperatury początkowej/końcowej wody/ciała stałego.
Przyjmuję dokładność termopary, czyli 0.1 [oC].
2
2
2
2
2
2
 0   1   0,1   0,1   0,1   1 
 
 
 
 
 
 * 464,59  10,36
 4,81   211   16,7   5,0   24,7   212 
 C 
2
2
2
2
2
2
2
 0   1   10,36   1   0,1   0,1   0,1 
 cc  
 
 
 
 
 
 
 * 387,37  9,87
 4,81   276   464,59   219   15,5   11,5   100 
4 > Podsumowanie wyników
Otrzymane przeze mnie wyniki to :
 Pojemność cieplna kalorymetru
C  464,59  10,36 J K
 Ciepło właściwe badanego ciała
cc  387,37  9,87 J kg * K
3