Elementy i Obwody Elektryczne

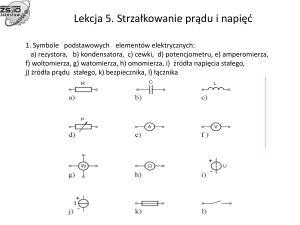
Elementy i Obwody Elektryczne
Element ( element obwodowy) – jedno z podstawowych pojęć teorii obwodów.
Element jest modelem pewnego zjawiska lub cechy fizycznej związanej z
obwodem. Elementy (jako modele) mogą mieć róŜny stopień komplikacji.
Funkcja zaciskowa
(obwodowa)
Funkcja zaciskowa
(obwodowa)
ELEMENT
u(t)
Zacisk
A
i(t)
Zacisk
B
Końcówka
Końcówka
Element dwuzaciskowy (dwukońcówkowy) – DWÓJNIK
Strzałkowanie odbiornikowe !
Funkcje zaciskowe elementu: prąd elementu i(t) oraz napięcie elementu u(t)
związane są ze sobą równaniem elementu, które definiuje dany element i określa
jego podstawowe właściwości.
W TO UŜywane są elementy wielozaciskowe: trójnik, czwórnik itd.
Obwody, układy, sieci
Obwód – moŜliwie najprostsze połączenie elementów umoŜliwiające
przepływ prądu elektrycznego.
Układ ( obwód rozgałęziony ) – struktura bardziej rozbudowana niŜ obwód.
Sieć – bardzo duŜy układ.
Podstawowe modele zjawisk w obwodzie
Zjawisko:
Element:
BEZSTRATNY PRZEPŁYW PRĄDU
ZWARCIE ( GALWANICZNE )
i
u≡0
Równanie elementu:
∀u ≡ 0
i
Moc chwilowa z jaką zwarcie pobiera energię elektryczną z obwodu:
p(t) = u(t) i(t) = 0⋅⋅i (t) ≡ 0
Zjawisko:
Element:
BRAK PRZEPŁYWU PRĄDU
ROZWARCIE ( PRZERWA)
i≡0
u
Równanie elementu:
∀i ≡ 0
u
Moc chwilowa z jaką rozwarcie pobiera energię elektryczną z obwodu:
p(t) = u(t) i(t) = u (t)⋅⋅0 ≡ 0
Zjawisko:
ROZPRASZANIE ( DYSSYPACJA )
ENERGII ELEKTRYCZNEJ
OPÓR LINIOWY
Element:
i
R (G)
u
Równanie elementu ( POSTULAT OHMA ):
u = R⋅⋅i
Jednostki:
R:
G:
lub
G = R–1
i = G⋅⋅u
Strzałkowanie odbiornikowe !
[Ω
Ω] – ohm
[S] – simens
Opór jest elementem dyssypatywnym (rozpraszającym) bezinercyjnym.
U
l
R = =ρ
I
S
U
ρ
S
I
l
 Ω ⋅ mm2 
ρ
 – opór właściwy materiału
 m 
Moc chwilowa z jaką opór przetwarza energię elektryczną:
pR(t) = u(t) i(t) = R i 2(t) = G u2(t) ≥ 0
Przykład. Jaka jest rezystancja przewodu miedzianego o przekroju S= 2,5 mm2 i długości
l= 50 m.
ODP
ρ Cu = 0,0175
[
Ω⋅ mm 2
m
] = 0,0175 [µΩ ⋅ m] – rezystancja właściwa miedzi
R = 0,0175
50
= 0,35 Ω
2,5
Uwaga: średnica przewodu wynosi: D= 0,89 mm (dosyć cienki!)
Przykład. Z jaką mocą wydziela się energia elektryczna z przewodu z poprzedniego
zadania przy przepływie prądu i= 2 A.
p(t ) = R ⋅ i 2 = 1,4 W
ODP
Przykład Do jakiej temperatury T nagrzeje się przewód z poprzednich zadań podczas
godzinnej pracy. Temperatura początkowa T0= 293 K. ZałoŜenie: brak chłodzenia!
ODP
Wydzielona energia elektryczna:
W = p ⋅ t = 5,04 kJ
W = k ⋅ Q = k ⋅cCu ⋅m ⋅ ∆T = k ⋅cCu ⋅γ Cu ⋅ V ⋅ ∆T
 kcal 
c Cu = 0,092 
 = 0,092
kg
⋅
K


 kg 
γ Cu = 8,9  3  = 8900
 dm 
 cal 
 g ⋅ K  – ciepło właściwe miedzi


 kg 
6  g 
=
8
,
9
⋅
10
 m 3 
 m 3  –
gęstość miedzi
 J 
k = 4,1868   – przelicznik kalorii na dŜule
 cal 
Objętość przewodu:
V = S ⋅ l = 2,5 ⋅ 10−6 ⋅ 50 = 125 ⋅ 10−6 m 3 = 0,125 dm 3
Masa przewodu:
m = γ Cu ⋅V = 8,9 ⋅ 0,125 = 1,1125 kg
Przetworzona energia:
W = kQ = 4,1868 ⋅ 0,092 ⋅ 1,1125 ⋅ 103 ⋅ ∆T = 428,519 ⋅ ∆T
Przyrost temperatury:
∆T = T − T0 =
5040
= 11,76 K
428,519
Temperatura przewodu:
T = T0 + ∆T = 293 + 11,76 = 304,76 K
R=5Ω (G=
Dane:
Przykład
T = 31,76 oC
1 1
=
5  Ω 
0,2 S )
u(t) = 10⋅1(t) – 15⋅1(t–2) + 5⋅1(t–3) [V]
Obliczenia: i(t) = u(t) ⋅G = 2⋅1(t) – 3⋅1(t–2) + 1⋅1(t–3) [A]
i(t) [A]
u(t) [V]
+1
t [s]
2
–5
t [s]
+2
–1
3
2
3
p(t) = G⋅u (t) = R⋅i (t)
2
2
u2(t) = 100⋅1(t) – 75⋅1(t–2) – 25⋅1(t–3)
i2(t) [A2]
u2(t) [V2]
+4
+100
+2
+1
t [s]
2
t [s]
2
3
3
p(t)=G⋅u2(t) = 20⋅1(t) – 15⋅1(t–2) – 5⋅1(t–3)
wR(0,t) [J]
p(t) [W]
45
40
+20
20
+5
t [s]
t [s]
2
3
1
2
3
Zjawisko:
Element:
GROMADZENIE ( KONSERWACJA )
ENERGII ELEKTRYCZNEJ
POJEMNOŚĆ LINIOWA
C
q
i
u
Równania elementu :
q = C⋅⋅u
dq
du
i=
=C
dt
dt
Jednostki:
C:
q:
Strzałkowanie odbiornikowe !
[F]
– farad = 1A⋅1s⋅1V–1
[C]
– kulomb = 1A⋅1s
d u( t )
i( t ) = C
dt
t
1
u( t ) = ∫ i( τ )dτ + u(t0 )
C t0
Pojemność jest elementem konserwatywnym inercyjnym.
Moc chwilowa z jaką energia elektryczna jest gromadzona w polu
elektrycznym pojemności:
dq(t )
[W]
pC ( t ) = u ( t ) ⋅ i ( t ) = u ( t ) ⋅
dt
q
S
C= =ε
u
d
–q
ε=εw⋅ε0
S
ε = ε wε 0 – przenikalność elektryczna
+q
ε0 =
d
1
F
⋅ 10 −9   –
36π
m
przenikalność elektryczna próŜni
Przykład Jaka jest przybliŜona pojemność kondensatora powietrznego o
kołowych okładkach mających średnicę D= 30 cm i oddalonych o d= 0,3 mm.
ODP εw≅ 1 – bo, powietrze ;
Powierzchnia okładek:
S=
1
9
π = 0,071 m 2
πD 2 =
4
400
1
S 10−9 9π 10+4
⋅
⋅
=
⋅ 10−7 F = 2,1 nF
Cp = ε 0 =
d 4π ⋅ 9 400 3
48
Przykład Jaka jest przybliŜona pojemność kondensatora z poprzedniego
przykładu jeśli zostanie on wypełniony polistyrenem?
ODP εw≅ 2,65 – przenikalność względna polistyrenu;
S
C1 = ε wε 0 = ε w ⋅ Cp = 2,65 ⋅ 2,1 nF = 5,56 nF
d
Przykład Jaki ładunek zostanie zgromadzony na okładkach kondensatora z
poprzedniego przykładu jeśli podłączymy je do źródła o napięciu 200 V?
ODP
Q = CU = 5,56 ⋅ 10 −9 ⋅ 200 = 1,113 µC
Przykład Ile energii zostanie zgromadzonej w kondensatorze z poprzedniego
przykładu?
ODP
QU CU2 Q2
W=
=
=
2
2
2C
W= 111,2 µJ
Zjawisko:
GROMADZENIE ( KONSERWACJA )
ENERGII ELEKTRYCZNEJ
INDUKCYJNOŚĆ LINIOWA
Element:
L
i
ψ
u
Równania elementu :
ψ = L⋅⋅i
dψ
di
u=
=L
dt
dt
Jednostki:
L:
ψ:
Strzałkowanie odbiornikowe !
[H]
– henr = 1V⋅1s⋅1A–1
[Wb]
– weber = 1V⋅1s
d i( t )
u( t ) = L
dt
t
1
i( t ) = ∫ u( τ )dτ + i(t0 )
L t0
Indukcyjność jest elementem konserwatywnym inercyjnym.
Moc chwilowa z jaką energia elektryczna jest gromadzona w polu
magnetycznym indukcyjności:
dψ ( t )
pL ( t ) = u( t ) ⋅ i( t ) =
⋅ i( t ) [ W ]
dt
Zjawisko:
DOSTARCZANIE LUB POBIERANIE
ENERGII ELEKTRYCZNEJ
ŹRÓDŁO NAPIĘCIA ( DOWOLNA MOC CHWILOWA )
Element:
e
ie
u
Równania elementu :
e – dowolne ( zadane )
ie – wymuszone przez
obwód zewnętrzny
Strzałkowanie źródłowe !
e [V]
pe > 0
pe < 0
E
Pp
e
i
i [A]
i
Charakterystyka źródła napięcia o
stałej wartości: e(t) = E = const
!?
Moc chwilowa energii elektrycznej źródła napięcia:
pe ( t ) = u( t ) ⋅ i( t ) = e( t ) ⋅ ie ( t ) [W ]
pe(t) > 0 – źródło oddaje energię
pe(t) < 0 – źródło pobiera energię
Zjawisko:
Element:
DOSTARCZANIE LUB POBIERANIE
ENERGII ELEKTRYCZNEJ
ŹRÓDŁO PRĄDU ( DOWOLNA MOC CHWILOWA )
j
i
uj
Równania elementu :
j – dowolne ( zadane )
uj – wymuszone przez
obwód zewnętrzny
Strzałkowanie źródłowe !
j [A]
pj < 0
pj > 0
J
j
Pp
i
u [V]
up
Charakterystyka źródła prądu o stałej
wydajności: j(t) = J = const
!?
Moc chwilowa energii elektrycznej źródła prądu:
p j ( t ) = u( t ) ⋅ i( t ) = uj ( t ) ⋅ j ( t ) [W ]
pj(t) > 0 – źródło oddaje energię
pj(t) < 0 – źródło pobiera energię
Element:
ŹRÓDŁO STEROWANE
i1≡0
i2
i2
k⋅u1
r⋅i1
u1
u2
u2
ZNSP ( CCVS )
ZNSN ( VCVS )
i1≡0
i1
u1≡0
i2
i2
α i1
g u1
u1
ZPSN ( VCCS )
u2
u1≡0
i1
u2
ZPSP ( CCCS )
W przypadku źródeł sterowanych moc chwilowa „pierwotna” jest
zawsze równa zero: p1(t) ≡ 0 co oznacza, Ŝe źródła nie pobierają
energii od strony sterowania.
Postulaty Teorii Obwodów
Prądowy Postulat Kirchhoffa ( PPK )
∑i = 0
Algebraiczna suma prądów we węźle jest równa zero.
Napięciowy Postulat Kirchhoffa ( NPK )
∑u = 0
Algebraiczna suma napięć w oczku jest równa zero.
Postulat Ohma ( PO )
u = R ⋅ i lub
i = G ⋅u
1 1
G [S] =  
R Ω
Zjawisko:
DOSTARCZANIE LUB POBIERANIE
ENERGII ELEKTRYCZNEJ
NAPIĘCIOWE ŹRÓDŁO ENERGII
(OGRANICZONA MOC CHWILOWA)
Element:
U
E
I
r⋅I
r
Równania elementu :
E – dowolne ( zadane )
I – wymuszone
Strzałkowanie źródłowe !
NPK:
(+U) + (– E) + (+ r I) = 0
p = U⋅I = E⋅I – r⋅I2
U= E–rI
p [W]
U [V]
p<0
U0= E
Up
p>0
p max =
Pp(0,5Iz,0,5E)
→ pmax
rIp
Iz =
E
r
I [A]
Iz =
E2
4r
E
r
I [A]
Ip =
E 1
= 2 Iz
2r
p<0
p<0
p>0
Ip
p<0
Zadanie 1 Przedyskutować prądowe źródło energii i porównać jego
zachowanie w róŜnych stanach pracy ze źródłem prądu.
Łączenie elementów bezźródłowych dwuzaciskowych
Połączenie szeregowe ( dzielnik napięcia )
u1
A i1
u2
i2
D1
B
……
D2
i = i1 = i2 = …
u = u1 + u2 + …
u
A
i
B
Dz
Rezystory
Rz = R1 + R2 + L = ∑ Rk
Rz > max Rk
Indukcyjności
Lz = L1 + L2 + L = ∑ Lk
Lz > max Lk
( bez sprzęŜeń )
Lz = L1 + L2 + 2 ⋅ ( ± M )
Indukcyjności
(ze sprzęŜeniem)
1
1
1
1
=
+
+ L= ∑
Cz C1 C2
Ck
Pojemności
k
k
(+M) sprz. Zgodne
(–M) sprz. Przeciwne
Cz < min Ck
k
Rezystancyjny Dzielnik Napięcia (nie obciąŜony)
uk
i
u1
u2
R1
R2
uN
i1 ≡ 0
Rk
u
uk =
Rk
N
∑R
i =1
i
 Rk 
⋅u =   ⋅u
 Rz 
RN
Przykład Jakie będzie napięcie U2 na rezystorze R2 jeśli nieobciąŜony dzielnik napięcia
zasilany jest napięciem U= 24 V. Dane: R1= 24 Ω, R2= 47 Ω, R3= 12 Ω.
U2
R1
R2
R3
U2 =
R2
47
U=
24 = 13,59 V
R1 + R2 + R3
24 + 47 + 12
U
Przykład „Tradycyjne” Ŝaróweczki stosowane do oświetlenia choinki mają moc P= 5 W
przy napięciu U= 14 V. Ile takich Ŝaróweczek naleŜy połączyć szeregowo, jeśli napięcie
sieci zasilającej wynosi Uz= 230 V. Jaka jest moc elektryczna takiego „łańcucha świateł”?
Rezystancja Ŝaróweczki:
U 2 14 2
R=
=
= 39,2 Ω
P
5
Rezystancja łańcucha:
R0 = N ⋅ R = 17 ⋅ 39,2 = 666,4 Ω
U
N = z = 16,43 ;
U
Moc łańcucha:
N= 17
U z2
P0 =
= 79,38 W
R0
Przykład Połączono szeregowo Ŝaróweczkę o parametrach znamionowych U1= 12 V,
P1= 5 W z Ŝarówką o parametrach znamionowych P2= 100 W, U2= 230 V i włączono na
napięcie U= 230 V. Co się stanie?
P2, U2
P1, U1
R1
U
U 22
R2 =
= 529 Ω
P2
R1
U = 11,87 V – świeci pełnym światłem
R1 + R2
R2
U 21 =
U = 218,3 V – świeci trochę słabiej
R1 + R2
U
I0 =
= 0,41 A
P0 = U ⋅ I 0 = 94,84 W
R1 + R2
U 11 =
U
R2
U12
R1 =
= 28,8 Ω
P1
Połączenie równoległe ( dzielnik prądu )
u1
u
i1
D1
A i
B
A
i
Dz
u1
i2
B
D2
ik
……
uN
iN
u = u1 = u2 = …
i = i1 + i2 + …
u=u +u +…
DN
Rezystory
Indukcyjności
( bez sprzęŜeń )
Indukcyjności
(ze sprzęŜeniem)
Kondensatory
G z = G1 + G2 + K = ∑ Gk
Gz > max Gk
1
1 1
1
= + + L= ∑
Lz L1 L2
Lk
Lz < min Lk
k
k
L1 L2 − M 2
Lz =
L1 + L2 − 2 ⋅ ( ± M )
(–M) sprz. Przeciwne
Cz = C1 + C2 + L = ∑ Ck
Cz > max Ck
(+M) sprz. Zgodne
k
Konduktancyjny Dzielnik Prądu ( nie obciąŜony )
u
i1
i
i2
ik
G1
G2
Gk
ik =
Gk
N
∑G
i =1
iN
GN
i
 Gk 
⋅i =   ⋅i
 Gz 
Wybrane Zasady i Twierdzenia Teorii Obwodów
Przekształcenie „gwiazda ↔ trójkąt”
C
B
GBC
C
B
RB
RC
GCA
RA
GBA
A
A
R AB RCA
RAB + RBC + RCA
R AB RBC
RB =
RAB + RBC + RCA
RBC RCA
RC =
RAB + RBC + RCA
RA =
G A GB
G A + GB + GC
GB GC
=
G A + GB + GC
GC G A
=
G A + GB + GC
G AB =
GBC
GCA
Przykład Przeliczyć wartości rezystorów symetrycznego czwórnika kształtu T na
wartości rezystorów symetrycznego czwórnika kształtu Π.
2
1
25,97 Ω
25,97 Ω
G0 = G A + GB + GC =
+
= 0,1055 S
25,97 35,14
35,14 Ω
R2
R1
R3
1
1
⋅
25,97 35,14
G1 =
= 0,01039 S
0,1055
1
1
⋅
25,97 25,97
G2 =
= 0,01406 S
0,1055
1
1
⋅
25,97 35,14
G3 =
= 0,01039 S
0,1055
 R1 = 96,25 Ω

 R2 = 71,13 Ω
 R = 96,25 Ω
 3
RównowaŜność zaciskowa źródeł energii
i
i
A
A
R
u
OBC.
G
j
OBC.
u
e
B
NZE
PZE
B
i=j–Gu
u=e–Ri
Warunki równowaŜności zaciskowej
R⋅⋅ G = 1
e = R⋅⋅ j ∨ j = G⋅⋅ e
Przykład 1
i
i A
A
2Ω
0,5 S
5A
u
u
10 V
B
B
0
NZE:
U = 10 V, Iz = 5 A;
u = 10 – 2 i
PZE:
0
U = 10 V, Iz = 5 A;
i = 5 – 0,5 u
Przykład 2
i
A
i
6Ω
u
i
A
4Ω
30 V
40 V
B
w
u
u
w
A
2Ω
5A
1
S
4
10 A
i
A
5A
1
S
6
u
10 V
B
B
1
S
2
B