pobierz plik

sprawdziany:
2-06-2006
Tory teletransmisyjne
Tory teletransmisyjne miedziane
1. Para skręcana (skrętka) – stosowana do budowy sieci lokalnych
do 10Mbit/s dla długości 100m.
2. Kabel koncentryczny
Impedancja falowa typowe wartości 50Ω lub 75Ω
Stosowana teoria linii długiej. Linia powoduje zmianę amplitudy
i fazy sygnału w zależności od częstotliwości, co powoduje
zniekształcenie sygnału.
Przykładowo na wyjściu sygnał będący sumą sygnału o
częstotliwości 1kHz i 3kHz
wejście
wyjście
sygnał wejściowy
sygnał
wejściowy
sygnał
wyjściowy
Odcinek linii o długości δx modelujemy:
i(x+δx,t)
i(x,t)
u(x,t)
u(x+δx,t)
R,G,L,C – stałe kilometryczne linii
Równania opisujące prąd i(x,t)
i spadek napięcia wzdłuż linii u(x,t):
u
i

 Ri  L
x
t
i
u

 Gu  C
x
t
Typowe wartości stałych kilometrycznych to: R≈100Ω/km,
G≈10μS/km, L≈0.25mH/km, C≈0.1μF/km
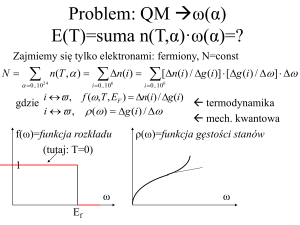
Przyjmiemy sygnał sinusoidalnie zmienny o pulsacji ω
i zastosujemy metodę amplitud zespolonych czyli
i(x,t)=Re[I(x)ejωt], u(x,t)=Re[U(x)ejωt]
gdzie I(x), U(x) - amplitudy zespolone odpowiednio prądu i napięcia.
Ze względu na liniowość układu równań telegrafistów mamy:
dU

 R  jL I
dx
dI

 G  jCU
dx
Eliminując prąd otrzymujemy:
bądź eliminując napięcie:
gdzie

d2U
2


U0
2
dx
d 2I
2


I0
2
dx
R  jL G  jC
- stała propagacji
Stałą propagacji można zapisać w postaci: γ=α+jβ
α – jest liczbą rzeczywistą i jest nazywane tłumiennością
jednostkową toru. Podawane jest w neperach.
β – jest liczbą rzeczywistą i jest nazywane przesuwnością.
Rozwiązując równanie:
  j   RG1  jT1 1  jT2 
2
Mamy:

  0.5RG 1  2T1T2  1  2 T12  T22  T1T2 

2
T1  T2  0.5RG

1  2T1T2  1  2 T12  T22  T1T2 
gdzie
L
T1 
i
R
2

C
T2 
G
d2U
2
Rozwiązanie równania:


U0
2
dx
ma postać:
Ux   A1e x  A 2e x

2
dI
2


I0
2
dx
i podobnie dla amplitudy zespolonej prądu mamy:
Ix   B1e x  B 2e x
Ze względu na równanie:
dU

 R  jL I
dx
znajdujemy związek między stałymi A1, A2 i B1, B2:
 A1 e x  A 2 e x  R  jL B1e x  B 2e x 
i mamy:

1
B1  
A1   A1
R  jL
zc

1
B2 
A2  A2
R  jL
Zc
gdzie
R  jL
- impedancja falowa
zc 
G  jC
Rozwiązania dla amplitud zespolonych napięcia i prądu są:
Ux   A1e x  A 2e x
A 1 x A 2  x
I x    e 
e
zc
zc
Niech stałe A1 i A2 są liczbami zespolonymi o postaci:
A1=|A1|ejφ
i A2=|A2|ejθ
biorąc pod uwagę, że γ=α+jβ możemy zapisać:
Ux   A1 ex jx    A 2 e  x j x  
mnożąc zespoloną amplitudę napięcia przez ejωt i biorąc część
rzeczywistą mamy rzeczywisty rozkład napięcia u(x,t) w linii:
ux, t   ReUx e jt   Re A1 ex jx  t   A 2 e  x j x  t  
Biorąc część rzeczywistą mamy:
ux, t   A1 ex cos t   x     A 2 e  x cos t   x   
Oznaczmy up(x,t)=cos(ωt-βx+θ)
i uo(x,t)=cos(ωt+βx+θ)
Niech Φ=ωt0–βx0 +θ – faza funkcji cosinus w chwili t0 w punkcie
x0 i zobaczmy co dzieje się dla kolejnych chwil t>t0
cos(ωt-βx+φ)
Obraz stałej fazy: ωt-βx+φ=const porusza się z prędkością
dx 
vf 

dt 
prędkość ta jest nazywana prędkością fazową.
Biorąc pod uwagę:

T1  T2  0.5RG

1   T

  T T  
1   T1T2  1   T  T  T1T2 
2
2
2
1
2
2
2
2
2
2
1


T
T


T
1 2
1
2
mamy: v 
f
T1  T2  0.5RG
2
2
1
2
zależność prędkości fazowej od pulsacji (częstotliwości)
nazywamy dyspersją.
Ponieważ fala up(x,t)=cos(ωt-βx+θ) porusza się w kierunku
dodatnich x będziemy ją nazywać falą padającą.
Niech Θ=ωt0+βx0+θ i zbadamy jak propaguje się stała faza
dla funkcji uo(x,t)=cos(ωt+βx+θ) dla czasów t>t0
cos(ωt+βx+θ)
Fala porusza się w kierunku malejących x i będziemy ją
nazywali falą odbitą.
Obraz stałej fazy: ωt+βx+θ=const porusza się z prędkością
dx

vf    
dt

a więc co do wartości bezwzględnej prędkość fazowa fali odbitej
ma tę samą wartość co prędkość fali padającej.
Rozpatrzmy wpływ tłumienności α na rozkład fali wzdłuż linii.
Tłumienność α:
  0.5RG 1   T1T2 
2
1   T
2
2
1
2


 T  T1T2 
2
2
powoduje, że następuje tłumienie amplitudy fali wzdłuż linii:
1
-αx)
u
|A2(|ex
-|A
|e-αx
 2u
( x)
0.5
0
xcos(ωt-βx+φ)
)
|Ai2|e(-αx
0.5
1
0
0.5
1
x
1.5
2
Rozważmy na wejściu linii transmisyjnej sygnał zmodulowany
amplitudowo: swej(t)=[1+mcos(ωt)]cos(ωct)
2
(swejx(t))
1+m(t)
1
m ( x)
 (-[1+m(t)]
1m ( x) )
0
2
0
0.5
1
t
x
1.5
2
Na wyjściu mamy sygnał swyj(t):
0.5
sw(t)( x)
swyj
1e  m ( x) 
1 
2
-[1+m(t)]
 e  1e  m ( x) 
1
1+m(t)
e 
0.25
2
0
0.25
0.5
0
0.5
1
x
1.5
2
Idealną byłaby sytuacja gdyby tłumienność α=0. Możemy to
uzyskać, jeżeli

  0.5RG 1   T1T2  1   T  T  T1T2 
2
2
2
1
2
2
2

R≈0 i G≈0
Linia spełniająca powyższe warunki nazywa się linią bezstratną
Dla linii bestratnej mamy:
  j LC
L
zc 
a więc α=0 i    LC
impedancja falowa
C
jest liczbą rzeczywistą, a prędkość fazowa: v  1
f
LC
nie zależy od częstotliwości, co oznacza, że nie występuje
dyspersja.
Przykładowo linią bezstratną jest linia anteny telewizyjnej
w pasmie kanałów 21 – 35, które znajdują się w zakresie
od 470 – 590 MHz.
Typowe parametr kabla antenowego: C=0.1 μF/km, R=100 Ω/km,
G=10 μS/km i L=0.25 mH/km mamy dla 500 MHz:
ωC=314 S/km>>G=10 μS/km
oraz
ωL=0.785 MΩ/km>>R=100 Ω/km
Praktycznie można pominąć wpływ rezystancji i upływności
na przesył sygnału, jeżeli ωL > 10R oraz ωC > 10G
W zakresie niskich częstotliwości wpływ rezystancji i upływności
nie może być zaniedbany i wtedy naszym celem jest tak dobrać
parametry linii aby sygnał nie uległ odkształceniu.
Oznacza to, że tłumienność α i przesuwność β:
ux, t   A1 ex cos t   x     A 2 e  x cos t   x   
powinny: α – musi być niezależne od częstotliwości (pulsacji),
β – musi być liniową funkcją częstotliwości.
Dla uzyskania tego:

  0.5RG 1   T1T2  1   T  T  T1T2 
2

2
2
1
2
2
2
T1  T2  0.5RG

1   T1T2  1   T  T  T1T2 
2
L
T1 
i
R
2
C
T2 
G
można to uzyskać, jeżeli
2
1
2
2
2

L
C
T1   T2   T
R
G

bo wtedy mamy:



1   T  T  T1T2   1   2T  T
2
2
1
2
2
2
2

2
 1  2T   T   1  T 
2
i 
4
 
2 2

2 2

2
2
1
2
2
2
 0.5RG 1  T   1  T   RG
2


0.5RG 1   T1T2  1   T  T  T1T2  
2
2
T1  T2  0.5RG

1  2T1T2  1  2 T12  T22  T1T2 
2T 0.5RG

 T RG
2
2


a więc tłumienność linii:   2RG jest niezależna od
częstotliwości i przesuwność:   T 2RG jest liniową
funkcją częstotliwości.
Jeżeli linia jest nieodkształcająca, co oznacza, że
L C

R G
R  jL
to również jej impedancja falowa: z c 
G  jC
jest niezależna od częstotliwości i równa:
R
zc 
G
a rozwiązanie ma postać:
ux, t   A1 e
RG x
 A 2 e
cost  T RGx    
RG x
cost  T RGx   
1
Prędkość fazowa fali: v f 
LC
jest identyczna jak dla linii bezstratnej i nie zależy od
częstotliwości, a więc nie następuje zniekształcenie sygnału
wywołane dyspersją.
L C
Warunek:
jest niespełniony w typowych kablach

R G
Dla linii o typowych parametrach: C=0.1 μF/km, R=100 Ω/km,
G=10 μS/km i L=0.25 mH/km mamy:
L
C
 2.5 s   10 ms
R
G
Jedynym możliwym rozwiązaniem jest zwiększenie stałych
kilometrycznych linii.
W grę wchodzą dwa parametry G – upływność linii. Jednak
zwiększenie tego parametru prowadzi do wzrostu   RG
i w efekcie prowadzi do wzrostu tłumienia sygnału, co jest
niewskazane.
Dlatego stosuje się zwiększanie drugiego parametru
L – indukcyjności linii. W praktyce wykonuje się to w ten sposób,
że w ustalonych odstępach wprowadza się do linii cewki, które
dobiera się w ten sposób aby uzyskać spełnienie warunku dla
danego odcinka linii o długości d:
Ld  Lp C

Rd
G
skąd wartość indukcyjności cewki:
C

L p   R  L d
G

i dla linii o parametrach: C=0.1 μF/km, R=100 Ω/km, G=10 μS/km
i L=0.25 mH/km mamy: 1 H, co kilometr lub 0.5 H co pół kilometra
Czynność powiększania indukcyjności linii przez wprowadzenie
dodatkowych indukcjności skupionych nazywa się pupinizacją.
Niestety wprowadzenie skupionej indukcyjności powoduje,
że uzyskuje się linię nieodkształcającą w wąskim pasmie
niskich częstotliwości. Aby operacja była skuteczna w szerokim
pasmie należałoby wprowadzić indukcyjność równomiernie
rozłożoną, taką próbą jest tzw. krarupizacja.
Krarupizacja polega na owinięciu żyły przewodzącej dodatkowym
przewodem wykonanym z materiału o bardzo wysokiej względnej
przenikalności magnetycznej, co powoduje wzrost indukcyjności.
Niestety również ten zabieg daje efekty tylko w zakresie kilku kHz.
Pupinizacja powoduje spowolnienie sygnału, gdyż prędkość:
1
vf 
L  Lp C
i dla C=0.1 μF/km, R=100 Ω/km, G=10 μS/km, L=0.25 mH/km
i Lp=1 H/km mamy: 3160 km/s, a więc w czasie 0.5 s sygnał
przebywa drogę: 1580km czyli biorąc pod uwagę rozmowę
telefoniczną w odległości 790 km słyszymy odpowiedź po 0.5 s,
co jest niedopuszczalne przy transmisji sygnałów telefonicznych.
Pupinizacja powoduje ograniczenie pasma częstotliwości
przesyłanych sygnałów analogowych. Nie jest stosowana dla
sygnałów cyfrowych.
Prędkość fazowa i prędkość grupowa
Prędkość fazową dla dowolnej linii definiujemy:

vf 

i dla linii opisanej przez stałe kilometryczne R, L, G, C jest:

1   T1T2  1   T  T  T1T2 
vf 
T1  T2  0.5RG
2
gdzie T1 
L
i
R
2
2
1
2
2
2

C
T2 
G
Natomiast prędkość grupowa:

vg 

opisuje zmianę nachylenia obwiedni fali sinusoidalnej i zależność
prędkości grupowej od częstotliwości powoduje zmianę kształtu
obwiedni, a tym samym zniekształcenie przesyłanej informacji.
Odbicia
Sygnał propagujący się w torze transmisyjnym bez strat:
ux, t   A1 cost  x     A2 cost  x  
możemy ogólnie rozłożyć na dwie fale:
falę padającą zależną od argumentu ωt-βx
i opisującą falę wędrującą w kierunku rosnących x,
i falę odbitą zależną od argumentu ωt+βx
opisującą falę wędrującą w kierunku malejących x.
Zapiszemy krótko:
ux, t   up x  vt   uo x  vt   up  uo
Dla prądów mamy podobną sytuację, czyli:
ix, t   i p x  vt   i o x  vt   i p  i o
Z równań dla linii bez strat mamy:
u
i

L
x
t
i
u

C
x
t
i podstawiając znajdujemy:
du p   du o   
u 

 u p x  vt   u o x  vt  

x x
x
d x
d x

  x  vt i
1
gdzie
x

  x  vt i
1
x
u du p du o


a więc ostatecznie:
x d d
Dla prądu mamy:
di p   di o   
i 

 i p x  vt   i o x  vt  

t t
t
d t
d t

 v
ale   x  vt i
x

  x  vt i
v
x
di p

i
di o
i podstawiając mamy:
 v
v
t
d
d
u
i
Podstawiając do równania: 
L
x
t
mamy:
du p du o
di p
di o


  vL
 vL
d d
d
d
Pamiętając, że dla linii bezstratnej vL=zc i porównując
funkcje o tych samych argumentach mamy:
up  z ci p
uo  z ci o
up, ip
uo, i0
uk, ik
zodb
Dla obciążenia na końcu
linii mamy bilans:
uk  up  uo
ik  ip  io
u k  i k z odb

Eliminując napięcie uk i prąd ik mamy: u p  u o  z odb i p  i o
a korzystając z równań:
up  z ci p
uo  z ci o
mamy:
z odb  z c
uo 
up
z odb  z c
i fala odbita prądu:
z odb  z c
io 
ip
z odb  z c
Tłumienność odbicia jest:
z odb  z c
  20 log
z odb  z c

Stan dopasowania falowego
zodb=zc
Nie występuje odbicie tak prąd jak i napięcia, czyli:
uo=0 oraz io=0
Linia nieobciążona – stan jałowy linii
zodb=∞
Współczynnik refrakcji (odbicia) R 
z odb  z c
1
z odb  z c
czyli odbita fala napięcia prądu i napięcia ma identyczną
amplitudę jak fala padająca uo=up oraz io=ip
Fala padająca napięcie
Sytuacja po odbiciu napięcie
Stan zwarcia
zodb=0
Współczynnik odbicia w przypadku zwarcia jest:
z odb  z c
R
 1
z odb  z c
co oznacza, że napięcie i prąd odbijają się z przeciwnym
znakiem, czyli przy zwarciu nastąpi:
u  up  uo
i  ip  io
zerowanie się wypadkowego napięcia i podwojenie wypadkowego
prądu
Dla uniknięcia odbicia stosuje się tłumiki dopasowujące.
Przykład tłumika dopasowującego dwa kable:
jeden o impedancji falowej 75Ω,
a drugi o impedancji falowej 50Ω
Z wej 
75  43.3  86.6
75  43.3  86.6
 50 z wyj
50  86.6
 43.3 
 75
50  86.6
Propagacja fal radiowych
Prędkość propagacji fal elektromagnetycznych w powietrzu:
1
c
 0 0
gdzie μ0=4π·10-7 H/m – przenikalność magnetyczna próżni,
ε0=8.8547·10-12 F/m – przenikalność elektryczna próżni,
stąd
c=3·108 m/s.
Widmo promieniowania elektromagnetycznego
c

f
Fale elektromagnetyczne rozchodzą się w postaci
fal poprzecznych (TEM)
Propagacja jonosferyczna
Zasięg pierwszego odbicia wyznaczamy:
θc – jest kątem krytycznym. Fale padające pod kątem mniejszym
od krytycznego nie zostaną odbite
Kąt krytyczny zależy od częstotliwości fal elektromagnetycznych,
ze wzrostem częstotliwości rośnie kąt krytyczny i fale są gorzej
odbijane przez jonosferę.
Częstotliwość fc, przy której kąt krytyczny jest równy zeru, jest
nazywana częstotliwością krytyczną
Maksymalną częstotliwość użytkową (MUF) wyznacza się z tzw.
prawa sekansa:
fc
MUF 
 fc sec c
cos c