Document

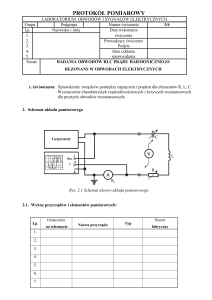
E3. ZJAWISKO REZONANSU W SZEREGOWYM OBWODZIE
PRĄDU PRZEMIENNEGO
tekst opracowała: Bożena Janowska-Dmoch
Gdy do obwodu zawierającego cewkę o indukcyjności L dołączymy naładowany kondensator
o pojemności C, to po zamknięciu obwodu zaobserwujemy zmiany natężenia prądu
1
powtarzające się periodycznie w czasie, czyli drgania. Częstość drgań  0 
, zwana
LC
także pulsacją, jest charakterystyczna dla danego obwodu i jest nazywana częstością drgań
własnych. Każdy rzeczywisty obwód ma skończony opór elektryczny R, na którym
dostarczona pierwotnie energia jest rozpraszana w postaci ciepła. Amplituda drgań zmniejsza
się w czasie i swobodne drgania elektryczne stopniowo zanikają. Są to tzw. drgania
tłumione. Częstość rezonansowa drgań tłumionych w obwodzie szeregowym RLC, wyraża
się wzorem:
2
r 
1  R
 R
     02   
LC  2 L 
 2L 
2
i jest mniejsza od częstości drgań własnych tego obwodu.
Aby wytworzyć w obwodzie drgania niegasnące należy stale doprowadzać do niego energię
równoważącą straty, co można osiągnąć np. przez włączenie do obwodu źródła sinusoidalnie
zmiennej siły elektromotorycznej. Drgania występujące wówczas w obwodzie nazywamy
drganiami wymuszonymi. Gdy przyłożone napięcie jest sinusoidalne, to prąd płynący przez
każdy z elementów obwodu jest również sinusoidalny, o częstości zgodnej z częstością zmian
siły elektromotorycznej, ale w ogólności przesunięty w fazie względem napięcia. Gdy
częstość źródła zbliża się do częstości drgań własnych obwodu amplituda natężenia prądu
gwałtownie wzrasta. Zjawisko to nosi nazwę rezonansu elektrycznego.
Obwody rezonansowe są stosowane jako obwody odbiorcze w radioodbiornikach, stosuje się
je również w generatorach drgań elektrycznych, generatorach ultradźwięków, rezonansowych
wzmacniaczach wielkiej mocy, lampach mikrofalowych i stabilizatorach częstotliwości.
Cel
Celem ćwiczenia jest:
 wyznaczenie krzywych rezonansowych poprzez pomiary charakterystyk
częstotliwościowych w szeregowym obwodzie RLC;
 zbadanie zależności częstotliwości rezonansowych i współczynnika dobroci od oporu.
Wymagania
Prąd elektryczny zmienny sinusoidalnie: siła elektromotoryczna, potencjał, napięcie,
natężenie, opór omowy, indukcyjny i pojemnościowy, zawada, częstość i częstotliwość.
Prawo Ohma i prawa Kirchhoffa. Prawo indukcji Faradaya, SEM indukcji. Szeregowe
obwody RLC zasilane napięciem zmiennym sinusoidalnie. Drgania elektryczne swobodne,
tłumione i wymuszone, zjawisko rezonansu. Dobroć układu rezonansowego.
2
Literatura
D. Halliday, R. Resnick, Fizyka, tom II, PWN
E.M. Purcell, Elektryczność i magnetyzm, Kurs berkelejowski tom II,PWN.
D. Halliday, R. Resnick, J. Walker, Podstawy fizyki, tom III, PWN
S. Szczeniowski, Fizyka doświadczalna cz. III, PWN.
K. Zboiński, Laboratorium z fizyki, Liber.
Opis układu
Na stanowisku pomiarowym
R
L
do kanału 2
mamy do dyspozycji następujące
przyrządy: generator funkcyjny
MX2020
firmy
Maxcom,
do kanału 1
Osc.
dzielnik
napięcia
DNa-18,
C
zasilacz 10V, opornik dekadowy
DR6, kondensator dekadowy
G
DK5, indukcyjność dekadowa
Z
DN
LD1, dwukanałowy oscyloskop
cyfrowy
TDS210
firmy
Schemat szeregowego obwodu RLC
Tektronix, płytka montażowa.
Przyrządy te należy połączyć, wykorzystując płytkę montażową, w szeregowy obwód RLC
według schematu przedstawionego na rysunku. Oznaczenia na schemacie: R – opór (opornik
dekadowy), L - indukcyjność (indukcyjność dekadowa), C – pojemność (kondensator
dekadowy), G – generator funkcyjny, Z – zasilacz prądu zmiennego, DN – dzielnik napięcia,
Osc - oscyloskop.
Źródłem siły elektromotorycznej o zmiennej częstotliwości jest generator funkcyjny G o
regulowanym napięciu wyjściowym i niskiej oporności wyjściowej ok. 50. Precyzyjną
regulację częstotliwości sygnału otrzymywanego na wyjściu generatora umożliwia specjalne
gniazdo, umieszczone na jego płycie czołowej oznaczone symbolem VCF IN, do którego
doprowadzony jest, regulowany dzielnikiem DN, sygnał napięciowy z zasilacza Z. Do
gniazda kanału 1 oscyloskopu należy doprowadzić napięcie zbierane na wyjściu generatora, a
do kanału 2 napięcie zbierane z kondensatora przez sondę oporową, która dzieli napięcie w
stosunku 1:10. Na ekranie oscyloskopu można wówczas obserwować oba przebiegi, jak
również odczytać amplitudy obu sygnałów i wartości skuteczne napięć.
Wyprowadzenie wzorów
Rozważmy obwód szeregowy, złożony z opornika R, cewki indukcyjnej L i kondensatora C
 0 cos  t . Korzystając z II
zasilany zmienną sinusoidalnie siłą elektromotoryczną
prawa Kirchhoffa zapiszemy zmiany napięcia w tym obwodzie:
 
U R U L UC 
RI  L
dI q
 
dt C

0

cos  t
3
ponieważ natężenie prądu I 
można zapisać w postaci:
dq
dI d 2 q
, a pochodna prądu
to powyższe równanie

dt
dt dt 2

d 2 q R dq

  02 q  0 cos  t
2
L dt
L
dt
(1)
1
gdzie  0 
jest częstością drgań własnych układu. Otrzymaliśmy równanie
LC
różniczkowe drugiego stopnia opisujące zmiany ładunku w obwodzie w dowolnej chwili
czasu. Rozwiązania tego równania poszukiwać będziemy jako funkcji periodycznej w czasie
zmieniającej się z tą samą częstością  co wymuszająca te zmiany siła elektromotoryczna
q  q0 cos t    .
Aby wyrażenie to stało się rozwiązaniem równania różniczkowego musimy wyznaczyć
wartości stałych – amplitudy ładunku q0 i przesunięcia fazowego  ładunku względem
napięcia.
Obliczamy pochodne ładunku po czasie
dq
  q 0 sin  t   
dt
d 2q
  2 q0 cos t   
2
dt
oraz
i wstawiamy do równania (1). Pamiętając, że  02 


q0  02   2 cos t    
1
, otrzymujemy
LC

R
 q0 sin  t     0 cos  t .
L
L
Stosujemy wzory na cosinus i sinus różnicy kątów i po przekształceniach otrzymujemy
równanie





R
R




cos  t q0  02   2 cos   q0 sin   0   sin  t  q0  02   2 sin    q0 cos  ,
L
L
L



które musi być spełnione w dowolnej chwili czasu. Aby tak się stało muszą jednocześnie
znikać wyrazy przy funkcjach cos  t i sin t

R

2
2
0
q 0  0   cos  L  q 0 sin   L  0

  02   2 sin   R  cos  0


L




tg  
R
L  02   2


Przesunięcie fazowe  zależy od częstości napięcia wymuszającego i w szczególnym
przypadku, gdy    0 przesunięcie w fazie między zmianami ładunku i siły

elektromotorycznej osiąga wartość   .
2
4
Z drugiego równania i z jedynki trygonometrycznej



2
R2 2
 cos 2    02   2 sin 2    02   2
2
L
a stąd
cos 


2
0
2
0

 2

2 2

  
2
2
0
 2
, co pozwala obliczyć sin  
R2
 2 2
L

2
cos 2 
R

L

2
0
 2
  RL
2
2
2
2
Wyznaczone funkcje trygonometryczne wstawiamy do pierwszego równania i otrzymujemy
wyrażenie na amplitudę ładunku

2

02   2

q0

2

2
R
2
 0   2  2  2
L







q0 



 0
2

L
2
R
 2  2  2 
L

R2 2

L2
L 0  
2
2
0

0

2 2

R2
 2 2
L
.
Amplituda ładunku na kondensatorze jest funkcją częstości napięcia wymuszającego q0().
q
Badając tę funkcję znajdziemy maksymalną wartość amplitudy ładunku z warunku 0  0

3



q0
R 2 2  2 
R 2 
2
2 2
2
2
0  1


   0  
  2  0    2   2 2     0

L  2
L2 
L 








Równanie to będzie spełnione, gdy częstość drgań będzie równa:
 r   02 

R2
, a maksymalna amplituda q0 max  0
R
2L2
1
R2
 02  2
4L
.
W takim przypadku, gdy amplituda drgań ładunku osiąga wartość maksymalną w
obwodzie występuje zjawisko rezonansu, a częstość drgań r, dla której zachodzi
rezonans nazywamy częstością rezonansową.
Zmieniającemu się w czasie ładunkowi przepływającemu w obwodzie RLC towarzyszą
zmiany napięcia na kondensatorze
UC 

q q0
 cos t     0
C C
LC
1

2
0


2 2
R2 2
 2
L
cos t     U C 0 cos t    ,
5
gdzie amplituda napięcia
U C0 

0

2
0
 2

2
UC0
2
0

R 2 2
L2
R1
. (2)
R2
W rezonansie amplituda napięcia
na kondensatorze staje się
maksymalna:

U C 0 max 
CR  02 
przy  r   02 
R3
0
R4
2
R
4L2
R2
2L2
r3 r1
r4 r2
0

Wartość amplitudy napięcia, podobnie jak częstości rezonansowej, maleje wraz ze wzrostem
oporu omowego obwodu. Zauważmy, że gdy   0 , to U C 0  0 , zaś gdy    , to
U C 0  0 .Wykres zależności U C 0   nazywamy krzywą rezonansową. Na powyższym
wykresie przedstawiono krzywe rezonansowe dla szeregowego obwodu RLC dla różnych
wartości oporu omowego R1<R2<R3<R4 (L i C – stałe). Im mniejszy jest opór tym większa
jest wartość amplitudy napięcia U C 0 i krzywa rezonansowa ma bardziej stromy przebieg.
Wielkością charakteryzującą rezonansowe własności obwodu drgającego jest współczynnik
dobroci Q. Dobroć jest proporcjonalna do stosunku całkowitej energii drgań E,
zmagazynowanej w obwodzie w warunkach rezonansu, oraz energii straconej w czasie
jednego okresu Es
E
Q  2
.
Es

Energia nagromadzona w obwodzie RLC jest maksymalna dla częstości    0 i jest równa
sumie energii pola elektrycznego w kondensatorze EC i pola magnetycznego w cewce EL
2
E  EC  E L 

1 2 1 2
1 2 1  dq 
q  LI 
q  L  
2C
2
2C
2  dt 

2
1 2
1
1 q02 1
q0 cos 2  0 t     Lq02 02 sin 2  0 t    
 L 02
2C
2
2 C 2 R
Zauważmy, że energia całkowita jest wielkością stałą.
Energia stracona w czasie jednego okresu jest równa pracy wykonanej w tym czasie przez
źródło siły elektromotorycznej przy przepływie prądu przez opornik. Energia ta rozprasza się
jako ciepło Joule’a
T
2 T
2
1 02
Es  
dt  0  cos 2  0 t dt 
T.
R
R
2
R
0
0



6
Zatem dobroć obwodu
Q  2
Q

2
1
2R
2 L
L 02 2 
2 R
T R
0T
r L
R


1
 r CR
(3)
jest tym większa im mniejszy jest opór omowy obwodu. Przy niewielkim tłumieniu
1 L
.
Q
R C
Jedna z metod wyznaczenia współczynnika dobroci układu wynika z rozważań zmian mocy w
obwodzie RLC w funkcji częstości . Średnia moc jest dana wyrażeniem:

2
1
1
1
1
 dq 
P   RI 2 dt   R  dt  R 2 q02  R 2
T 0
T 0  dt 
2
2
T
T
2
0


2
R2
L  02   2   2  2 
L


Zależność średniej mocy od częstości przedstawia poniższy wykres:

.
2
P
2
0
2R


2
0
4R
0
1
0

2

Dla    0 średnia moc jest maksymalna i wynosi P 


połowy, czyli była równa P
2
0
4R
2
0
2R
. Aby średnia moc spadła do
, częstość musi być mniejsza od  0 i wynosić 1 takie,
że
P 

2
0
4R
gdy
R2 2
1
L2

2
0

 12
2

2
R
12
L2

1

2

2
0
 12

2

R2 2
1
L2
  02  12 
Analogicznie dla częstości  2 większej od  0

2
0
  22

2

R2 2
2
L2
R
  02   22    2 , bo  2   0
L
R
1
L
7
Odejmując otrzymane równania stronami otrzymamy
R
 22  12  1   2 

L
a ponieważ Q 
r L
R
 2  1   
R
L
, to
Q
r

lub Q  r .


(4)
Współczynnik dobroci jest równy stosunkowi częstości rezonansowej obwodu  r do
szerokości    2  1 krzywej rezonansowej P  na wysokości odpowiadającej
połowie mocy. Różnica częstotliwości  jest nazywana pasmem przenoszenia.
W praktyce, ponieważ moc jest proporcjonalna do kwadratu napięcia P ~ U C2 , to
dobroć wyznaczamy z krzywej rezonansowej U C   mierząc jej szerokość na wysokości
U C0
amplitudy w stanie rezonansu.
2
Inna, wygodna metoda wyznaczania współczynnika dobroci obwodu RLC jest oparta o prawo
Ohma dla prądu zmiennego, z którego wynika, że amplituda napięcia na kondensatorze jest
1
wprost proporcjonalna do amplitudy natężenia prądu, czyli U C 0  X C I 0 , gdzie X C 
C
jest oporem pojemnościowym (reaktancją pojemnościową). W stanie rezonansu I 0 
czyli U C 0 
1
 r CR

0

0
R
,
. Korzystając z równania oznaczonego (3) zapiszemy
U C0

0

1
Q
 r CR
lub
Q
U Csk

.
(5)
sk
Współczynnik dobroci jest równy stosunkowi amplitudy napięcia na kondensatorze U C 0
w warunkach rezonansu (lub wartości skutecznej U Csk tego napięcia) do amplitudy napięcia
generatora

0
(lub napięcia skutecznego

sk).
Wykonanie ćwiczenia
Wyniki wszystkich pomiarów muszą być zapisane w sprawozdaniu, opatrzone odpowiednimi
jednostkami i podpisane przez asystenta.
Uwyj
a) Na płytce montażowej łączymy kablami
opornicę dekadową z dekadami indukcyjności i
L
C
pojemności w szeregowy obwód RLC. Napięcie
zbierane z generatora jest podane na kanał 1
oscyloskopu, a na kanał 2 jest podane napięcie
wyjściowe z kondensatora poprzez sondę
oporową osłabiającą sygnał w stosunku 1:10.

8
Krzywe rezonansowe:
b) Wybieramy pojemność z przedziału 1nF 100 nF i indukcyjność z przedziału
40 mH  1H i ustawiamy odpowiednie wartości na dekadach. Obliczamy częstość i
częstotliwość własną obwodu. Na oporniku dekadowym ustawiamy R = 0. Należy
jednak pamiętać, że na opór omowy układu Ru składają się: opór RG, którym zwarty
jest generator, opór omowy włączonej dekady cewek indukcyjnych RL i opór
włączony na oporniku dekadowym R, czyli
Ru  RG  RL  R ,
gdzie RG = 50 , zaś RL dla różnych wartości indukcyjności są podane w poniższej
tabeli
L
[mH]
RL
[]
100
200
300
400
500
600
700
800
900
1000
207
294
364
431
485
532
584
627
668
712
c) Po sprawdzeniu obwodu przez asystenta i włączeniu zasilania na ekranie oscyloskopu
są widoczne dwa sygnały – z kanału 1 sygnał generatora, a z kanału 2 sygnał zebrany
z kondensatora. Przy wciśniętym klawiszu MEASURE na ekranie są wyświetlane dla
każdego kanału wartości skuteczne napięcia (oznaczone Cyc RMS). Możliwe są
także pomiary częstotliwości (Freq), podwojonej amplitudy (Pk-Pk), okresu (Period) i
średniej arytmetycznej napięcia w czasie całego pomiaru (Mean).
d) Napięcie skuteczne sygnału z generatora powinno wynosić około 6 V.
e) Zmieniając częstotliwość sygnału z generatora poszukujemy częstotliwości
rezonansowej w okolicy obliczonej częstotliwości własnej obwodu. Częstotliwość,
przy której napięcie na kondensatorze osiągnie wartość maksymalną jest
częstotliwością rezonansową (odczytujemy ją na generatorze). Notujemy wartości
UCmax i r.
f) Następnie odstrajamy stopniowo układ od rezonansu tak, by kolejna zmiana
częstotliwości (np. zmniejszenie) powodowała spadek napięcia UC o około 3  5%
U
poprzedniej wartości aż do napięcia C max . Dalsze zmiany częstotliwości powinny
2
powodować większe spadki napięcia UC o około 10  15% . Pomiary kontynuujemy
do napięcia około ¼ UCmax.
9
g) Dla tych samych wartości napięcia UC, jak w punkcie e), mierzymy częstotliwości
odstrajając układ od rezonansu w przeciwną stronę (np. zwiększając częstotliwość).
h) Przerywając na czas odczytu połączenie obwodu rezonansowego mierzymy na
kanale 1 skuteczną wartość napięcia

sk
dla generatora nieobciążonego.
Propozycja zapisu wyników:
Ru = ............. , R = .............
L= ............ , L = ............. C = ............. , C = ...............
Częstotliwość własna: 0 = ............,
Częstotliwość  < r
[jednostka]
 = ......

sk
= ..................
Częstotliwość  > r
[ jednostka]
Napięcie UC
[jednostka]
UC = ......
gdzie , R, L, C są błędami systematycznymi wynikającymi z dokładności (klasy)
przyrządów.
i) Analogiczne pomiary, jak w punktach d)  f), wykonujemy ustawiając na oporniku
dekadowym najpierw opór R = 200 , a następnie 400 , gdy 0 < 2 kHz, dla
większych częstotliwości ustawiamy 500 , a następnie 1000 ,
Współczynnik dobroci:
j) Dla tych samych wartości indukcyjności i pojemności wykonujemy serię pomiarów
notując częstotliwości rezonansowe r, napięcia UCmax i częstotliwości na poziomie
U
U C  C max po obu stronach, zmieniając opór R od zera do 1000 co 100, gdy
2
0 < 2 kHz, dla częstotliwości 2 kHz <0 <5 kHz zmieniamy opór co 200  od zera do
2000, dla 0 >5 kHz zmieniamy opór co 500  od zera do 5000.
Propozycja zapisu wyników:
L= ............ , L = ............. C = ............. , C = ...............
Częstotliwość własna: 0 = ............,

sk
= ..................
10
Opór Ru
Częstotliwość r Napięcie UC0
[jednostka] [jednostka]
[ jednostka]
R = ......
 r = ......
UC0 = ......
Częstotliwość 1 < r Częstotliwość 2 > r
[ jednostka]
[ jednostka]
 = ......
 = ......
gdzie , R, L, C są błędami systematycznymi wynikającymi z dokładności (klasy)
przyrządów.
k) Zmieniamy parametry układu tak, aby dobroć obwodu wzrosła i wykonujemy serię
pomiarów jak w punkcie k).
Opracowanie wyników
a) Na papierze milimetrowym wykreślamy we wspólnym układzie współrzędnych
rodzinę krzywych rezonansowych UC() dla różnych wartości oporu Ru, zaznaczając
dla każdej krzywej częstotliwość rezonansową. W kilku punktach zaznaczamy
niepewności pomiarowe. Wykresy można wykonać wykorzystując programy
komputerowe.
Dla chętnych korzystających z programów komputerowych – na tym samym
wykresie rysujemy krzywe rezonansowe UC() obliczone ze wzoru (2) po dobraniu
dla każdej z nich takiego stosunku R/L, aby najlepiej pasowały do krzywych
doświadczalnych. Wyznaczamy wartość oporu tłumiącego R.
U
b) Wyznaczamy szerokość krzywych rezonansowych na poziomie C max .
2
c) Obliczamy współczynnik dobroci obwodu Q dla różnych wartości oporu Ru
korzystając ze wzoru oznaczonego (4), jak również ze wzoru (5). Wyznaczamy
niepewności pomiarowe Q.
d) We wspólnym układzie współrzędnych wykreślamy zależność odwrotności
współczynnika dobroci 1/Q, obliczonego ze wzoru (4), jak również ze wzoru (5), w
funkcji oporu Ru. Metodą najmniejszych kwadratów (regresji liniowej) wyznaczamy
współczynniki A i B prostych najlepiej dopasowanych do punktów pomiarowych.
Nanosimy te proste na wykres. Wyznaczamy również niepewności pomiarowe A i
B.
1
e) Jeśli współczynnik B w metodzie
Q
regresji jest różny od zera, to oznacza,
że nie uwzględniliśmy jeszcze w
naszych rachunkach oporu zwanego
rozproszonym Rr. Brakujący opór
możemy
wyznaczyć
znajdując
przecięcie prostej wyznaczonej w
punkcie c) z osią Ru. Obliczamy
niepewność pomiarową Rr.
Rr
Ru
11
We wnioskach spróbujmy:



ocenić wpływ parametrów układu na przebieg zjawiska rezonansu;
porównać współczynniki dobroci obliczone ze wzorów (4) i (5);
porównać wartość oporu tłumiącego Ru+ Rr z oporem wyznaczonym w
punkcie a).